齒面粗糙度參數與接觸應力的敏感性分析研究

陳季凌, 唐進元, 楊鐸

(1.中南大學 機電工程學院, 湖南 長沙 410083; 2.中南大學 高性能復雜制造國家重點實驗室, 湖南 長沙 410083)

齒輪加工表面在微觀尺度上都是凹凸不平的表面,在傳動時齒面的微觀表面形貌特征直接影響著承載能力和磨損、疲勞等性能[1-2]。關于機械加工表面形貌特征的表征方面,三維粗糙度參數因其能更真實、準確地反映一定面積區域上的表面形貌特征,彌補了二維表面參數統計性差、信息片面性等不足,而受到重視,逐漸成為研究熱點[3]。眾多研究者基于三維粗糙度參數與加工面各項服役性能間關聯規律開展了大量研究[3-12]。何寶鳳等[3]認為參數Vmp值較大代表較好的承載能力,Vvv值較大代表較好的潤滑能力,參數Sa與參數Sq存在最強相關性。王金明等[4]從參數Sa定義深入探討,基于此建立了復合材料切削表面的測試方法,為評估其表面質量提供基礎。Stout等[5]利用參數Sa,Sq,Ssk,Sku探討軋制鋼板表面的織構轉移特性,并確定了轉移的程度。Bulaha[6]借助參數Sa,Str,Ssk,Smr1和Smr2評估了確定圓柱磨面的耐磨性。李伯奎等[7]通過實驗得出參數Ssk,Sku與不同加工面的摩擦磨損性能有重要的對應關系。Oskars等[8]首次在磨損估計公式中使用了Sa,Str等三維粗糙度參數。Civcisa等[9]利用三維粗糙度高度參數分析了不同材料表面的使用性能。趙仕宇等[10]利用功率譜和三維粗糙度參數Sq,Ssk,Sku,Sz和Str分析了影響成形件表面質量的相關因素。王棟等[11]通過實驗得出試樣疲勞壽命次數與三維粗糙度參數Sa,Sq,Sz,Ssk,Sku均有明顯的相關性。Franco等[12]指出參數Vmp,Vvv為磨損分析提供了重要信息。以上研究表明,使用三維粗糙度參數可以評估加工面的各項服役性能。

然而三維粗糙度參數眾多,從眾多參數中篩選出少部分代表性參數用于表征表面特定服役性能是一個難題。為剔除不必要的自變量,研究者常依據統計學線性相關分析理論剔除相關系數小于閾值的變量,從而實現自變量的初步篩選[13-14]。考慮到三維粗糙度參數與齒面接觸性能間可能存在非線性映射關系,采用遺傳算法優化的BP神經網絡(GA-BP)構建初步篩選的粗糙度參數與接觸性能參數預測模型。同時,為進一步對參數進行篩選,基于神經網絡模型,借助全局敏感性分析方法[15-17],剔除掉敏感系數小的參數,篩選出對齒面接觸性能影響最大的三維粗糙度參數。

本文基于超聲磨削加工表面形貌實測數據,以相關分析理論與全局敏感性分析方法為基礎,借助神經網絡構建三維粗糙度參數與輪齒接觸最大剪應力、表面最大壓力的非線性映射模型,探究三維粗糙度參數與齒面接觸性能參數間的關聯規律。同時對冗余的三維粗糙度參數進行降維,旨在尋找最為關鍵的少部分參數控制齒輪表面質量,并分析其影響齒面接觸性能的參數重要性,為齒面抗疲勞設計制造提供理論基礎。

1 數據獲取與計算

本研究所依據的數據來源于實測超聲磨削表面,針對實測表面展開接觸性能參數與三維粗糙度參數的計算。

1.1 粗糙表面數據獲取與接觸應力計算

對齒輪材料12CrNi4A(9 mm×9 mm×16 mm)進行超聲振動平面磨削,采用半徑為100 mm寬度為20 mm的CBN砂輪(120目)進行加工。加工條件為：砂輪轉速1 500 r/min,切削速度200 mm/min,切削深度5～25 μm,冷卻液120 L/min(Castrol Syntilo 2000)。超聲振動采用橫向進給方式,頻率為20 kHz,振幅為0～10 μm。

使用白光干涉儀Wyko NT9100對磨削工件表面形貌進行測量,獲得工件表面微觀形貌的高度矩陣數據Z(x,y)(共228組)。所使用的白光干涉儀采集工件表面形貌的放大倍率為5倍,儀器鏡頭的整個采集過程始終垂直于工件表面。基于Wen等[18]提出的三維粗糙表面微凸體建模與接觸分析方法,并借助彈性半空間理論和接觸力學理論求解在齒面壓力和剪切力作用下產生的次表面應力場,計算出最大剪應力(τ)與表面最大壓力(MP),其中應力單位為MPa。

1.2 三維粗糙度參數選用與計算

依據ISO25178中規定的三維粗糙度參數,對超聲磨削試驗采集表面微觀形貌數據進行計算。基于相關文獻[3-12]初步篩選出對加工表面接觸性能影響較大的表征參數作為目標參數,包括算術平均高度(Sa)、最大峰高和最大谷深的和(Sz)、偏斜度(Ssk)、峰態(Sku)、谷部的空隙容積(Vvv)、峰部的實體體積(Vmp)、紋理特征比(Str)、分離突出峰部與中心部的負載面積率(Smr1)、分離突出谷部與中心部的負載面積率(Smr2)共9個三維粗糙度參數。其中除Smr1,Smr2外的三維粗糙度參數的數學表達式如表1所示,關于Smr1,Smr2的計算方法如圖1所示。

表1 三維粗糙度參數的數學表達式

圖1 取樣區域的Abbott曲線圖

2 預測模型構建與全局敏感性分析

本研究采用統計學相關分析理論初步對三維粗糙度參數進行初步篩選,借助BP神經網絡搭建三維粗糙度參數與接觸性能參數的預測模型。基于預測模型,應用全局敏感性分析方法計算出各個三維粗糙度參數的敏感度并進一步篩選參數。

2.1 相關分析

相關分析常用于研究2個或2個以上不同變量間的種種相關特性和緊密程度[13]。對數據展開相關分析首先須通過顯著性檢驗,若顯著性p值小于0.05,即可認為此差異具有統計學意義[19],即對結果真實程度的一種估計方式,p值越小,表明結果越顯著。其次劃分相關程度,皮爾遜相關系數(Pearson correlation coefficient)因其能從線性相關角度定量描述兩變量間的相關趨勢,故常用作判別指標。因本文所使用的數據均為連續變量,此處運用皮爾遜相關系數分別探究三維粗糙度參數與接觸性能參數的關聯程度。計算公式為

(1)

式中,ri,j是變量i,j間的皮爾遜相關系數,分子為兩變量間的協方差,分母為各變量的方差。表2中所列出的皮爾遜相關系數r值范圍,常用于衡量兩變量間的相關程度。

表2 相關程度判定表

2.2 GA-BP網絡預測模型

本文借助相關分析去除掉弱相關程度的三維粗糙度參數,剩余的參數與齒面接觸性能參數既包含線性關系又包含非線性關系,且在利用全局敏感性分析前需要建立一個穩定的映射模型,故采用BP神經網絡擬合模型。傳統的BP神經網絡存在一些缺陷:缺少對冗余參數(輸入參數)的有效篩選、易產生過擬合、易陷入局部最優解[20]等。

遺傳算法(genetic algorithm)是一種用于解決最佳化的搜索算法,它具備全局尋優的能力,用于更新BP神經網絡的初始權值。GA算法包括:種群初始化、適應度函數、選擇操作、交叉操作、變異操作[21]。

種群個體的初始化是對初始值進行編碼,一般采用實數編碼,編碼包括網絡的權值與閾值。據BP神經網絡的誤差計算得到,如(2)式所示

(2)

式中：c為常數；R為神經網絡中的節點數；Ki為神經網絡的輸出數；Li為期望數值。

選擇操作、交叉操作和變異操作是為了在神經網絡中產生新的權值與閾值,滿足適應度值的要求即將新的權值與閾值賦予BP網絡,進而使得網絡具有全局尋優的功能。遺傳算法彌補了BP神經網絡易陷入局部最優的不足,提高了神經網絡的準確性與穩定性,但由于輸入的三維粗糙度參數的冗余將導致預測結果不穩定,因此本文提出一種結合統計學相關分析與全局敏感性分析的篩選方法,并基于GA-BP神經網絡對接觸性能參數進行預測。

2.3 全局敏感性分析方法

本文使用了2種被廣泛應用的全局敏感性分析方法:Morris[15]方法和Sobol′[16]方法。Morris方法可以基于少量樣本定性確認相對重要參數,而Sobol′方法可基于較多樣本對參數做定量敏感性分析。通過對比2種方法的敏感性分析結果,為三維粗糙度參數篩選提供合理依據。

2.3.1 Morris方法

為了能在全局范圍內研究模型參數的敏感性,Morris在1991年提出了Morris方法。該方法每次僅改變一個參數的取值,依次計算得出各個參數“基本影響”,進而得到模型中輸入參數對輸出結果的影響,以較小的計算代價得出參數全局靈敏度的比較及參數相關性和非線性的定性描述[16]。

設系統模型為y=f(x1,x2,…,xm),m表示參數的維度,依據Morris的抽樣準則,將各參數值映射至[0,1]區域內,使各參數從集合M={0,1/(k-1),2/(k-1),…,1}內取值,其中k為各參數的水平數,每個參數從M中隨機取值獲得第一個樣本點X0=(x1,x2,…,xm),對X0的任意一個參數xi增加擾動s即可得到樣本點X1=(x1,…,xi+s,…,xm),其中s為1/(k-1)的整數倍,樣本點X2基于X1對非xi參數增加擾動,以此類推直至遍歷所有參數,得到一組樣本點集{X0,X1,…,XM}。由相鄰2組的樣本點即可計算出各參數對輸出結果的作用值,第q個參數的作用值可用公式(3)計算

(3)

式中，Xq=(x1,…,xq+s,…,xm),Xq-1=(x1,…,xq,…,xm)。

一組樣本集僅代表對模型的局部敏感性分析,將獲得樣本點集的過程重復n次,即可代表整個樣本空間,假定某個參數xi服從分布N,即可計算得到均值μi,其中μi值用于衡量對系統輸出值的影響,μi值越大,影響程度越大,反之則小,進而可確定xi的全局敏感性。

2.3.2 Sobol′方法

Sobol′方法是一種基于方差分解的敏感性分析方法,它可以有效解出高度非線性模型中參數間相互作用產生的靈敏度,計算結果穩定可靠。

假定模型為Y=F(x)=f(x1,x2,…,xM),且f(x)的平方可積,其中M為參數維度,可把模型分解成如下形式

(4)

式中，F0為常數項,i=1,2,…,n,若xi～U(0,1),其中U為均勻分布,則模型F(x)方差分解形式唯一,其分解結果如下

(5)

式中：V表示總方差,Vi與Vij分別表示單雙因子方差,以此類推,V1,2,…,n為n個因子方差。化簡后得到

(6)

式中：Si=Vi/V,反映xi為一階主效應的敏感度；Sij反映xi與xj中二階交互效應的敏感度,以此類推。將包含xi的敏感度累加,即可得到xi的總效應敏感度Sxi。

3 研究結果與分析

3.1 技術路線

為合理地篩選出與齒面接觸性能參數間敏感性較大的三維粗糙度參數,制定圖2所示的技術路線。

圖2 關聯規律探究技術路線圖

1) 依據相關分析理論,從統計學角度對三維粗糙度參數與接觸性能參數進行顯著性檢驗并計算對應的相關系數,利用皮爾遜相關系數閾值初步篩選參數并對篩選結果進行參數重要性排序。

2) 為減少模型復雜度,利用GA-BP模型(遺傳算法優化的BP神經網絡)分別構建三維粗糙度參數與最大剪應力(τ)、表面最大壓力(MP)間的預測模型。

3) 基于GA-BP神經網絡模型,分別應用Morris方法與Sobol′方法對參與擬合模型的三維粗糙度參數進行全局敏感性分析,對比2種方法的分析結果,從定性、定量分析角度對三維粗糙度參數進一步篩選。

4) 將篩選后的參數重新放入GA-BP模型中,再次利用2種全局敏感性分析方法對參數重要性進行排序,將排序結果與步驟3)結果進行比較,并將對比結果與相關分析排序結果進行交叉驗證,得到最終的三維粗糙度參數重要性排序結果。

5) 為探討上述參數篩選過程的有效性,將參數篩選前后的神經網絡模型進行對比,驗證其有效性。

3.2 相關分析結果

三維粗糙度參數與齒面接觸性能參數的相關分析結果如圖3所示。根據表2的相關程度劃分選取相關程度大于0.3且接近0.3的中等及以上相關程度的三維粗糙度參數,其中篩選出的參數均通過顯著性檢驗。

圖3 三維粗糙度參數與接觸性能參數間的相關分析

從圖3可以看出,與輪齒接觸最大剪應力、表面最大壓力呈現中等相關程度及以上的粗糙度參數依次為:Sz,Sa,Vvv,Vmp,按照相關程度由大到小排序依次為:Sa,Vmp,Vvv,Sz。這4個參數對最大剪應力與表面最大壓力均起到正向促進作用,其中Sa均達到強相關程度。

通過顯著性p值檢驗與統計學相關分析篩選出:Sa(算術平均高度),Sz(取樣區域中最大峰高和最大谷深的和)，Vmp(峰部的實體體積)，Vvv(谷部的空隙容積)作為模型原始輸入變量。為簡化模型,將τ(最大剪應力)與MP(表面最大壓力)依次作為GA-BP網絡的輸出變量。利用Matlab搭建神經網絡模型,從228組超聲磨削加工表面實測數據中隨機抽樣228×0.8≈182組數據用于訓練神經網絡模型,GA-BP模型自動將其按照3∶1∶1的比例劃分為訓練集、驗證集與測試集，剩余46組數據作為測試集。基于訓練后的映射模型對輸入變量的參數重要性進行全局敏感性分析。

3.3 全局敏感性分析結果

對參數進行敏感性分析的主要研究工具為軟件包SALib,SALib是由Python編寫并用于執行敏感性分析的開源庫,其中包括了本研究所涉及的全局敏感性分析方法。

由于輸入樣本的不均勻性,直接基于實測樣本進行全局敏感性分析可能會導致分析結果出現誤差,故將神經網絡訓練后的映射模型提取出來,基于映射模型生成均勻樣本并進行全局敏感性分析。根據文獻[15],Morris方法所需樣本量為n+1的整數倍,其中n為參數的個數,為探索得到合理結果的最佳樣本量,分別設置樣本量為10,30和50。同時,為驗證Morris定性分析結果的可靠性,本研究采用Sobol′敏感性分析方法,生成1 000個樣本對4個粗糙度參數做定量分析。對三維粗糙度參數重要性的定性、定量結果分析如圖4所示,其中均值μ與總效應敏感度S越大,表明它對接觸性能參數的影響越大。

基于BP模型,由軟件包SALib運用Morris法與Sobol′法分別計算得到各參數的均值與總效應敏感度S,得到圖4結果。由圖4的定性定量分析結果可以直觀得到,在預測最大剪應力與表面最大壓力的神經網絡模型中,參數Vvv,Sz的2種敏感性分析結果均遠低于其他參數值。由此得到最終的參數篩選結果:參數Sa,Vmp作為預測輪齒接觸最大剪應力、表面最大壓力的輸入變量,參數Vvv,Sz剔除。

圖4 全局敏感性分析結果一

為合理評估粗糙度參數重要性排序結果,保留神經網絡的拓撲結構,僅變動模型的輸入輸出參數,將剔除變量后的三維粗糙度參數(Sa,Vmp)作為神經網絡的輸入變量,基于實測樣本重新訓練網絡,并將訓練好的神經網絡映射模型再次提取出來,重新生成均勻樣本并進行全局敏感性分析。為與參數篩選前的樣本量選用方法保持一致,分別設置Morris法的樣本量為6,18和30,Sobol′法的樣本量為1 000。全局敏感性分析結果如圖5所示,神經網絡訓練的迭代過程如圖6所示。

對比圖5與圖4結果,可見剔除參數后的三維粗糙度參數敏感性分析排序結果與剔除前排序一致;對比圖5與圖3結果,2種敏感性分析結果與相關分析結果排序仍然保持一致。2種對比結果最終得出一致結論,即通過統計學相關分析與全局敏感性分析的參數篩選后,影響輪齒接觸最大剪應力、表面最大壓力的三維粗糙度參數重要性排序均為:Sa>Vmp。對Sa,Vmp進行相關分析,二者的皮爾遜相關系數為0.653,為中等相關強度。雖然兩參數存在一定的相關性,依據相關文獻[4-6,8-11]可以看出Sa的重要地位及其廣泛性的應用。此外,文獻[12]提出參數Vmp為磨損分析提供了重要信息,文獻[3]提出Vmp值較大代表較好的承載能力。由此可以得出篩選結果與各文獻中的結果相對應,故保留參數Sa,Vmp。

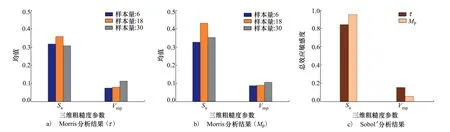
圖5 全局敏感性分析結果二

圖6 3種不同網絡的綜合表現

4 GA-BP神經網絡穩定性分析

上述研究利用統計學相關分析理論與全局敏感性分析方法對三維粗糙度進行降維且得出,算術平均高度(Sa)、峰部的實體體積(Vmp)作為預測輪齒接觸最大剪應力(τ)、表面最大壓力(MP)的關鍵參數。然而參數降維后GA-BP神經網絡的穩定性是否可靠,需對其進一步驗證。

4.1 穩定性分析

為深入探討相關分析與全局敏感性分析篩選參數前后對模型穩定性的影響,不更改神經網絡的隱含層層數、隱含層神經元個數以及網絡訓練學習率等相關參數,僅變動神經網絡的輸入參數,基于上述參數篩選過程展開對比分析。即對未篩選參數的GA-BP模型、相關分析篩選參數后的GA-BP模型(P-GA-BP)、相關分析與全局敏感性分析篩選參數后的GA-BP模型(P-Morris/Sobol′-GA-BP)進行訓練,圖6為各模型的訓練迭代過程。

根據預測數據,計算均方誤差(MSE)與平均絕對百分比誤差(MAPE)可以評價數據的變化程度,MSE值越小,說明預測模型描述實驗數據具有更好的精確度,MAPE值越小,模型誤差越小。均方誤差與平均絕對百分誤差的計算如(7)～(8)式所示。

式中:M為數據數量;ym′為第m個數據的預測值;ym為第m個數據的真實值。

(7)～(8)式計算的對比結果如表3所示,可以看出P-Morris/Sobol′-GA-BP模型的EMS與EMAP值略低于GA-BP神經網絡,可見前者模型穩定性略高于后者,也從側面進一步證實了參數篩選的有效性。

表3 測試集均方誤差與平均絕對百分誤差對照表

4.2 結果分析

由表3與圖6可直觀看出,對比未進行參數篩選的預測模型,利用相關分析與全局敏感性分析對三維粗糙度參數進行篩選的預測結果(EMS、EMAP)相對偏小,且在BP網絡迭代過程中不易出現過擬合。這是因為未進行參數篩選的BP模型輸入變量過多,造成了輸入變量的冗余,致使網絡不穩定。而經參數篩選后縮減了無關變量的輸入,提高了網絡預測的穩定性,進而減小預測誤差。

5 結 論

本文基于實測超聲磨削微觀表面數據,探究三維粗糙度參數影響齒面接觸性能參數的主次關系,并對其進行降維,得到了以下結論:

1) 皮爾遜顯著性檢驗與相關分析結果表明:與輪齒接觸最大剪應力(τ)、表面最大壓力(MP)呈現中等相關及以上的三維粗糙度參數按照相關程度大小排序依次為:Sa,Vmp,Vvv,Sz,均起到正向促進作用。其中參數Sa與接觸性能參數的相關系數最大,達到強相關程度。

2) 利用Morris和Sobol′方法對三維粗糙度參數敏感性進行定性與定量分析并得到一致結果,影響輪齒接觸最大剪應力、表面最大壓力的參數重要性從大到小依次排序為Sa,Vmp。故在實際工程中評判齒面接觸性能參數時,更要關注Sa,Vmp這2個參數。

3) 穩定性分析結果表明,基于相關分析與全局敏感度分析篩選參數后訓練的GA-BP模型在穩定性上略高于未篩選參數訓練的GA-BP模型,實現了三維粗糙度參數降維,也進一步驗證了參數篩選的有效性。