基于MCMC方法的區間控制偽裝缺失值檢測算法

史金余 孫禹明 謝 兄 劉衛江 滕俊凱

(大連海事大學大學信息科學技術學院 遼寧 大連 116026)

0 引 言

在大數據應用快速發展的今日，臟數據漸漸地成為數據分析的一大障礙，不僅會誤導我們的工作行為，還可能造成巨大的經濟損失。為了減少臟數據帶來的嚴重影響，數據清洗在數據處理的過程中起著越來越重要的作用。數據清洗[1]是一個檢測、診斷和編輯臟數據的過程。近幾年研究表明，在進行數據清洗時，離群點檢測技術成為了一種被廣泛應用的數據識別技術，如工業損傷檢測[2]、網絡入侵檢測[3]、欺詐檢測[4]、臨床醫學檢測[5]和地質探測[6]等。

為了提高檢測效率，現在很多研究都對離群點進行了分類[7]，在所有類中，對偽裝缺失值的檢測成為了一個難題，尤其是在數據范圍內隨機分布并在數據集中經常使用的有效值(以下簡稱有效值類偽裝缺失值)。因此在本文主要講解數據集中有效值類偽裝缺失值的檢測方法，目前已有很多學者采用了不同的方法對偽裝缺失值檢測問題進行了相關研究。Hua等[8-9]提出了DiMaC算法，該算法提出了一種嵌入式無偏樣本啟發式算法來檢測偽裝缺失值；Pit-Claudel等[10]提出了dBoost算法，該算法利用元組擴展來檢測各種數據集中的離群點；Qahtan等[11]提出了FAHES算法，該算法主要是將偽裝缺失值分成outlier和inlier兩類采用不同的方法進行檢測。三種算法中，dBoost算法并非主要檢測偽裝缺失值，因檢測范圍過大，會檢測到非偽裝缺失值，而DiMaC算法解決了此問題，但其運行時間較長。FAHES算法進行了分類檢測也縮短了運行時間，但由于分類不夠細致，仍然會有很多種類的錯誤出現在分類之外。對上述三種算法的研究發現，其檢測效果不好的主要原因在于檢測范圍問題。為了提高檢測效率，本文提出一種基于MCMC方法的區間控制偽裝缺失值檢測算法，來解決檢測范圍帶來的麻煩。

在龐大的數據集中，為了在進行數據分析時取得良好的結果，非常有必要進行偽裝缺失值檢測，而本文算法主要采用MCMC算法和基于統計學的離群點檢測算法，如果想有效地使用兩種算法將面臨如下挑戰：

(1) 在檢測中使用對基于統計學的離群點檢測算法的改進來確定控制區間進行檢測，但數據集中存在異常點，這必然會導致數據集的相關參數的變化，直接使用這些參數必然會產生一些誤差，因此需要解決如何減少參數引起的誤差問題。

(2) 從檢測范圍的角度來提高檢測效率，主要通過縮小檢測范圍來提高檢測效率，因此需要解決如何聚焦檢測范圍的問題。

本文主要貢獻是提出一種新的檢測算法，將MCMC方法和基于統計學的離群點檢測算法進行相應的改進后結合起來檢測，具體如下：

(1) 使用恰當的MCMC方法對參數進行采樣，以解決由參數引起的錯誤問題。在使用MCMC方法時，選擇了隨機游走的M-H算法，并對其進行了相應的改進，使用格里汶科定理和Jeffreys先驗方法來克服求解分布函數和先驗分布函數的困難。

(2) 使用基于統計學的離群點檢測算法來解決檢測范圍的問題。在使用基于統計學的離群點檢測算法時，通過對控制區間進行相應的改進，以此克服區間過大等困難。

1 相關工作

1.1 偽裝缺失值

目前，隨著離群點檢測技術的廣泛應用，許多研究都是先對離群點進行分類后再進行檢測[11-13]，大大提高了檢測效率。Pearson[14]提出的一個新出現的數據質量問題——偽裝缺失值，它是一種特殊的缺失數據，指的是數據條目中不完全缺失但不能反映的值。文獻[14]對偽裝缺失值的分類具體如下：

(1) 超出范圍的數據值，例如在只接受負值的正值的屬性中隱藏缺失的值。

(2) 異常值，例如用非常大的值或非常小的值來偽裝缺失的值。

(3) 在使用的鍵盤上具有重復字符或彼此相鄰的字符，例如用5555555555代替一個電話號碼。

(4) 不協調數據類型的值，例如用數值偽裝缺失的字符串，反之亦然。

(5) 在數據范圍內隨機分布并在數據集中經常使用的有效值。

在上述每一種情況下，偽裝缺失數據都可以被視為outlier(案例(1)-案例(4))或inlier(案例(5))。本文主要講解上述偽裝缺失值的第五種情況的檢測方法。

1.2 MCMC方法

MCMC方法[15]主要包括Metropolis-Hastings算法(M-H算法)和Gibbs算法。其中M-H算法[16-19]是MCMC方法的核心，主要用于數據采樣。算法主要由以下三部分組成：

(1) 從建議分布生成建議(或候選)樣本。

(2) 基于建議分布和聯合密度，通過接受函數計算接受概率。

(3) 以概率接受建議(候選)樣本，或拒絕該樣本。

建議分布主要分為對稱分布和非對稱分布兩種，如果滿足式(1)，則建議分布為對稱分布，否則為非對稱分布。

q(xi|xi-1)=q(xi-1|xi)

(1)

對稱分布包括高斯分布、以鏈當前狀態為中心的均勻分布等；不對稱分布包括F分布等。

根據M-H算法的特征，給出了任一分布作為建議分布的似然函數(密度函數)、先驗分布和后驗分布。

根據建議分布，可以得出其先驗分布、似然函數分別為：

fp(xi)=prior(xi)

(2)

fl(xi)=likehood(xi,μ)

(3)

最后，根據先驗分布與似然函數的乘積確定后驗分布：

f(xi)=fp(xi)×fl(xi)=prior(xi)×likehood(xi,μ)

(4)

根據后驗分布函數，可以得到接受函數為：

α(xi|xi-1)=min{1,q(xi-1|xi)π(xi)/

q(xi|xi-1)π(xi-1)}

(5)

根據式(5)，決定接受還是拒絕該樣本。

1.3 基于統計學的離群點檢測算法

離群點檢測的統計學方法[20]的一般思想是：學習一個擬合給定數據集的生成模型，然后識別該模型低概率區域中的對象，把它們作為離群點。離群點檢測的統計學方法可以劃分成參數方法和非參數方法兩個主要類型，根據數據集以及實驗需求進行分析，最終選擇基于正態分布的一元離群點檢測方法。

該方法主要分為兩個步驟：

(1) 利用最大似然函數:

(6)

(7)

(8)

(2) 遍歷樣本集合，檢測樣本是否落在以下區間內:

(9)

該區間包含了大量的數據，所以如果樣本在區間內，則為正常點，否則為離群點。

2 基于MCMC方法的區間控制偽裝缺失值檢測算法

由于數據集有很多臟數據，導致數據集的參數會發生變化，如果直接利用參數對數據集進行分析，誤差就會很大。因此，本文將MCMC方法和基于統計學的離群點檢測算法結合，提出基于MCMC方法的區間控制偽裝缺失值檢測算法。本文的主要工作如下：首先采用M-H算法對參數進行采樣，然后根據采樣出來的參數通過基于正態分布的一元離群點檢測算法選取控制區間對數據樣本進行遍歷。算法的主要步驟如圖1所示。

圖1 本文方法的主要步驟

2.1 高頻率偽裝缺失值

為了使檢測效果得到較好的改善，對1.1節中的偽裝缺失值進行了進一步分類處理。以data.gov.uk數據集中Accident表中的部分數據為例來說明1.1節中偽裝缺失值的第五種類型，如表1所示。

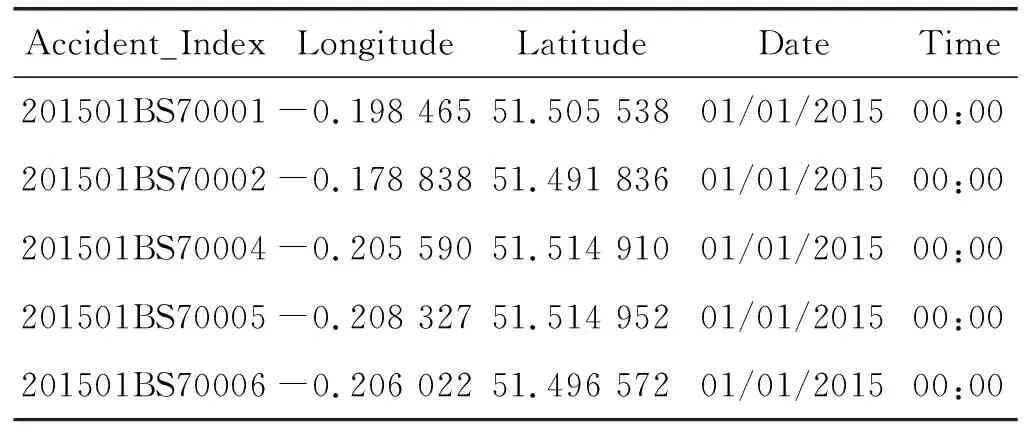
表1 data.gov.uk數據集中Accident表

可以看出，在Date列和Time列中，它們的值全部為01/01/2015和00:00，數據類型完全符合數據屬性，完全發現不了是錯誤值。但當與真實數據進行對比時，會發現數據值是錯誤的，這種就是在數據范圍內隨機分布并在數據集中經常使用的有效值(第五類)。此種偽裝缺失值給檢測工作帶來了巨大困難，它以一定的概率出現在正確值中，不容易被檢測到。因此本文主要對該種偽裝缺失值進行講解，并重新命名為高頻率偽裝缺失值。

2.2 參數采樣的方法(MCMC方法的改進)

當使用MCMC方法時，選擇的是M-H算法。M-H算法主要分為獨立抽樣的M-H算法、單變量的M-H算法和隨機游走的M-H算法，其中隨機游走的M-H算法[19]是MCMC方法中應用最廣泛的一種算法，通用性比較強，任何一種對稱分布都可以作為該算法的建議分布，由此產生的馬爾可夫鏈通常是遍歷的，所以本文選用的是隨機游走的M-H算法。

在使用隨機游走M-H算法時，最困難的問題是求數據集的概率密度函數和后驗分布函數。為了解決這兩個問題，本文的方法如下：

(1) 利用經驗分布函數和格里汶科定理確定分布函數，進而得到概率密度函數。

(2) 統一利用Jeffreys先驗確定方法確定先驗分布函數，得到后驗分布函數和接受函數。

接下來，以高斯分布為例來講述求解改進的M-H算法執行的主要過程，即參數采樣的主要過程。

Step1經驗分布函數。

定理1(格里汶科定理[21]) 設x1,x2,…,xn是取自樣本總體分布函數為F(x)的樣本，Fn(x)是其經驗分布函數，當時n→∞，有：

(10)

定理1表明，當n相當大時，經驗分布函數Fn(x)是總體分布函數F(x)的一個良好的近似。

在求概率密度函數時，首先求出了經驗分布函數，由于數據量比較大，根據格里汶科定理，由經驗分布函數近似得到了分布函數，進而通過分布函數得到了數據集的概率密度函數。

Step2建議分布。

在使用M-H算法時，首先需要確定建議分布類型，然后根據建議分布的不同類型，進行求解。

假設樣本服從高斯分布：

xi～N(μ,σ2)

(11)

進而可以得出其密度函數：

(12)

然后，根據密度函數可以得到似然函數：

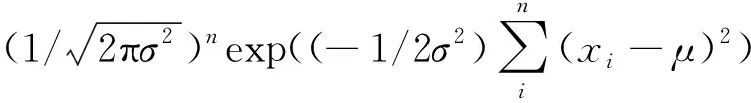
(13)

Step3先驗分布函數。

先驗分布函數的求解采用的是Jeffreys先驗確定方法[22]。首先，對樣本的似然函數取對數：

(14)

l(μ;σ2)=lnL(μ,σ2)=-n/2ln(2π)-

(15)

然后，求Fisher信息矩陣：

(16)

采用E(·)矩母函數方法[23]進行求解式(17)。

(17)

解得：

(18)

所以：

detI(μ;σ)=2n2σ-4

(19)

最后，根據先驗分布函數的求解公式：

π(θ)=[detI(θ)]1/2

(20)

解得樣本的先驗分布函數為：

(21)

Step4后驗分布函數。

根據似然函數和先驗分布函數的乘積，得出后驗分布函數：

(22)

Step5接受函數。

為了簡化計算，方便對接受函數進行化簡，在此考慮建議分布是否為對稱分布，主要采用偏度來進行判斷，具體如下。

偏度[23]是樣本數據分布偏斜方向和程度度量，是樣本數據分布非對稱程度的數字特征，計算公式為：

sk=E[(x-μ)3]/σ3

(23)

(1) 當sk=0，樣本數據為對稱分布。

(2) 當sk≠0，樣本數據為非對稱分布，如果sk>0,樣本數據為右偏，sk<0樣本數據為左偏。

如果建議分布是對稱分布，根據式(1)，可以將接受函數簡化為：

α(xi|xi-1)=min{1,π(xi)/π(xi-1)}

(24)

最后，根據接受函數，來決定接受還是拒絕樣本。

2.3 控制區間的確定方法(基于統計學的離群點檢測算法的改進)

本文主要檢測高頻率偽裝缺失值，因此本文根據M-H算法傳過來的參數，對基于統計學的離群點檢測算法進行反向應用，并對控制區間進行改進，將一個大區間分成幾個小區間的并集來控制數據遍歷，進而提高檢測效率。

具體方法如下：

Step6控制區間。

根據M-H算法所采樣到的參數，確定兩個區間：式(9)和式(25)。

(25)

第一個區間為根據基于統計學的離群點檢測算法確定的區間，第二個區間為置信區間[21]，置信度越大，置信區間越寬，通過調整置信度，控制區間，詳細說明如下：

當樣本x分布未知，但樣本數據較大時，根據中心極限定理，它可以近似為：

(26)

當σ2已知時，則μ的置信度為1-α的置信區間為：

(27)

當確定了兩個區間時，通過分析這兩個區間，發現區間如式(9)包含的數據樣本多于區間如式(28)的。

(28)

因此，將區間拆分成多個小區間并集，表示為：

(29)

確定小區間后，判定是否處于這些區間內：

(30)

如果一個數據樣本處于上述區間(式(30))中，則為高頻率偽裝缺失值，否則為正確值。

通過對各種分布的分析，對高斯分布的計算一目了然。這里以高斯分布為例進行說明。

當樣本分布為高斯分布時，區間式(9)將包含99.7%的正確數據，區間式(28)將包含95%的正確數據，因此區間式(9)比區間式(28)包含更多的數據。為了提高算法的精確度，根據數據樣本分布不同，通過設置不同的置信度來控制控制區間，其中不規格分布置信度設置為75%，規格分布置信度設置為85%(包括正態分布、卡方分布、t分布等)。

2.4 算法描述

首先通過改進的M-H算法對參數進行采樣；然后根據改進的M-H算法傳過來的參數，通過改進的基于統計學的離群點檢測方法確定控制區間式(31)。最后，在控制區間式(31)內，對數據對象進行遍歷。本文主要檢測高頻率偽裝缺失值，如果數據對象在控制區間內，則判定為高頻率偽裝缺失值；否則，判定為正常值。算法執行過程如算法1所示。

算法1本文算法

輸入：數據集X中的數據對象x。

輸出：數據集X中偽裝缺失值集合G。

1.forxinXdo

2.根據Jeffreys先驗確定方法計算數據對象x的先驗分布函數；

3.根據式(22)計算數據對象x的后驗分布函數；

4.根據式(5)計算數據對象x的接受函數；

5.根據式(31)計算數據對象x的控制區間；

6.ifx∈區間式(31)

7.將數據對象x添加到偽裝缺失值集合G中；

8.end if

9.end for

10.輸出高頻率偽裝缺失值集合G

3 實驗驗證

3.1 相關定義

為了能夠明顯地看出實驗效果，定義了三個評價指標，即查準率(precision)、查全率(recall)和F1-Measure。設輸入的樣本總數量為m，輸出的高頻率偽裝缺失值的數量為n，檢測到的高頻率偽裝缺失值的數量為o。具體計算公式如下：

(1) 查準率(precision)，記為P：

P=o/n

(31)

(2) 查全率(recall)，記為R：

R=o/m

(32)

(3) F1-Measure，記為F1：

F1=(2PR)/(P+R)

(33)

相對而言，如果算法的查準率、查全率和F1-Measure都比較高，則證明該算法優于其他算法，具有良好的可用性。

3.2 數據集選擇

為了驗證算法的檢測效果，并考慮到數據分析在各個領域的責任的重要性，本文選擇Mass.gov數據存儲庫中3張表、UCI-ML數據存儲庫中4張表和Data.gov.uk數據存儲庫中6張表，共13個數據集進行比較實驗，主要涉及醫療、交通和教育等領域。在進行實驗前手工注釋了每個數據集中的高頻率偽裝缺失值。

3.3 實驗對比

實驗從四個方面測試了本文算法：Ex-1：算法的效率(查準率、查全率和F1-Measure)；Ex-2：與dBoost算法的比較；Ex-3：與DiMaC算法的比較；Ex-4：與FAHES算法的比較(Random DMVs)；Ex-5：與k均值聚類算法的比較(KMOR算法)。

(1) Ex-1：算法的效率(查準率、查全率和F1-Measure)。為了驗證本文算法的效率，在Mass.gov、UCI-ML和Data.gov.uk三個數據存儲庫中所選擇的數據集上進行了相應的實驗。為了方便進行實驗，首先通過數據樣本映射的方式對數據集進行分析，通過分析得到data.gov.uk數據存儲庫上所選擇的數據集呈正態分布，Mass.gov和UCL-ML數據存儲庫上所選擇的數據呈不規則的分布。通過對數據集的分析，可以知道在data.gov.uk數據存儲庫上所選擇的數據集進行實驗會比較容易些，可以直接得到數據樣本的概率密度函數，根據概率密度函數求出似然函數，再根據似然函數求出先驗分布函數，在進行求解先驗分布函數時，由于數據樣本所屬分布不同，求解先驗分布函數不夠準確，導致實驗效果不好，而本文所采用Jeffreys先驗確定方法，它在不同分布中無信息即可確定先驗分布函數，提高了檢測效率和算法執行所用的時間。根據似然函數和先驗分布函數計算出后驗分布函數和接受函數，并通過接受函數得到所需要的樣本均值和樣本方差，并將置信度設置為85%，最后通過區間式(9)和區間式(28)確定區間并在區間內對數據樣本進行遍歷。而Mass.gov和UCL-ML數據存儲庫上所選擇的數據集呈不規則分布，無法直接計算出概率密度函數，導致無法進行實驗，而經驗分布函數和定理確定其分布函數，進而可以得到概率密度函數，然后一步步求出似然函數、先驗分布函數、后驗分布函數、接受函數，并通過接受函數得到所需要的樣本均值和樣本方差，由于是不規則分布，因此將置信度設置為75%，最后結合區間式(9)和區間式(28)所確定遍歷區間對數據樣本進行遍歷。

因為本文算法所檢測的目標是高頻率偽裝缺失值，它通常偽裝成正確的值并以較高的頻率(出現頻率低于正常值的概率)出現在數據集中，用以往的離群點檢測算法或偽裝缺失值檢測算法進行檢測結果不盡人意，因為它們所能檢測到的僅僅是離群點或低頻率偽裝缺失值，而高頻率偽裝缺失值常常被誤認為正常值檢測不到。而本文算法通過區間式(9)和區間式(28)確定了區間式(31)，即控制區間，縮小了檢測范圍。讓數據樣本在控制區間內進行遍歷，如果數據樣本在控制區間內，則可以找出高頻率偽裝缺失值。

遍歷數據樣本結束后，根據式(27)和式(28)，求出本文算法在Mass.gov、Data.gov.uk和UCI-ML三個數據存儲庫中13個數據集的平均查全率和平均查準率，如表2所示。

表2 三個數據存儲庫上的查準率、查全率和F1-Measure

(2) Ex-2：與dBoost算法的比較。dBoost算法并非為離群點檢測而設計，進行檢測時檢測到非偽裝缺失值，導致檢測效果較差，而本文算法通過對控制區間的改進，縮小了檢測范圍，為檢測偽裝缺失值所設計，通過表3中的對比可以看出，本文算法的查全率提高了很多。

表3 與dBoost算法的對比

(3) Ex-3：與DiMaC算法的比較。DiMaC算法主要檢測偽裝缺失值，但是它沒有對偽裝缺失值進行分類，導致其檢測范圍太大，檢測效率差，而本文算法對偽裝缺失值進行了分類并且取得較好的檢測效果。檢測效果對比如表4所示。

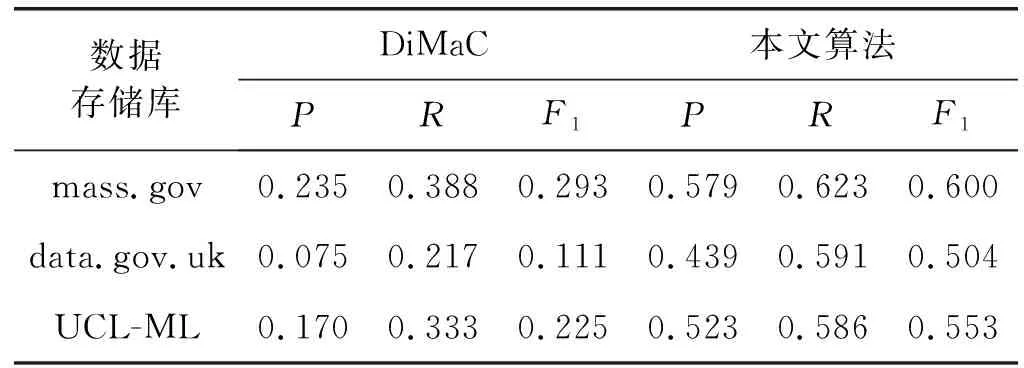
表4 與DiMaC算法的對比

(4) Ex-4：與FAHES算法的比較(Random DMVs)。因為FAHES算法是對偽裝缺失值分類后進行檢測，所以它要優于前兩種算法，但是由于分類不夠細致，仍然會有很多的錯誤值出現在分類之外，導致檢測效果略差，而本文算法的檢測目標明確，主要檢測高頻率偽裝缺失值，檢測效果有很大的改善，如表5所示。

表5 與FAHES算法的對比

(5) Ex-5：與k均值聚類算法的比較(KMOR算法)。為了驗證本文算法的權威性，選擇了Gan等[26]優化的KMOR算法。由于本文主要檢測高頻率偽裝缺失值，KMOR算法可能將所有偽裝缺失值視為一個較大的簇，并將它們視為正常值，導致檢測效果差。比較結果如表6所示，通過對查準率、查全率和F1-Measure的比較，本文算法的檢測效果明顯優于KMOR算法。

表6 與KMOR算法的對比

根據表3-表6中在Mass.gov、Data.gov.uk和UCI-ML三個數據存儲庫中查全率、查準率和F1-Measure的對比，繪制了對比圖，如圖2-圖4所示。可以看出，本文算法優于其他四種算法。

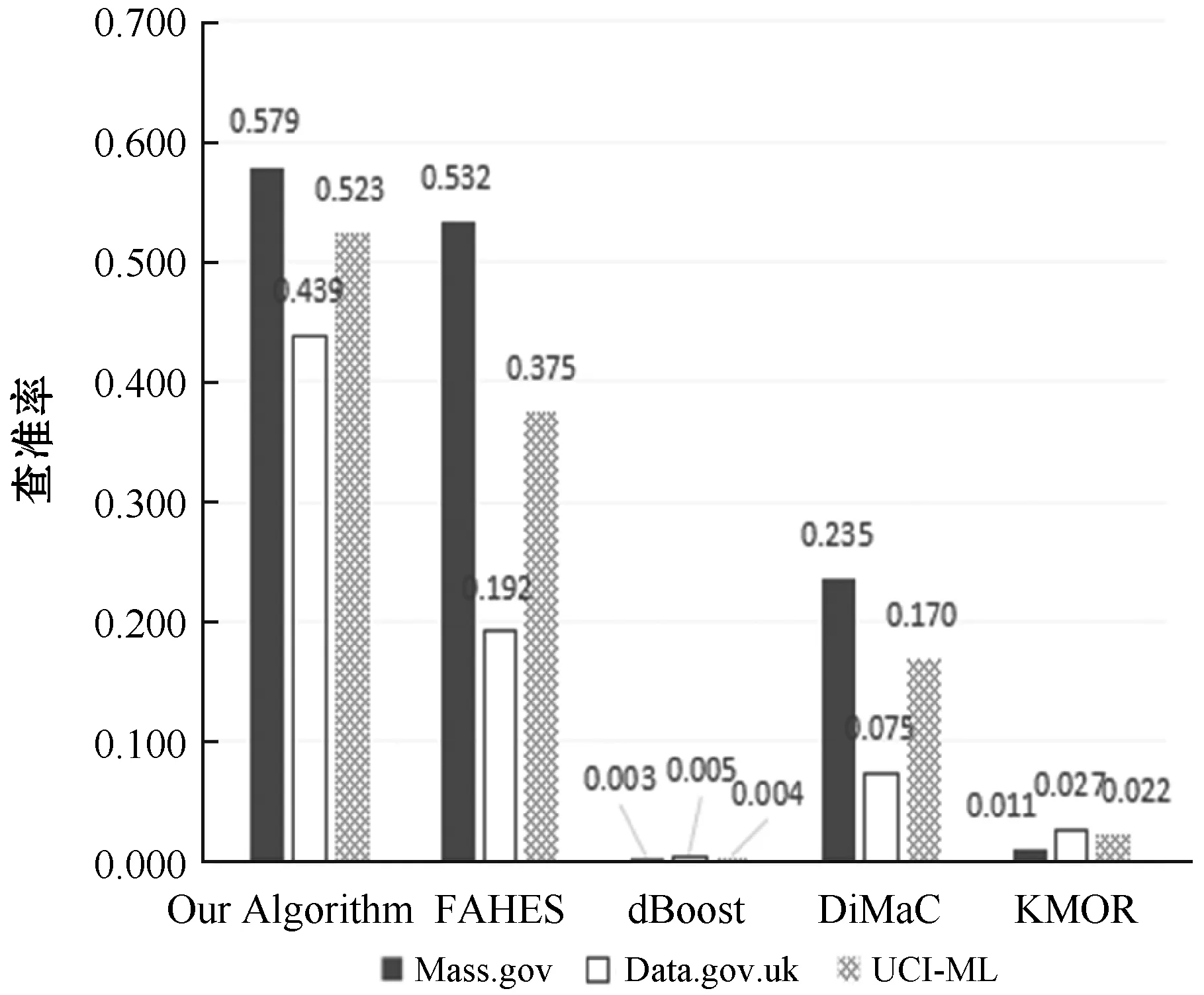
圖2 五種算法的查準率對比

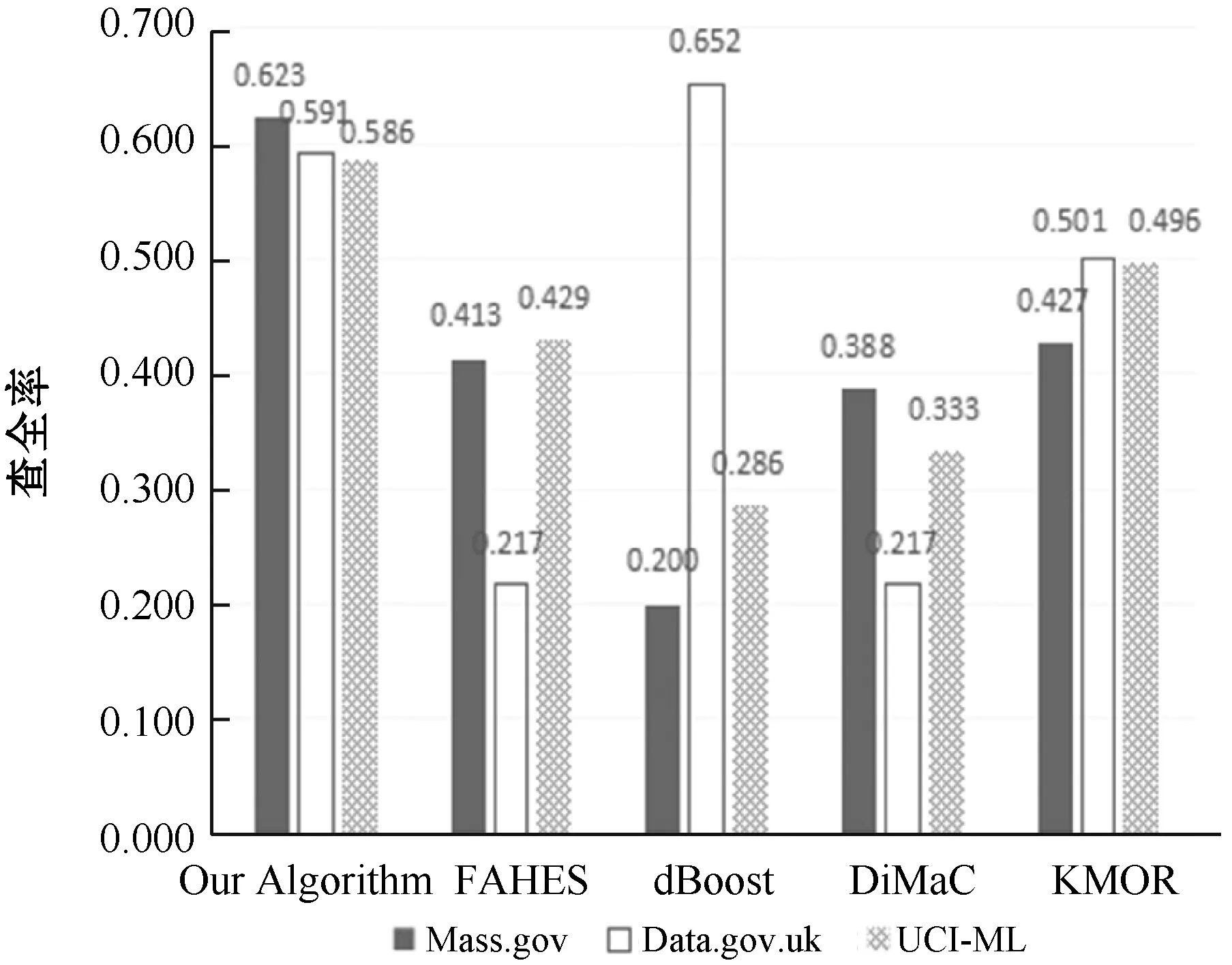
圖3 五種算法的查全率對比

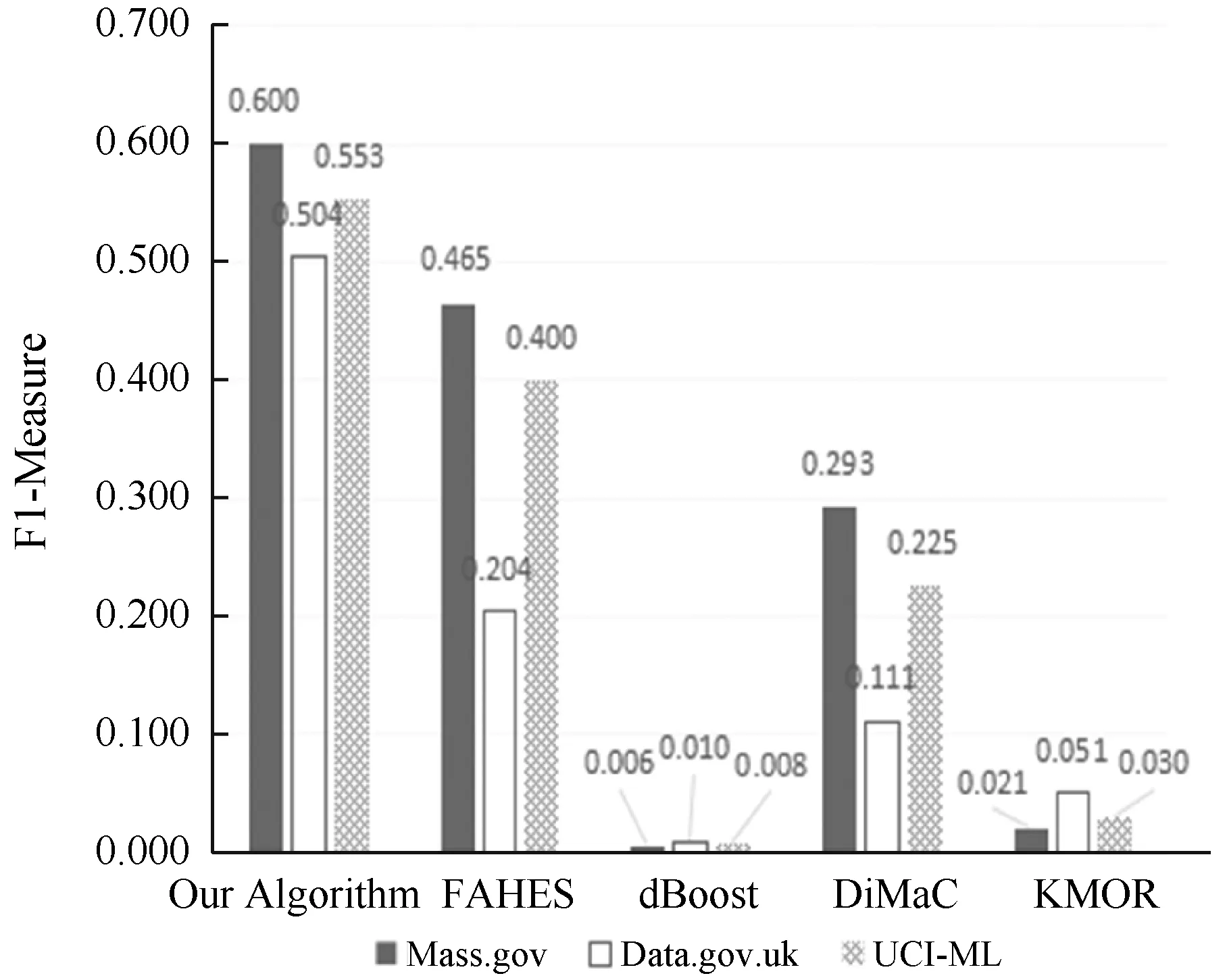
圖4 五種算法的F1-Measure對比

4 結 語

本文主要是解決檢測高頻率偽裝缺失值的問題，為此本文提出基于MCMC方法的區間控制偽裝缺失值檢測算法，將改進的MCMC方法和改進的基于統計學的離群點檢測算法結合在一起進行檢測。首先采用改進的MCMC方法對樣本進行參數采樣，然后根據采樣所得的參數采用改進的基于統計學的離群點檢測算法確定控制區間，最后在確定的控制區間里對數據樣本進行遍歷。此外，利用Mass.gov、UCL-ML和Data.gov.uk三個數據存儲庫中的數據集進行對比實驗，驗證算法的權威性，通過實驗結果可以看出，本文算法的查準率、查全率和F1-Measure有了明顯改善。下一步，本文的工作將主要側重于解決如何檢測低概率的有效值類偽裝缺失值，進一步提高算法的檢測效果。