基于DTW-KNN的機械通氣無效吸氣努力檢測

潘 清 龔 強 陸 飛 方路平 葛慧青

1(浙江工業大學信息工程學院 浙江 杭州 310023)2(浙江大學醫學院附屬邵逸夫醫院呼吸治療科 浙江 杭州 310016)

0 引 言

重癥監護室(Intensive Care Unit, ICU)是保障重癥病人生命活動的最后一道防線。呼吸機是ICU里最重要的生命支持設備[1]。為最大程度保證病人生命安全，正確使用呼吸機，確保高質量的人機交互至關重要[2]。但是，使用呼吸機進行輔助通氣的重癥病人的生理呼吸周期與呼吸機的送氣周期可能不一致，會產生人機不同步現象[3]。人機不同步在呼吸機使用過程中出現頻率較高[4-8]。文獻[5]研究結果顯示，異步指數(不同步事件除以總呼吸率)大于等于10%的患者約占呼吸機治療人數的24%。人機不同步可能會導致患者與呼吸功能高度相關的肌肉組織損傷，進而導致吸氣相關的肌肉無法提供正常吸氣時所需的力量，造成患者無法脫離呼吸機獨立呼吸等諸多病人無法接受的后果[9-10]。研究自動檢測機械通氣人機不同步能夠及時提示醫護人員調整呼吸機的各項參數設置，減少人機不同步的發生，改善病人預后，對ICU臨床工作具有重要的意義。IEE是最常見的人機不同步類型之一，其在呼吸機波形上的表現為氣道壓力波形呼氣相凹陷的同時伴隨流速波形在呼氣相突起。由于病人的病情及每一次呼吸的狀態均存在不確定性，造成IEE事件的發生程度以及在呼氣相的發生時間有所差異，導致IEE特征的幅值、特征在呼氣相的位置有所變動，使得IEE事件的氣道壓力以及流速波形具有非平穩特征。而且，病人呼吸周期存在變異性，將導致呼吸序列不等長。常用的IEE檢測方式是依靠專業人員在床邊觀察和評估呼吸機波形[11-12]。早期IEE的自動檢測方法主要是基于規則的[5，13]。Thille等[5]將IEE定義為氣道壓突然下降(≥0.5 cmH2O)的同時流速也隨之降低，并且呼氣期間產生的吸氣努力強度不足以觸發呼吸機為患者送氣，無法開啟新的呼吸周期。Chen等[13]認為，在呼氣期間，當最大流速偏差或者最大氣道壓偏差超過預設閾值時，即發生IEE事件。近年來，隨機森林(Random Forest,RF)及自適應增強(Adaptive Boosting,AdaBoost)算法也被一些學者應用于IEE的自動檢測，取得了較好的效果[14]。但上述方法在IEE檢測上均存在一定局限性：在床邊觀察和評估呼吸機波形的方法需要花費大量的醫護人員資源；基于規則的檢測方法對噪聲比較敏感，且其性能受閾值選擇影響較大；基于RF和AdaBoost的檢測方法需要提取特征，而所提特征可能存在信息泄露的問題。為解決上述方法在IEE檢測上的不足，本文提出一種基于DTW-KNN的IEE檢測方法，該方法通過計算樣本間的相似性對呼吸波形進行分類。

DTW算法基于動態規劃的思想，解決了不等長序列的模板匹配問題[15]，適用于不等長序列的相似性測量。各種基于DTW方法已成功用于心電信號、腦電信號等生物信號時間序列及非生物信號的分類與識別中[16-19]。文獻[16]使用DTW對ECG幀進行模板匹配，實現ECG信號的幀分類，實驗達到了1.33%的分類殘差的良好分類結果。文獻[17]中，DTW更是成功地區分了各種心律不齊的心電信號。以上研究結果證明DTW在具有非平穩特征的生物信號分類中具有良好的性能。

因此，針對呼吸序列的不等長及非平穩特征的問題，本文引入DTW算法計算呼吸序列之間的相似性距離，以此來度量兩條序列的相似性。在同一實驗數據下，基于規則的方法和AdaBoost方法檢測IEE事件的準確率均不足90%。RF的IEE檢測準確率為92.5%。而本文提出的DTW-KNN算法對IEE的檢測準確率達到96.9%。

1 基于KNN和DTW的IEE檢測算法

1.1 IEE波形特征

IEE是最常見的人機不同步類型之一，其氣道壓力波形與流速波形均存在相應特征：氣道壓力波形呼氣相凹陷，與此同時流速波形在呼氣相突起。由于患者的病情和呼吸狀態存在不確定性，造成IEE事件的發生程度以及在呼氣相的發生時間有所差異，導致IEE特征的幅值、特征在呼氣相的位置有所變動，使得IEE事件的氣道壓力及流速波形具有非平穩特征。而且，病人呼吸周期存在變異性，將導致呼吸序列不等長。

連續五次呼吸的氣道壓力波形、流速波形及波形特征如圖1所示，其中IEE波形特征由黑色圓圈標出。可以看出，IEE事件的呼氣相波形與非IEE呼吸相波形相比，兩者之間的形狀差異較大，并且兩個IEE事件之間的特征表現也有所不同，即氣道壓力以及流速波形具有非平穩特征。

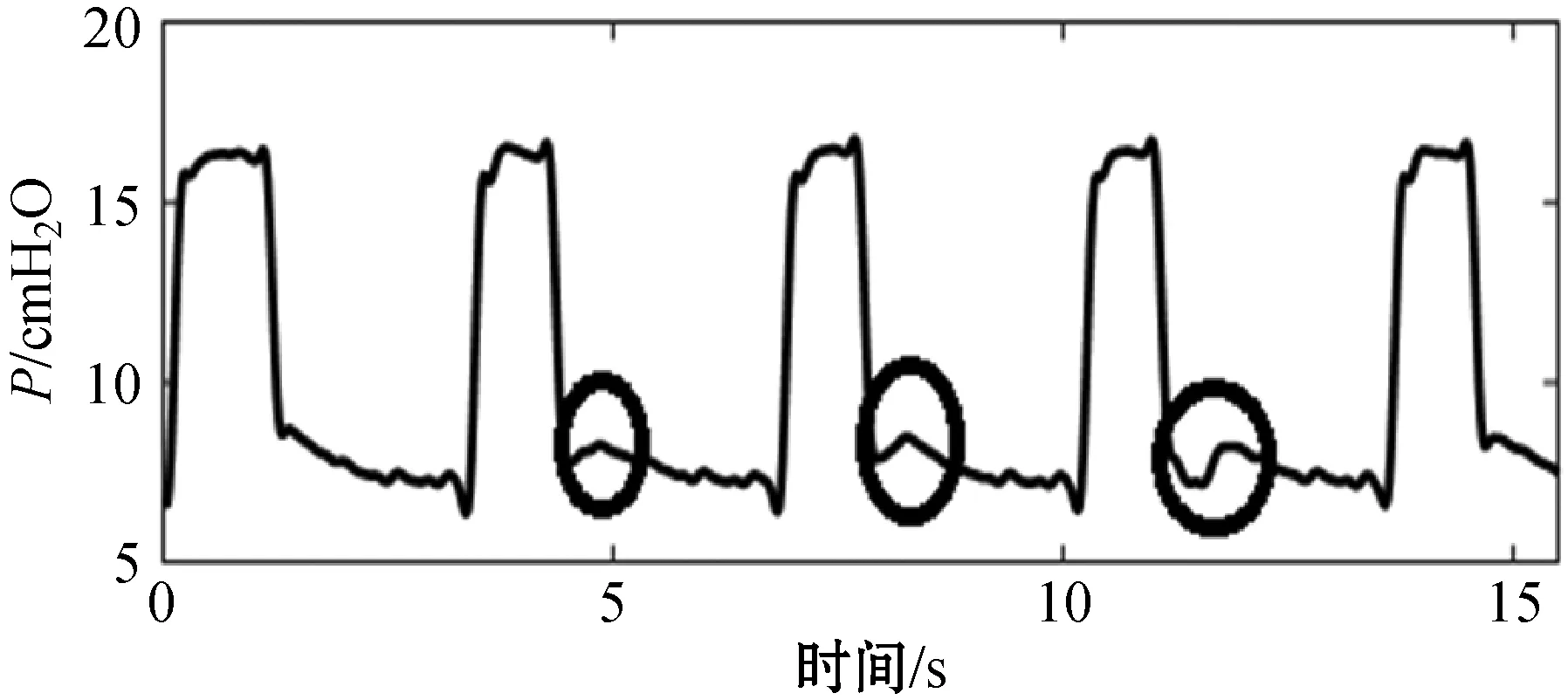
(a) 氣道壓波形

(b) 流速波形圖1 連續五次呼吸波形

1.2 數據預處理

在臨床上，針對病人不同的病情，需要給予不同強度的機械通氣支持，即不同病人的氣道壓力和流速水平均不相同，這將導致后續使用DTW計算兩條呼吸序列的相似性距離產生較大偏差。圖2展示了呼吸序列經過預處理與未經過預處理的兩條IEE序列及IEE序列、非IEE序列之間的DTW距離，其中：圖2(a)、(b)分別給出了未經預處理的兩條IEE序列以及IEE序列、非IEE序列之間的DTW距離；圖2(c)、(d)分別給出了經過預處理的兩條IEE序列以及IEE序列、非IEE序列之間的DTW距離。可以看出，未經過預處理的兩條IEE序列的DTW距離為441.94，大于IEE序列與非IEE序列之間的DTW距離411.59；而經過預處理之后的兩條IEE序列的DTW距離為10.92，小于IEE序列與非IEE序列之間的DTW距離18.51。由上述結果可知，對呼吸序列進行預處理之后在進行相似性距離計算時，得到的結果更能反映真實的波形相似情況。

(a) DTW距離:441.94 (b) DTW距離:411.59

(c) DTW距離:10.92 (d) DTW距離:18.51圖2 預處理前后兩條同類別序列以及不同類別序列之間的DTW距離對比

因此，在進行數據分析之前需先對波形進行歸一化，消除由于波形幅度不同而造成的差異。本文根據式(1)對呼吸序列S(s1,s2,…,sn)采用Z-score方法進行數據標準化，避免因氣道壓力、流速水平不同引發的問題。

(1)

1.3 K-最鄰近算法(KNN)

KNN算法[20]思想簡單明了，分類準確率較高，錯誤概率的上限是貝葉斯錯誤概率的兩倍，被認為是向量控件模型下最好的分類器，在醫學以及圖像識別與分類等領域都展現其良好的分類效果[21-22]。其基本思想是：計算待分類樣本與各個訓練樣本之間的相似性，找出訓練樣本中與待分類樣本最相似的K個樣本，最后根據得到的K個樣本的類別確定待分類樣本的歸屬。其算法描述為：首先，計算測試序列樣本與各個訓練數據樣本之間的相似性距離，并按照從小到大的順序對所有相似性距離進行排序；然后，選取前K個最小距離所對應的測試序列樣本，確定所選取的前K個最小距離所對應的測試序列樣本所在類別的出現頻次；最后，將出現頻率最高的類別作為測試出序列樣本的預測分類。圖3為KNN在本研究中分類示意圖，其中：矩形和三角形分別代表不同類型的呼吸波形數據，圓形為待分類呼吸波形。

圖3 KNN算法示意圖

待分類樣本與2個三角形樣本和1個矩形樣本最相似，根據KNN算法，待分類樣本被分為三角形樣本。同時，對于不同的K值，KNN算法的分類結果是不一樣的。

1.4 動態時間規整(DTW)

在KNN算法中需要計算樣本之間的相似性。歐氏距離是最常用的樣本相似性度量方法。等長時間序列Q(q1,q2,…,qn)和C(c1,c2,…,cn)的歐氏距離ED(Q,C)計算公式如下：

(2)

應用式(2)要求進行對比的兩樣本之間具有相同的序列長度。但是，由于病人呼吸周期存在變異性，導致采集的呼吸序列長短不一，因而無法使用歐氏距離來度量序列的相似性。通過插值和重采樣的方法盡管能夠使兩段序列具有相同的長度，但插值和重采樣方法僅僅使不等長序列變成等長序列而已，并未考慮到兩條序列采樣點之間的距離的相對大小關系，從而導致了序列各個采樣點之間的無規則偏移，進而造成兩條序列相似部分采樣點之間無法較好地對齊，使得原本相似的兩條序列之間的相似性距離偏大。DTW算法基于動態規劃的思想，解決了不等長序列的模板匹配問題，適用于不等長序列的相似性測量。各種基于DTW方法已成功用于心電信號、腦電信號等生物信號的分類與識別中。文獻[16]使用DTW對ECG幀進行模板匹配，實現ECG信號的幀分類，實驗達到了1.33%的分類殘差的良好分類結果。在文獻[17]中，DTW更是成功地區分了各種心律不齊的心電信號。以上研究結果證明DTW在具有非平穩特征的生物信號分類中具有良好的性能。因此，對于同樣具有非平穩特征的呼吸信號，本文以DTW距離來度量不等長呼吸序列之間的相似性。對于兩條不等長時間序列Q(q1,q2,…,qn)和C(c1,c2,…,cm)，DTW通過動態規劃能夠找到Q和C之間的最佳規整路徑，再通過式(3)得到最小累加距離D(i,j)。

(3)

式中：d(qi,cj)=(qi-cj)2。最終，可由式(4)計算兩序列的DTW距離DTW(Q,C)。

(4)

對于兩條序列Q(q1,q2,…,qn)和C(c1,c2,…,cm)，兩者經過動態規劃算法得到的最佳規整路徑WP={WP1,WP2,…,WPk},max(m,n)≤k≤m+n-1，必須嚴格服從以下約束：

(1) 邊界條件。所選的路徑必須從WP1=(1,1)出發，在WPk=(n,m)結束。

(2) 連續性。如果路徑當前點為(x1,y1)，那么對于路徑的下一個點(x,y)需要滿足(x-x1)≤1且(y-y1)≤1。

(3) 單調性：如果路徑當前點為(x1,y1)，那么對于路徑的下一個點(x,y)需要滿足(x-x1)≥0和(y-y1)≥0。

圖4為兩條不等長呼吸序列及兩者的最佳規整路徑。其中：圖4(a)、(b)為標準化的呼吸流速序列，圖4(c)為最佳規整路徑。可以看出，動態規劃對時間上的壓縮和延伸是不敏感的。因此，采用了動態規劃思想的DTW能很好地度量兩條不等長序列的相似性。

圖4 不等長呼吸序列的最佳規整路徑示意圖

圖5為Z-score標準化之后兩條呼吸流速序列、經過重采樣對齊、插值法對齊以及DTW對齊前后的對比圖。可以看出，當采用重采樣以及插值法實現兩條不等長呼吸流速序列的對齊時，如圖5(b)、(c)所示，這兩種方法并沒有把波形的相似部分較好的對齊，盡管兩條序列的長度變得一樣，但是波形的對齊效果比圖5(a)中直接標準化之后的波形對齊效果還更差。而兩條不等長序列經過DTW之后，相比于重采樣和插值法的對齊效果，兩條原本相似的不等長的呼吸流速序列的對齊效果提升較大，其對齊效果如圖5(d)所示。

(a) 兩條原始呼吸流速 (b) 經過重采樣方法對齊的呼吸流速

(c) 經過插值法對齊的呼吸流速 (d) 經過DTW對齊的呼吸流速圖5 呼吸流速對齊方法對比圖

因此，經過DTW對齊之后，能夠很好地度量兩條序列的相似性距離，從而可以用于KNN算法中的相似度度量。

1.5 實驗材料

在重癥監護室中采集了17名使用Puritan Bennett 840呼吸機進行機械通氣的重癥患者的氣道流速波形數據。其中成年男性11名，成年女性6名，患者平均年齡為64.5歲。研究得到浙江大學醫學院附屬邵逸夫醫院倫理委員會審查通過(No.20190916-16)。表1展示了所選病人的相關信息。

表1 選取病人信息表

對上述篩選的數據進行標注，先由5名資歷較低的醫生進行第一輪的預標注，后由2名資歷較高醫生對第一輪的標注結果進行審核，以確保標注結果的準確性。最后形成IEE數據集和非IEE數據集兩個數據集，IEE數據集中包含1 032次呼吸流速波形數據，非IEE數據集中包含1 031次呼吸流速波形數據。

1.6 評價方法

本文以十折交叉驗證評價算法的性能。將標注后的數據隨機分為10份，選取其中1份作為測試序列樣本，其余9份作為訓練序列樣本；然后依次對每一份測試序列樣本與訓練序列樣本分別做Z-score標準化后，再通過DTW計算兩者的相似性距離，選取前K個最小距離的訓練序列樣本；最后將其中出現次數最多的類別標簽作為測試序列樣本的類別標簽。圖6為本研究方法流程。

圖6 研究方法流程

本實驗采用準確率、靈敏度、特異性以及F1得分來衡量算法性能。各指標計算方式如下：

(5)

(6)

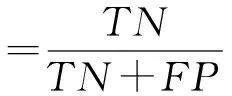
(7)

(8)

式中：TP表示真陽性數量；TN表示真陰性數量；FP表示假陽性數量；FN表示假陰性數量。

1.7 算法對比

為了驗證所提出的算法的優越性，本文將其與傳統的基于規則的算法及基于RF和AdaBoost的算法進行對比。

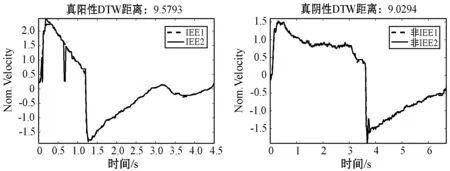
Chen等于2008年提出一種基于規則的IEE檢測方法，其基本思想是：通過計算呼吸流速呼氣相的極大值與其之后的最小值的差值和設定閾值的大小關系來檢測該次呼吸是否發生IEE事件。該算法描述為：首先檢測呼吸流速序列的呼氣開始點，獲取流速呼氣相序列H(h1,h2,…,hk)，并計算H的所有極大值Hm及極大值索引m,1

Sottile等[14]利用RF算法和AdaBoost算法實現了IEE的自動檢測。本文重現了其算法并應用于本文數據集上進行性能對比。首先，提取IEE檢測所需的特征，包括呼吸周期、吸氣末氣道壓、吸氣末流速、吸氣末潮氣量等時間、氣道壓、流速及潮氣量四大類特征參數(具體參數見文獻[14]的附錄補充材料)。隨后構建RF和AdaBoost預測模型，通過網格搜索方法進行模型參數調優。最后基于所構建的模型對測試樣本進行類別判定。RF基本思想是：從訓練集中隨機有放回地抽取與訓練集數目相等的樣本以及隨機選取特征集里面的少量IEE特征來對決策樹進行訓練，反復執行，產生多棵決策樹；將未參加決策樹訓練的訓練集樣本作為測試樣本，再基于少數服從多數原則，對所有決策樹的輸出結果進行投票以得到測試樣本的預測分類結果。AdaBoost基本思想是：根據訓練集中每個樣本的分類是否正確以及最后一次整體分類的準確性來更改數據分布并確定每個樣本的權重。權重已修改的新數據集將發送到下一個弱分類器進行訓練，最后算法將組裝這些不同的弱分類器以形成更強的分類器作為最終決策分類器。

2 實驗結果與分析

為驗證本文提出方法的性能，將本文方法與Chen等[13]提出的基于規則的方法及Sottile等[14]提出的基于RF和AdaBoost的方法進行比較。

本文算法中，K取1～15(步長為2)，不同K值結果在表2中展示。在各種K取值情況下，準確率有所差異，隨著K值的增大，準確率逐漸下降，但均在95%以上。K=15時準確率最低，為95.3%；K=1時準確率最高，為96.9%。這表明，IEE樣本類內差異范圍較大，而與非IEE樣本的類間差異范圍不大，K取較大值時容易出現部分IEE波形與較多的非IEE樣本更相似而錯分的情況。

表2 基于DTW-KNN方法在不同K值下對IEE的檢測性能

最優DTW-KNN方法與其他方法比較的結果如表3所示。基于規則的方法和AdaBoost方法檢測IEE事件的準確率均不足90%。RF的IEE檢測準確率為92.5%。本文提出的DTW-KNN算法對IEE的檢測準確率達到96.9%，優于其他方法。

表3 實驗對比結果

本研究也嘗試對檢測結果里面的誤分樣本進行分析。圖7為使用DTW-KNN算法對不同呼吸流速序列測試樣本進行檢測的分類結果示意圖。圖中的訓練數據樣本均為測試樣本與訓練集所有樣本的最小DTW距離樣本。圖7(a)、(b)分別為IEE事件的正確檢測與非IEE事件的正確檢測示意圖，圖7(c)、(d)分別為IEE事件與非IEE事件的錯誤檢測示意圖。可以看出，經過DTW對齊之后的兩個不同類別的序列樣本只是在IEE事件呼氣相流速波形特征表現處有微小的差異，在波形其他地方基本沒有差別。這表明，IEE事件各個亞類樣本之間的差異比較明顯，而IEE事件各個亞類與非IEE事件樣本之間的差異較小。當某個IEE事件亞類中只包含單條呼吸序列樣本的時候，將會導致該IEE事件亞類的單條序列樣本與非IEE事件的樣本的相似性距離達到最小，造成DTW-KNN算法發生呼吸序列樣本的錯誤檢測。

(a) (b)

(c) (d)圖7 樣本分類結果圖

3 結 語

本文提出的基于DTW-KNN的IEE檢測方法相比于文獻報道的其他方法更加簡單，無須設置各類參數或提取復雜的特征，且準確率更高。基于規則的機械通氣IEE檢測方法需要選擇合適的閾值方能達到最佳效果。RF、AdaBoost等方法需要人工提取波形特征，特征是否具有代表性及特征計算的準確性均可能影響算法性能。而基于DTW-KNN可以直接依賴于呼吸波形的原始數據，無須提取特征或設置復雜的閾值。研究結果表明，較基于規則的方法及RF和AdaBoost方法相比，基于DTW-KNN的IEE檢測方法在準確率上有一定優勢。

DTW-KNN方法也存在以下不足：首先，KNN方法對K值比較敏感，使用KNN方法時也需要對K值進行小范圍閾值的掃描，消耗一定時間；其次，呼吸氣道壓波形數據也包含一定的IEE特征。但是本實驗只使用了IEE特征表現更明顯的流速波形數據，未使用氣道壓特征。在后續研究中，可針對上述不足之處進行優化，以進一步提升本研究提出的IEE檢測算法的性能。