基于梯度博弈的網絡化軟件優化機制
舒 暢 李青山 王 璐 王子奇 計亞江
(西安電子科技大學計算機科學與技術學院 西安 710071)
(shuchang@stu.xidian.edu.cn)
隨著互聯網的普及和移動技術的發展,當前軟件技術的發展呈現出了明顯的網絡化趨勢,越來越多的軟件應用選擇將業務或服務拆分后布置在不同的硬件設施上,通過互聯網通信協同完成工作,以實現更多樣化的功能.這類以網絡為媒介,以信息或服務資源為元素,以元素間的協同與互操作為構造手段,所建立的軟件密集型混合系統被稱為網絡化軟件[1].《中國互聯網發展報告(2021)》顯示,2020年我國工業互聯網市場規模已超9 000億元,物聯網市場規模達1.7萬億元,網絡化軟件的研究和發展有著廣闊的前景.
近年來,互聯網應用規模擴展迅速,網絡化軟件在互聯網中的部署越來越復雜,節點故障、通信擁塞、激增的用戶請求等突發因素為軟件的平穩運行帶來了巨大挑戰,導致軟件性能和服務質量的下降,造成重大的損失.例如,2019年6月,谷歌的云服務器出現約4 h的宕機故障,大量基于該服務的網站或應用服務加載緩慢、無法登錄,其中,大型視頻網站YouTube的全球觀看人數減少了10%;2021年3月,蘋果App Store,iCloud等服務出現大規模故障,大量用戶訪問相關服務緩慢或失敗.因此,網絡化軟件需要實現優化調整功能,主動調節各類參數,以保障軟件的正常運行,防止性能下降,提高系統的穩定性.
網絡化軟件部署在異構的聯網設備上,根據功能或服務范圍由數量不等的計算設備組成軟件節點,完成發送、匯集與處理數據的任務.軟件節點的大量部署使網絡化軟件產生了高度分布的特征.在此背景下,網絡化軟件的發展呈現出去中心化的趨勢,系統架構越發開放和平等,系統中每個節點高度自治,不具備強制性的中心控制[2].然而,由于網絡化軟件高度分布的特點,軟件節點之間存在的通信延遲阻礙了節點間的信息共享,導致各個節點在進行自主優化調整時出現個體與集體信念的不一致,為網絡化軟件系統的優化調整帶來了困難.
針對網絡化軟件性能優化中存在的節點間信息交流問題,本文研究了一種基于多智能體博弈的分布式優化框架,將智能體設置在不同的軟件節點上,各個智能體使用有限的信息估計系統狀態并做出決策對軟件的參數進行管理,實現軟件性能的優化.此外,本文針對現有方法易發散、參數選取困難的問題提出了自適應步長機制和強制協調機制,根據各個智能體的估計誤差調整當前決策尋優步長,防止由于智能體之間估計偏差過大帶來的發散問題,同時保證了方法的收斂速度.
1 相關工作
目前軟件在線優化的研究主要集中于如何通過合理的資源分配和任務調度提高軟件的服務質量或降低資源消耗和運營成本.阿里巴巴的云服務器集群采用了集中式任務管理機制,在阿里巴巴的混部集群中,由Sigma和Fuxi兩種管理中心匯總各個服務器的運行信息并對進程合理調度以提升資源的利用率[3];Sahni等人[4]提出了一種啟發式的云計算資源彈性伸縮方法,該方法通過資源提供歷史和在線的工作負載分析估計后續任務的資源需求,之后使用貪心算法給出一組最優的資源配置,以更低的資源消耗和更高的資源利用率滿足軟件的服務質量需求;Chen等人[5]基于反饋控制實現了一種組合服務的自優化機制,設置函數數值化計算當前的服務質量,根據計算結果使用比例積分微分控制器對影響服務質量的因素進行重要性排序,產生優化調整的策略;Das等人[6]針對流處理系統的容錯和效率問題,提出了一種基于不動點迭代的控制算法,自適應地調整批處理作業的大小,使工作負載能夠適應系統當前的情況.現有研究以軟件控制的自動化和智能化為目的,但大多著眼于使用集中控制方法對軟件系統進行調控,然而,這種方法無法完全適用于愈發龐大、愈發復雜的網絡化軟件系統.首先,在集中控制的情況下,中心控制節點的故障將會導致調控機制停擺,缺乏可靠性;其次,集中為所有軟件節點提供控制策略需要收集大量的節點信息并產生巨大的計算開銷,效率低下;最后,在部署或移除軟件節點時,需要為中心節點更新控制邏輯,難以應用于動態變化的大型系統.
本文采用多智能體博弈的方法對網絡化軟件進行優化,將智能體設置在不同的軟件節點上,實現分布式的優化決策與控制,相關研究聚焦于智能體的收益函數的設計和博弈決策方法上.收益函數的設計很大程度影響了博弈優化的收斂效果,為了保證系統能在多輪博弈后達到納什均衡,常見的做法是根據實際情況將收益函數設計成符合勢博弈(potential games)[7]和凸博弈(convex games)[8]等具有良好收斂性質的形式.Li等人[9]通過改造系統的全局目標函數作為各個智能體的收益函數,設計了一種使用非完全信息的勢博弈分布式優化模型;Wu等人[10]為多智能體任務分配問題設計了一種勢博弈模型,該模型將各智能體的收益函數設置為任務收益的指數形式,保證重要的任務被優先完成,此外,將實際需求與參與智能體數目之差作為指數,防止過多的智能體被分配于同一任務造成浪費.博弈決策的目的是如何讓智能體做出決策優化自身收益函數的值,常見的決策方法有沿收益函數的梯度調整的梯度博弈(gradient-play)[11]、根據歷史博弈記錄計算最佳決策的虛擬博弈(fictitious play)[12]、根據概率分布選擇策略的對數線性學習(log-linear learning)[13]等.Ye等人[14]對梯度博弈進行了擴展,在收益函數中使用對所有智能體值的估計值計算梯度,使其能讓系統中的各個智能體在不了解全局信息的情況下收斂至納什均衡;Heinrich等人[15]使用強化學習過程尋找最優近似代替虛擬博弈中的最優策略選取,改善了此類方法在大規模的博弈場景中的表現.
在分布式多智能體博弈中,智能體之間的信念沖突是導致博弈無法達到納什均衡的主要原因之一,本文采用多智能體一致性協議(consensus protocols)緩解系統中各個智能體之間的信念差異,該技術來源于自動化和控制理論領域,是一種通過智能體間信息交換實現信念趨同和協同合作的技術.Saber等人在文獻[16]中提出了多智能體一致性協議的基礎形式和收斂分析,并在文獻[17]中進一步分析了收斂速度與智能體網絡的連通度和網絡類型之間的關系;Xie等人[18]在基礎的一致性協議上增加了基于智能體當前狀態的反饋控制機制,該協議能在變化的網絡連接狀態下收斂;Zuo等人[19]根據不等式關系進一步改造了一致性協議,使其能在有外部干擾的情況下以任意初始狀態在有限時間內收斂.
2 優化模型
2.1 系統模型
為了便于讀者理解本文的優化決策機制,首先給出本文的系統模型.本文系統模型的構建基于廣泛應用于自主計算領域的感知—分析—決策—執行(monitor-analyze-plan-execute, MAPE)控制方法[20],如圖1所示,MAPE循環包括4個主要階段:
1) 感知(monitor)階段.該階段收集系統信息,對系統參數和結構的變化情況進行監控,并將變化數值化傳遞給分析階段.
2) 分析(analyze)階段.該階段根據感知階段收集的信息確定系統的當前狀態和變化趨勢.
3) 決策(plan)階段.該階段針對當前系統的狀態和問題產生調整策略,以保證系統的穩定運行或優化系統的性能.
4) 執行(execute)階段.該階段根據決策階段產生的策略調整系統行為,在執行階段結束后,將再次進入感知階段開啟下輪MAPE控制循環.

Fig. 1 MAPE loop圖1 MAPE循環
本文的系統模型如圖2所示,在網絡化軟件系統中設置分析預測節點負責感知階段和分析階段的工作,收集節點信息,分析預測節點根據與軟件節點間的網絡延遲確定管理范圍,對分析范圍內的軟件系統狀態建模并分析預測系統性能的變化情況,生成節點數據與該區域系統總體效益之間的函數[21].分析完成后,各個分析預測節點將結果分發給網絡中的軟件節點,部署在各個軟件節點上的智能體以此為依據對節點的參數進行調整,實現系統性能的整體優化.

Fig. 2 System model of networked software圖2 網絡化軟件系統模型
在這個過程中,由于網絡化軟件系統的性能受各個軟件節點狀態的影響,分析預測節點得到的函數變量中包含多個軟件節點的參數,部署在軟件節點上的智能體需要擁有其他節點的信息才能做出優化決策.然而,分布在各處的軟件節點雖然能夠通過網絡相互通信間接獲取全局的節點信息,但長距離通信的延遲和不穩定會導致信息傳遞緩慢,進而影響優化決策的效率,該問題會隨軟件部署的規模擴大而加深.因此本文讓每個節點通過不完全的節點信息,相互博弈做出決策,具體做法是根據每次優化的最大時間限制和迭代次數上限計算出通信時延的閾值,各個節點選擇與自己通信穩定且通信時延較符合閾值的節點建立連接,智能體使用不完全的節點信息做出決策來優化軟件性能.
2.2 博弈模型
本文的主要研究內容是通過分布在軟件節點上智能體間的博弈實現網絡化軟件優化機制,一個博弈場景G描述為G={N,v,V,F,J},下面分別介紹.
1)N={A1,A2,…,An}為網絡中的智能體集合,其中n為集合的大小,即網絡化軟件的節點數量.
2)v=(v1,v2,…,vn),其中vi為各個智能體維護的取值(value),取值可以代表節點的最大硬件負載、最大任務排隊量等參數,智能體通過調整自身的取值實現各類優化決策.
3)V=V1×V2×…×Vn,其中Vi為各個智能體的取值空間(value space),取值空間是對智能體取值的限制,對于每個智能體的值有vi∈Vi,即智能體只能在取值空間規定的范圍內調整自身的取值.
4)F:V為全局效益函數,是一個關于智能體取值的函數,由所有分析預測節點根據系統的情況給出,用于衡量系統的整體性能.本文中的效益函數F的結果為系統功耗、響應時間等與軟件系統性能負相關的指標,系統的優化目標等價于優化問題:
(1)
5)J={J1,J2,…,Jn}為各個智能體的收益函數集合,其中Ji:V,收益函數由分析預測節點賦予智能體,是智能體進行決策的標準,各個智能體在多輪博弈中通過調整自身取值獲取更高的收益函數值,并最終讓整個系統達到納什均衡(Nash equilibrium),從而產生調整策略,納什均衡的定義如下.


在納什均衡下,網絡中所有的智能體都無法僅通過改變自身的取值使得自身的收益函數結果變得更好,當博弈到達納什均衡時,各個智能體的取值將趨于穩定.通過合理地構造智能體的收益函數,可以讓博弈的納什均衡充分接近如式(1)所示的優化問題的解.本文使用一種簡單的博弈構造方法,對于網絡中的所有智能體Ai,令
這種方式構造出的是一類具有良好特性的博弈:勢博弈(potential games).

則稱博弈G為勢博弈,Φ為G的勢函數.
顯然,使用上文方法構造出的全局效益函數F是對應博弈的勢函數.在勢博弈中,單個智能體的取值改變對其自身的收益函數的影響和對全局效益函數的影響相同,有限勢博弈一定存在納什均衡,這為本文的優化決策設計提供了收斂保證.由于各個智能體不能完全掌握網絡中所有智能體的取值情況,所以無法直接計算收益函數.為了解決這個問題,引入智能體的取值估計(estimation)[9]:e=(e1,e2,…,en)替代真實的取值計算收益函數,其中ei= (ei1,ei2,…,ein),eij表示智能體Ai對智能體Aj取值的估計,用于替代智能體Ai可能無法得知的智能體Aj的取值vj.在第3節中將介紹如何讓取值估計在博弈迭代過程中接近各個智能體的真實取值,以使得這種決策方式是有效的.
3 網絡化軟件博弈優化機制
3.1 基于多智能體一致性的梯度博弈
本文考慮連續博弈(continuous games),即F和Ji均為連續函數的博弈決策問題,如帶寬控制等采用連續取值空間的優化問題需要使用連續博弈解決,服務降級、CPU核心、成塊的內存分配等離散目標則需要先轉換為連續的優化問題.梯度博弈是一種常用的連續博弈決策方法[23],在每輪博弈中,各個智能體將取值估計代入收益函數,沿自身取值的梯度方向對取值進行調整:
(2)
其中:vi(t)表示智能體Ai在第t輪迭代時的取值;εi>0,為每輪更新取值的步長;符號[·]+表示第t輪時梯度在智能體Ai可選取值變化集合上的投影,防止取值超出該節點可以選擇的范圍.對于第2節中構造的博弈G={N,v,V,F,J},設F在V上具有凸性,則G能使用梯度博弈以合適的步長收斂至納什均衡[9,23],大部分的軟件優化問題滿足該條件或可轉化為滿足該條件的等價問題[24-25],如果無法滿足該條件則無法使用此類方法求解納什均衡.與常規的梯度博弈不同,式(2)在更新取值時使用的不是真實的梯度,而是根據估計值ei計算出的虛擬梯度,顯然,如果在博弈迭代中智能體無法正確估計全局的取值情況,梯度博弈將由于錯誤的梯度而無法收斂至納什均衡.
為了讓智能體正確估計其余智能體的取值,基于一致性協議對各個智能體的估計值進行修正,使其接近系統中各個節點的真實狀態.在每輪博弈的取值調整前,每個智能體向與其建立連接的智能體集合Ni發送自己的取值和估計信息,并在調整結束后利用這些信息:
1) 通過一致性協議[16]減少各個智能體之間的估計誤差,令
(3)
其中Ni為與Ai建立連接的智能體集合(包括Ai自身).

(4)
注意,雖然每個智能體能在博弈當中獲取一定的真實取值信息,但不能通過持續將其代入收益函數的方式計算梯度,因為這樣會破壞式(3)的信息交換,可能會引起算法失效.
3) 更新估計值
(5)
其中α1和α2為比例系數,0<α1<1,0<α2<1,α1和α2用于約束估計值的變化速度.與常規的一致性協議不同,以上方法中除了需要讓智能體與相鄰智能體的估計趨于一致外,還要讓估計值接近一組不斷變化的真實取值.
綜合第2節中的系統模型和本節的博弈機制,基于Li等人[9]和Ye等人[14]的工作,我們總結了基于多智能體一致性和梯度博弈的分布式優化(distributed optimization based on consensus and gradient-play, DOCG)算法.
算法1.DOCG算法.
輸入:迭代次數上限l、各個智能體的初始取值vi(0)、梯度博弈步長εi、比例系數α1和α2;
輸出:更新完成后的各個智能體取值v′.
① for each AgentIinN
②ei(0)←v(0);/*通過網絡通信初始化各
個智能體的估計值*/
③ end for
④iter_count←0;
⑤ whileiter_count ⑥ for each AgentIinN ⑦getinfo(); /*從相鄰的智能體獲取信息*/ ⑧gradient_play(ei(iter_count),εi); /*使用估計值和梯度博弈更新取值*/ ⑨estimation_update();/*基于相鄰智 能體的信息更新估計值*/ ⑩ end for 顯然,智能體間到達納什均衡的充要條件為所有智能體的估計值等于其可獲得的真實取值,且在多輪迭代中不再變化.當智能體的估計值與相鄰智能體取值相等且穩定時,根據梯度博弈的原理,任何智能體對取值做出的調整都會讓自身的收益函數結果變差,根據定義1,此時博弈已達到納什均衡;另一方面,假設存在智能體的估計值與相鄰智能體的估計或真實取值序列存在偏差,那么在接下來的迭代中該智能體仍會根據式(5)修正自身的估計值,此時智能體間并不是納什均衡狀態.基于Ye等人[14]的分析,在效益函數滿足一定條件時,使用算法1控制的系統達到的納什均衡是Lyapunov穩定的,軟件系統本質上也是一種控制系統[26],但算法1中的梯度博弈的步長和估計修正中的比例系數很大程度上影響了方法的收斂能力.在3.2節和3.3節中,將探究如何設置和控制這2類參數以提升算法的收斂能力. 在算法1中,取值更新和估計修正過程是相互影響的,過大的估計誤差會造成梯度方向的偏移,使取值越來越偏離應有的更新方向,同時取值的錯誤更新也會反作用于估計值的修正,進而造成惡性循環讓取值點“迷失”在高維曲面上無法到達對應納什均衡的取值點.對于更新步長ε=(εi)和比例系數α1,α2各存在一組范圍上限,當ε和α1,α2均在范圍限制之內時,算法1能保證收斂至納什均衡,但這2類上限的嚴格計算都和全局效益函數F有關,且對于每個智能體,計算這2類上限的時間復雜度均在O(n2)以上[14].顯然通過計算確定這2種參數是不明智的,而為了保證方法收斂保守地選擇參數則會降低算法的效率. 對于算法1,假設比例系數符合收斂限制,暫時停止取值的更新(暫時令步長ε=0)并讓各個智能體以式(5)的方法修正估計值,各個智能體的估計值將在迭代中逐漸統一并收斂于真實的取值.這時使用式(2)計算的梯度將趨于真實的梯度,之后當估計誤差過大時再次停止更新取值并修正估計值,重復這個過程能讓各個智能體將取值調整至納什均衡的某個鄰域當中,但這種做法會大幅降低算法的效率.基于以上討論,我們提出一種隨迭代過程變化的步長選取方法,令 (6) 其中 為智能體估計值與相鄰智能體真實取值之間的誤差;εmax i為該智能體沿虛擬梯度更新的最大步長,當智能體對相鄰智能體的估計值沒有誤差時,可以以最大步長更新自身的取值;τi為衰減系數,0<τi<1,讓取值的迭代步長隨估計誤差的增大而減小,實現在誤差過大時減緩取值的更新速度. 可變步長可以防止上文中提到的“取值迷失”情況并為步長提供了更大的選擇空間,但同時也帶來了新的問題.在算法執行后期各個智能體之間的估計值和取值差異將逐步收斂,此時可變步長也將趨于最大步長,如圖3所示,當最大步長過大時算法會在納什均衡點附近發生震蕩,這種現象會隨著最大步長的增加而變得越發嚴重.根據3.1節中關于算法1的納什均衡條件的討論,當震蕩現象發生時降低最大步長即可讓算法收斂,具體做法為:為式(3)的估計誤差設定范圍判斷其是否接近收斂狀態,在幾輪迭代后,若估計誤差接近算法卻沒有達到納什均衡,則逐步下調最大步長,該機制的具體執行方式見3.4節. Fig. 3 Oscillation phenomenon圖3 震蕩現象 3.2節中,我們在比例系數符合收斂條件的情況下討論了步長的設計與調整,然而,不當的比例系數將導致估計值與真實取值之間的誤差越來越大,讓式(6)的可變步長逐漸趨于0,最終智能體的取值不再更新,算法呈現出如圖4所示的過早收斂現象. Fig. 4 Premature convergence phenomenon圖4 過早收斂現象 為了防止因不當的比例系數引起的算法過早收斂,我們為基于可變步長的算法1研究一種比例系數調整和誤差協調機制.類似于3.2節中的最大步長調整方法,為智能體的可變步長設置下限δε,當可變步長小于δε時,觸發強制協調: 1) 由于舊的比例系數無法有效地修正估計值,首先需要嘗試降低當前的比例系數,讓比例系數以某種方式降低,比例系數降低后,誤差的擴大速度將減慢,如果此時的比例系數仍會引起過早收斂,使用原先的判斷條件觸發強制協調需要更多的迭代輪數,需要更加嚴格地對誤差大小進行限制,合理地提高判斷誤差過大的可變步長下限δε; 2) 另一方面,觸發強制協調機制時各個智能體的估計誤差很大,考慮到使用式(5)的迭代方法修正誤差的效率,且調整后的比例系數可能仍不符合收斂條件,會繼續擴大誤差,因此在觸發強制協調時將各個智能體當前可獲得的取值信息賦值于其估計值,即讓 eij=vj,Aj∈Nj. 強制協調完成后,智能體繼續執行算法直至發現誤差過大再次進行協調或達到納什均衡.強制協調的本質是限制智能體之間估計誤差的大小并在必要時修正比例系數和重啟算法,提高收斂速度. 將3.2節中的自適應步長機制和強制協調機制綜合到算法1中,本文的網絡化軟件優化決策機制可以總結為算法2. 算法2.DOCGAC(distributed optimization based on consensus and gradient-play with adaptive step size and coordination)算法. 輸入:迭代次數上限l、各個智能體的初始取值vi(0)、最大步長εmax i、衰減系數τi、初始比例系數α1和α2、判別震蕩的估計誤差范圍δerr、判別過早收斂的可變步長下限δε; 輸出:更新完成后的各個智能體取值v′. ① for each AgentIinN ②ei(0)←v(0); ③ end for ④iter_count←0; ⑤ whileiter_count ⑥ for each AgentIinN ⑦getinfo(); ⑧εi←variable_step_size(ei(iter_count), {vj(iter_count)},εmax i,τi) ; /*可變步長*/ ⑨gradient_play(vi(iter_count), ei(iter_count),εi); ⑩estimation_update();/*更新估計值*/ 算法2使用了按比例減小的方法搜索合適的參數.在最大步長和比例系數的下調方面,只要讓它們進入收斂條件的范圍即可,保守的下調可能導致頻繁觸發調整機制,而過于激進的下調方式反而會讓參數變得過小影響方法的收斂速度,甚至引起類似于提前收斂的情況,按比例縮小是一種較為折中的選擇.另一方面,合理的初始值能夠減少參數下調觸發的次數,提高算法的收斂速度.對于最大步長,其合理的初始取值受網絡規模和效益函數的復雜程度影響,在實際使用中,由于系統在運行過程中會多次執行優化機制,因此可以根據同類型優化問題處理時的歷史數據對初始值進行調整,如果智能體在連續的r輪迭代中都未觸發步長下調,則可以謹慎地提高初始值以提高算法的收斂速度,更新最大步長為 其中β為大于1的數,可以選用下調最大步長時使用乘數的倒數,反之,如果在1輪算法中需要多次下調步長,則需要在下次算法開始前降低初始值.智能體在執行算法時記錄本次算法中觸發下調最大步長的次數c,令新的最大步長為 最大步長會在長期的優化過程中趨于穩定.對于比例系數α1,α1限制的是式(3)中基于一致性協議的估計修正速率,該值與智能體的相鄰智能體個數有關,相鄰智能體的個數越多,誤差的累積效應就越強,一種簡單的選取方法是讓每個智能體的初始比例系數α1與其鄰接智能體的個數成反比,如令 (7) 而α2限制的式(4)只和單個相鄰智能體的取值有關,其本質是估計值向取值的靠近速度,與梯度博弈中的步長類似,因此可讓其初始值與最大步長的初始值保持一致. 為了驗證方法的有效性,我們將在4.1節和4.2節對本團隊前期開發的網上商城系統[27]進行了仿真實驗,該軟件是典型的互聯網應用,通過集群節點協同為用戶提供服務,其整體性能受各個節點的狀態影響,適合使用本文的方法進行調控.我們基于團隊在軟件狀態分析方面的工作[21]分析了該系統某一時段的各個節點帶寬與總體響應延遲之間的關系,建立了模擬該系統的10個虛擬節點,以圖5所示的方式進行連接,通過本文提出的方法讓各個智能體調節軟件節點的帶寬,以系統響應時間的預測值為指標方法驗證有效性,初始帶寬的取值使用了分析時的日志記錄值. Fig. 5 Connectivity of agents in our simulation圖5 本文仿真實驗智能體連接方式 在本節中,我們對3.2節和3.3節提出的2類機制觸發和效果分別進行了測試,以驗證它們的效果. 1) 自適應梯度步長機制的觸發 本文的自適應梯度步長機制分為可變步長和最大步長的調整過程,本節分別對完整的自適應梯度步長機制、只使用可變步長以及只使用最大步長下調的情況進行了實驗,實驗結果分別如圖6所示.本輪實驗中,各個智能體的最大步長εmax i均取0.3,衰減系數τi均取0.5,比例系數α1,α2均分別取0.2,0.4,其中,在只使用最大步長下調的情況下使用的最大步長為0.1. Fig. 6 Triggering of adaptive step size mechanism圖6 自適應步長機制的觸發情況 從圖6中可以看出,如果不使用步長下調,算法會在即將到達納什均衡時由于過大的步長發生震蕩現象;如果不使用可變步長,算法雖然能在合適的步長下收斂至納什均衡,但在收斂過程中會受到估計誤差的影響,出現頻繁的震動,此時比例系數稍有不當就會讓估計值與真實值的誤差越來越大進而導致算法發散. 2) 強制協調機制 Fig. 7 Triggering of forced coordination mechanism圖7 強制協調機制的觸發情況 我們首先測試了在使用可變步長時強制協調機制的觸發情況,分別對使用和不使用強制協調下的方法迭代情況進行了實驗測試.令所有智能體的初始最大步長εmax i=0.2,衰減系數τi=0.5,比例系數α1的初始值按式(7)的方法選取,α2的初始值均取0.8,實驗結果如圖7(a)所示.在不使用強制協調的情況下,由于估計誤差過大可變步長歸零導致算法在迭代剛剛開始時就停止更新,而強制協調機制能夠對比例系數進行搜索并有效避免過早收斂現象.另一方面,不使用可變步長,在步長合適的情況下,使用強制協調機制也能實現對比例系數的搜索.如圖7(b)所示,將所有智能體的步長均固定為0.1,用于判斷估計誤差大小的最大步長設置為0.08(雖然不使用可變步長,但強制協調機制的觸發條件是該值的大小,本輪實驗中的可變步長僅用于判斷估計誤差大小,不用于計算取值更新),算法在經過幾次比例系數的下調后成功收斂到納什均衡,相同的參數選取下不使用強制協調機制算法會發散. 根據4.1節的討論,算法2主要在收斂速度、參數選取等方面對算法1進行了改進,我們分別使用算法1和算法2對本節開始時提到的優化問題進行了處理,同時,為了進一步驗證本文方法相較于傳統方法的優勢,我們選取了經典的最佳響應(best response, BR)和虛擬博弈 (fictitious play, FP)[12]作為參照.BR,FP以及本文使用的梯度方法是機器博弈研究中3類常見的決策方法,當前該領域的研究大多是在這3類方法的基礎上改進而來,目前仍有很多相關的研究和討論,其中最主要的研究是通過近似值替代最佳值的方式克服大量數據帶來的求解問題[15,28-29],在本文的實驗條件下近似值會影響求解精度和收斂輪數,此處使用精確的最佳值反映3種方法間的區別以及不完全信息帶來的影響.本輪實驗中,算法1的參數選取:為了防止發散,步長εi均使用0.05,比例系數α1,α2均分別設定為0.2,0.8;算法2的參數選取:初始最大步長εmax i均設置為表現較為平均的0.3,衰減系數τi均使用較為保守的0.5,比例系數α1的初始值使用式(7)的選取方法,α2的初始值均設置為0.8;BR和FP均使用估計值計算收益函數,為了確保能夠順利執行,這2種算法的比例系數組合都選取為0.2和0.3. Fig. 8 Convergence performance of algorithms圖8 各類算法的效果對比 實驗結果如圖8所示,可以看出算法1使用較為保守的參數平穩地收斂到納什均衡,而算法2由于在執行初期更新取值時使用了最大步長,各個智能體間的博弈導致預期結果發生了巨大的波動,但在接下來的幾輪博弈中在可變步長和強制協調機制的控制下,各個智能體放慢了更新幅度并修正了自身對其他智能體的估計,將取值更新重新拉回了正確的方向,最后比改進前的算法更快速地收斂到了納什均衡.BR由于各個智能體激進地追求自身的最佳收益,無法完全達成平衡;FP通過根據歷史平均采取最佳響應,穩定地收斂到了平衡狀態,但收斂速度不如前2種方法. 為了驗證方法在復雜網絡中的效果,我們進行了更大規模的實驗,設置了1 000個模擬節點.由于可供使用的節點數據不足,我們模仿文獻[14]中的方法進行了數值實驗,在3種典型的網絡結構:隨機網絡、小世界網絡、無標度網絡上對算法2進行了測試.在隨機網絡中設置連邊概率p分別為0.1,0.2,0.4,0.8;在小世界網絡中,鄰邊數k分別取20,40,80,100,重連概率被固定為0.2;在無標度網絡中,每次加入的邊數m分別設置為10,20,40,50,每種網絡隨機生成后進行測試記錄結果,各重復20次取平均值,實驗結果如圖9所示.由圖9可知,在隨機網絡中,隨著智能體間的連邊增加,算法的收斂速度會大幅減慢,但不會引起發散.這與我們的設想相反,因為一致性協議修正估計值的速度會隨連邊的增加而加快[17],且在全連接實驗中,算法的收斂表現非常好.引起這種情況的原因是復雜的網絡構成讓智能體間的估計相互影響,導致估計修正速度變慢,進而減慢了達到納什均衡的速度.而在小世界網絡和無標度網絡中,由于在局部的網絡結構中出現了近似于全連接的狀態,降低了該問題的影響,因此在這2種網絡中,連邊數量的增加對收斂性能的影響不大.網絡的復雜性會一定程度上降低算法的收斂效率,但不會導致算法失效. Fig. 9 Experimental results of algorithm in complex networks圖9 復雜網絡的算法實驗結果 在本文中,我們針對網絡化軟件的優化決策問題建立了系統模型,將現有的基于多智能體一致性的分布式梯度博弈方法研究總結為了DOCG算法,并提出了將其應用在網絡化軟件的優化決策問題中的方法.此外,我們對該算法進行了改進,研究了能調節尋優速度和自動搜索合適參數的自適應步長機制和強制協調機制,提出了DOCGAC算法,為軟件在連續工作中的持續參數優化提供了一種解決方案.實驗結果表明,改進后的算法能更快地收斂至納什均衡,并且降低了方法對參數選取的要求,使此類算法能夠應用于網絡化軟件系統的優化任務中. 我們的方法也存在一定的不足,與原算法相同,DOCGAC收斂到的納什均衡無法保證是對應優化問題的全局最優解.在未來的工作中,我們將探索如何讓此類方法的納什均衡更靠近理論最優值,并在真實的大規模網絡化軟件中進一步測試和改進我們的方法. 作者貢獻聲明:舒暢提出核心方法,參與實驗框架的設計和實驗編程,并最終完成了論文的撰寫;李青山擬定研究方向,設計了具體的研究方案;王璐設計了實驗框架和方法,完善研究方案;王子奇負責實驗編程及論文撰寫;計亞江負責實驗數據收集和論文核定.3.2 自適應梯度步長機制

3.3 強制協調機制

3.4 決策算法
4 實驗分析

4.1 機制觸發
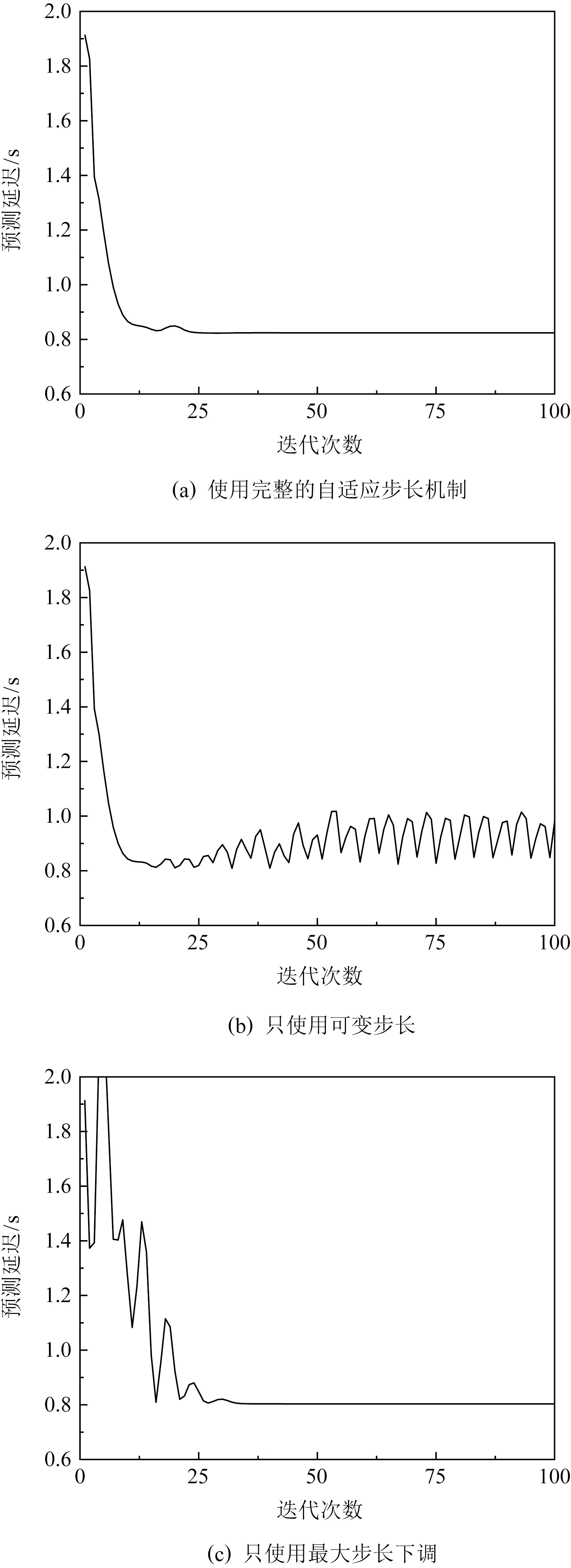

4.2 對比實驗

4.3 復雜網絡實驗

5 總結與展望

