含海上風電?光伏?儲能的多能源發輸電系統可靠性評估

高小童，秦志龍，高新宇

（1. 山東省調水工程運行維護中心棘洪灘水庫管理站，山東省 青島市266111；2. 國網青島供電公司，山東省 青島市266002；3. 合肥工業大學電氣與自動化工程學院，安徽省 合肥市230009）

0 引言

因地制宜發展光伏發電、風電等可再生能源，建設風光儲一體化基地是我國貫徹落實碳達峰、碳中和戰略目標的重要途徑。然而，風能和太陽能的間歇性和不確定性給電網安全可靠運行帶來風險[1-3]。目前，儲能可作為一種成熟技術用來平抑間歇性能源發電功率的頻繁波動，提高電網的可靠性水平[4-5]。我國缺乏常規能源的東部沿海地區大多處于用電負荷中心，附近海域常年風能資源豐富，大力建設海上風電場是發展趨勢。海上風電未來將成為緩解我國東部地區電力供需壓力的重要途徑。海上風電與光伏、儲能等多種能源的綜合開發利用和融合發展，也將是未來海上風電的重要發展方向。多個海上風電場、光伏電站及儲能電站聯合系統接入城市電網時，勢必會對電網的供電可靠性產生積極的影響。在評估電網可靠性影響時，如何準確地模擬風電場功率、光伏電站功率和電網負荷是系統可靠性評估的基礎。

近年來，國內外專家對風光儲聯合系統的可靠性評估進行了大量研究[6-9]。如：文獻[6]針對風、光資源的分布特點，結合發電系統設備的運行狀態，建立了含風力、光伏、儲能的發電系統可靠性數學模型，在風光儲不同的協調運行方式下，對含風光儲的發電系統進行了可靠性評估。文獻[7]根據電力系統實際負荷數據，分別對只含常規機組、風電并網以及儲能參與高比例風電并網3 個不同場景下的電力系統進行了可靠性指標計算，分析了儲能系統對電力系統可靠運行的積極影響。文獻[8]建立了風電機組功率時序模型和含風電場?儲能發電系統可靠性評估模型，并結合常規機組的狀態模型，建立了基于序貫蒙特卡羅仿真的含風電?儲能發電系統可靠性模型，量化儲能系統和風電場接入發電系統的可靠性影響。文獻[9]提出一種兼顧可靠性、靈活性和經濟性的風光儲虛擬電廠分層容量配置策略，以提升系統的可靠性水平和經濟效益。然而，以上研究均未考慮新能源功率之間、新能源功率與電網負荷之間的相關特性，以及惡劣天氣對風電場的影響等因素，不能客觀地反映真實系統可靠性水平。

同一區域的風電場功率、光伏電站功率和電網負荷三者之間也存在或正或負的相關結構，如果忽略這種相關性，就會產生較大的系統可靠性評估誤差[10]。相比于陸上風電場，海上風電場及其附屬并網系統易受海上惡劣天氣的影響，其故障率高以及維修時間長的特點凸顯，傳統可靠性評估模型誤差較大，需考慮惡劣天氣對海上風電場及柔性直流并網系統可靠性評估的影響[11]。綜上所述，為了準確地建立風電場功率、光伏電站功率和電網負荷三者聯合系統的可靠性模型，需要綜合計入風電場功率、光伏電站功率和電網負荷三者的相關性，以及惡劣天氣對海上風電場風機及其柔性直流并網系統隨機故障率的影響等因素。

在描述風電場功率、光伏電站功率和電網負荷間相關結構方面，由于Copula 函數可以完整地描述多變量間的相關結構，尤其在刻畫非線性相關性方面存在明顯優勢[12]，被越來越廣泛地應用到相依結構分析等領域。常用的Copula 函數雖然可以擴展到高維形式，但表達式往往非常復雜，不利于在高維情景中的應用；并且假設兩兩變量間具有一致相依結構，如果用同一函數表達此相依結構，則存在明顯的不足。已有研究用單一靜態Copula 函數[13]、單一時變Copula 函數[14-15]、混合靜態Copula 函數[16-17]、混合時變Copula 函數[18]、基于藤結構的單一靜態Copula 函數[19]、基于藤結構的混合靜態Copula 函數[20]探索多個風電場功率間的相關性，以及風電場與光伏電站功率間的相關性，但均未能有效地刻畫這些新能源功率間隱藏的相關性，而且也沒有描述這些新能源與電網負荷間的相關結構。

本文基于C 藤的多元Pair-Copula 結構，構建混合時變Copula 模型，以描述光伏功率、風電功率、電網負荷間的多元相關結構，并建立8 種風光荷聯合Copula模型，運用赤池信息準則(Akaike information criterion，AIC)和貝葉斯信息準則(Bayesian information criterion，BIC)選擇出最優模型，同時建立風速和雷擊對風機失效率影響的時變分析模型，以及惡劣天氣對元件修復時間影響的時變模型。最后，把8 種模型應用到含風電場、光伏電站、儲能電站的發輸電系統可靠性評估中，以驗證所提相關性模型的可行性與有效性。

1 基于藤結構的混合時變Copula模型

1.1 藤Copula模型

藤Copula函數是近年來Copula理論中取得的較新進展，它建立在簡單二元Copula 函數基礎上，能聯合考慮高維變量間的相依結構。藤Copula 模型可將多維變量的相依結構分解為多個二維相關變量，常用的有C 藤和D 藤結構，兩者因邏輯結構不同，其適用的數據類型也有所差別[19-20]。結合實際風電場功率、光伏電站功率、電網負荷間的相關性分析，本文采用C 藤結構進行研究分析。C藤模型具有星型結構，如圖1所示。

圖1 C藤結構邏輯圖Fig.1 Logic diagram of C-vine structure

按照C-Vine 結構分解的n維變量，聯合概率分布表達式如下：

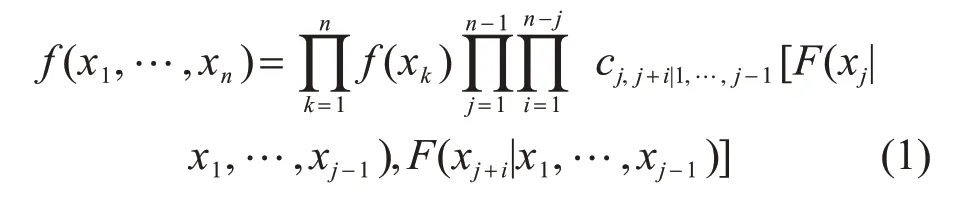
式中：xk為第k維變量；f(xk)為xk的概率密度函數；F(xj)為xj的累積分布函數；c(·)為Copula 密度函數。

式(1)中條件分析具備以下性質：

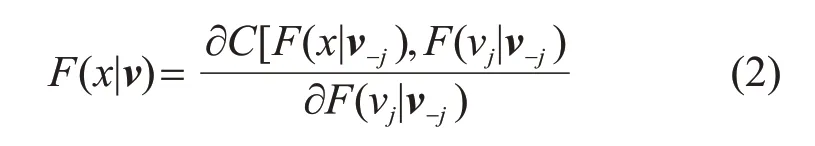
式中：vj為n維向量v中的第j個變量；v-j為向量v去掉vj的n?1維向量；C(·)為二元Copula分布函數。

1.2 時變相關Copula模型

風電場功率、光伏電站功率、電網負荷總是時刻變化的，三者間的相關特性也不是一成不變的，兩兩之間或呈正相關特性，或呈負相關特性，在一定的時間周期內必然存在一個相關性的變化，因此需通過時變相關Copula 模型來描述變量間非線性時變相依結構[14-15]。常用的相關Copula 模型主要有時變t-Copula 函數、時變Rotated Gumbel Copula(RG-Copula)函數、時變Symmetrized Joe-Clayton Copula(SJC-Copula)函數[14-15]。

1）時變t-Copula函數

二維時變t-Copula函數的分布函數表達式為

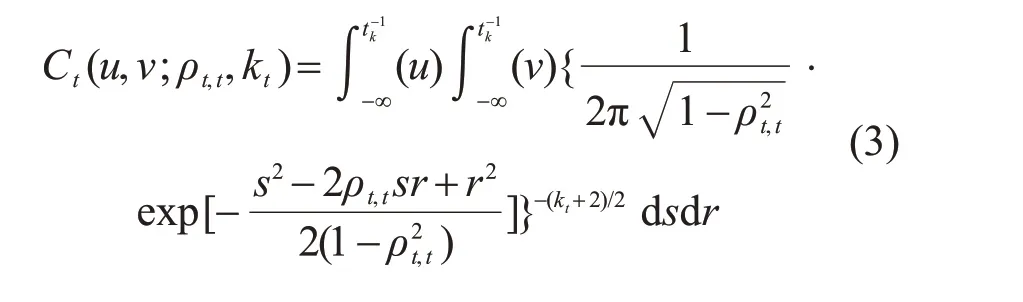
式中：s、r為隨機變量；u、v為邊緣分布函數；ρt,t為時變相關系數；kt為自由度；t-1k為自由度下的t分布逆函數。

根據DCC(1,1)，t-Copula的相關系數矩陣可分解為：

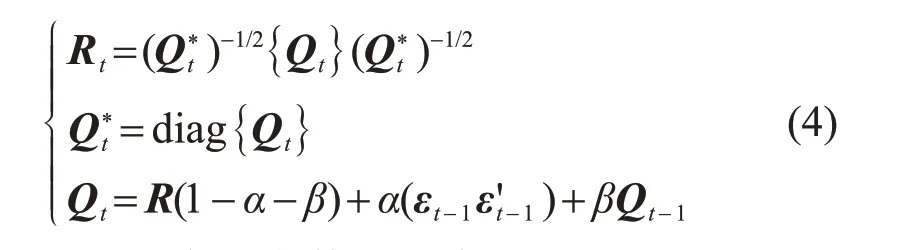
式中：α、β是未知參數，且滿足0<α<1，0<β<1，0<α+β<1；Qt必須正定；εt-1為分布函數的偽逆函數序列。時變t-Copula 函數在表達對稱的尾部關系方面比較有優勢。

2）時變RG-Copula函數

時變RG-Copula函數的分布函數表達式為

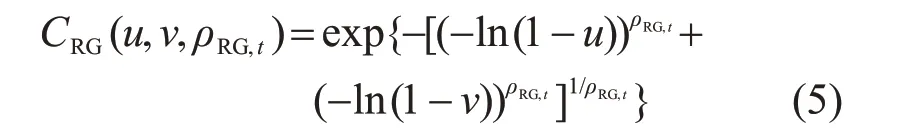
其中時變系數

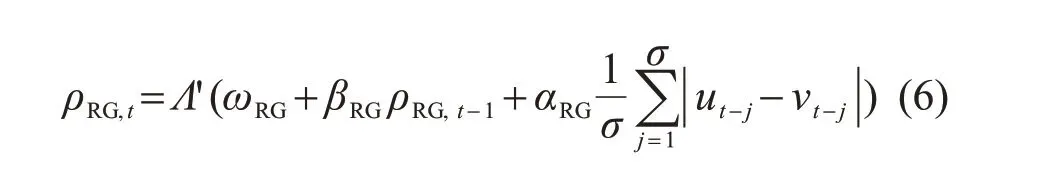
式中：logistic 變換函數Λ'(x)=1+x2，確保時變系數ρRG,t>1；ωRG、αRG、βRG為時變方程參數；數據窗口σ一般情況下取10[14]，下同。

時變RG-Copula函數上尾相關系數為0，下尾相關系數為

3）時變SJC-Copula函數

時變SJC-Copula函數的分布函數表達式為

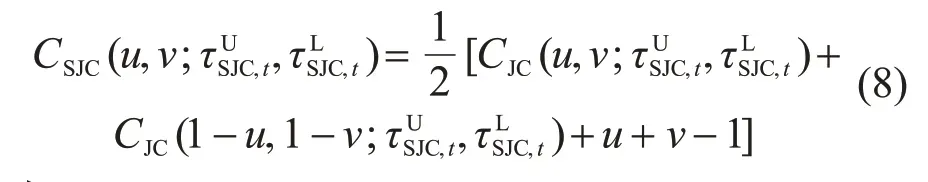
其中：

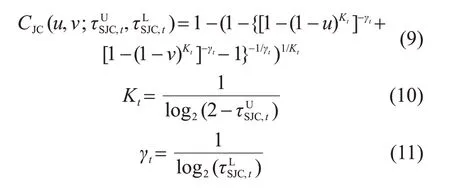
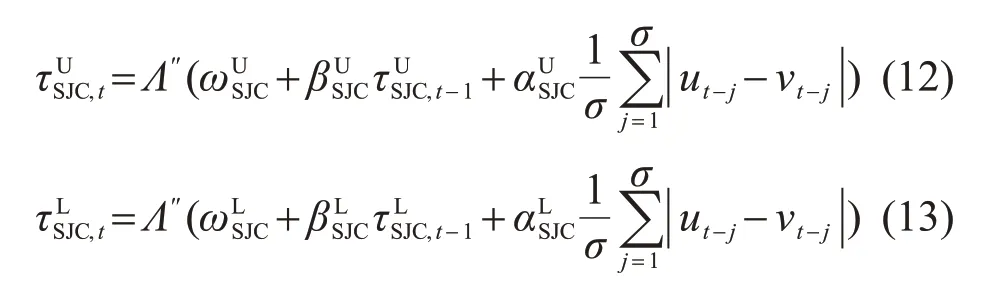
式中：logistic 變換函數Λ''(x)=(1+e-x)-1，確保上下尾相關系數都在(0, 1)范圍內；為上尾時變方程參數；為下尾時變方程參數。時變SJC-Copula 函數可以較好地刻畫上、下尾相關特性[14]。

1.3 混合時變Copula模型

由1.2節可知，不同的時變Copula函數在描述變量間相關性時各具特點，在實際應用中，如果用某一種時變Copula 函數去精準刻畫類型多樣、時變、非線性的風光荷相關性特征，顯然是不合適的。將這幾類單一時變Copula 函數通過一定的方式進行組合，構建一個混合時變Copula函數[17]，不僅可以描述風光荷間的上尾相關、下尾相關和尾部對稱相關3種相關模式，還可以通過選取不同的權重來描述三者之間上尾相關、下尾相關并存的非對稱相關模式。因此，在刻畫復雜多變的風光荷相關結構方面，混合時變Copula 函數比單一時變Copula函數更加有優勢。混合后的Copula函數[17]表示為

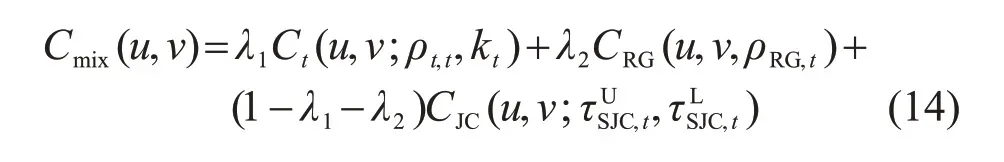
式中λ1、λ2為權重系數，滿足0≤λ1≤1，0≤λ2≤1。

式(14)中的時變參數和權重參數可通過期望最大化(expectation-maximum，EM)算法[21]估算出。

1.4 基于藤結構的混合時變Copula 模型構建及參數估計

雖然利用混合時變Copula 函數分析二維變量之間的相關性可以獲得不錯的分析結果，但是當變量維數上升至三維時，其分析結果的精度明顯變差。為解決高維Copula 函數建模時的維數災和準確性問題，藤結構方法的思路是把多個變量之間的相關性逐步分解成多個二維變量之間兩兩相關性，即將高維Copula 函數的求解轉換成多個二維Copula函數的求解，有效避免了維數災。

模型構建及參數估計過程如下：

1）利用非參數核密度分布函數[7]將風電場功率、光伏電站功率和電網負荷樣本轉換為服從[0,1]均勻分布的時序數據，作為構建模型的初始點，即C藤結構中樹T1的觀測值；

2）計算風?光?荷變量兩兩間秩相關系數η[22]，并確定第一棵樹上的變量排列順序；

3）對于樹Tj的每一條邊i(i=1,…,n-j)，構建混合時變Copula 模型，通過EM 算法估算出式(14)中未知參數；

4）利用Tj估計出來的混合時變Copula 模型以及式(2)計算出下一棵樹Tj+1的觀測值；

5）重復步驟3）、4），直到最后一棵樹j=n?1。

1.5 Copula 模型選擇評價準則

為了驗證本文所提出Copula 模型的有效性，通過2 個廣泛使用的評價準則AIC 和BIC 來選擇最優的Copula模型，其值分別表示如下：

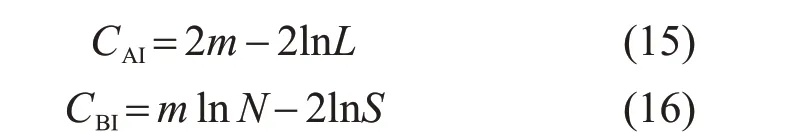
式中：m為模型獨立參數個數；S為極大似然估計值；N為樣本容量。CAI和CBI值越小，表明模型對數據的擬合度越高，模型越準確[23-24]。

1.6 產生相關性樣本

具有相關性的風電場功率、光伏電站功率、電網負荷三者樣本的產生步驟[19]如下：

1） 采用擬蒙特卡羅方法(Quasi-Monte Carlo)[25]隨機生成N個服從獨立均勻分布的n維樣本z1,z2,…,zn。

2）令z1=u1=F(x1)為第一維的采樣點。根據式(2)可得出

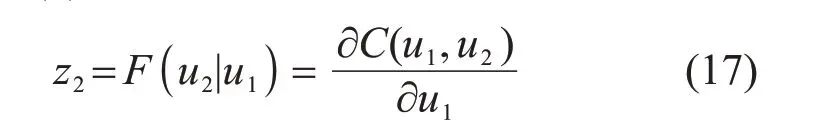
其中z2和u1已知，通過二分法求解式(17)，可得到u2。

3）同理，根據式(2)依次迭代可以得出后續的采樣點u3,u4,…,uk。

4）通過xk=F-1(uk)求逆，可得到x1,x2,…,xk。

2 考慮風光荷相關性的含儲能發輸電系統可靠性評估

由于風能、光伏以及電網負荷具有時變特性，序貫蒙特卡羅仿真方法能更好地模擬含風光儲電力系統實際運行情況。風光儲協調運行的發輸電系統可靠性指標，根據對應于所選系統停運狀態的負荷消減以及發生的概率計算得出。基于序貫蒙特卡羅仿真的含風電場、光伏電站、儲能電站的發輸電系統可靠性指標計算流程如圖2所示。

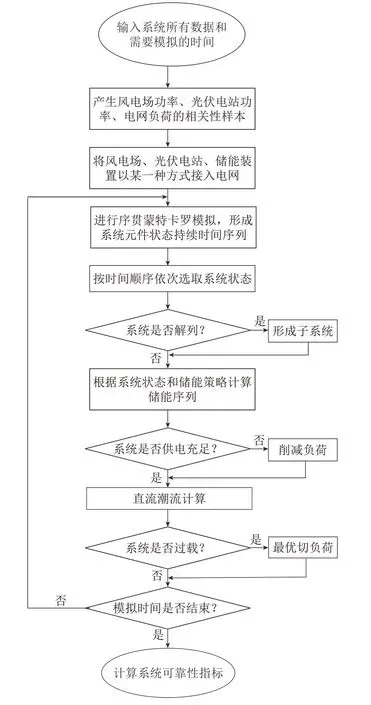
圖2 含風光儲的發輸電系統可靠性指標計算流程圖Fig.2 Flowchart of wind-solar-storage power station integrated generation and transmission systems

儲能電站與風光發電機組之間的協調控制策略選擇，需要兼顧風光儲發輸電系統可靠性水平、風光儲總輸出功率穩定、儲能電站壽命3個因素，文獻[26]提出一種平衡發電功率策略模型，在盡可能保持風光儲總輸出功率穩定的情況下，既能降低系統風險水平，又能盡量減少儲能充放電頻率，延長其壽命。

引入風光儲聯合系統輸出功率波動ξ，用來評價儲能控制功率波動效果：

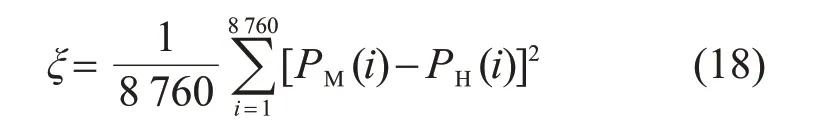
式中：PM(i)為風光儲聯合發電功率；PH(i)為風光儲系統的發電平衡限制功率。

引入儲能電站不可放電率φ，用來評價儲能容量的選擇是否合適：

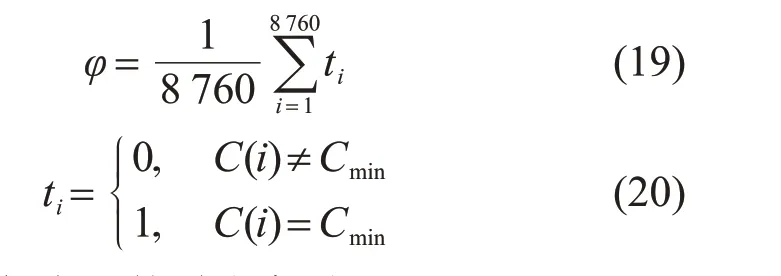
式中Cmin為儲能電站的最小容量。

3 算例分析

3.1 分析步驟

1）相關性模型的驗證。Copula 模型建立后，首先需要對其擬合的優良程度進行判別，然后才能進行理論和實際分析。檢驗Copula 模型的擬合優度，是為了評估該模型是否適用于描述變量間的相依關系。本文模型采用AIC 和BIC 對擬合優度進行檢驗。

2）計及風電場功率、光伏電站功率、電網負荷三者間相關性的發輸電系統可靠性評估計算以及結果分析。

3.2 算例系統以及數據

本文所用數據為位于山東煙臺和威海的海上風電場和光伏電站功率的年小時數據。對原IEEE-RTS79系統[27]進行適當修改，系統的2條不同電網負荷曲線不變，一條代表230 kV區域內的客戶，另一條代表138 kV區域內的客戶。200 MW風電場、20 MW光伏電站和60 MW×2 h儲能電站的聯合系統分別接入IEEE-RTS79 系統節點1、3，將修改后的系統作為算例系統。

3.3 Copula函數的選取分析

本文用8種不同類型的Copula函數來描述風電場功率、光伏電站功率和電網負荷三者間的相關結構，并分別對8類Copula函數參數進行求解，比較其AIC與BIC值，結果如表1所示。

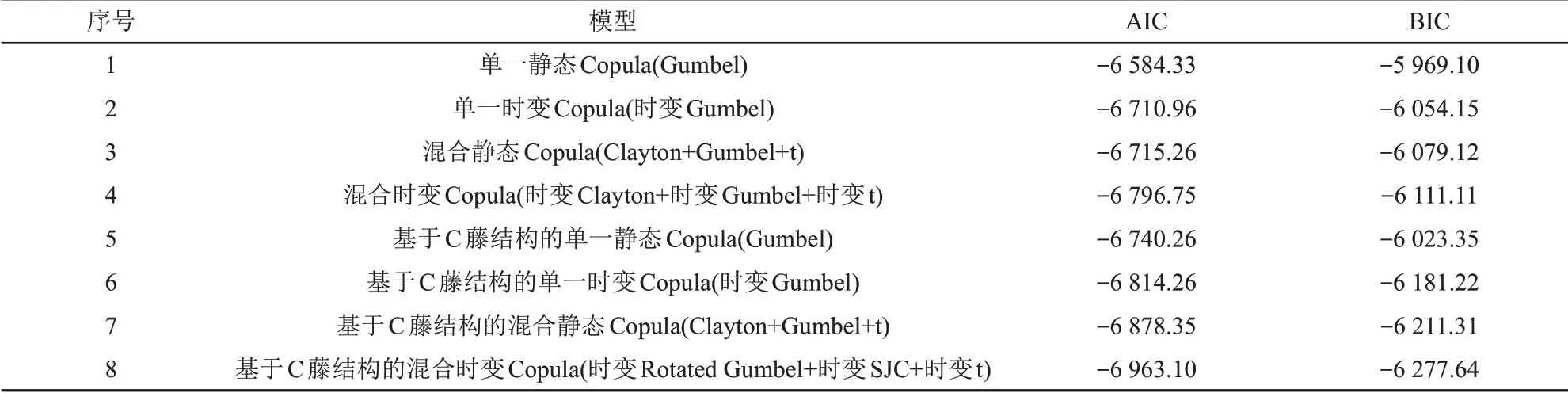
表1 不同模型擬合效果對比Tab.1 Comparison of fitting effects of different models

根據AIC 值和BIC 值判斷準則，AIC 和BIC值越小，擬合效果越好。通過比較表1 中AIC 和BIC 值可以得出：在刻畫風電場功率、光伏電站功率以及電網負荷三者間相關特性時，基于C 藤結構的混合時變Copula 函數表現最好，其次是基于C 藤結構的混合靜態Copula 函數，單一靜態Copula 函數表現最差；藤結構的Copula 函數擬合效果均好于同類型非藤結構Copula 函數，說明藤結構的Copula 函數能更有效地揭示數據間隱藏的相關結構；時變Copula 函數的擬合效果均好于同類型靜態Copula函數，說明采用時變Copula函數能更好地描述風電場功率、光伏電站功率以及電網負荷三者間相關性隨時間變化特征。

3.4 發輸電系統可靠性評估

3.4.1 系統參數說明

風光荷間相關性、風光配置比例、系統輸出功率波動性和儲能電站的容量是含風光儲發輸電系統可靠性規劃不可忽視的因素。采用8 類Copula 函數模型來描述風電場功率、光伏電站功率以及電網負荷三者間相關性結構，模擬產生風電場功率、光伏電站功率以及電網負荷的相關性樣本，依據圖2 流程對該算例系統進行了可靠性評估。為了在加入4 個新能源發電場后保持其傳輸網絡約束的有效性，系統的總負荷增加到原來的1.06 倍。傳統發電機的容量、可靠性參數、基本的負荷數據參考文獻[27]，所有發電機組的隨機失效用兩狀態模型來表示，模擬時間為100 a。風電場中風機模塊以及柔性直流輸電(voltage sourced converter based high voltage direct current，VSC-HVDC)組合系統的故障率及平均修復時間的計算方法參考文獻[7]。光伏電站中光伏逆變器和光伏陣列的故障率分別為0.353、0.000133 次/a，平均修復時間分別為240、250 h/次[28]。蓄能電站蓄電池組的故障率為5次/a，平均修復時間為70 h/次。切負荷概率(probability of load curtailment，PLC)和期望缺供電量(expected energy not supplied，EENS)是目前評估發輸電系統可靠性的2個代表性指標[26]。在不接入風電場、光伏電站和儲能電池時，IEEE-RTS79系統的EENS為1383.7 MW?h/a，PLC為0.00135。

3.4.2 風?光?荷相關性(不計儲能)

為研究風光荷相關性對發輸電系統可靠性評估的影響，算例系統暫不考慮加入儲能電站，則加入2 個風電場和2 個光伏電站的IEEE-RTS79 系統可靠性指標計算結果如表2所示。

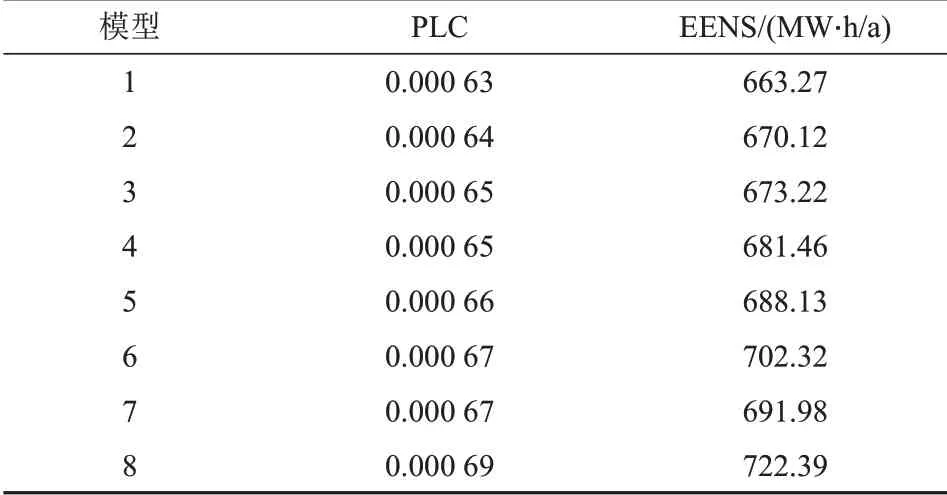
表2 加入風電、光伏電站的IEEE-RTS79系統可靠性指標Tab.2 Reliability index of IEEE-RTS79 system with wind and photovoltaic power stations

由表2 可以看出，風電場和光伏電站接入系統后，其可靠性水平明顯提高。與計及風電場功率、光伏電站功率以及電網負荷三者間相關性相比，不計及其相關性會造成對發輸電系統可靠性過于樂觀的估計。與所提出的藤Copula模型(模型8)相比，現有Copula 模型(模型1—7)低估了三者間相關性對系統可靠性產生的消極影響。采用模型8來描述風光荷相關性，通過以下5種情景驗證風光荷間不同相關特性對系統可靠性指標的影響，結果如表3所示。

表3 風光荷間不同相關特性對系統可靠性的影響Tab.3 Influence of different correlation characteristics among wind,solar and load on system reliability

情景1：考慮風電場功率W1、W2，光伏電站功率P1、P2，以及電網負荷L1、L2兩兩變量之間的相關性。

情景2：不考慮風電場功率(W1、W2)與光伏電站功率(P1、P2)之間的相關性。

情景3：不考慮風電場功率(W1、W2)與電網負荷(L1、L2)之間、光伏電站功率(P1、P2)與電網負荷(L1、L2)之間的相關性。

情景4：不考慮電網負荷L1、L2之間的相關性。情景5：不考慮所有變量之間的相關性。

由表3可知，對比情景1，忽略分布式電源功率間相關性(情景2)和電網負荷間相關性(情景4)，都會導致計算出的系統可靠性指標偏低。相反地，忽略分布式電源功率和電網負荷間相關性(情景3)，會導致計算出的系統可靠性指標偏高。情景5中不考慮所有變量兩兩間的相關性，結合情景2、4對系統可靠性指標的低估部分和情景3對可靠性指標的高估部分相互抵消，最終導致系統可靠性指標偏低。由此可知，忽略風光荷間任何2 個變量間的相關性都會影響系統可靠性的真實評估。

3.4.3 風光配置比例(不計儲能)

風光裝機容量比例也是影響系統可靠性的一個重要因素，風光裝機容量比例不同，系統的可靠性評估指標往往也不同。當系統中風光裝機容量比例達到最優時，該系統的可靠性指標EENS和PLC 值最小。同樣采用8 類模型來描述風光荷間相關性，暫不考慮系統加入儲能電站。假設一組200 MW 風電場、20 MW 光伏電站接入IEEERTS79系統節點3保持不變，另一組保持風電場、光伏電站總容量220 MW 不變，接入系統節點1，以EENS和PLC值最小為目標值，定量計算出8類模型的最優風光裝機容量比例，如表4所示。

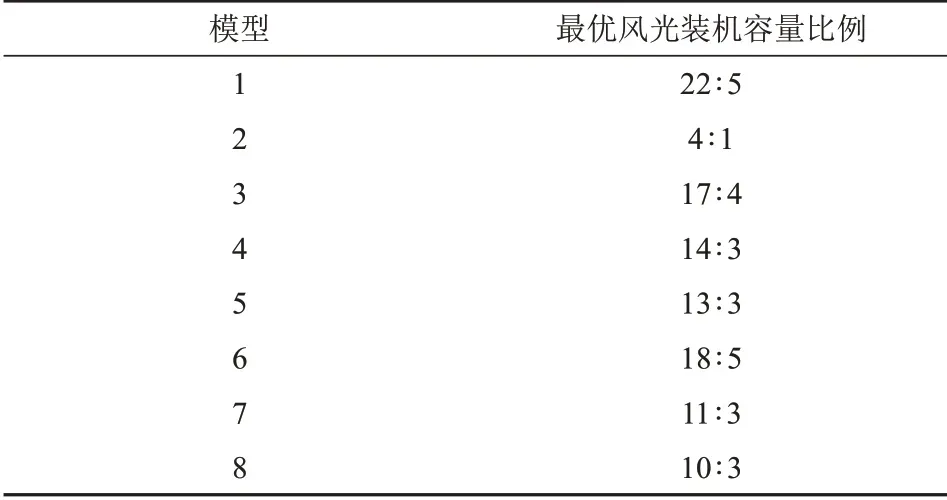
表4 最優風光裝機容量比例Tab.4 Optimal wind-solar installed capacity ratio

從表4 可以看出，采用不同的模型來表達風光荷間相關性，得出的最優風光裝機容量比例也有所不同。與所提出的藤Copula 模型(模型8)相比，采用模型1—7計算出的風光裝機最優容量比例均有所偏差，說明如果采用模型1—7去描述風光荷相關性，得出的最優風光裝機容量比例往往是不夠準確的，甚至是錯誤的。

3.4.4 風光儲協調運行

算例系統計及儲能電站，以研究儲能對系統可靠性的影響。由文獻[26]可知，當平衡發電限制功率定值接近風光發電平均功率的期望值時，風光儲有功功率波動較小。根據模型1—8，計算出此時系統可靠性指標PLC 和EENS，風光儲聯合系統輸出功率波動ξ，以及儲能電站不可放電率φ，結果如表5所示。

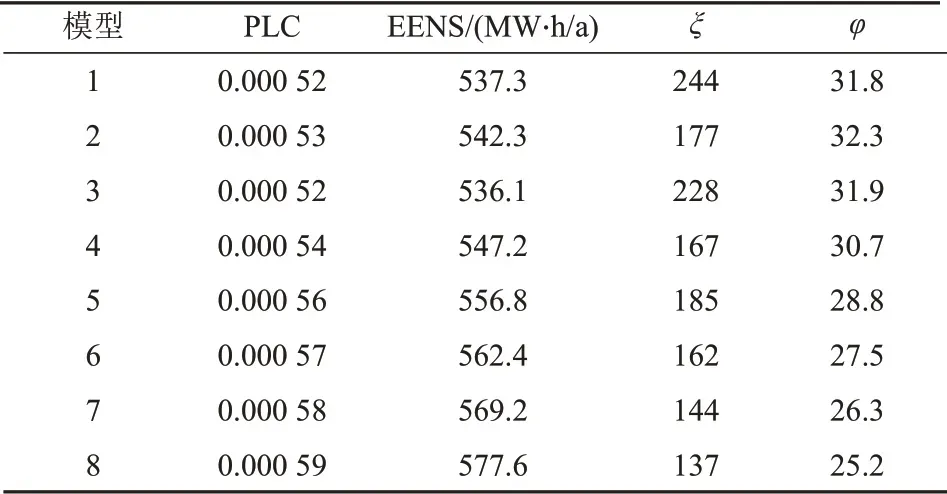
表5 風光儲聯合系統的風險評估結果Tab.5 Risk assessment results of wind-solar-storage system

通過對比表2、5可以看出，儲能容量的增加對系統可靠性有積極的影響。從表5 可以看出，采用8 類模型計算出的系統可靠性指標、儲能電站的容量、風光儲聯合系統輸出功率波動性三者均有所差異；與本文提出的Copula 模型相比，現有Copula 模型在系統可靠性評估、儲能電站容量的選取、輸出功率波動性的評價等方面均不夠準確。

4 結論

提出了一種基于藤結構的混合時變Copula 模型，并運用2 個常用最優模型評價準則對該模型進行了驗證。結果顯示，與其他現有Copula 模型相比，所提模型可以準確地描述風光荷間相關特性。從不計儲能情況下的風光荷間相關性、風光配置比例，以及計及儲能的風光儲協調運行3 個維度對所提模型和現有模型進行了對比分析，得出如下結論：

1）風光荷相關性模型的準確性直接影響系統的可靠性評估、風光裝機容量比例配置、儲能電站容量的選取和輸出功率波動性的評價。

2）引入“藤”的概念來靈活地刻畫多變量間相關關系，把高維變量間復雜相關結構逐步轉化為二維變量間的簡單相關函數，大大縮短了計算時間，對多個新能源接入的電力系統可靠性評估具有顯著的實際工程意義。

3）與所提Copula 模型相比，現有其他Copula 模型會低估風光荷間相關性對系統可靠性產生的消極影響，得出的最優風光裝機容量比例、系統輸出功率波動性評估和儲能電站容量選取方面也有所偏差。

需要注意的是，采用藤結構的混合時變Copula 模型的參數較多，隨著維數的增加，模型參數以及計算時間均將大幅增加，下一步將考慮對藤結構進行簡化，以減少模型參數、縮短運算時間。