跳車作用下新型波形鋼腹板組合梁橋的動力響應分析

于海峰，胡世浩

（1.蘭州交通大學 土木工程學院，蘭州 730070；2.上海市城市建設設計研究總院（集團）有限公司，上海 200125）

基于傳統的鋼-混組合梁橋，Nie等［1］提出了將帶肋鋼底板代替傳統混凝土底板的新型波形鋼腹板組合結構，由此出現了一種新型波形鋼腹板組合梁橋，如圖1所示.這種新型組合橋梁可以有效減輕橋梁自重，充分發揮材料潛能，提高預應力施加效率.近年來，在國內外橋梁建設與應用研究中得到了廣泛關注［2-4］.

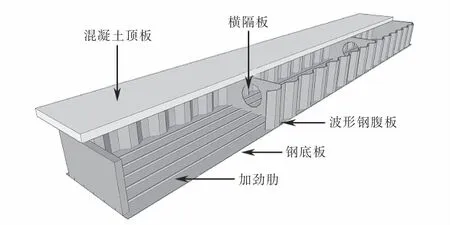
圖1 新型波形鋼腹板組合梁橋示意圖Fig.1 Diagram of the new-type box girder bridges with corrugated steel webs

現實中車輛行駛通過橋梁時，橋面可能存在障礙物，車輛通過障礙物會產生跳躍沖擊現象.車輛跳車不僅會引起橋梁結構和車輛的損害，嚴重的還可能會影響車輛的行駛安全，從而導致交通事故［5-6］.隨著現代交通事業的飛速發展，近年來公路橋梁車輛跳車問題受到了眾多學者的關注.大多數學者針對車輛跳車的研究主要集中于原因探究和防治措施等定性分析方面［7-8］，也有學者通過試驗手段或解析方法研究車輛跳車問題.潘曉東等［9］通過大量的調查統計和行車試驗研究了車輛跳車對駕駛舒適性的影響；張麗芳等［10］建立了5參數的車輛模型，分析了橋面沉降、車輛行駛速度等參數對簡支梁橋動力響應特性的影響，但該5參數車輛模型與實際情況下的車輛結構相差較遠；劉習軍等［11］通過連續的小波分析方法，研究了各種道路工況下發生車輛跳車時對橋梁結構的沖擊效應，較為準確地得到了橋梁不同部位發生車輛跳車時的動力響應.但是由于試驗手段進行成本較高，因此有必要通過數值模擬的方法，采用更加合理的車輛模型和橋梁模型來深入研究跳車作用下的車橋耦合振動響應.

為科學定量地研究車輛跳車作用下新型波形鋼腹板組合梁橋的動力響應特性，以一座跨徑為30 m的新型波形鋼腹板組合梁橋為研究對象，通過Universal Mechanism（UM）和ANSYS軟件進行聯合數值仿真研究了不考慮車輛跳車和考慮車輛跳車兩種工況下橋梁的動力響應，計算了多因素影響下橋梁在移動車輛荷載作用下的動力沖擊系數，并將結果與規范［12］中定義的動力沖擊系數設計值進行了比較.

1 車橋耦合振動仿真模型

1.1 車輛模型的建立

選用與實際情況更相符的車輛模型對于準確獲取梁橋動力響應至關重要.本文采用了更加符合實際情況的三軸車輛模型，該車輛模型的合理性在相關研究中已得到驗證［13-14］.該車輛的相關參數取值如表1所列.如圖2所示，MC，JC和IC分別代表車體質量、俯仰慣量和側傾慣量；Csi（i=1，2，…，6）和Ksi（i=1，2，…，6）表示車輛懸架阻尼和車輛懸架剛度；Mti（i=1，2，…，10）為輪胎質量；αC和βC分別為俯仰角位移和側傾角位移；Zti（i=1，2，…，10）為輪胎位移；L1，L2和L3分別表示車體質心至前、中和后軸的距離；ZC表示車體的浮沉位移；b1表示懸架中心至車輛質心軸的距離；b2表示較近一側輪胎至車輛質心軸的距離；b3表示較遠一側輪胎至車輛質心軸的距離.車輛模型通過質量、彈簧和阻尼器模擬車輛的車體、懸掛和輪胎.輪胎采用基于彈性地基梁理論的Fiala輪胎模型，車輪與橋面采用車輪圓盤模型，比單點接觸模型精度更高，能夠準確反應車輛在實際行駛過程中的動態特性，如圖3所示.

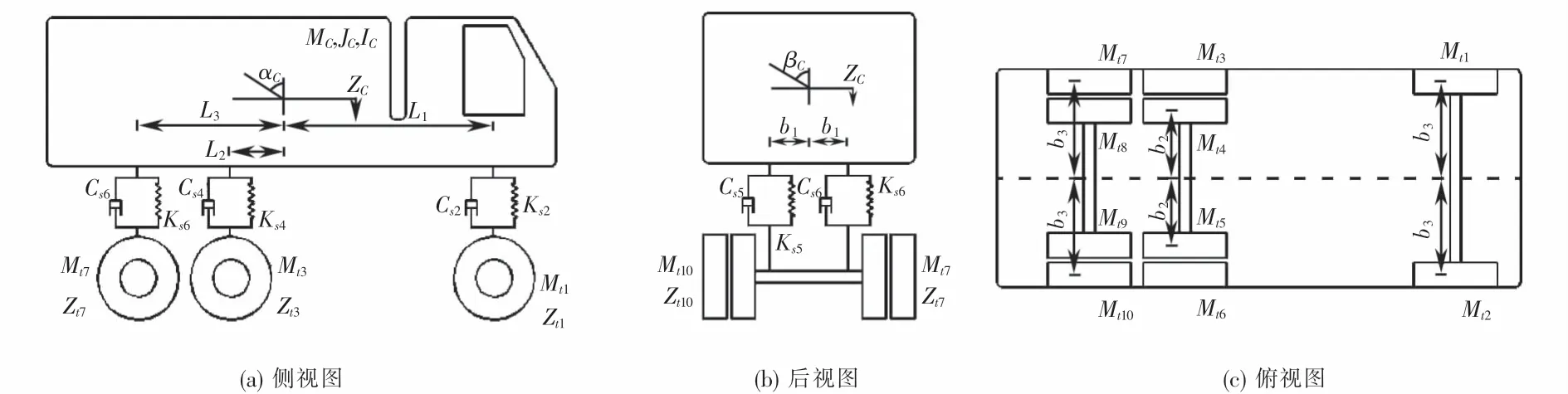
圖2 車輛模型示意圖Fig.2 Vehicle model diagram

圖3 車輛三維仿真模型Fig.3 Simulation model of the vehicle

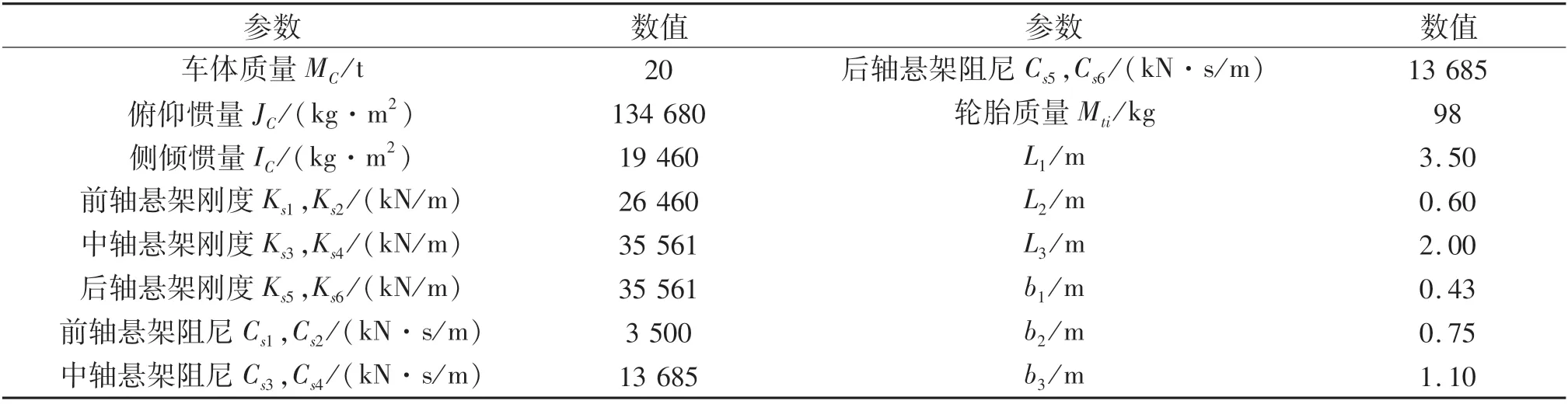
表1 車輛模型參數取值Tab.1 Vehicle model parameter value

可由達朗貝爾原理導出車輛的運動方程，表示為

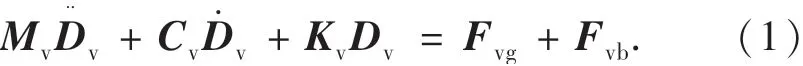
其中：Mv為車輛的質量矩陣；Cv為車輛的阻尼矩陣；Kv為車輛的剛度矩陣；Dv為車輛的位移矢量；Fvg為由車輛自重引起的荷載矢量；Fvb為輪胎變形引起的車橋相互作用力矢量.

1.2 路面不平整度模擬

1.3 跳車障礙物幾何模型

車輛跳車現象通常由橋面障礙物引起，根據規范［16］中的障礙物信息，構建了跳車障礙物的幾何模型.如圖5所示，h為橋面跳車段高度，l為橋面跳車段長度.路面不平整度提供正常段的位移激勵，橋面障礙物提供跳車段的位移激勵［17］.在整個跳車過程中，假設障礙物為剛體，同時障礙物不發生任何平動、轉動以及壓縮變形.模擬過程中將障礙物布置在橋梁跨中部位，跳車段最高點距離橋面約為5～7 cm，跳車段水平長度為30 cm，跳車時車速一般為5～20 km/h.

圖4 路面不平整度樣本曲線Fig.4 Spline curves of road roughness

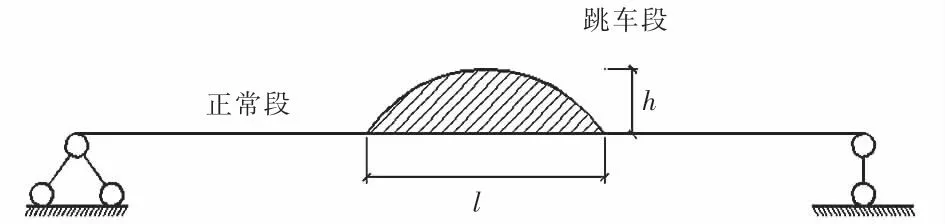
圖5 車輛跳車示意圖Fig.5 Diagram of vehicle jumping

1.4 橋梁模型的建立

甘肅省蘭州新區南立交機場連接線公路工程項目是新型波形鋼腹板組合梁橋在我國的第一次實際應用.本文的研究對象為其中一座寬20 m（4片主梁）的簡支梁橋，橋梁長為30 m，高為1.5 m，其橫截面尺寸如圖6所示.波形鋼腹板采用的是BCSW1200型號，具體尺寸如圖7所示.結構材料方面，混凝土材料為C50，鋼材采用Q345C.混凝土和鋼材彈性模量分別是3.45×104Mpa和2.06×105Mpa；泊松比分別取0.2和0.3.

圖6 橋梁橫截面圖（單位：mm）Fig.6 Bridge cross-section diagram（unit：mm）

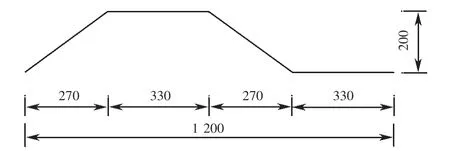
圖7 波形鋼腹板尺寸圖（單位：mm）Fig.7 Geometry of corrugated steel web（unit：mm）

通過ANSYS軟件構建橋梁的有限元模型如圖8（a）所示.其中，混凝土和鋼材分別采用SOLID45單元和SHELL63單元進行模擬.兩種單元連接節點處通過節點耦合約束的方式建立剛性區域.全橋共建立節點52 575個，單元42 514個.通過ANSYS計算得到橋梁的第一階豎向彎曲自振頻率為3.791 Hz，一階振型如圖8（b）所示.

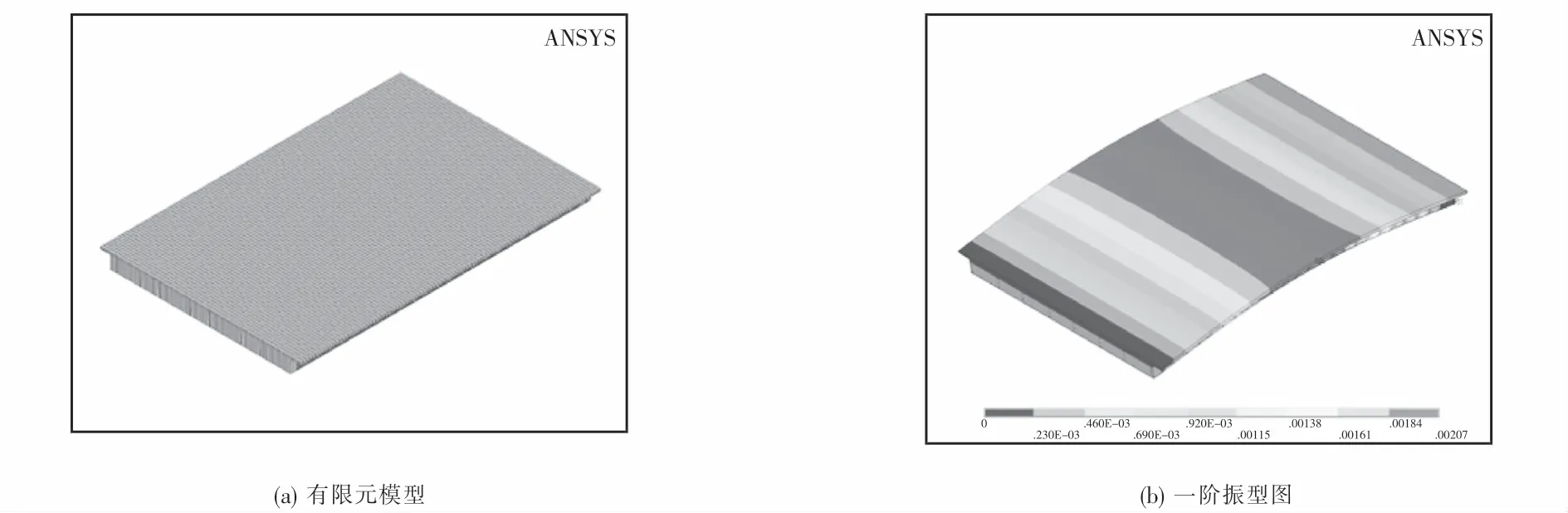
圖8 有限元模型及振型圖Fig.8 FE model and first-order mode shape of the composite girder

通過脈動法動力特性試驗獲取橋梁實測自振特性，得到前三階豎向彎曲自振頻率.橋梁現場試驗狀況如圖9所示，功率譜密度如圖10所示.

圖9 現場數據采集圖Fig.9 Data acquisition system

圖10 功率譜密度圖Fig.10 Power spectral density

通過對比橋梁自振頻率實測值與ANSYS計算值，驗證所建有限元模型的準確性，結果如表2所列.對比結果，兩者一階彎曲自振頻率的誤差僅為0.76%，數據吻合良好，表明有限元模型具有較高的準確性.

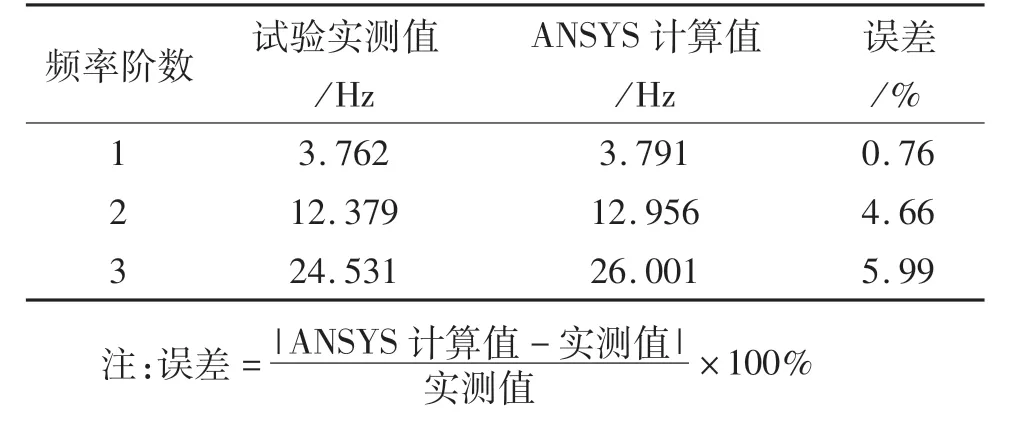
表2 豎向彎曲自振頻率實測值與ANSYS計算值對比Tab.2 Comparison of the measured value and ANSYSvalue

1.5 車橋耦合模型的建立與驗證

基于UM-ANSYS.exe接口程序將上文所建立的車輛模型和橋梁模型導入同一個UM仿真模型中，在UM軟件中設置橋梁的約束節點，將車輛模型與橋梁模型進行耦合，得到車橋耦合振動仿真模型，如圖11所示.為驗證所建車橋耦合仿真模型的適用性，在ANSYS中也采用相同車輛荷載進行多荷載步靜力加載，獲得橋梁靜撓度計算值，通過對比UM計算值，結果表明數據吻合良好，如圖12所示，最大誤差為1.48%，驗證了所建車橋耦合仿真模型的適用性.

圖11 車橋耦合模型示意圖Fig.11 Diagram of the vehicle-bridge coupled model

圖12 UM 和ANSYS靜撓度計算值Fig.12 Comparing of the static deflection of UM and ANSYS

根據車橋接觸點的位移協調關系和相互作用力關系［18］，車輛橋梁剛柔耦合模型的振動方程可表示為

上文所建立的車橋耦合動力學方程在時域和頻域內均可進行求解，采用較多的是時域計算方法中的直接積分法和綜合模態法.通過直接積分法求解可能會耗費大量資源，甚至無法求解.因此，有學者提出綜合模態法，這種新的求解方法在計算中忽略橋梁的高階模態貢獻，僅選取少量低階模態參與計算，可大幅降低求解動力學方程的復雜程度［19］.本文基于ANSYS有限元軟件建立高精度橋梁模型，采用固定界面模態綜合法求解，剔除6個剛體模態.將高精度橋梁模型和車輛模型導入UM軟件中形成車橋耦合系統，UM軟件通過Park積分法求解車橋耦合振動方程.

在UM軟件Simulation后處理程序中計算不同工況下車橋耦合振動的動力響應.具體仿真流程如圖13所示.

圖13 車橋耦合振動仿真流程Fig.13 Simulation process of vehicle-bridge coupled system

2 數值分析

車輛行駛車道選取為2號主梁所對應車道，對于簡支梁橋，橋梁的最大撓度響應和最大應變響應均出現在跨中截面.因此，選取橋梁跨中截面靜響應最大的主梁底部作為具體控制點.計算工況如表3所列.

表3 車橋耦合仿真工況設置Tab.3 Working condition of vehicle-bridge coupled simulation

2.1 未發生跳車時橋梁動力響應

2.1.1 橋梁跨中撓度

為了研究路面不平整度對橋梁跨中撓度的影響規律，研究車輛以60 km/h的速度勻速通過橋梁，獲取橋梁跨中截面控制點的撓度時程曲線，如圖14所示.

從圖14可以看出：路面不平整度對新型波形鋼腹板組合梁橋跨中撓度影響較大.隨著橋面平整狀況的不斷劣化，橋梁最大撓度波動幅度越來越大，在路面不平整度等級為好的情況下，撓度時程曲線基本呈拋物線趨勢，當路面不平整度等級為差的情況時，撓度時程曲線則出現了很大的波動，拋物線已經不再顯現.在路面不平整度等級為差的情況下，橋梁最大動撓度為3.739 mm，較路面不平整度等級為好時增加了32.7%.

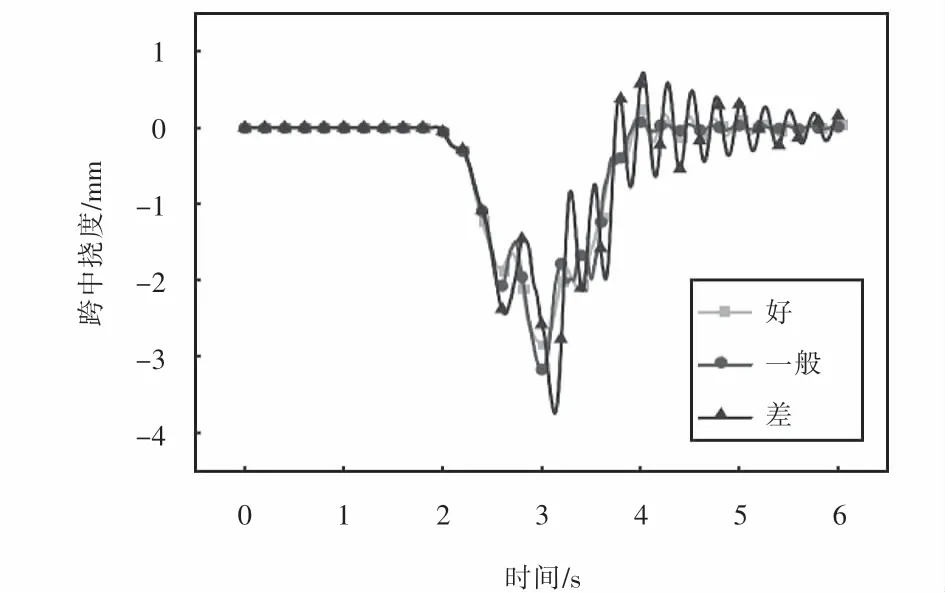
圖14 不同路面等級下的撓度時程曲線Fig.14 Deflection curves under different road roughness

2.1.2 動力沖擊系數

為了研究車輛行駛速度對動力沖擊系數的影響規律，考慮在其他條件相同時，路面不平整度等級為好、一般、差三個等級，車輛以30～120 km/h、間距為15 km/h的速度勻速通過橋梁，研究其引起的動力沖擊系數的變化規律，如圖15所示.

從圖15可以看出：在三種路面不平整度等級下，動力沖擊系數隨著車速的增加未表現出明顯的單調變化趨勢，而是整體出現先減小，后增大，再減小的變化趨勢.對比發現，當路面不平整度等級為好時，動力沖擊系數的計算值小于規范設計值；當路面不平整度等級為一般時，兩者數據吻合良好；當路面不平整度等級為差時，動力沖擊系數的計算值與規范設計值存在較大差異.因此，規范可能低估了路面狀況較差時移動車輛引起的動力沖擊效應.

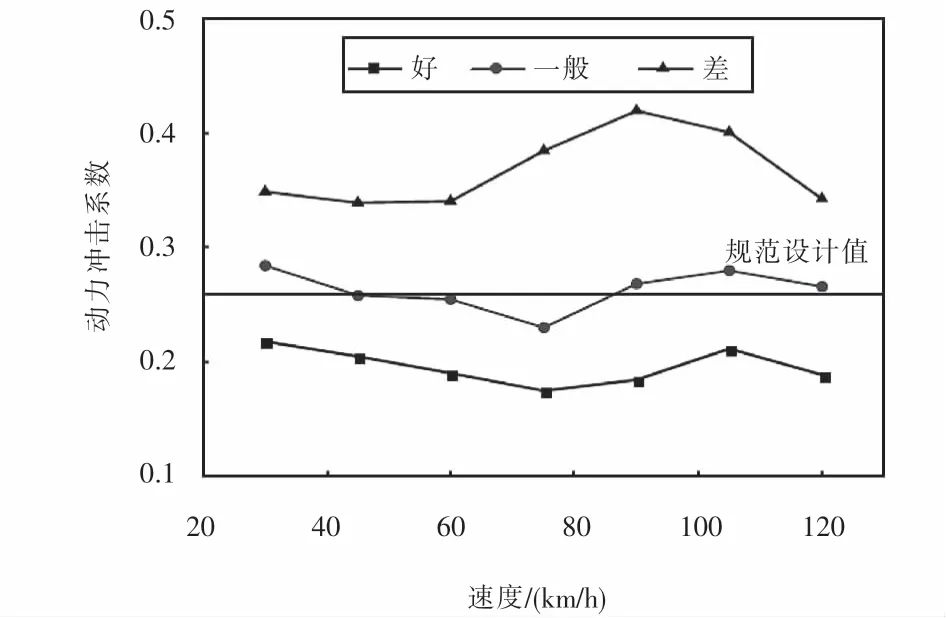
圖15 不同車速影響下的動力沖擊系數Fig.15 Impact factors under different vehicle speed conditions

2.2 發生跳車時橋梁動力響應

2.2.1 橋梁跨中撓度

車輛跳車可能會引起橋梁更明顯的動力響應［20-21］.為了研究不同跳車速度、不同跳車高度對組合梁橋跨中撓度的影響規律，考慮路面不平整度等級為好，車輛以速度為5、10、15、20 km/h勻速通過橋面，車輛起跳高度為5、6、7 cm.以5 km/h為例，得到考慮車輛跳車作用下跨中截面控制點的撓度時程曲線，如圖16所示.

將跳車行駛速度為5、10、15、20 km/h四種工況下的跳車沖擊計算結果匯總，如表4所列.

從圖16可以看出：在同一路面等級下，車輛在通過橋梁時，車輛跳車沖擊效應對橋梁跨中撓度的影響顯著.當未發生跳車時橋梁跨中撓度為2.573 mm，跳車5 cm時橋梁跨中撓度為3.607 mm，跳車6 cm時橋梁跨中撓度為3.903 mm，跳車7 cm時橋梁跨中撓度為4.546 mm.

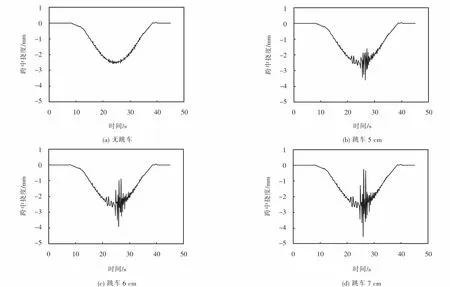
圖16 考慮橋面跳車時的撓度時程曲線Fig.16 Deflection curves considering vehicle jumping

從表4可以看出：車輛以不同行駛速度通過橋梁會引起不同的動力響應，發生跳車沖擊后，不同車速對橋梁跨中撓度影響不大.以跳車5 cm為例，車速5 km/h引起的橋梁跨中撓度最小，車速20 km/h引起的橋梁跨中撓度最大，兩者差值僅為0.331 mm.

表4 車輛以不同速度發生跳車時橋梁跨中撓度Tab.4 Bridge mid-span deflection at different vehicle jumping speeds

2.2.2 動力沖擊系數

為了研究不同跳車速度、不同跳車高度對組合梁橋動力沖擊系數的影響，假設路面不平整度等級為好，起跳高度為5～7 cm，間距為1 cm，車輛以5～20 km/h，間距為5 km/h的速度通過橋梁，研究其引起的動力沖擊系數變化規律，如圖17所示.

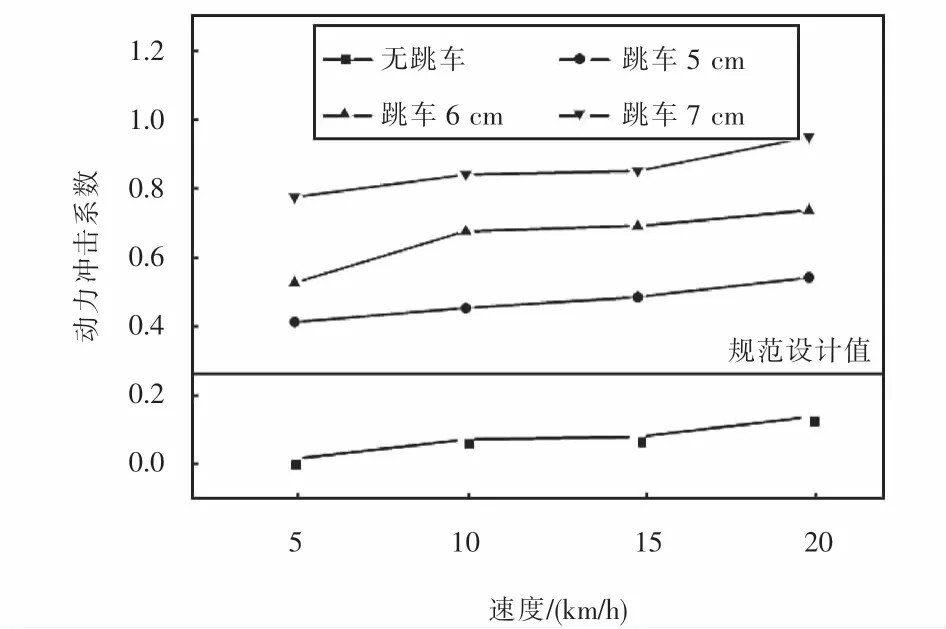
圖17 跳車影響下的動力沖擊系數Fig.17 Impact factors considering vehicle jumping

從圖17可以看出：車輛跳車對動力沖擊系數影響顯著，以20 km/h為例，當未發生跳車時最大動力沖擊系數為0.124，跳車5 cm時最大動力沖擊系數為0.531，跳車6 cm時最大沖擊系數為0.728，跳車7 cm時最大沖擊系數可達0.942.比較可知：當發生跳車沖擊時所引起的動力沖擊系數均大于規范設計值.因此，該規范可能低估了車輛跳車現象對沖擊效應的影響.當發生車輛跳車時，動力沖擊系數與車速整體呈正相關趨勢，在車速為20 km/h時動力沖擊系數達到最大值.但相較而言，跳車高度對動力沖擊系數的影響更大.

3 結論

1）聯合UM和ANSYS建立了車橋振動分析模型，對未發生車輛跳車和發生車輛跳車兩種工況下新型波形鋼腹板組合梁橋的動力響應進行了分析，為該類橋型動力沖擊系數的合理選取提供了參考依據.

2）當未發生車輛跳車時，路面不平整度對橋梁跨中撓度響應影響較大，當路面不平整度等級為差時，最大撓度較路面不平整度等級為好時增加了32.7%.同時，沖擊系數隨車速的增加沒有明顯的線性關系，而是整體呈先減小后增加再減小的變化趨勢.

3）當發生車輛跳車時，車輛跳車高度對橋梁動力響應影響顯著，不同跳車高度影響下動力沖擊系數可增加數倍.此外，車輛跳車速度與橋梁動力響應整體呈正相關趨勢，但其對橋梁動力響應影響不大.

4）現行起橋梁設計規范可能低估了較差路面狀況和車輛跳車現象對動力沖擊效應的影響.