Quantum fields presentation and generating functions of symplectic Schur functions and symplectic universal characters

Denghui Li(李登慧), Fei Wang(王菲), and Zhaowen Yan(顏昭雯)

School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China

Keywords: quantum fields, generating functions, integrable systems, symmetric functions, boson–fermion correspondence

1. Introduction

Symmetric functions play a significant role in mathematical physics[1]especially in integrable systems.[2–6]The most elementary symmetric functions are Schur functions which are the solutions of differential equations in Kadomtsev–Petviashvili(KP)hierarchy.[7,8]Symplectic Schur function is the character of the irreducible highest weight representation of the symplectic group.Baker[9]presented the quantum fields presentation of the symmetric functions and studied the properties and applications of the vertex operators. Later,the generalization of symplectic Schur functions as well as the corresponding integrable systems have been well investigated.[10,11]

The universal character proposed by Koike[12]is the extension of the Schur function. Tsuda[13]developed a novel integrable system called universal character (UC) hierarchy with the property of the universal character, which is a generalization of the KP hierarchy. Then,Painlev′e equations and their higher order analogues have been derived from KP hierarchy and UC hierarchy via reduced Virasoro constraints.[14]Later on, the universal characters with various systems includingq-Painlev′e systems,q-difference Painlev′e equations,phase model and topological strings are well discussed.[15–19]Recently, Wanget al.[10]established a symplectic universal character(SUC)hierarchy which can be regarded as the generalization of SKP hierarchy and indicated the SUC hierarchy characterized by symplectic universal characters.

Vertex operators discovered in string theory are important research objects in mathematics.[20–22]Several symmetric functions can be realized by acting certain vertex operators on the constant function 1.[23–27]It has been shown that symmetric functions are closely connected to boson–fermion correspondence.[28]In Ref. [26], based upon the quantum fields of operators,the twisted quantum fields presentation of Hall–Littlewood polynomials has been derived and the authors extended a new deformed boson–fermion correspondence. Inspired by the connection between quantum fields and generating functions of the symmetric functions,in this paper,connecting with the charged free fermions,we will concentrate on the construction of quantum fields of symplectic Schur functions,universal characters and symplectic universal characters.Furthermore, the generating functions of the corresponding symmetric functions are obtained by the action of the vertex operators on the constant function 1. By means of the quantum fields of operators,we obtain a novel boson–fermion correspondence of these symmetric functions and a series of infinite order nonlinear integrable equations. Meanwhile,the solutions of these nonlinear integrable equations have been studied.

The present paper is built up as follows. In Section 2,we begin with a review of the elementary basics of symmetric functions involving Schur functions. Section 3 is devoted to construction of quantum fields and generating functions of universal characters. In Section 4, we derive the quantum fields presentation and generating functions of symplectic Schur function and symplectic universal character. Meanwhile, we present the corresponding integrable systems of these symmetric functions and develop their solutions. The last section is a summary and discussion.

2. An introductory discussion of symmetric functions

We retrospect some basic facts about symmetric functions including Schur functionsSλ(x)and the action of operators on the ring of symmetric functions.

2.1. Symmetric functions

The ringΛ(x)is made up of symmetric functions in variablesx=(x1,x2,...). Therth elementary symmetric functioneris the sum of all products ofrdistinct variablesxi, and it can be written as

2.2. Schur functions and KP hierarchy

Proposition 5 All the Schur functionsSλ(x)are the solutions of the KP hierarchy.

3. Universal characters and UC hierarchy

In this section, let us construct quantum fields and generating functions of the universal charactersS[λ,μ](x,y) and define an integrable system called UC hierarchy which are different from that in Ref.[13].

For each pair of partitions

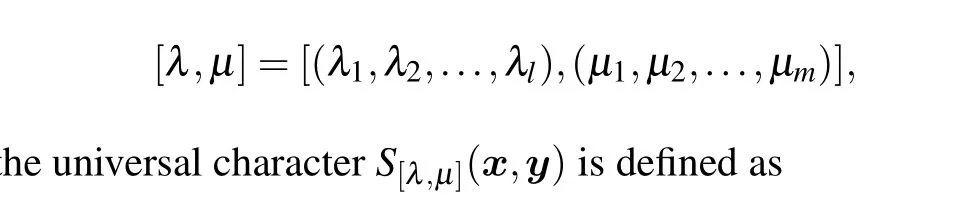
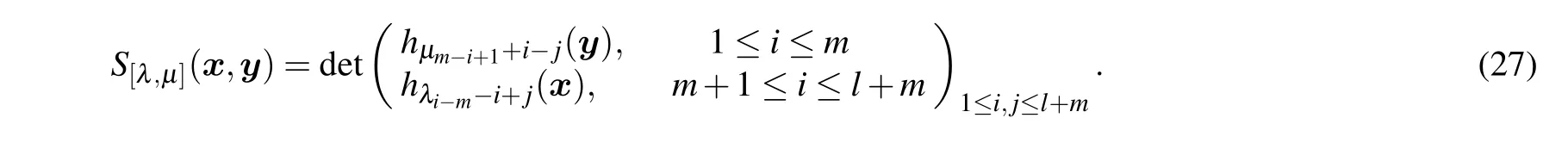
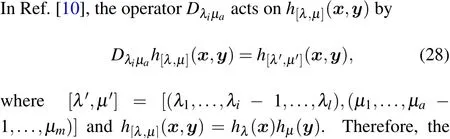
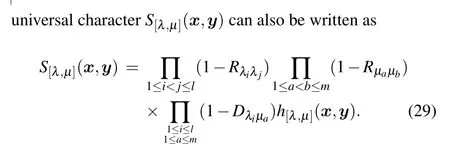
Multiply the first formula byvand the second formula byu,and then subtract to obtainvΦ+(u)Ψ+(v)?uΨ+(v)Φ+(u)=0. The proof method of the rest of the proposition is similar and will not be given here.

Proposition 6 immediately indicates that the formal distributionsΦ±(u) andΨ±(u) provide the quantum fields presentation of universal characters. Letvm

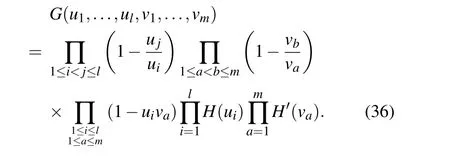
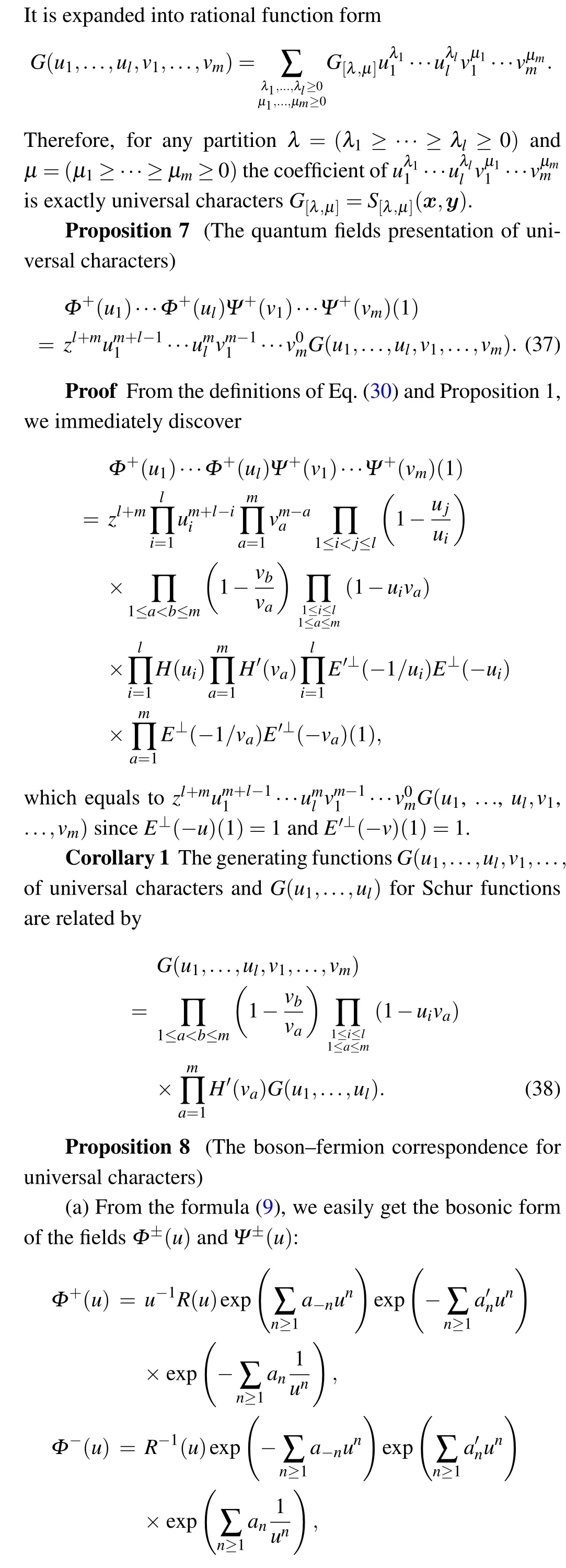
4. Symplectic Schur functions and generalized symplectic Schur functions

4.1. Symplectic Schur functions and SKP hierarchy

4.2. Symplectic universal characters and SUC hierarchy

In this part,we transfer our research goal to the symplectic universal characters. We will give the quantum fields presentation and the boson–fermion correspondence for the symplectic universal characters. Then, we will construct a modified type of the system of bilinear equations and discuss the solutions of this system.

For each pair of partitions

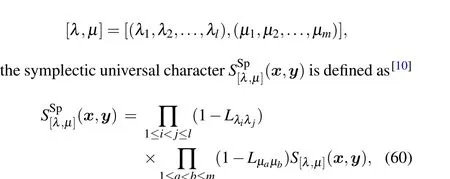
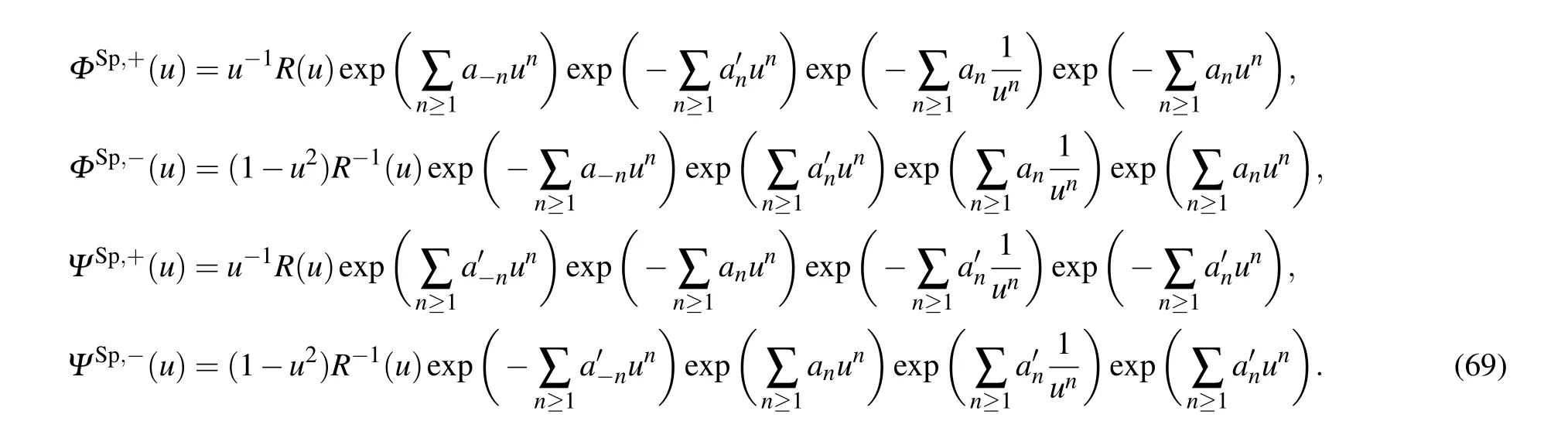
5. Summary and discussion

In this paper,we have discussed quantum fields presentation and generating functions of the universal characters,symplectic Schur functions and symplectic universal characters. It should be pointed out that the generating functions play a key role in constructing the vertex operators of symmetric functions. Furthermore,based upon the boson–fermion correspondence for the symmetric functions, we have derived infinite order nonlinear partial differential equations, namely UC hierarchy,SKP hierarchy and SUC hierarchy. Moreover,corresponding solutions of these equations have also been derived.It is worthwhile to mention that finding the exact solutions of these partial differential equations is difficult. Therefore, the relation of quantum fields operators may shed light on the solutions of these equations, which will be studied in the near future.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11965014 and 12061051) and the National Science Foundation of Qinghai Province, China(Grant No.2021-ZJ-708).The authors gratefully acknowledge the support of Professor Ke Wu and Professor Weizhong Zhao at Capital Normal University,China.