基于級聯四波混頻過程產生四模簇態*

董安琪 張凱? 荊杰泰2)3)? 劉伍明

1)(華東師范大學,精密光譜科學與技術國家重點實驗室,上海 200062)

2)(中國科學院超強激光科學卓越創新中心,上海 201800)

3)(山西大學,極端光學協同創新中心,太原 030006)

4)(中國科學院物理研究所,北京凝聚態物理國家研究中心,北京 100190)

5)(中國科學院大學物理科學學院,北京 100190)

6)(松山湖材料實驗室,東莞 523808)

簇態是量子計算和量子信息處理的重要資源,因其具有獨特的糾纏性質和豐富的結構而受到廣泛的關注.本文從理論上提出一種基于級聯四波混頻過程產生四模糾纏態的方案,利用部分轉置正定判據和本征模分解研究其內部糾纏特性.此外,通過調控平衡零拍探測的相對相位和后處理噪聲信號,將輸出的糾纏態重構優化,最終生成三種不同結構的四模簇態.該方法可以有效地減少在有限的壓縮條件下產生簇態而引入的額外噪聲.本文理論結果為基于原子系綜四波混頻過程產生可擴展的連續變量簇態提供可靠方案.

1 引言

連續變量簇態作為一種重要的物理資源,在基于測量的量子計算和量子信息處理領域起著至關重要的作用[1].為了在真實物理系統中實現可擴展的量子計算,研究者們已經在理論上提出多種方案,并且在不同系統中進行了實驗,其中單向量子計算機是基于測量的量子計算的重要理論框架[2],因此,簇態作為單向量子計算的基本資源而得到廣泛的關注.依據特定的順序和測量基矢對簇態做單模測量就可以實現量子計算[3].在連續變量系統中,通常使用線性分束器網絡耦合多個獨立的單模壓縮態來構造連續變量簇態[4,5].然而,隨著糾纏模式數的增加系統的復雜性也急劇增加.目前最新研究趨勢是通過空間[6]、時間[7-9]和頻率[10,11]復用多個非線性過程形成量子網絡,這些方法產生的簇態適用于量子計算,但是由于產生的光束不易空間分離,所以很難應用在量子通信網絡.因此,需要一種可擴展的確定性產生的方法生成空間分離的簇態.

基于熱銣原子系綜的四波混頻(four-wave mixing,FWM)過程由于其獨特的優勢,已經證明是量子信息處理的重要資源[12-16].該系統由于原子相干特性而具有很強的非線性效應,使系統不需要借助光學腔而具有空間多模性,因此產生空間分離的非經典光束[17].利用四波混頻的空間多模特性[18-19],可以將相互正交的軌道角動量模式引入產生多組并行的連續變量糾纏[20-22],利用軌道角動量模式匹配的參量放大器實現多通道量子隱形傳態[23].四波混頻因空間多模特性而成為高容量連續變量量子信息處理的重要資源.這些特點使得基于原子系綜的四波混頻過程取得一系列重要的研究進展,例如實現全光量子隱形傳態[23]、可控的量子態延遲[24]、量子密集編碼[25]以及量子克隆等[26].基于該系統的獨特優勢,本文理論上提出一種基于級聯四波混頻過程產生四模糾纏態的方案,通過非對稱結構級聯三個熱銣原子池確定性地產生空間分離的四模糾纏態.然后,通過優化算法后處理從一組初始的正交振幅和正交相位壓縮態重構出多模簇態,這種方法可以減小在有限壓縮的條件下產生簇態而引入的額外噪聲[27-29].該方法通過調控平衡零拍探測的本振光和信號光的相對相位和利用實數正交矩陣來重組優化結果以生成不同結構的簇態.

2 基于級聯四波混頻過程產生四模糾纏態

2.1 理論模型

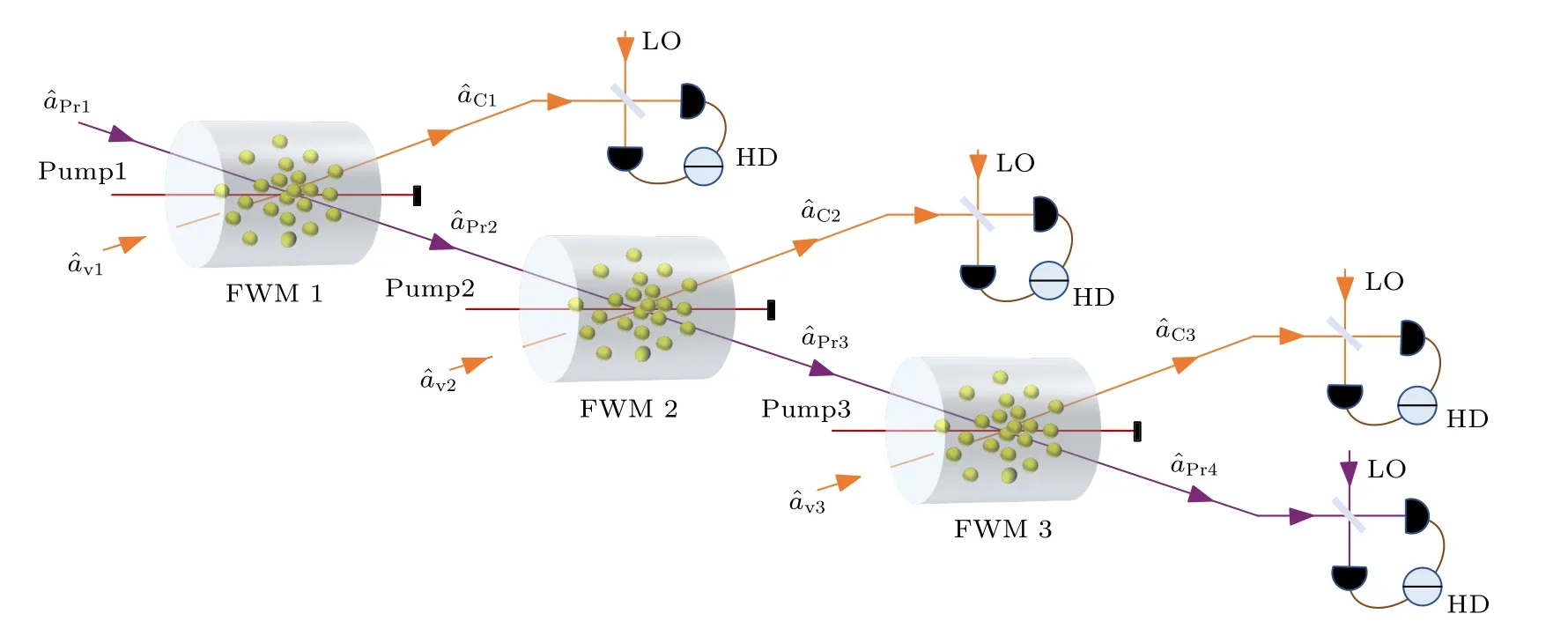
圖1 通過非對稱結構級聯三個四波混頻過程產生四模糾纏態的示意圖.,和是四波混頻過程FWM1,FWM2和FWM3 的信號光;,和是真空輸入模式;,,和是最終輸出的四個模式;Pump1,Pump2和Pump3 表示三個四波混頻過程的泵浦光;LO 表示用于平衡零拍探測(HD)的本振光場Fig.1.Schematic diagram of four-mode entangled states generated by cascading three four-wave mixing processes with asymmetric structure., and are seed beams of FWM1,FWM2 and FWM3,respectively., and are vacuum input modes.,, and are the final four output modes.Pump1,pump2 and pump3 denote the pump light of three fourwave mixing processes.LO denotes the local oscillator for balanced homodyne detection (HD).

2.2 四模量子糾纏特性

為了檢驗基于級聯四波混頻過程產生的四模態糾纏情況,利用部分轉置正定判據來判斷該體系產生的四模態是否糾纏[31,32].部分轉置是反轉正交相位算符的符號,即轉置為,k是被轉置的光束.因此,部分轉置的協方差矩陣可以表示為:σ′T2NσT2N,其中T2N表示 2N維的對角矩陣,并且除了T2k,2k-1 以外的所有對角元素均為1.通過轉置部分協方差矩陣把體系分成兩部分,從而判斷這兩部分的糾纏情況.對于N模系統,需要驗證 2N-1-1 種可能的兩分情況,如果所有的兩分情況均不可分,就可以證明產生了真正的N模糾纏態.這里協方差矩陣的表達式定義為σ〈ζζT〉,可以將四個模式的正交分量的對易關系寫為,其中1和-1 分別表示對角元素為1和—1 的對角矩陣.對于高斯態的協方差矩陣必須滿足不確定性關系:σ+iΩ≥0,這意味著σ≥0,即協方差矩陣的所有最小辛本征值應大于等于1.部分轉置后的協方差矩陣最小辛本征值可以通過求解 iΩσ的本征值得到,當最小辛本征值小于1 時證明存在糾纏.對于四模態系統有兩種兩分情況需要分析,即4 種1×3和3 種2×2,共7 種情況.圖3 展示了不同強度增益下7 個最小辛本征值的計算結果,結果表明7 種情況的最小辛本征值均小于1,并且隨著強度增益的增加最小辛本征值逐漸減小,說明產生真正的四模糾纏態.

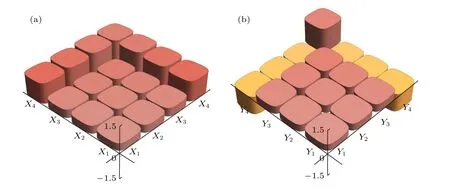
圖2 當 G1=G2=G3=1.2 時四模態系統的協方差矩陣 (a)正交振幅的協方差矩陣 〈〉;(b)正交相位的協方差矩陣〈〉Fig.2.The covariance matrix of the four-mode state int he caseof G1=G2=G3=1.2 : (a)The covariance of amplitude quad-ratures 〈〉;(b)the covariance of phase quadratures 〈〉.

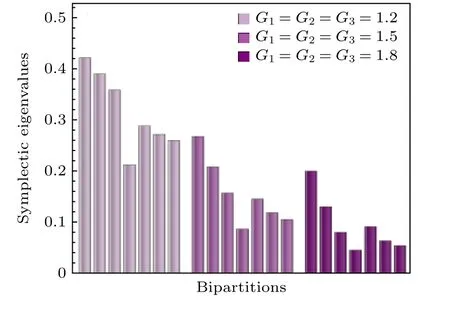
圖3 不同強度增益情況下,四模態的最小辛本征值.不同顏色的條形圖分別表示強度增益為1.2,1.5和1.8 時的最小辛本征值Fig.3.The smallest symplectic eigenvalues of four-mode state for different gains.Bar chart with different colors represent the smallest symplectic eigenvalues at gains of 1.2,1.5 and 1.8,respectively.

2.3 本征模

為進一步研究四模態系統內部的糾纏結構,還分析了系統中的本征模.多模高斯態經過Bloch Messiah 分解可以得到一組相互正交的單模壓縮態和線性分束器網絡[33].分解過程可表示為σXX其中Kdiag(η1,η2,···)是由本征分解協方差矩陣得到的特征值組成的對角矩陣,其值在對數空間代表單模壓縮態的壓縮度,U0是本征分解協方差矩陣得到的本征向量,其可以用線性分束器網絡實現.這里我們分解協方差矩陣中與正交振幅相關的部分(分解協方差矩陣的正交相位部分和正交振幅部分結果相似),選擇強度增益G為1.2,1.5和8,分別得到本征值和對應的本征向量如圖4 所示.通過對本征模進行分析,發現經過級聯四波混頻過程產生的四模糾纏態可以等價為兩個單模壓縮態和兩個真空態經過線性分束器網絡得到.同時發現壓縮值隨著強度增益G的增加而變大,這意味著糾纏度增強.值得注意的是隨著強度增益G的增加,壓縮模和反壓縮模中的和在四個模中占的相對權重變低,使得相應模式對整體的糾纏影響逐漸變小,這是由于系統的非對稱結構導致的.

圖4 對于不同強度增益 G,基于級聯四波混頻過程生成的四模糾纏態的本征模及其相應的壓縮值.每幅圖中的條形柱分別表示模,,和 的相對權重,圖上面的數字代表壓縮值.圖(a)—(d),圖(e)—(h)和圖(i)—(l)分別對應強度增益 G 為1.2,1.5和8 時的本征模分解情況Fig.4.The supermodes of the four-mode entangled state generated based on the cascade four-wave mixing process and their corresponding squeezing levels for different gain values G.The bars represent the relative weight of the modes,,and,respectively.The number above the figure represents the squeezing levels.Figures (a)—(d),Figures (e)—(h)and Figures (i)—(l)correspond to the eigenmode decomposition when the gain values G are 1.2,1.5 and 8,respectively.

3 基于級聯四波混頻過程產生四模簇態

多模糾纏態作為量子信息技術的重要資源,不僅是基礎量子理論領域[34],也是量子計算和量子信息處理應用領域的重要研究課題[35-41].簇態是具有很強的糾纏保持特性和豐富結構的多模糾纏態,作為量子計算的重要平臺而得到廣泛研究.第二節已經證明基于級聯四波混頻過程的輸出態是四模糾纏態,本節通過操縱這些輸出態生成連續變量簇態.

簇態的相互作用僅局限于相鄰模式之間,各結點通過糾纏連接.在理想壓縮的情況下,連續變量簇態定義為

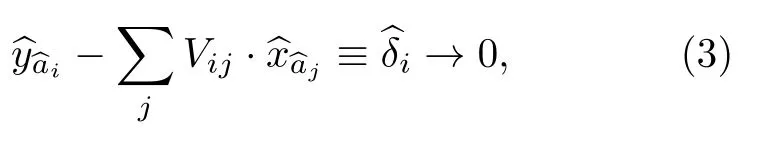
根據簇態的定義,構造簇態的光學網絡可以通過一個酉矩陣UV描述.文獻[45]中已表明矩陣UV可分解為

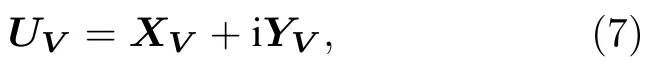
其中XVRe[UV],為矩陣UV的實數部分;YVIm[UV],為矩陣UV的虛數部分.設此簇態在理想情況下對應的鄰接矩陣為V,該簇態的正交分量滿足(3)式,所以XV,YV和V之間滿足如下關系:

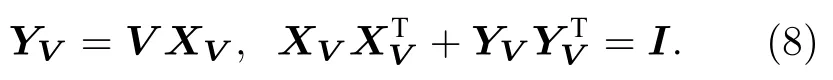
在四波混頻系統中可以從一組初始的正交相位壓縮態經過后處理變換得到簇態.首先引入對角移相矩陣D,通過對輸入態進行 π /2相移使正交振幅壓縮變為正交相位壓縮,從而使得所有輸入模式均處于正交相位壓縮態.在第二節將正交振幅的協方差矩陣進行本征模分解得到一個正交相位壓縮態、兩個真空態和一個正交振幅壓縮態,因此移相矩陣的具體形式為Ddiag(1,1,1,I).在四波混頻系統中酉矩陣UFWM可以表示為UFWMU0D,其中U0是第二節中本征分解協方差矩陣得到的本征向量[46].然后,根據文獻[29],引入兩個變換對輸出的糾纏態優化后處理得到滿足條件的簇態.總的變換結果U可表示為

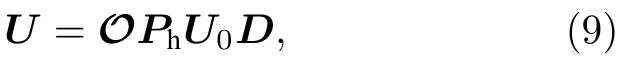
其中Phdiag(ei?1···ei?N)是對本振光和信號光之間的相對相位進行相移的對角矩陣.實驗上通過控制每個平衡零拍探測本振光和信號光的相對相位來實現.實數正交矩陣O可以通過調節噪聲信號的增益或衰減來優化重構結果.此時得到的簇態的每個結點不是空間分離的單一模式,而是多模糾纏態的疊加[10].將變換的結果與給定的簇態轉換矩陣UV作比較,可以找到一組參數滿足如下關系:

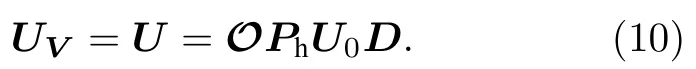
那么就實現了從四波混頻系統生成的糾纏態經過平衡零拍探測的相位調控和輸出信號的后處理到連續變量簇態網絡的轉變.這種變換存在一些特征,定義矩陣,其中是對角矩陣,并且是(10)式成立的充分必要條件.整理替換以上方程式可以得到:

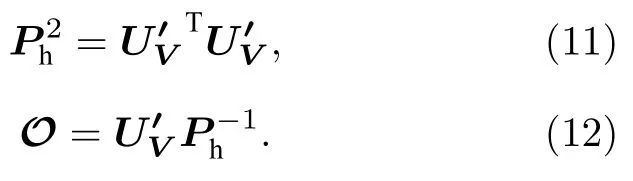
接下來將說明如何通過優化后處理,以鄰接矩陣V給定的簇態UV為目標,將本文提出的基于級聯四波混頻系統生成的四模糾纏態優化重構,最終生成三種不同結構的四模簇態.實數正交矩陣O(θ)有N(N-1)/2 個自由度可以選擇[46].特別地,對于四模態存在六個自由度.同時對角矩陣Ph有四個自由度.為了得到最優的正交矩陣O和對角矩陣Ph,用搜索算法尋找使矩陣O(θ)和Ph滿足簇態條件的最小nullifiers值[41],該算法特別適用于高維參數搜索.當nullifiers 值均低于散粒噪聲極限時,意味著四個輸出態存在量子關聯.然后根據van Loock和Furusawa[47]提出的連續變量多組份糾纏態的不可分判據,推導出滿足連續變量四模線型簇態的條件為

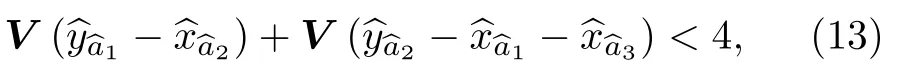
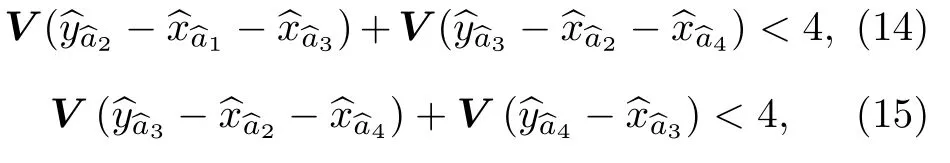
其中,這些不等式的左側和右側分別是nullifiers方差的組合和邊界條件.當左側的所有方差組合都小于 4 時,說明重構出連續變量四模簇態.該方法可以減小在有限的壓縮條件下生成簇態而引起的額外噪聲.如果所有的輸入模的壓縮值不相等,則此方法可以以最佳的方式重新分配模式之間的相關性.

對于四模糾纏態存在三種簇態結構,即線型、T-型和方型簇態.首先研究線型結構的簇態.令三個級聯四波混頻的強度增益相等,即G1.2,進而可以得到實際的壓縮值和反壓縮值: {—6.7 db,0 db,0 db,6.7 db}.利用優化算法找到滿足條件的正交矩陣O和Ph,實現線型簇態,結果如下:

經驗證結果滿足(8)式、(11)式和(12)式.Nullifiers的值分別為{1.174,1.87,1.783,1.386}.對于線型簇態,對應的散粒噪聲極限為{2,3,3,2}.因此歸一化后的Nullifiers 方差為{0.59,0.62,0.59,0.69},數值結果都小于1,說明低于散粒噪聲極限.根據Nullifiers 的結果,可以計算出不等式(13)式—(15)式左側方差的組合分別為: {3.04,3.63,3.15}.所有的組合結果都小于4,這意味著四模線型簇態可以由四波混頻系統生成的糾纏態通過優化后處理得到.同時研究了不同強度增益時的Nullifiers 值,結果列在表1 中.對于強度增益較小時,不同的強度增益應用優化算法均找到最優值使得Nullifiers的歸一化方差小于1,當強度增益為1.5和1.8 時,不等式(13)式—(15)式左側方差的組合分別為{3.04,3.12,2.42}和{2.58,2.97,2.09},Nullifiers 的方差組合都小于4,滿足van Loock-Furusawa 判據.

同樣的方法也可以研究T-型和方型簇態的變換情況,滿足連續變量四模T-型簇態的條件為

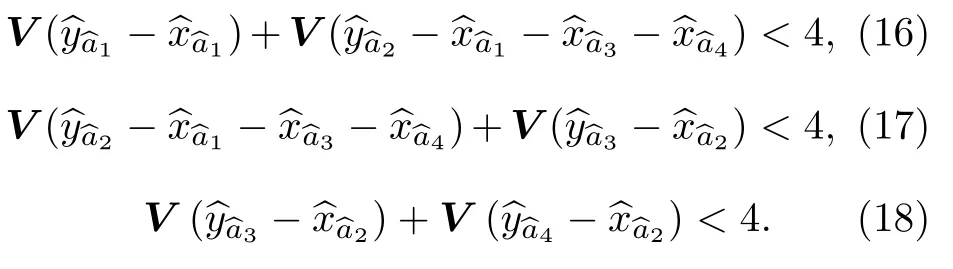
T-型簇態的散粒噪聲極限為{2,4,2,2},歸一化后的Nullifiers 方差如表2 所列.當強度增益為1.2,1.5和1.8 時,不等式(16)式—(18)式左側方差的組合分別為{2.42,2.5,1.96},{1.76,1.84,1.6}和{1.52,1.52,1.44},Nullifiers 的方差組合都小于4,滿足van Loock-Furusawa 判據.滿足連續變量四模方型簇態的條件為

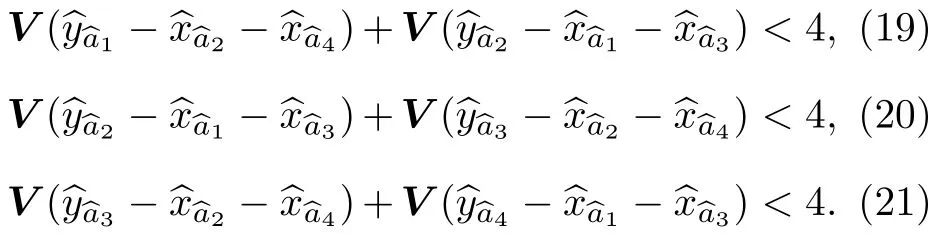
方型簇態的散粒噪聲極限為{3,3,3,3},歸一化后的Nullifiers 方差如表3 所列.當強度增益為1.2,1.5和1.8 時,不等式(19)式—(21)式左側方差的組合分別為{2.7,2.7,2.1},{1.65,1.65,1.86}和{2.34,1.74,3.06},Nullifiers 的方差組合都小于4,滿足van Loock-Furusawa 判據.結果表明當強度增益較小時,對于不同的強度增益,不同結構的簇態均可以找到相應的優化矩陣滿足簇態條件.這意味著基于級聯四波混頻過程生成的四模糾纏態,可以通過調控輸出光場的相位和后處理得到三種不同結構的簇態.但是對于強度增益較大時,應用此方法很難找到最優的變換矩陣使Nullifiers的歸一化方差小于1,結果如表1、表2和表3 中的最后一行所示.這與非對稱的級聯四波混頻系統輸出端的模式結構有關,強度增益很大時和在四個輸出模中占的相對權重逐漸變小并趨于0,和的相對權重逐漸變大并趨于1,這導致無法通過后處理轉換為簇態.

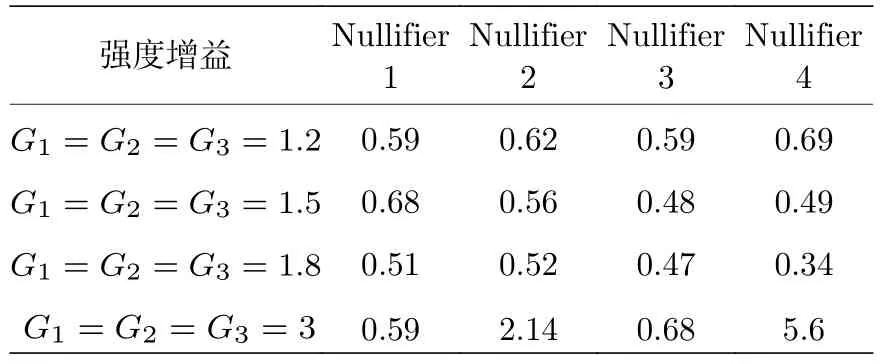
表1 對于不同的強度增益,四模線型簇態Nullifier 的歸一化方差Table 1.Normalized variances of the four-mode linear cluster state nullifiers for different intensity gains.

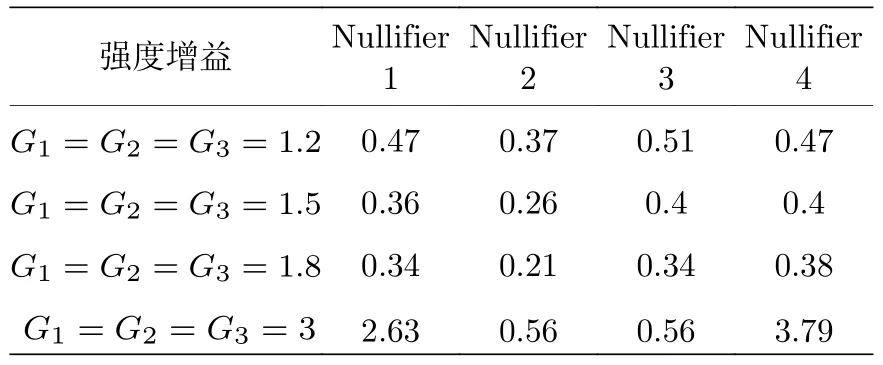
表2 對于不同的強度增益,四模T-型簇態Nullifier 的歸一化方差Table 2.Normalized variances of the four-mode Ttype cluster state nullifiers for different intensity gains.

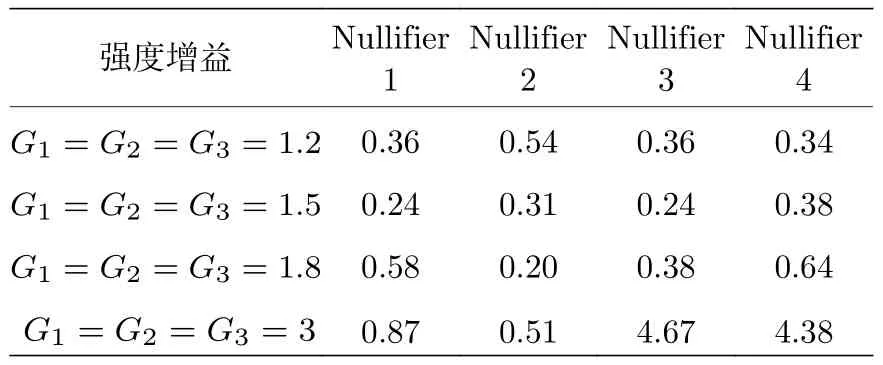
表3 對于不同的強度增益,四模方型簇態Nullifier 的歸一化方差Table 3.Normalized variances of the four-mode square cluster state nullifiers for different intensity gains.

4 結論

本文提出基于級聯四波混頻系統產生四模糾纏態的方案,并調控輸出態的相位和對噪聲信號后處理重構出三種不同結構的簇態.首先利用部分轉置正定判據證明該體系可以產生真正的四模糾纏態.然后分析四模糾纏態的本征模,發現該系統可分解為兩個單模壓縮態和兩個真空態.最后研究了不同強度增益下基于優化算法重構簇態的情況,并利用van Loock-Furusawa 判據判斷重構的態是否為簇態.結果表明在強度增益較小時,可以重構出線型、T-型和方型結構的四模簇態,強度增益很大時系統輸出端的雙模式結構影響生成四模簇態.這種基于級聯四波混頻過程重構不同結構簇態的多功能量子網絡平臺在量子計算和量子信息處理中存在潛在的應用.