基于線性生成圖編碼SoC測試向量方法

黃貴林，張正金，江家寶，吳其林，王洪海

(巢湖學院 信息工程學院，安徽 巢湖 238024)

0 引言

“芯片內集成的晶體管數目每18個月將增加一倍”，同時，系統級芯片和系統級封裝的產品，也稱片上系統(system-on-chip，縮寫為SoC)，已成為半導體產業的主要驅動力。單個芯片上集成的晶體管越來越多，給芯片測試帶來了一系列新的挑戰。其中，不斷增長的數據量測試是芯片測試必須面臨的挑戰[1]，在有限的ATE存儲空間和I/O帶寬方面，存儲和傳輸大量的測試數據，測試成本會升高，測試時間變長。測試數據壓縮技術一直致力于解決這個難題。

目前，測試數據壓縮技術分為三類[2]：基于LFSR結構的壓縮方法[3]、基于廣播掃描的壓縮方法[4]、編碼壓縮方法[5]。其中，編碼壓縮是一種十分受歡迎的測試數據壓縮方法，根據碼字的對應關系對數據塊進行編碼壓縮，如： GOLOMB、FDR、ALT-FDR、EFDR、9C、BM、RL-HC、SHC、VIHC，它們都是一些非常經典優秀的方案[6]。目前其能達到的壓縮效果還是非常理想的，但在測試應用時間上很難被接受，它以數據塊為單位產生測試數據，不能快速產生整條測試向量。為此，有通過加法器生成后續測試向量進行編碼壓縮的[7]。為考慮測試應用時間及壓縮率等問題，在測試向量層面，本文提出一種利用循環掃描鏈的測試向量編碼方法。該方法對所有測試向量進行順時針循環移位遍歷，找到所有間接相容的測試向量，并將其構造成線性生成圖。根據循環移動位置對測試向量進行編碼，編碼替換測試向量進行存儲，實現無損壓縮，達到測試數據壓縮的目的。本文貢獻：⑴解壓電路結構簡單。除了需要常規的FSM和計數器之外，只需要一個通道MUX即可。⑵測試數據壓縮率顯著提高。⑶測試應用時間大幅度降低。⑷算法簡單。

1 設計方案

1.1 循環掃描鏈

定義1：對于單掃描鏈而言，芯片測試外殼當中的所有掃描鏈是單方向的，是以串的形式連接在一起的。Input為時序電路的功能輸入(外部輸入)端，即測試向量的部分測試數據的輸入端，Output為時序電路的功能輸出(外部輸出)端，即測試響應的部分數據輸出端。每個觸發器的Q連接到時序電路當中組合電路的輸入端，也連接到下一級觸發器單元的Q′。

掃描鏈當中的第一個觸發器和最后一個觸發器連接起來，即最后一個觸發器的Q也作為第一個觸發器的輸入TD，如圖1所示，圖中虛線電路為本文添加的電路結構，與原有的觸發器連線，將所有觸發器連接形成一個環形的掃描鏈。測試向量可以在掃描鏈當中順時針循環移動，因此稱為循環掃描鏈。

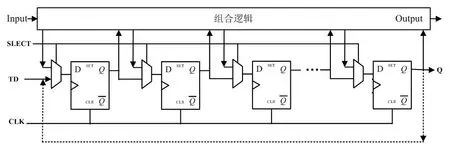
圖1 循環掃描鏈

定義2：物理上形成的循環掃描鏈，測試向量可在循環掃描鏈當中順時針循環移動。邏輯上，就形成了環形的循環測試向量。測試向量1：A0、A1、A2、…、An，測試向量2：B0、B1、B2、…、Bn，測試向量1和2的對應位A0和B0、A1和B1、A2和B2、…、An和Bn等對應位全部相容，則稱測試向量1和測試向量2直接相容。

圖2 測試向量1在掃描鏈中循環右移1位

如圖2所示，測試向量x0011在循環掃描鏈當中順時針循環移動1位，得到測試向量1x001。測試向量1x001與圖3當中的測試向量2(1xx01)相容，則稱測試向量1與測試向量2間接相容。下劃線所示的兩個測試位1和1，是新形成的對應位。

圖3 測試向量2

1.2 線性生成圖

在邏輯上，每個測試向量都是循環測試向量。先探索構造環形生成圖，節點是測試向量，所有節點的出度和入度都為1，N個節點共有N條邊。再繼續構造線性生成圖，首節點的出度為1，尾節點的入度為1，其余每個節點的出度和入度都為1，N個節點共有N-1條邊。節點之間間接相容，循環右移的位數為權值。測試向量長度為L。

⑴列表List1的初始狀態是空集，列表List2的初始狀態包含整個測試集，即被測電路的所有測試向量。

⑵第0個測試向量T(0)從List2進入List1，List2中沒有T(0)。在(3)到(7)中，List1和List2的并集是被測電路的整個測試集，即被測電路的所有測試向量。

⑶測試向量的長度為L，測試向量T(1)順時針循環移動n位，然后第n位，第(n+1)位，…，第(L-1)位、第0位、第1位、…以及循環測試向量T(1)的第(n-1)位，分別與循環測試向量T(0)的第0位、第1位、第2位、…、第(L-2)位、第(L-1)位形成新的對應位關系，對T(0)和T(1)之間不相容的位數進行計數。n的范圍在0和L-1之間。根據不同的n，統計L次T(0)和T(1)之間不相容的位數。在這個統計過程中，如果不相容位的最小個數為0，說明T(0)和T(1)之間間接相容，那么T(1)從List2進入List1。

⑷重復這個過程，即List1中的任意一個測試向量T(i)和List2中的某個測試向量T(j)之間相容性分析的過程。如果T(i)與T(j)間接相容，那么T(j)從List2進入List1。

⑸如果List1中的任何測試向量與List2中的任何測試向量不間接相容，則選擇List1中的任何測試向量T(k)以循環向右移位。當T(k)每次向右移位一位時，判斷是否間接相容其他測試向量。如果首先發現T(m)與T(k)間接相容，那么將T(m)設為T(k)的鄰節點。T(m)將從List1中刪除。

圖4 環形生成圖

圖5 線性生成圖

⑹重復(5)直到List1是一個空集。最后一個測試向量T(n)成為T(k)的相鄰節點，形成與表1對應的環形生成圖，如圖4所示。

⑺刪除權重最大的邊，構造有向線性生成圖，如圖5所示。在測試過程中，會按照有向線性生成圖的順序生成測試向量，種子測試向量T7會生成測試向量T1，T1會生成T3，以此類推，直到生成T5，所有的測試向量都會生成。

1.3 編碼實例

現有9個測試向量，每個測試向量為40位，9個測試向量之間全部間接相容。第一個測試向量T1每次循環右移1位，查找是否存在測試向量與其間接相容，如圖4所示。

表1 測試向量相容性分析

在T1循環右移2位時發現，新形成的測試向量與T3最先相容，T1與T3間接相容。因此，T3編碼為10010。

T3繼續循環右移，當循環右移3位時發現，新形成的測試向量與T8最先相容，T3與T8間接相容。因此，T8編碼為10011。

以此類推，T6、T9、T2、T4、T5、T1分別編碼為10001、10100、10110、11000、10101 和 10010，如表1所示。刪除權值最大的邊，得到圖5，將測試向量T7作為種子測試向量。在測試過程中，將按照圖5所示順序生成后續測試向量。

按照圖5所示線性生成圖的順序，T7循環右移產生T1，T1產生T3，直至產生T5，循環右移位數之和為31，即如圖5所示權值之和為31，小于測試向量長度。總的來說，生成圖所有測試向量的測試應用時間長度與單個測試向量長度值相當，單個測試向量的測試應用時間長度遠小于測試向量長度值。

2 解碼體系結構

本方案的解壓體系結構主要是由FSM、計數器1、計數器2、計數器3和MUX構成。如圖6所示，‘en’和‘bit_in’分別是輸入使能和位輸入信號。‘flag’為MUX通道選擇信號，‘data_in1’和‘data_in2’連接MUX兩個輸入端，MUX輸入端‘data_in2’連接掃描鏈的末端，MUX輸出端‘out’連接掃描鏈的頭部。MUX控制掃描鏈觸發器當中的測試數據在掃描鏈內部順時針循環移動，得到新的測試數據，即產生下一個測試向量。

圖6 解壓結構

計數器1用于測試向量移入掃描鏈計數。‘dec1’用于計數器1減1，‘rs1’用于指示計數器1的復位0狀態，計數器1的長度為┌log2(L)┐。計數器2用于編碼code移入暫存器計數。‘dec2’用于計數器2減1，‘rs2’用于指示計數器2的復位0狀態，計數器2的長度為┌log2(code_L)┐，code_L為編碼長度。

計數器3用于順時針循環移位時鐘周期數計數，即為循環移位位數計數。‘dec3’用于計數器3減1，‘Dec3’用于指示將暫存器中的編碼重置至計數器3，‘rs3’用于指示計數器3的復位0狀態，┌log2(code_L)┐為計數器3的長度。暫存器里存放的是編碼，‘dec’用于使能暫存器，‘data_in’用于將編碼code移入暫存器。

3 編碼分析

N個測試向量構造線性生成圖，構造環形生成圖的時間復雜度T(L)=O(N×L)，構造線性生成圖的時間復雜度T(L)=O(L)，則整個算法時間復雜度為O(L)，算法簡單。壓縮率為：

很顯然，對于環形生成圖，權值之和為L，對于線性生成圖，權值之和小于L。除種子測試向量，線性生成圖上的測試向量測試應用時間時鐘周期數為t。

4 實驗結果

為證明本方案在壓縮率上的有效性，給出了基于國際公認的ISCAS89標準電路的實驗結果。在實驗過程中，測試向量被連續注入編碼算法。圖7至圖12是不同情況下的壓縮率變化曲線，橫坐標表示注入算法的測試向量X的數量，縱坐標表示壓縮比Y。由測試圖可知，在測試向量注入過程中，壓縮率波動，但是總體壓縮率保持上升趨勢。因此，本文提出的測試數據壓縮方案具有魯棒性，符合公式⑵的預期。

為進一步證明本方案的有效性和科學性，計算標準電路測試向量的總體壓縮率，如表2所示。最后一列為本文所提方案的壓縮率，壓縮率優于其他的大部分方案，平均壓縮率都優于其他方案，說明本文所提方案適應性較好。

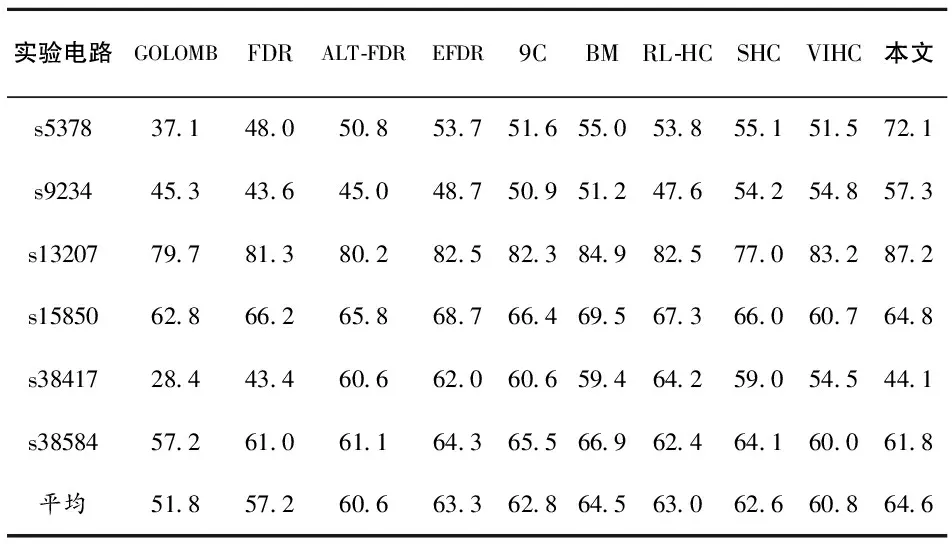
表2 實驗結果

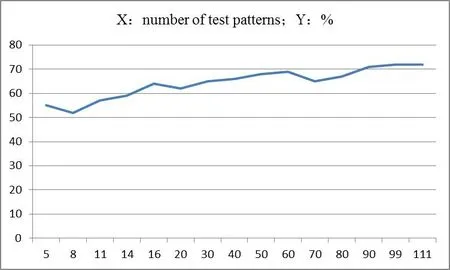
圖7 S5378壓縮率變化曲線

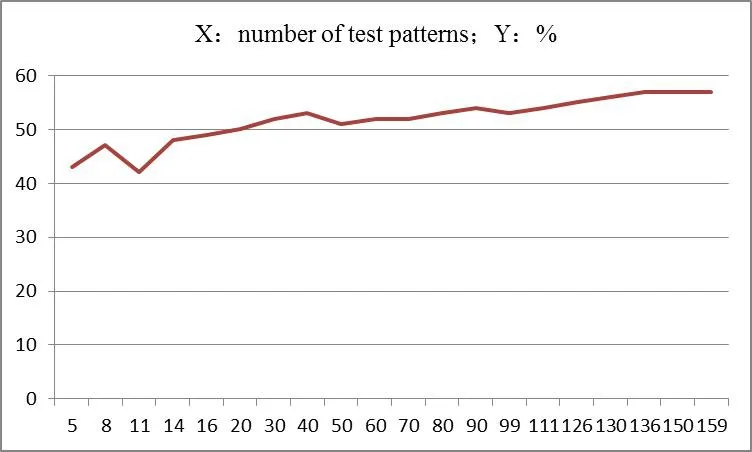
圖8 S9234壓縮率變化曲線

圖9 S13207壓縮率變化曲線

圖10 S15850壓縮率變化曲線

圖11 S38417壓縮率變化曲線

圖12 S38584壓縮率變化曲線

5 結論

本文主要是探索測試向量之間的相容性，通過順時針循環右移掃描鏈當中的測試向量錯開對應位，原對應位之間的位置關系已經不再對應了。測試向量當中存在大量無關位，新形成的所有對應位存在全部相容的可能性，使得不同的測試向量之間存在間接相容的關系，消除了這種原對應位不相容的問題，為測試數據壓縮提供了依據，有效降低測試應用時間。