大型組塊浮托安裝的對接分析

王彥多，劉建峰，葉永坤，于志強

(海洋石油工程股份有限公司,天津 300461)

隨著海洋石油工業和海洋工程技術的迅速發展，我國海洋工程已逐步由淺水邁向深水海域，海洋平臺正朝著綜合化、復雜化、大型化方向發展。海洋平臺組塊整體重量從幾百噸增加到上萬t，目前國內最大安裝組塊已重達32 000 t。由于受浮吊船最大吊裝能力的限制及大型組塊分塊吊裝有諸多不利因素的影響，將有越來越多的大型組塊采用浮托安裝。

在海況相對較好的渤海海域，在浮托安裝組塊過程中，組塊腿柱與導管架腿之間的相互碰撞力一般不大，對接工況多不是組塊結構強度設計的控制工況；在海況相對惡劣的南海海域，在浮托安裝組塊過程中，組塊腿柱與導管架腿之間的相互碰撞力較大，對接工況往往是組塊結構強度設計的控制工況。但是，如果對組塊浮托安裝過程對接分析保守計算的話，則會造成組塊結構強度設計過強，用鋼量過大，增加成本。為此，以南海某海洋平臺組塊浮托安裝過程中對接分析為實例，采用海洋工程行業常用的SACS計算軟件，對接分析計算方法。

1 對接工況介紹

1.1 對接過程

在海上采用浮托安裝法安裝組塊的過程一般分為3個主要階段：駁船進船階段(DOCKING)、組塊與導管架對接階段(MATING)和駁船退船階段(UNDOCKING)。其中，組塊與導管架對接過程，是指駁船運載組塊進入導管架槽口后，切除組塊支撐結構DSF與組塊間的裝船固定結構(拉筋和筋板等)，利用潮汐和駁船調載等實現對組塊的升降，同時輔以對接耦合裝置LMU(保證浮托安裝成功的關鍵部件，用于減緩組塊和導管架間的相互沖擊，可預安裝在組塊腿柱上，也可預安裝在導管架腿上)，然后將組塊重量從駁船上分階段轉移到導管架腿上的過程，如圖1所示。

圖1 組塊與導管架對接示意

1.2 荷載轉移

荷載轉移是對接工況中最核心的部分，在荷載轉移過程中，導管架、LMU、組塊、DSF和駁船之間相互耦合，整個過程十分復雜。為了便于進行數值模擬，在對組塊結構強度進行對接分析時(見圖2)，通常將對接工況中的荷載轉移分為5個主要階段。第1階段是0%的組塊荷載轉移到導管架上；第2階段是25%的組塊荷載轉移到導管架上；第3階段是50%的組塊荷載轉移到導管架上；第4階段是75%的組塊荷載轉移到導管架上；第5階段是100%的組塊荷載轉移到導管架上。

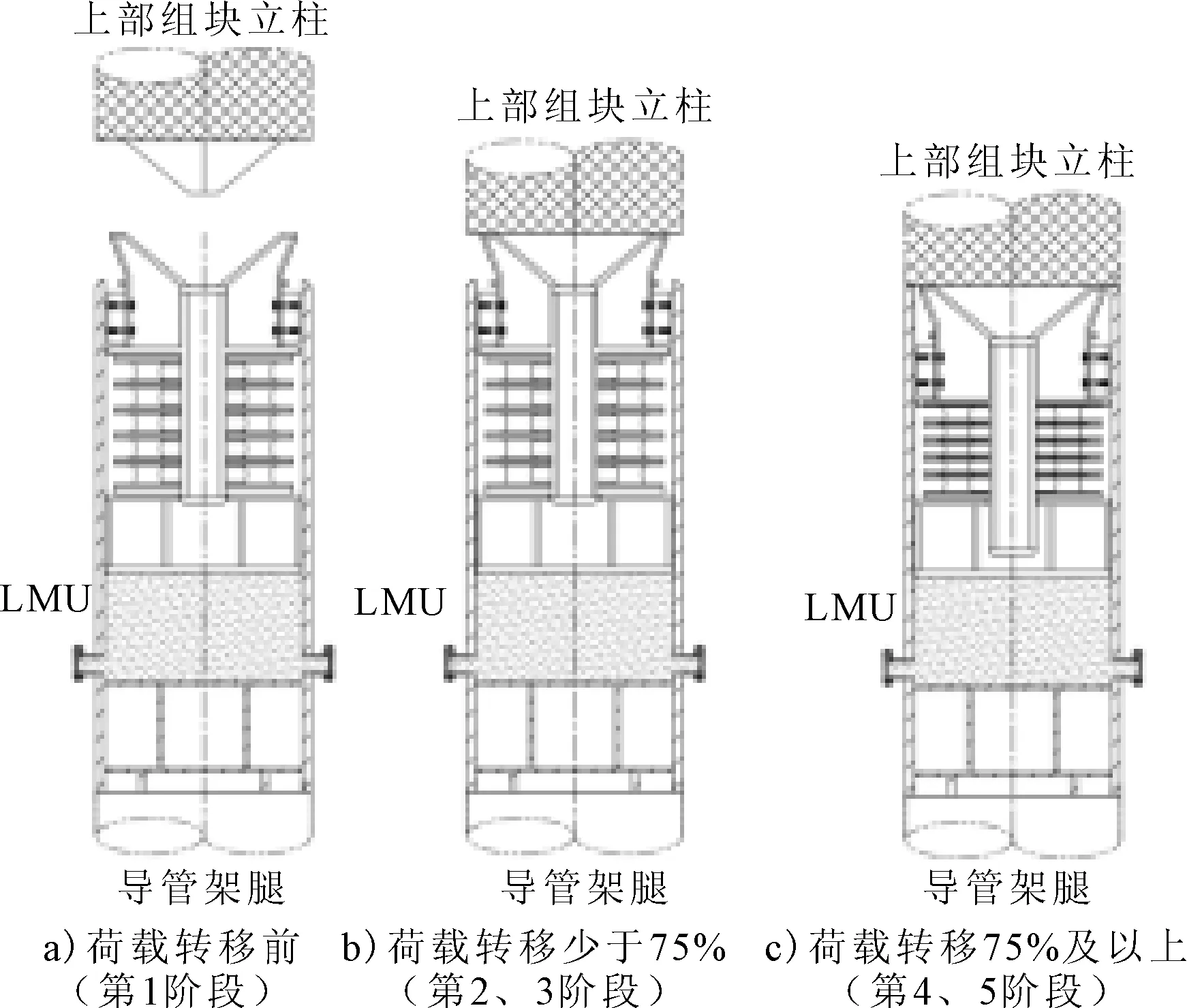
圖2 荷載轉移示意

1.3 碰撞力

在組塊荷載轉移的過程中，由于受風浪流的影響，駁船在橫搖、縱搖和升沉等運動過程中，組塊腿柱底端插尖與導管架腿頂部的LMU會不斷發生相互碰撞，從而使組塊腿柱底端承受較大的碰撞力。通過數值模擬和實際工程監測統計數據可知，在荷載轉移的第4、5階段的水平碰撞力通常都大于第1、2、3階段的水平碰撞力。

如圖3所示，在組塊荷載轉移的過程中，在A2.1、A2.3、B2.1和B2.3軸上4根分離緩沖裝置DSU不會直接承受碰撞力，但是在A1～B4軸上8根組塊腿柱底端，都會承受水平方向和豎直方向上的碰撞力，即在組塊對接分析SACS計算模型的整體坐標系中，每根組塊腿柱底端在這3個對應方向上都分別承受3個碰撞力分量：、和。在對組塊結構強度進行對接分析時，上述每根組塊腿柱底端承受的碰撞力，都可以從浮托安裝過程中浮體運動分析的計算結果中提出。

圖3 組塊腿柱承受碰撞力示意

2 對接分析方法

2.1 設計基礎

1)組塊對接分析SACS計算模型如圖4所示，除了不包含DSF和裝船固定用結構外，其與組塊運輸分析SACS計算模型基本一致。

圖4 組塊對接分析SACS計算模型

2)組塊對接分析SACS計算模型的重控與組塊運輸分析SACS計算模型的重控基本一致。

3)對接分析不考慮風荷載對組塊結構強度的影響。

4)根據AISC規范和API規范，在對接分析時鋼材的屈服強度被放大了1.333倍。

2.2 荷載組合

2.2.1 基本荷載

對接分析的基本荷載主要包括組塊重量WTD和碰撞荷載。其中，在組塊對接分析SACS計算模型中，對應于上述荷載轉移的5個主要階段，根據浮體運動分析MOSES計算結果提供的碰撞力，按照0°～315°共8個方向共計40組碰撞荷載可以被分別定義為C11～C58，見表1。

表1 碰撞荷載

2.2.2 組合荷載

對接分析的組合荷載主要是將WTD與40組碰撞荷載C11～C58進行一一組合，40個組合荷載被分別定義為WF11～WF58，見表2。

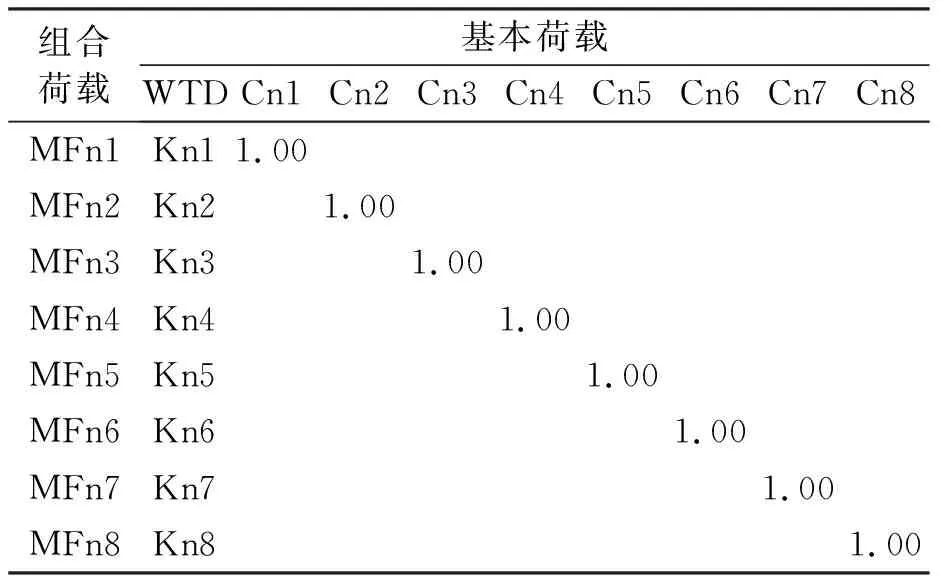
表2 第n階段組合荷載

在表2中，對應于荷載轉移的5個階段，分別取=1、2、3、4、5。

由表2可知，組合荷載MF11=WTD×K11+C11×1.00，其他的組合荷載可由此類推。其中，Kn1～Kn8分別表示K11～K58這40個WTD的組合系數，一般取1.00；但是當某個Cnn的豎向碰撞力大于WTD時，則對應的Knn應取一個大于1.00的系數來平衡豎向碰撞力，以避免DSU節點處出現受拉工況。

2.3 邊界條件設置

2.3.1 傳統方法

在組塊浮托安裝對接分析時，從第1階段至第5階段的整個對接過程中，傳統方法對組塊對接分析SACS計算模型的邊界條件作如下設置。如圖5所示，A2.1、A2.3、B2.1和B2.3軸上DSU單元底部節點的約束形式都被模擬為鉸接(111000)；而A1～B4軸上8根組塊腿柱的底端節點都是自由的。

圖5 邊界條件設置傳統方法示意

2.3.2 傳統方法存在的問題

由上述可知，傳統方法認為在整個對接過程中組塊腿柱底端都沒有約束，這與LUM設計性能和變形特點完全不符。通常情況下，LUM吸能裝置最大承受的設計載荷是75%的組塊重量，當大于等于75%的組塊荷載轉移到LMU上面之后，LUM中的接收器和垂向橡膠單元都被完全壓縮至LMU筒體內不再繼續發生彈性變形，此時導管架腿連同LMU筒體對組塊腿柱底端產生較大的約束作用，從而改變了組塊腿柱底端的自由度，造成組塊腿柱底端不再是自由的。因此，邊界條件設置的傳統方法中在第4階段和第5階段，組塊腿柱底端仍然沒有約束，與組塊浮托安裝過程的實際情況不符。

一般而言，在進行海況條件相對較好且組塊重量相對較輕的浮托安裝設計時，對接工況往往未成為組塊結構強度設計的控制工況；而對海況條件相對惡劣的大型組塊浮托進行安裝設計時，對接工況通常會成為組塊結構強度設計的控制工況；如果再按照傳統方法進行邊界條件設置，會造成對接分析過于保守，從而組塊結構設計過強，用鋼量過大。

2.3.3 改進方法

由邊界條件設置的傳統方法可知，在對接過程中的第1個階段、第2個階段和第3個階段，組塊腿柱插尖還未完全進入LMU的接收器內，使得LMU接收器和垂向橡膠單元還未被完全壓縮變形，對這三個階段對應的24個組合荷載進行計算分析時，可以將組塊腿柱底端設置為自由端，如圖5所示。但是，在第4階段和第5階段，LMU接收器和垂向橡膠單元被完全壓縮到LMU筒體內，組塊腿柱受到LMU筒體的豎向支撐和水平約束。對第4階段和第5階段中MF41～MF58這16個組合工況進行計算分析時，不應再將組塊腿柱底端按自由端設置，而應考慮LMU筒體對8根組塊腿柱底端的約束。

此外，雖然對接過程中組塊腿柱與導管架腿之間的碰撞力較大，但是這些碰撞力對組塊腿柱和導管架腿而言所產生的碰撞變形通常都是在彈性范圍之內。因此，對接分析組塊SACS計算模型的邊界條件設置的改進方法，是在第4階段和第5階段將8根組塊腿柱底端分別在方向和方向上設置線性彈簧單元，用來等效模擬LMU筒體對8根組塊腿柱底端的水平約束，見圖6。

圖6 邊界條件設置改進方法示意(第4、5階段)

2.4 線性彈簧剛度計算

由圖1可知，在組塊浮托安裝之前，LMU筒體已焊接固定在導管架腿頂端，因此在對接過程中LMU筒體對組塊腿柱底端的約束，實際上就是導管架腿和LMU筒體整體對組塊腿柱的約束。在8根組塊腿柱底端SACS計算模型中所設置的線性彈簧單元的剛度，與導管架腿連同LMU筒體整體在位時LMU筒體頂端的剛度等效。

因此，針對SACS模型中組塊某根腿柱底端方向或方向所設置線性彈簧剛度的計算，可根據導管架和LMU筒體整體在位的SACS模型，在對接點處(LMU筒體頂端)加載一個水平單位荷載(一般取=1 000 kN)，通過在位分析從而計算出該節點在水平單位荷載對應方向上的位移，如圖7所示，則水平荷載與位移的比值(單位通常取kN/m)就是導管架連同LMU筒體整體結構在該節點對應方向上的剛度，即為對應線性彈簧的剛度。以上只是以其中一個線性彈簧剛度的計算為例，其余15個線性彈簧剛度計算方法與其相同。

圖7 導管架腿頂端剛度計算示意

3 對接分析結果

3.1 桿件應力比

如表3所示，根據相關規范規定在已考慮組塊鋼材屈服強度擴大1.333倍的前提下，當邊界條件設置采用傳統方法時，對接分析結果中有5根高1 500 mm主梁(表3中記為①)、2根高1 800 mm主梁(記為②)和2根直徑610 mm斜撐(記為③)的應力比大于1.000，不滿足規范要求；當邊界條件設置采用改進方法時，上述桿件的應力比最大為0.885，滿足規范要求。

表3 傳統方法與改進方法主要桿件應力比的結果對比

3.2 節點沖剪應力比

對于8根組塊主立柱與其斜撐相交的16個主節點的沖剪校核，邊界條件設置傳統方法與改進方法節點沖剪應力比的結果對比見表4，雖然兩種邊界條件設置方法的節點沖剪應力比相差不大，但是在這16個主要節點中，有13個節點采用傳統方法的沖剪應力比大于采用改進方法的沖剪應力比。可見在節點沖剪校核方面，傳統方法的結果相對保守。

表4 桿件直徑為2 000 mm時兩方法主要節點沖剪應力比對比

4 結論

由對接分析邊界條件設置傳統方法和改進方法的計算結果對比可知，傳統的邊界條件設置方法的計算結果相對保守，往往會造成組塊結構強度設計過強，用鋼量過大，增加成本；而邊界條件設置改進方法算出的主桿件應力比和主節點沖剪應力比相對較小，且該計算結果的安全性已得到工程實踐的驗證。因此，采用改進的邊界條件設置方法進行對接分析，可為大型組塊結構強度控制和結構重量控制提供設計依據，可為今后類似項目的設計分析提供參考。