基于支持向量回歸的葉片擠壓出料溫度預測研究

戴南，余心宏，郭佳鑫，余齊嚴

基于支持向量回歸的葉片擠壓出料溫度預測研究

戴南1，余心宏1，郭佳鑫1，余齊嚴2

（1.西北工業大學 材料學院，西安 710072；2.西安翔迅科技有限責任公司，西安 710068）

針對傳統葉片精鍛過程中存在的質量波動較大的問題，提出一種預測傳統葉片精鍛質量的方法。以GH4169轉子葉片精鍛的擠壓工序為研究對象，以葉片精鍛擠壓過程中的160組模擬結果為數據集（以其中的120組數據為訓練集、其余40組數據為測試集），對截面點的出料溫度進行預測。首先利用特定的數據預處理手段及特征工程提升模型的預測精度及泛化能力，建立SVR預測模型，然后基于網格搜索算法和粒子群優化算法（GS–PSO）對預測模型中參數和進行調節，得到優化后的模型，最后將測試數據集帶入優化后的模型中，將預測值與真實值進行對比。單一的SVR模型預測效果不佳，利用GS–PSO算法優化后，模型自適應度由0.007 8左右降到0.005 2左右，模型收斂快且優化效果顯著。30顆粒子迭代50次的最終優化結果為：=425.432 8，=1.883 2，模型優化后的預測值與實際值之間擬合度較好，每組數據的預測誤差都遠小于10%。經GS–PSO優化的出料溫度SVR預測模型在測試集中有較好的預測效果，滿足行業數據預測要求的一般標準，對傳統葉片精鍛過程指標預測具有較好的參考意義。

葉片精鍛；擠壓；數據挖掘；質量預測

隨著互聯網和信息化等大數據科學技術的進步和迅猛發展，數據挖掘在產品質量控制、生產過程監控等方面逐漸得到了應用并取得了一定成果。葉片是汽輪機、航空發動機的核心部件之一，在精鍛過程中可能產生葉片厚度尺寸不穩定、表面質量差、榫頭晶粒差和力學性能差等質量問題[1]，在葉片精鍛過程質量管理方面還存在生產過程信息化程度低、過程數據信息挖掘不足、葉片質量控制手段匱乏等一系列問題[2-3]。目前，多采用對成品葉片外形尺寸及冶金質量進行抽檢的方式對葉片的質量進行控制，采用紙質記錄的方式記錄葉片擠壓過程中的出料溫度[4]，這些方式具有一定的滯后性。在鍛造過程質量控制方面，Allam[5]開發了一個決策支持系統來改進鍛造生產過程，該系統可以將產品規范或鍛造規范與工藝參數關聯起來。Hawryluk等[6]利用傳感器和服務器構建了一個能夠連續監測（測量、存檔和分析）鍛造參數（打擊力、模具溫度等）的測控系統。酆亞楠等[7]通過劃分鍛造車間數據，提出了一種利用工業以太網全局聯通整個車間，完成各車間生產數據的連接傳輸并提供多類數據的采集方法。曾琦[8]成功構建了曲軸鍛造生產的智能鍛造系統，并設計了系統的架構和各項具體功能，通過對曲軸鍛造智能感知技術和檢測方法進行研究，進而從分析評價曲軸鍛件質量的角度來控制曲軸鍛件質量。

文中著眼于塑性成形生產的智能化發展，以GH4169葉片擠壓過程的質量指標——出料溫度為研究對象，建立基于支持向量回歸（SVR）的GH4169轉子葉片精鍛的擠壓出料溫度預測模型，并將網格搜索（GS）和粒子群優化（PSO）算法相結合構成GS–PSO算法，用以優化預測模型的參數，進而預測葉片精鍛擠壓工序的出料溫度。

1 原理與方法

1.1 支持向量回歸

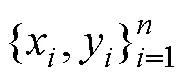
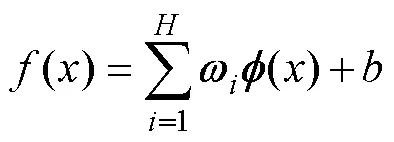
(2)

式中：為不敏感值。

SVR的核心在于找到最合適的|(·)使式（3）中()取最小值。

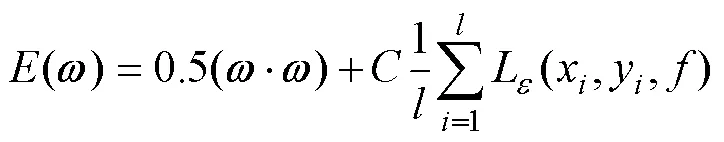
式中：()是由幾何間隔為簡化計算而變換成的目標表達式；為數據樣本擬合精度函數和回歸模型復雜度的加權計算結果；為訓練數據樣本數。

利用非負松弛變量ξ和ξ'可獲得與式（3）等價的對偶問題，如式（4）所示。

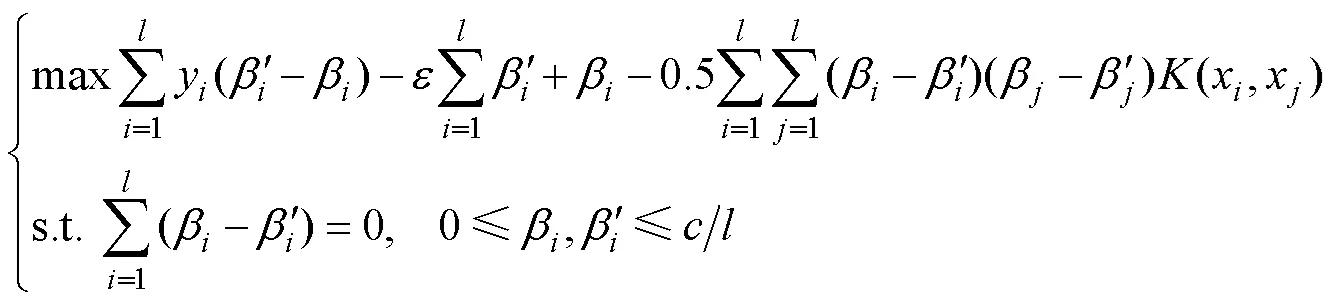
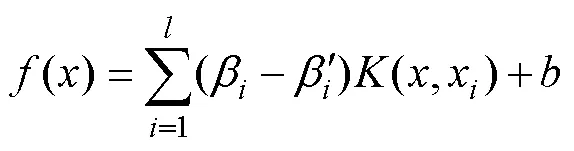
1.2 網格搜索算法

網格搜索（grid search，GS）算法是通過循環遍歷參數的每一種可能結果，將各種參數窮舉組合，以獲得具備最優評估效果參數組合的一種算法。例如文中基于SVR的葉片擠壓出料溫度預測模型，在使用徑向基函數（radial basis function，RBF）選取模型參數和參數的最優取值范圍時，利用網格搜索算法使每個參數組合在一起，在取值范圍內組成網格遍歷從而獲取了最優參數。該算法在參數范圍小、樣本小的情況下具有一定優勢，但運算效率較低。

1.3 粒子群優化算法

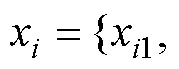
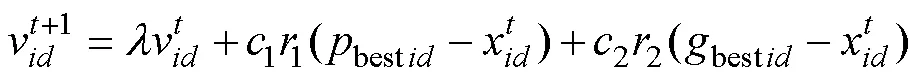
式中：為目前的迭代次數；為慣性權重；1、2為學習因子；1、2為（0,1）隨機數；best和best分別為個體最優位置和種群最優位置。

適應度函數值是PSO最優解搜索過程中最優位置的評價標準，因此選擇合適的適應度準則函數尤為關鍵。

2 GS–PSO優化的葉片擠壓出料溫度SVR預測模型

2.1 影響葉片擠壓過程出料溫度的因素

轉子葉片精鍛過程主要由下料、擠壓、預鍛、終鍛、冷切邊和熱處理幾個工序構成，其中擠壓是首次成形的制坯工序，擠壓件的尺寸及晶粒大小等質量指標對葉片成品而言尤為關鍵，擠壓件不同部位的出料溫度能表征擠壓件的晶粒質量。在葉片擠壓過程中影響出料溫度的因素眾多，主要包括工藝參數及設備模具參數，工藝參數包括葉片的坯料尺寸、坯料溫度、壓下速度及轉移時間等，設備模具參數包括模具號、模具間隙、入模角、玻璃涂覆量等。

2.2 數據獲取

文中采用DEFORM–3D軟件對該葉片預制坯擠壓過程進行模擬，通過模擬實際生產中各類參數的波動變化情況獲得了160組數據。對尺寸為26 mm× 35 mm的GH4169合金棒料加熱到1 020 ℃，采用水基石墨潤滑劑潤滑模腔并加熱到300 ℃，對滑塊壓下速度為20～50 mm/s的過程進行多組模擬，DEFORM– 3D模具示意圖以及溫度分布圖如圖1和圖2所示。

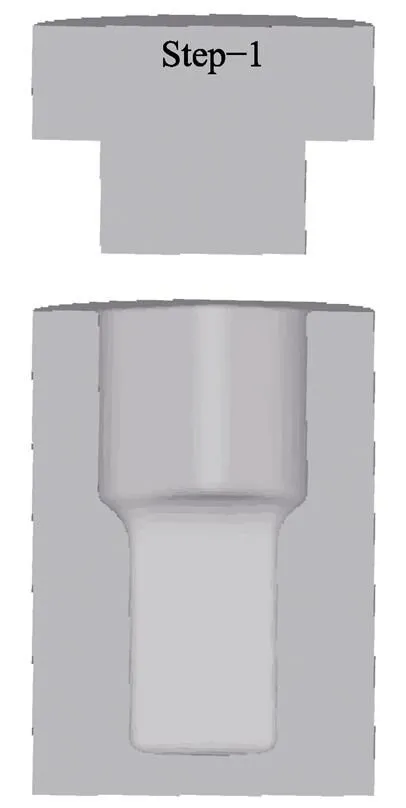
圖1 模具模型示意圖

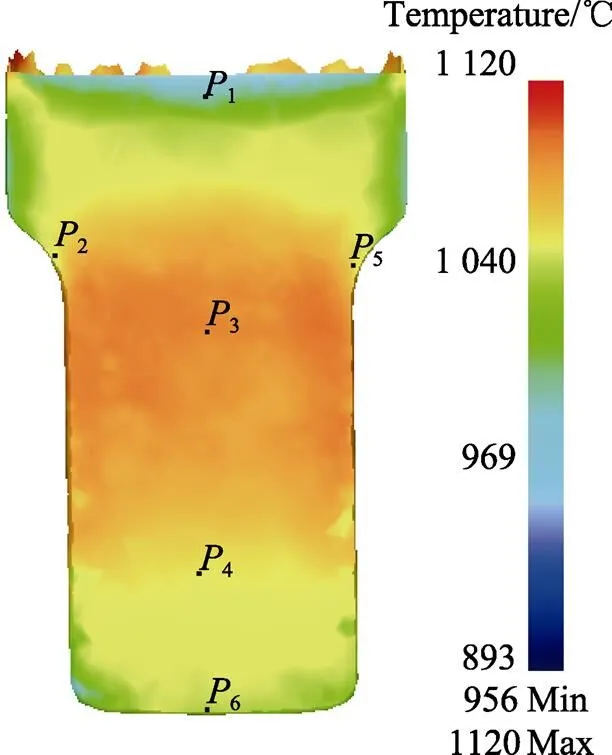
圖2 溫度分布云圖

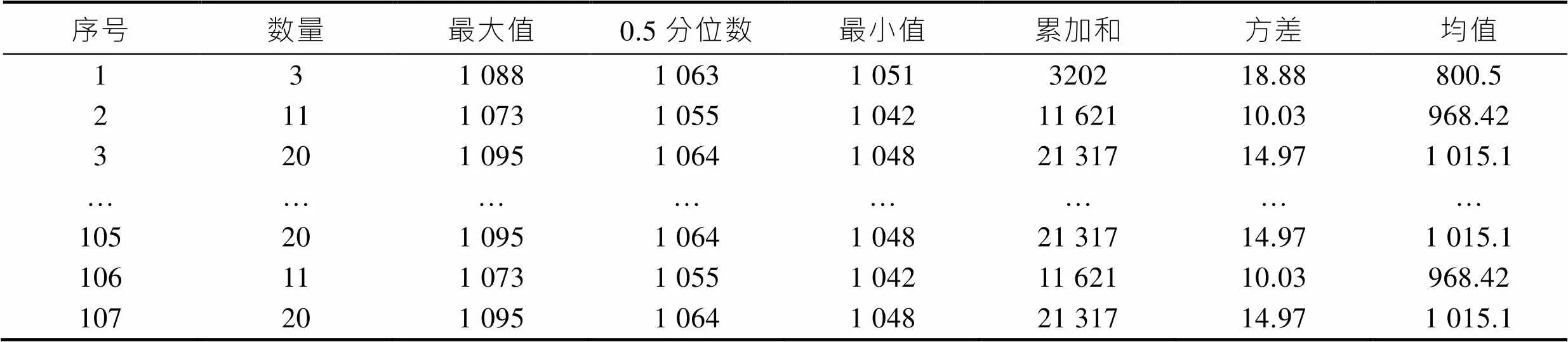
不同截點的出料溫度分布情況見圖2。為了更接近實際生產數據，模擬時所有工序參數的輸入應該在設定范圍內隨機波動，例如坯料長度在（35±0.5） mm范圍內波動，坯料溫度在980～1 050 ℃間波動，模具間隙在0.1～0.3 mm間波動，模具溫度在250～320 ℃間波動等。所獲得葉片模擬數據如表1所示。

2.3 擠壓出料溫度SVR預測模型的構建

2.3.1 數據預處理及特征工程

以構建2截點出料溫度預測模型為例，擠壓數據集中包含可能影響出料溫度的15個自變量因素，以出料溫度為響應變量。按照先后順序從葉片加工數據集中挑選出120組加工數據作為訓練集、40組加工數據作為測試集進行機器學習，建立出料溫度的預測模型。

表1 葉片模擬輸出數據集

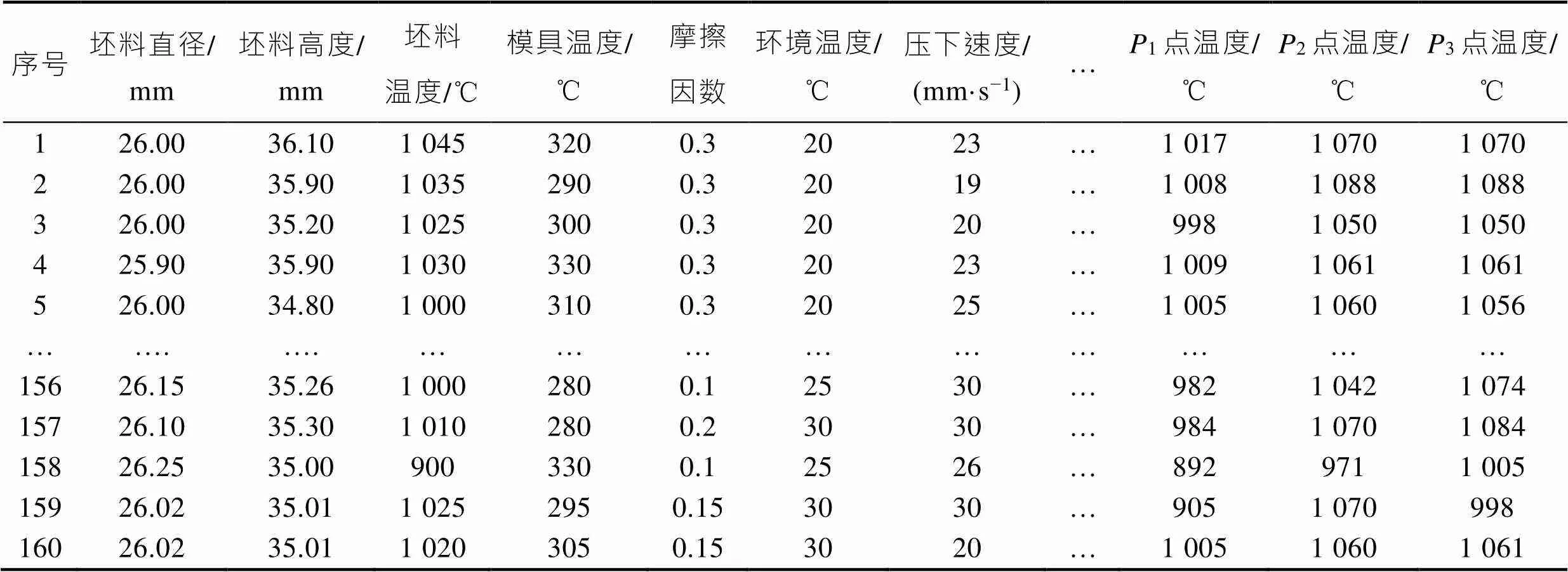
Tab.1 Blade analogy output datasets

文中利用Python 3.7中NumPy和Pandas工具包對數據進行預處理，采用直接刪除整行的方式將數據中噪聲數據的異常值和空缺值進行剔除。通過計算每一項特征數據的分位數進而得到上下限來剔除數據匯總的異常值，數值位于上下限外的數據利用箱線圖剔除，其中上下限的計算見式（8）—（9）。

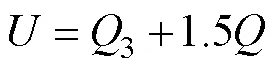
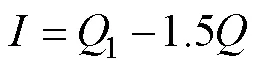
式中：為上限值；為下限值；3為上四分位數；1為下四分位數；為四分位數間距，=(3?1)，其中為常數（根據數據規模而設定）。

在刪除異常值和空缺值后，訓練集剩下107組數據，測試集剩下34組數據。針對SVR模型還需要對訓練樣本和測試樣本進行標準化處理，標準化的本質是線性變換，在變換的同時不會造成“失效”并能增強預測效果，常用變換公式見式（10）。

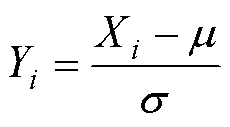
式中：Y為標準化后的新序列；X為標準化前的序列；和分別為標準化前序列的均值和方差。

在對數據進行預處理和標準化后，再對葉片加工數據集進行特征工程處理。特征工程能提高預測模型的上限，增強模型的預測效果。對預測出料溫度的數據集進行多次試驗，發現經過以下特征工程處理能顯著提升預測效果：（1）構造新的特征，在原數據集上，用與出料溫度相關性較大的因素如坯料溫度來構造新的特征，利用坯料溫度對出料溫度進行分組來構造如數量、最大值、最小值、均值、方差、中位數等基本統計量，將統計量作為新的特征加入數據集，加入的特征如表2所示；（2）數據分桶，數據分桶是一種用于減少次要觀察誤差影響的數據處理技術，在本數據集中可將壓下速度（）的數值進行等頻數據分桶，即在原有壓下速度特征基礎上將速度分為10個頻段，來提升擬合效果；（3）One–Hot編碼，對于某些如模具間隙、棒料圓角等數值種類較少的特征，可利用One–Hot編碼映射其數值，用二進制來表示圓角和間隙，能提升數據的維度并優化模型的距離計算。

表2 數據集中新加入的統計量特征

Tab.2 Characteristics of newly added statistics in the dataset

2.3.2 預測模型的構建及性能評價

將經過數據預處理及特征工程處理的訓練集數據代入SVR模型中，并利用RBF作為核函數進行模型訓練，獲得預測2點出料溫度的模型。為了更加準確地識別模型的性能，文中利用五折交叉法驗證模型的平均絕對誤差（mean absolute error，MAE）評價準則來判斷訓練集的預測精度，其計算公式如式（11）所示。

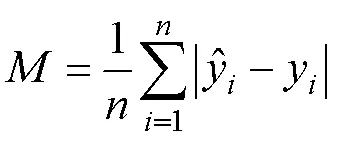
式中：為預測結果；yi為觀測值；M為平均絕對誤差。計算可得107組訓練集模型預測結果的M值為0.012，預測效果較理想。考慮預測模型的泛化能力，作出SVR模型的學習驗證曲線和測試集預測溫度數值折線圖，分別如圖3和圖4所示。

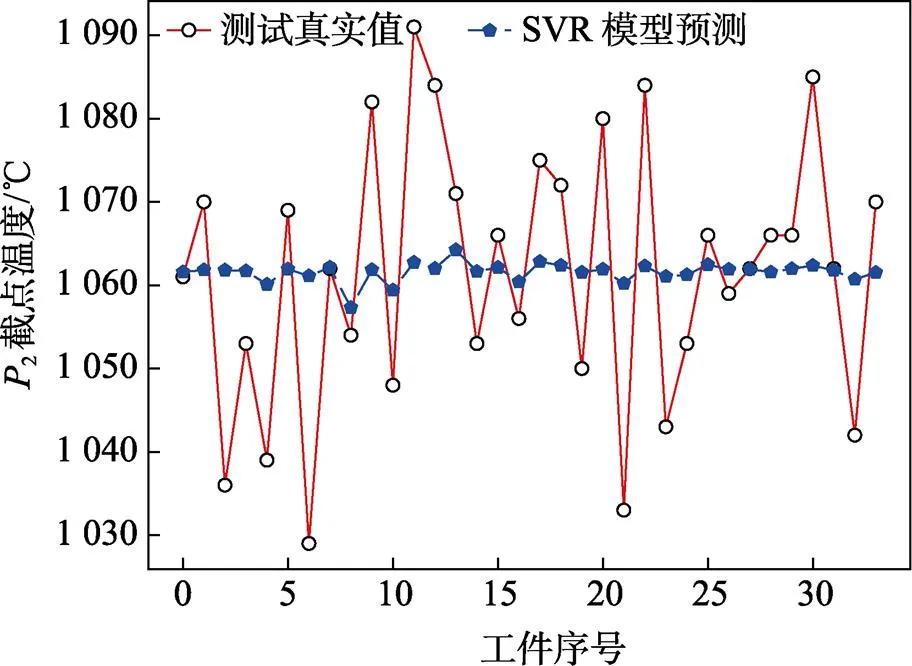
圖4 測試集SVR預測模型預測溫度折線圖

由圖3可知，學習曲線和驗證曲線基本保持一致，說明該模型的泛化能力較強，沒有出現過擬合情況，但從圖4可以看出，測試數據集中的預測效果較差，這可能是因為SVR模型參數沒達到最優以及出料溫度系統誤差較大。

2.3.3 GS–PSO優化模型參數

為進一步提升葉片擠壓過程中出料溫度預測模型的效果，文中利用GS–PSO算法對模型中的參數和進行優化，其中PSO初始參數取值如下：∈(1,210)，∈(2?10,26)，粒子群數量取30，粒子速率系數=0.6，學習因子1=2=2，慣性權重=0.6。再引入網格搜索（GS）計算其自適應度，對模型的參數進行優化，GS–PSO優化SVR模型三維粒子圖和自適應度的變化曲線如圖5和圖6所示。

圖5展示了粒子尋找最優參數的過程。由圖6可知，自適應度由大于0.007 8降到0.005 2左右，模型收斂快且優化效果顯著，30顆粒子迭代50次的最終優化結果為：=425.432 8，=1.883 2。

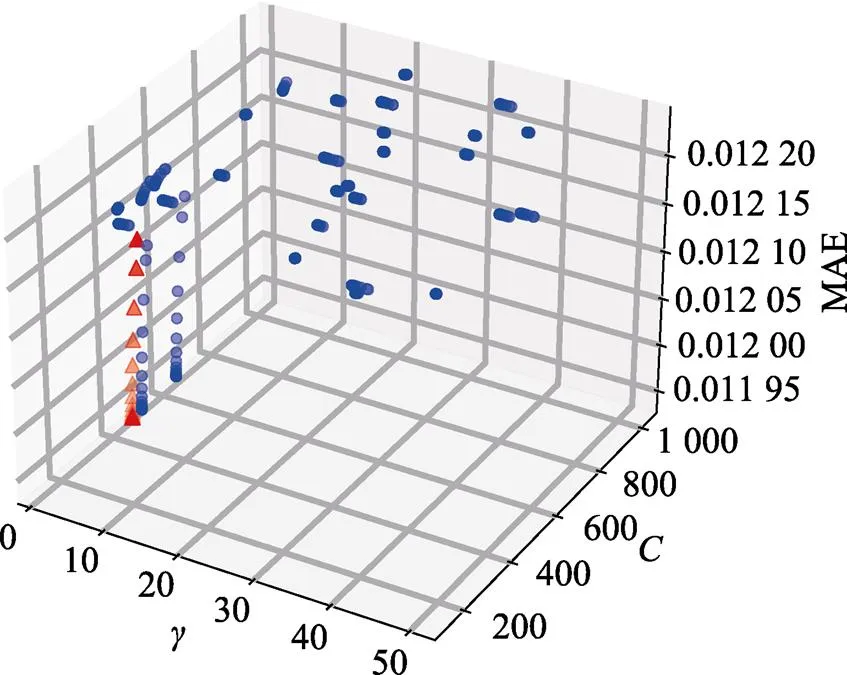
圖5 GS–PSO優化SVR模型三維粒子圖

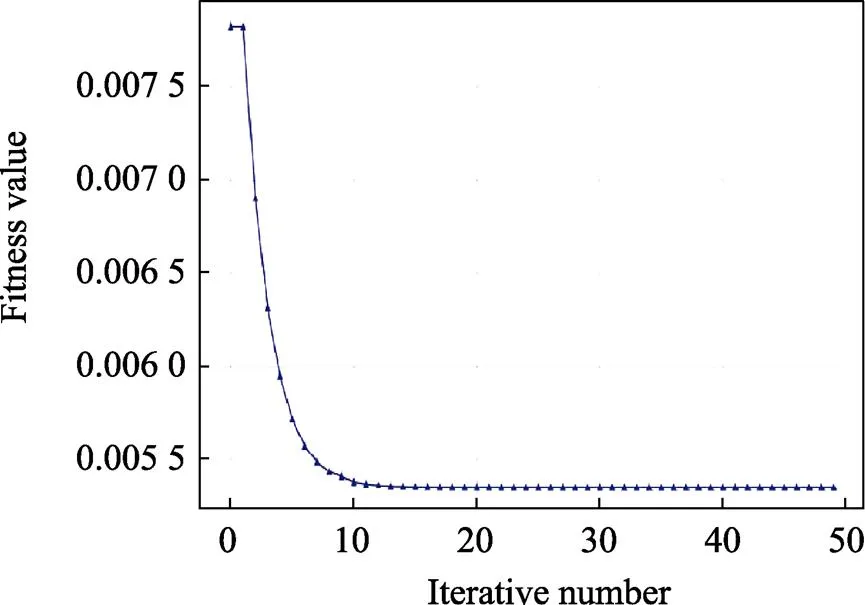
圖6 GS–PSO優化SVR模型自適應度曲線

3 預測結果及分析

在經過數據預處理、特征工程、參數優化和訓練集學習后，構建了GH4169轉子葉片精鍛擠壓過程出料溫度SVR預測模型，其在測試集中的預測結果如圖7所示。

圖7 P2點溫度測試集SVR預測折線圖（C=425.432 8，γ=1.883 2）

由圖7可知，模型優化后的預測精度有了很大提升，每組數據的預測誤差都遠小于10%，符合工業數據預測要求的一般標準，同時可以根據預測結果改進生產工藝，使出料溫度處于穩定的水平以控制葉片的晶粒質量指標。

4 結論

1）針對GH4169轉子葉片精鍛過程，利用GH4169轉子葉片精鍛的擠壓過程模擬數據集，建立了一種基于支持向量機并結合網格搜索及粒子群優化算法的回歸預測模型，對葉片擠壓的出料溫度進行分析預測。預測結果表明，預測值與實際值相近，該方法可為葉片精鍛質量控制提供決策信息，為降低葉片生產廢品率提供指導意義。

2）與單獨使用PSO和GS算法優化的模型相比，用GS–PSO算法優化后的GH4169轉子葉片精鍛的擠壓出料溫度SVR預測模型收斂更快、效果更好，該方法為材料加工精鍛過程質量回歸預測模型的優化提供了一種新途徑。

3）提出了基于支持向量回歸的葉片擠壓出料溫度預測方法，通過預測模型基于輸入量（工藝參數和模具參數）對輸出量（葉片溫度）進行預測，該方法不要求使用者具備相關專業知識，就可以提前自動診斷和預測零件加工過程的質量，具有通用性，對復雜生產過程的質量預測有一定的實用意義。

[1] 鐘杰, 胡楚江, 郭成. 葉片精密鍛造技術的發展現狀及其展望[J]. 鍛壓技術, 2008, 33(1): 1-5.

ZHONG Jie, HU Chu-jiang, GUO Cheng. Development Status and Prospects of Blade Precision Forging Technology[J]. Forging & Stamping Technology, 2008, 33(1): 1-5.

[2] ALLAM Z, BECKER E, BAUDOUIN C, et al. Forging Process Control: Influence of Key Parameters Variation on Product Specifications Deviations[J]. Procedia Engineering, 2014, 81(C): 2524-2529.

[3] 呂志民, 徐鋼, 毛文赫, 等. 冶金全流程工藝質量在線監控和離線分析診斷系統[J]. 冶金自動化, 2015, 39(3): 15-21.

LYU Zhi-min, XU Gang, MAO Wen-he, et al. Online Monitoring and Offline Analysis System for Products' Process Parameters and Quality of Whole Metallurgical Process[J]. Metallurgical Industry Automation, 2015, 39(3): 15-21.

[4] MILO M W, ROAN M, HARRIS B. A New Statistical Approach to Automated Quality Control in Manufacturing Processes[J]. Journal of Manufacturing Systems, 2015, 36: 159-167.

[5] ALLAM Z, BECKER E, BAUDOUIN C, et al. A Generic Methodology to Improve the Control of Forging Process Parameters[J]. Key Engineering Materials, 2013, 2443(554/555/556/557): 2138-2144.

[6] HAWRYLUK M, KASZUBA M, GRONOSTAJSKI Z. Systems of Supervision and Analysis of Industrial Forging Processes[J]. Eksploatacja i Niezawodnosc, 2016, 18(3): 315-324.

[7] 酆亞楠, 孫勇, 蘇暢, 等. 離散鍛造企業數據采集系統的實施與應用[J]. 鍛壓技術, 2018, 43(5): 162-166.

FENG Ya-nan, SUN Yong, SU Chang, et al. Implementation and Application of Data Collection System for Discrete Forging Company[J]. Forging & Stamping Technology, 2018, 43(5): 162-166.

[8] 曾琦. 曲軸智能鍛造系統及鍛件質量控制研究[D]. 北京: 北京科技大學, 2018: 22-107.

ZENG Qi. Study on Intelligent Forging System and Quality Control of Crankshaft[D]. Beijing: University of Science and Technology Beijing, 2018: 22-107.

[9] VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995: 374-395.

[10] 顧亞祥, 丁世飛. 支持向量機研究進展[J]. 計算機科學, 2011, 38(2): 14-17.

GU Ya-xiang, DING Shi-fei. Advances of Support Vector Machines(SVM)[J]. Computer Science, 2011, 38(2): 14-17.

[11] 丁世飛, 齊丙娟, 譚紅艷. 支持向量機理論與算法研究綜述[J]. 電子科技大學學報, 2011, 40(1): 2-10.

DING Shi-fei, QI Bing-juan, TAN Hong-yan. An Overview on Theory and Algorithm of Support Vector Machines[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 2-10.

[12] 尹浩霖, 王達夢, 馬志勇, 等. 支持向量回歸參數估計在風電機組故障模式分析中的應用[J]. 機械科學與技術, 2018, 37(11): 1755-1761.

YIN Hao-lin, WANG Da-meng, MA Zhi-yong, et al. Application of Support Vector Regression Parameter Estimation to Fault Mode Analysis in Wind Turbines[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(11): 1755-1761.

[13] 黃俊, 劉小生. 基于GS-PSO-SVM模型的邊坡穩定性預測模型[J]. 中國礦業, 2020, 29(6): 87-91.

HUANG Jun, LIU Xiao-sheng. Slope Stability Prediction Model Based on GS-PSO-SVM Model[J]. China Mining Magazine, 2020, 29(6): 87-91.

[14] 王健康, 張海波, 黃向華, 等. 基于在線滾動LS-SVR的渦軸發動機混合預測控制[J]. 航空學報, 2012, 33(10): 1755-1764.

WANG Jian-kang, ZHANG Hai-bo, HUANG Xiang-hua, et al. Hybrid Predictive Control for Turbo-Shaft Engine Based on Online Sliding LS-SVR[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1755-1764.

[15] 劉建新, 楊慶玲. ABC算法優化SVR的磨損故障預測模型[J]. 裝備環境工程, 2017, 14(11): 98-102.

LIU Jian-xin, YANG Qing-ling. Wear Fault Prediction Model Based on SVR Optimized by ABC[J]. Equipment Environmental Engineering, 2017, 14(11): 98-102.

[16] 彭彬彬, 閆獻國, 杜娟. 基于BP和RBF神經網絡的表面質量預測研究[J]. 表面技術, 2020, 49(10): 324-328.

PENG Bin-bin, YAN Xian-guo, DU Juan. Surface Quality Prediction Based on BP and RBF Neural Networks Full Text Replacement[J]. Surface Technology, 2020, 49(10): 324-328.

[17] SALCEDO-SANZ S, ROJO-áLVAREZ J. Support Vector Machines in Engineering: An Overview[J]. Wires: Data Mining & Knowledge Discovery, 2014, 4(3): 234-267.

[18] 章順虎, 姜興睿, 尤鳳翔, 等. 融合工業大數據的熱軋厚板軋制力模型研究[J]. 精密成形工程, 2020, 12(2): 8-14.

ZHANG Shun-hu, JIANG Xing-rui, YOU Feng-xiang, et al. Investigation on the Model of Rolling Force by Integrating Industrial Big Data[J]. Journal of Netshape Forming Engineering, 2020, 12(2): 8-14.

[19] JIANG Guo, BIN Wang, XU He-zeng, et al. A Novel Method for Workpiece Deformation Prediction by Amending Initial Residual Stress Based on SVR-GA[J]. Advances in Manufacturing, 2021, 9(4): 483-495.

[20] BEHROOZ K, NEHDI M L, NGUYEN-THOI T, et al. Predicting Load Capacity of Shear Walls Using SVR-RSM Model[J]. Applied Soft Computing Journal, 2021, 112: 106-121.

[21] 賈依達爾·熱孜別克, 袁逸萍, 孫文磊, 等. 根據PCA-GA-Elman的風機齒輪箱軸承溫度預測[J]. 機械科學與技術, 2020, 39(11): 1671-1675.

REZIBIEKE·Jiayidaer, YUAN Yi-ping, SUN Wen-lei, et al. Temperature Prediction of Wind Turbine Gearbox Bearing Based on PCA-GA-Elman[J]. Mechanical Science and Technology for Aerospace Engineering, 2020, 39(11): 1671-1675.

[22] 楊舜, 李宏, 劉印剛, 等. 葉片精密鍛造過程數值模擬技術研究進展[J]. 精密成形工程, 2015, 7(6): 44-51.

YANG Shun, LI Hong, LIU Yin-gang, et al. A Review on the Numerical Simulation Technology of Aerofoil Blade Precision Forging Process[J]. Journal of Netshape Forming Engineering, 2015, 7(6): 44-51.

Prediction of Discharge Temperature for Blade Extrusion Based on Support Vector Regression

DAI Nan1, YU Xin-hong1, GUO Jia-xin1, YU Qi-yan2

(1. School of Materials, Northwestern Polytechnical University, Xi'an 710072, China; 2. Xi'an Xiangxun Technology Limited Liability Company, Xi'an 710068, China)

The work aims to propose a way to predict the quality of traditional blade precision forging, so as to solve the large quality fluctuation of traditional blade precision forging. With the extrusion process of GH4169 rotor blade precision forging as the research object, 160 groups of simulation results of the precision forging extrusion process of blade were used as data sets, in which 120 groups of data were used as training sets, and the remaining 40 groups of data were used as test sets to predict the discharge temperature of the section point. First, specific data preprocessing methods and characteristics of the engineering model prediction accuracy and generalization ability were used to establish the SVR forecasting model. Then, based on grid search algorithm and particle swarm optimization algorithm (PSO), the forecast model parameterandwere adjusted to obtain the optimized model. At last, the test data was set into the optimized model. The predicted value was compared with the true value. The prediction effect of single SVR model was not good. After optimization with GS-PSO algorithm, the self-fitness of the model decreased from about 0.007 8 to about 0.005 2, with fast convergence and significant optimization effect. The final optimization result of 50 iterations for 30 particles was=425.432 8,=1.883 2. The fitted degree between the optimized predicted values and the actual values is good, and the prediction error of each group of data is much less than 10%. The prediction results show that the SVR prediction model optimized by GS-PSO has a good prediction effect in the test set, which meets the general standard requirements of industry data prediction, and has a good reference significance for the prediction of traditional blade precision forging process indexes.

blade precision forging; extrusion; data mining (DM); quality prediction

10.3969/j.issn.1674-6457.2022.08.002

TG315.9

A

1674-6457(2022)08-0013-07

2021–09–29

戴南（1998—），男，碩士生，主要研究方向為材料加工質量預測。

余心宏（1965—），男，碩士，教授，主要研究方向為材料加工現代設計理論與智能控制一體化技術。

責任編輯：蔣紅晨