誤差齒面下直齒輪副內部激勵及動態特性分析

劉 昶，石萬凱，劉 坤，劉 浩

(重慶大學 機械傳動國家重點實驗室，重慶 400044)

近年來隨著電動汽車的普及，對齒輪傳動系統振動噪聲性能要求明顯提高。齒輪傳動系統作為一種參數自激系統，即使不受外部激勵的影響，在內部激勵的作用下，系統也會產生自激振動[1]。時變嚙合剛度和綜合嚙合誤差是齒輪系統最重要的內部激勵[2]。因此，精確計算齒輪系統的時變嚙合剛度和綜合嚙合誤差，并在此基礎上研究各類型誤差對齒輪系統動態特性的影響規律，對預估和控制齒輪系統振動噪聲水平具有重要意義。

國內外學者已就齒距累積偏差[3]、齒廓偏差[4-5]、裂紋故障[6]、齒面微觀形貌[7]等對齒輪傳動系統動態特性的影響開展了廣泛研究。現有研究中，時變嚙合剛度的計算方法通常可分為有限元法和解析法兩大類[8]。有限元法因其計算結果精確而被廣泛接受和應用[9]。Yuan等[10]和Ma等[11]通過有限元方法分別研究了載荷和齒廓修形量對時變嚙合剛度的影響。隨著計算機技術的發展，盡管有限元法已在各個領域得到廣泛應用，但在計算齒輪時變嚙合剛度方面仍存在一些不足。一方面，有限元法的計算精度與網格質量有關，通常為了提高計算效率、降低計算成本，網格尺寸很難達到微米級，難以模擬齒輪加工誤差對時變嚙合剛度的影響；另一方面，為了簡化有限元模型，通常僅考慮齒輪副中的部分齒對，而每個輪齒的加工誤差不同，忽略了輪齒嚙合次序對時變嚙合剛度的影響。

相較于有限元法，解析法具有更高的計算效率，且其計算結果與有限元法計算結果一致性較好，因此近年來受到越來越多的關注。解析法中常用的有材料力學方法[12]和彈性力學方法[13]，但它們主要用于單齒剛度及單齒嚙合剛度的計算問題，而多齒嚙合時，常通過將單齒嚙合剛度簡單疊加得到。此外，在動力學分析時，多以理想齒輪為對象，計算其時變嚙合剛度，忽略了齒輪實際嚙合過程中，由加工、安裝誤差導致的輪齒脫嚙、線外接觸和偏載等一系列非正常嚙合現象對時變嚙合剛度的影響。

在齒輪動力學分析時，許多學者[14-16]采用簡諧函數模擬齒輪綜合嚙合誤差，且其幅值通常采用假設的方式或根據齒輪精度等級對應的公差值確定。然而，不同類型齒輪誤差導致的綜合嚙合誤差波形和幅值差異較大。此外，齒輪綜合嚙合誤差與時變嚙合剛度二者深度耦合，僅用簡諧函數模擬齒輪綜合嚙合誤差而不考慮對時變嚙合剛度的影響，難以得到較為精確的動力學分析結果。

基于上述原因，本文首先建立了考慮齒輪加工、安裝誤差的誤差齒面模型，提出了適用于該誤差齒面模型的承載接觸分析算法，并對直齒輪副的時變嚙合剛度和綜合嚙合誤差進行了精確計算。在此基礎上，建立了直齒輪副彎扭耦合動力學模型，研究了不同類型誤差對齒輪傳動系統動態特性的影響規律。

1 誤差齒面模型

為建立誤差齒面模型，首先將直齒輪齒面離散，如圖1所示。漸開線齒輪左右齒面分別被離散為n1×n2個相同大小的單元，各離散單元被近似為具有不同曲率半徑的圓柱面。假設每個離散單元具有一個控制點，且該控制點位于離散單元的中心，并通過索引i和j定義控制點在齒面上的編號。

圖1 直齒輪離散齒面Fig.1 Discrete tooth surface of spur gear

圖2 齒輪加工誤差示意圖Fig.2 Schematic diagram of gear manufacturing errors

(1)

(2)

(3)

(4)

(5)

(6)

圖3為本文中齒輪安裝誤差的定義。AgBg和ApBp分別是從動輪和主動輪不考慮安裝誤差時的理論軸線位置。為了簡化模型，本文中從動輪和主動輪的安裝誤差被等效轉換到從動輪的軸線上。Ag2Bg2是考慮安裝誤差后從動輪新的軸線位置。安裝誤差通過四個參數表示，即Δx，Δy，φ和γ。不同的安裝誤差可通過上述四個參數的不同組合獲得。a是標準中心距。考慮安裝誤差后，第n個輪齒誤差齒面上離散單元控制點的坐標可通過式(7)計算得到

圖3 安裝誤差示意圖Fig.3 Schematic diagram of assembly errors

(7)

式中：M13=(1-sinγ)tanφ-sinφ；M23=-sinγ/cosφ；M33=sinγ-cosφ-1；M14=Δx+B[sinφ-(1-sinγ)tanφ]；M24=a+Δy+Bsinγ/cosφ;M34=B(cosφ+1-sinγ)。

2 齒輪承載接觸分析

傳統的齒輪承載接觸分析算法計算過程復雜且存在數值不穩定等缺點[18]。圖4展示了本文所建立誤差齒面模型中的部分齒面。由圖4可知，該誤差齒面由多個大小相等的離散單元組成，且由于加工、安裝誤差的影響，各離散單元與理論齒面之間的距離不等。此外，為考慮由齒輪加工、安裝誤差導致的輪齒脫嚙、線外接觸等一系列非正常嚙合現象對時變嚙合剛度和綜合嚙合誤差的影響，本文提出通過檢測齒面干涉狀態來判定輪齒是否參與接觸，其又可轉化為通過檢測誤差齒面上離散單元的干涉狀態來判定輪齒是否參與接觸。

圖4 誤差齒面示意圖Fig.4 Schematic diagram of error tooth surface

齒輪承載接觸分析通過一個迭代過程完成，如圖5所示。當齒輪誤差齒面模型建立后，對于從動輪的每一個輸出位置，將以一定步長旋轉主動輪，每次迭代過程中判定輪齒是否接觸并計算齒輪副所產生的力矩，根據計算結果結合二分法調節主動輪旋轉步長，直至齒輪副所產生力矩與負載平衡，最終輸出從動輪各位置處的時變嚙合剛度和綜合嚙合誤差。

圖5 承載接觸分析流程圖Fig.5 Flow chart of load tooth contact analysis

切片法已廣泛應用于斜齒輪副時變嚙合剛度的研究中[19-21]。傳統切片法將齒輪沿齒寬方向劃分為多個切片，而每個切片之間是相互獨立的，即忽略切片之間的相互影響[22]。當齒輪為不考慮誤差的理想齒面時，該方法能取得較為準確的計算結果。然而，當考慮齒輪加工、安裝誤差時，齒面上會出現瞬時接觸線不連續、偏載等非正常嚙合現象，傳統切片法將導致較大的計算誤差。因此，本文引入名義切片的概念。如圖1所示，本文中誤差齒面也可看作由n1個切片組成，而每個切片又由n2個離散單元組成。齒輪傳動過程中，輪齒在載荷作用下會產生受載變形，而輪齒變形可被分為全局變形，包括輪齒彎曲、剪切、軸向壓縮以及齒輪基礎變形；局部變形，即赫茲接觸變形[23]。如圖6(a)所示，初始位置下，由于齒輪加工、安裝誤差的影響，各切片之間存在間隙和隨著主動輪的轉動，各切片之間的間隙減小且部分切片參與接觸，但由于齒輪副產生的力矩不足以與負載平衡，主動輪將繼續轉動，直至齒輪副所產生力矩與負載平衡，假設力矩平衡時，各切片接觸狀態如圖6(b)所示。假設失去接觸的切片與相鄰接觸切片具有相同的全局變形，并且這些切片共同構建了一個新的名義切片在每個名義切片上，具有最大變形量的切片被視為該名義切片的接觸中心。

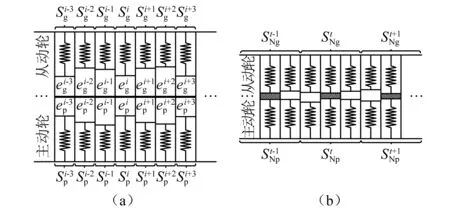
圖6 直齒輪副接觸過程Fig.6 Contact process of spur gear pair

(8)

(9)

根據Yang等[25]，大齒輪和小齒輪之間的赫茲接觸剛度可由式(10)計算

(10)

式中，E為齒輪材料彈性模量。

圖6(b)中各切片由多個離散單元組成，為通過式(8)計算各名義切片的嚙合剛度，還需確定各切片上參與嚙合單元的位置。前文中將各離散單元等效為具有不同曲率半徑的圓柱面，因此，兩齒輪齒面上任意兩個離散單元(Σngigjg和Σnpipjp)存在四種接觸狀態，如圖7所示。當不考慮安裝誤差時，兩離散單元(Σngigjg和Σnpipjp)的圓柱軸線平行，如圖7(a)和圖7(b)所示。基于空間直線方程，并結合離散單元控制點坐標和法向量可求得兩圓柱軸線之間的距離dc，則切片總變形為

(11)

式中，ρngigjg和ρnpipjp分別為離散單元Σngigjg和Σnpipjp對應的曲率半徑。

圖7 離散單元接觸狀態Fig.7 Contact state of two discrete elements

(12)

齒輪副力矩平衡方程為

(13)

齒輪副的時變嚙合剛度可通過所有名義切片的剛度求和而得

(14)

假設空載下主從動輪初始接觸時，從動輪的輸出位置為θg，而主動輪的轉動角度為θp，則綜合嚙合誤差為

e=(θg-θpzp/zg)rbg

(15)

式中，zg和zp分別為從動輪和主動輪齒數。

3 動力學建模

不考慮齒面摩擦的影響，建立如圖8所示直齒輪副彎扭耦合動力學模型。根據牛頓第二定律，可推得系統的動力學分析模型為

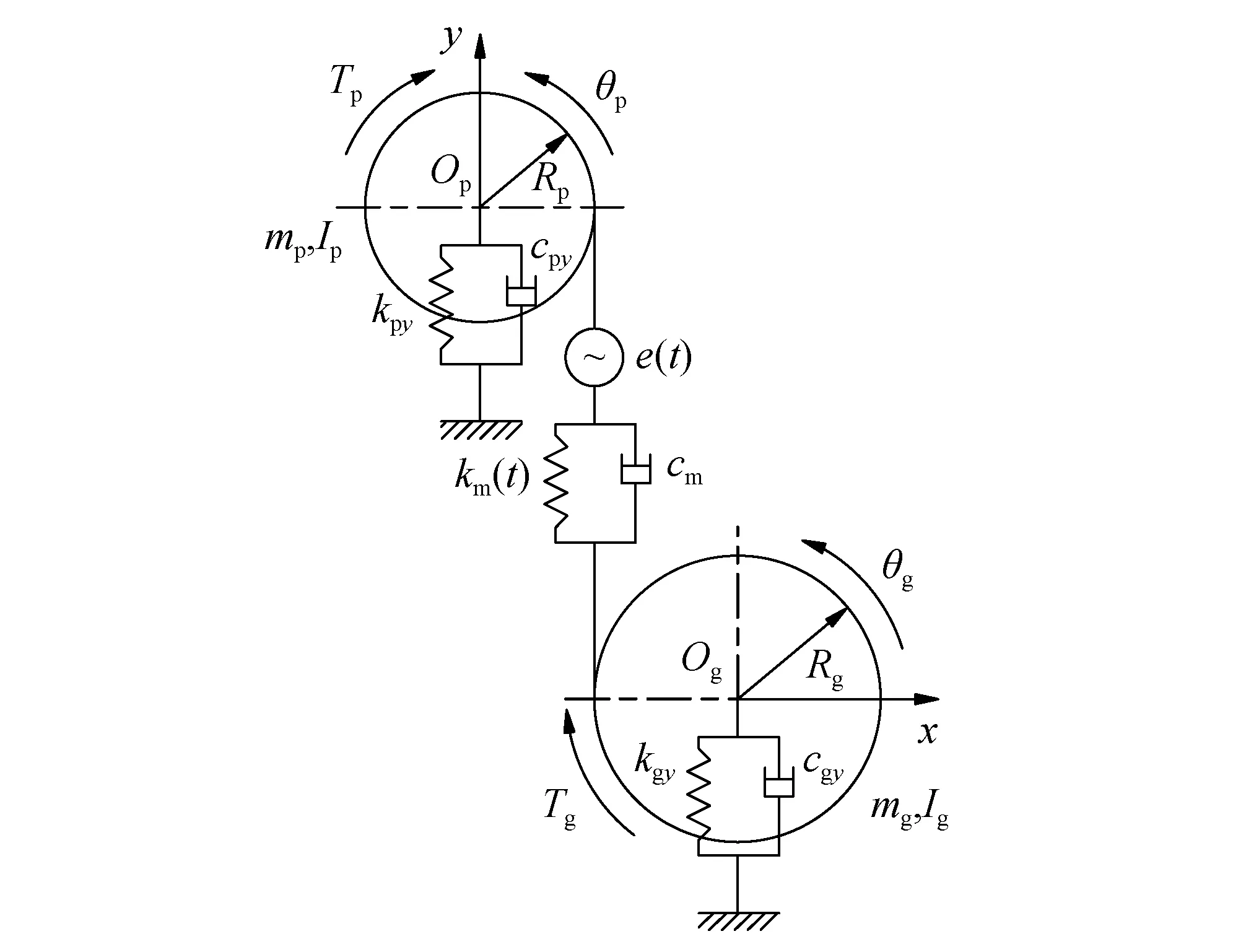
圖8 齒輪系統動力學模型Fig.8 Gear system dynamic model

(16)

式中，下標p和g分別為主動輪和從動輪；m和I分別為齒輪的質量和轉動慣量；ky和cy分別為齒輪沿y方向的支撐剛度和阻尼；y和θ分別為齒輪在y方向和扭轉方向的振動位移；rb為齒輪的基圓半徑；T為齒輪的扭矩；cm和km(t)分別為嚙合阻尼和時變嚙合剛度；δ為沿嚙合線的動態傳遞誤差，δ可表示為

δ=-yp-rbpθp+yg-rbgθg-e(t)

(17)

式中，e(t)為時變綜合嚙合誤差。

動力學方程中時變嚙合剛度和時變綜合嚙合誤差可分別通過式(14)和式(15)求得。本文中忽略嚙合阻尼的時變性，嚙合阻尼通過經驗公式求得，計算公式為[26]

(18)

式中：ξ為輪齒嚙合阻尼比，一般為0.03～0.17，本文取0.1；km為時變嚙合剛度均值。

4 計算結果分析與討論

4.1 模型驗證

為了驗證本文中齒面離散模型及承載接觸分析算法的計算精度，以Chen等研究中的齒輪副為對象，計算理論齒面下的時變嚙合剛度和綜合嚙合誤差。本文與Chen等研究中時變嚙合剛度計算結果對比如圖9所示。通過對比可知，時變嚙合剛度均值和峰峰值分別相差2.05%和0.90%，且時變嚙合剛度隨接觸齒對數目的變化而發生突變。此外，理論齒面下，整個嚙合周期內齒輪副綜合嚙合誤差為0。上述結果驗證了本文中齒面離散模型以及承載接觸分析算法的可行性，并說明該方法具有較高的計算精度。

圖9 時變嚙合剛度和接觸齒對數Fig.9 Time-varying meshing stiffness and number of contact tooth pairs

4.2 加工誤差對內部激勵影響分析

齒輪副時變嚙合剛度和綜合嚙合誤差的計算結果不僅受到加工和安裝誤差的影響，還會受到輪齒嚙合次序的影響。當主從動齒輪齒數不同時，主動輪旋轉一周后，相互嚙合的輪齒發生變化，從而影響時變嚙合剛度和綜合嚙合誤差的計算結果。為了避免計算周期過長，本文中選用具有相同齒數的主從動輪作為研究對象，齒輪副參數如表1所示。

表1 直齒輪副參數Tab.1 Parameters of spur gear pair

本文中主從動齒輪均采用5級精度，根據ISO齒輪精度標準，齒輪副精度參數如表2所示。

表2 直齒輪副精度參數Tab.2 Precision parameters of spur gear pair

齒距累積偏差通常在多個輪齒上大致呈正弦形式分布，多數文獻中使用正弦函數來模擬齒距累積偏差，但忽略了齒距累積偏差的隨機性。參照袁冰等研究中齒距累積偏差生成模式，本文中采用正弦函數與服從正態分布的隨機變量疊加來模擬齒距累積偏差。主動輪和從動輪的齒距累積偏差如圖10所示。另外，齒面各離散單元齒廓偏差幅值和各輪齒齒厚偏差幅值均通過隨機函數在其公差帶中選取。當齒輪生成完成后，校核其公法線長度，若不滿足要求，則上述偏差重新選取，直至齒輪副所有精度參數滿足表2中所示公差范圍。

圖10 齒距累積偏差Fig.10 Cumulative pitch deviation

不同類型加工誤差影響下直齒輪副時變嚙合剛度和綜合嚙合誤差，如圖11所示。由圖11可知，理論齒面下時變嚙合剛度呈周期性變化，且綜合嚙合誤差為0。當考慮齒距偏差時，時變嚙合剛度在θ1= 0.932 0 rad和θ=2.265 4 rad處發生突變，且在θ1區間[0.932 0,1.017 5]和[2.122 3,2.265 4]中時變嚙合剛度大幅減小。此外，當考慮齒距偏差時，綜合嚙合誤差發生階躍變化，這說明由于齒距偏差的影響，在嚙合齒面間產生了不同的初始間隙。為研究時變嚙合剛度產生突變及大幅減小的原因，計算了從動輪不同轉角下接觸齒對數目，如圖12(a)所示。在θ1區間[0.932 0,1.017 5]和[2.122 3,2.265 4]中，由于齒距偏差的影響，接觸齒對數目由雙齒接觸變為單齒接觸，從而導致時變嚙合剛度大幅減小，甚至發生突變。同時，結合圖11(b)中綜合嚙合誤差分析可知，綜合嚙合誤差階躍值最大為5.580 8 μm，其次為4.669 7 μm，它們分別對應區間[2.122 3,2.265 4]和[0.932 0,1.017 5]與相鄰區間綜合嚙合誤差的差值。由此說明，齒距偏差導致嚙合齒面間產生初始間隙，而該間隙無法被輪齒受載變形補償時，將導致部分齒對脫嚙，也即當齒輪綜合嚙合誤差階躍值超過一定范圍后會導致時變嚙合剛度發生突變。

圖11 不同加工誤差下時變嚙合剛度和綜合嚙合誤差Fig.11 Time-varying meshing stiffness and composite meshing error considering different types of manufacturing errors

由圖11(a)可知，當考慮齒厚偏差時，時變嚙合剛度略微減小，且各嚙合周期中時變嚙合剛度減小值不同。圖12(b)為齒厚偏差影響下從動輪旋轉1.570 8 rad時主動輪齒面瞬時接觸線，雖然瞬時接觸線與理論接觸跡重合，但是考慮齒厚偏差會使輪齒減薄，單齒柔度增加，從而使時變嚙合剛度略微減小。此外，由圖11(b)可知，當考慮齒厚偏差時，綜合嚙合誤差為0。這是由于本文中齒厚偏差通過輪齒的右側齒面定義，齒距偏差通過左側齒面定義，如圖2所示，而本研究中左側齒面為工作齒面，因此齒厚偏差的引入并不影響齒輪副的綜合嚙合誤差。

當考慮齒廓偏差時，時變嚙合剛度和綜合嚙合誤差在其理論值附近產生微小波動。圖12(c)為齒廓偏差影響下從動輪旋轉1.570 8 rad時主動輪齒面瞬時接觸線。由圖可知，受齒廓偏差的影響，主動輪齒面接觸線不再與理論接觸跡重合，而是分布在其兩側，即發生了線外接觸，這是時變嚙合剛度和綜合嚙合誤差產生微小波動的原因。

圖12 不同加工誤差下齒面瞬時接觸狀態Fig.12 Instantaneous contact state of tooth surface considering different types of manufacturing errors

由上述分析可知，齒距偏差是影響時變嚙合剛度和綜合嚙合誤差的主要因素。此外，加工誤差的引入會同時影響時變嚙合剛度和綜合嚙合誤差，二者深度耦合。在動力學分析過程中，僅通過簡諧函數模擬綜合嚙合誤差，而忽略加工誤差對時變嚙合剛度的影響，難以得到較為精確的動力學分析結果。

4.3 安裝誤差對內部激勵影響分析

根據圖3中對安裝誤差的定義，安裝誤差由四個參數(Δx，Δy，φ和γ)表示，它們可被分為中心距誤差(Δx和Δy)和軸線傾斜誤差(φ和γ)兩類。由于Δx和Δy對齒輪副中心距的變化影響類似，因此本文中僅考慮安裝誤差Δy，φ和γ對時變嚙合剛度和綜合嚙合誤差的影響，安裝誤差參數如表3所示。

表3 直齒輪副安裝誤差Tab.3 Assembly errors of spur gear pair

不同安裝誤差下時變嚙合剛度和綜合嚙合誤差，如圖13所示。由圖13(a)可知，在安裝誤差Δy的影響下，當中心距增大時，時變嚙合剛度減小，且由于中心距增大，嚙合齒面間初始間隙增加，從而導致單齒嚙合區間變大，而雙齒嚙合區間變小；當中心距減小時，時變嚙合剛度增加，而對單、雙齒嚙合區間影響較小，甚至出現單齒嚙合區間略微變大，這是由于在本文28 N·m載荷和-0.2 mm中心距誤差下，時變嚙合剛度增加導致輪齒受載變形減小，反而延緩了第二對輪齒進入嚙合。此外，在安裝誤差φ和γ的影響下，時變嚙合剛度具有不同程度的減小，而單、雙齒嚙合區間無明顯變化，且針對相同大小的軸線傾斜誤差(φ和γ)，軸線傾斜誤差φ對時變嚙合剛度的影響更大。圖14為從動輪旋轉0.314 2 rad時，主動輪齒面瞬時接觸線。由圖14(a)和圖14(d)可知，由于中心距誤差Δy的引入，當中心距增加時，主動輪齒面瞬時接觸線向齒頂移動，從而導致時變嚙合剛度減小；相反地，當中心距減小時，主動輪齒面接觸線向齒根移動，從而使時變嚙合剛度增加。由圖14(b)、圖14(c)、圖14(e)和圖14(f)可知，在軸線傾斜誤差φ和γ的影響下，主動輪齒面發生了不同程度的偏載，齒面實際接觸線縮短，從而導致時變嚙合剛度減小。當φ=±0.1°時，約50%的齒面脫離接觸，而當γ=±0.1°時，約33%的齒面脫離接觸，因此相同大小誤差下，軸線傾斜誤差φ對時變嚙合剛度的影響大于軸線傾斜誤差γ。

圖13 不同安裝誤差下時變嚙合剛度和綜合嚙合誤差Fig.13 Time-varying meshing stiffness and composite meshing error considering different types of assembly errors

由圖13(b)可知，在安裝誤差的影響下，齒輪副綜合嚙合誤差為一定值，且當齒面為理論齒面或軸線傾斜誤差φ=-0.1°和γ=0.1°時，綜合嚙合誤差為0。當φ=0.1°和γ=-0.1°時，綜合嚙合誤差分別為32.884 5 μm和11.928 0 μm。當中心距減小時(Δy=-0.2 mm)，綜合嚙合誤差為正值，即67.394 3μm；當中心距增大時(Δy=0.2 mm)，綜合嚙合誤差為負值，即-69.392 3 μm。

4.4 系統動態特性分析

為研究加工誤差和安裝誤差對系統動態特性的影響，將上文求得的時變嚙合剛度和綜合嚙合誤差代入動力學方程，并在MATLAB軟件中利用ODE15S進行仿真，計算了不同誤差下齒輪副的動態傳遞誤差，并對計算結果在時域和頻域內進行分析。

理論齒面下和所有類型加工誤差綜合作用下齒輪副動態傳遞誤差及其頻譜特性，如圖15所示。本研究中主動輪轉速為2 400 r/min，嚙合頻率為fm=0.1×104Hz。由圖15可知，理論齒面下動態傳遞誤差峰峰值為4.158 2 μm，其頻譜成分主要為嚙合頻率及其倍頻。考慮所有類型加工誤差時，動態傳遞誤差峰峰值為7.437 4 μm，其峰峰值較理論齒面明顯增大。此外，對比圖15(c)和圖15(d)可知，考慮所有類型加工誤差后，動態傳遞誤差頻譜中1×104～2×104Hz間高頻成分顯著增加，而幅值有所減小。為研究動態傳遞誤差的主要影響因素及頻譜中高頻成分的來源，分別對不同類型加工誤差作用下的動態傳遞誤差進行了分析，如圖16所示。

當分別考慮齒距偏差、齒厚偏差和齒廓偏差時，動態傳遞誤差峰峰值分別為8.392 1 μm，4.043 5 μm和5.396 1 μm。與理論齒面下動態傳遞誤差計算結果對比可知，齒距偏差和齒廓偏差均導致動態傳遞誤差峰峰值增加，且齒距偏差的影響大于齒廓偏差，而齒厚偏差對動態傳遞誤差峰峰值的影響較小。雖然當僅考慮齒厚偏差時和理論齒面下，綜合嚙合誤差均為0，但齒厚偏差的引入導致輪齒減薄，時變嚙合剛度的變化導致動態傳遞誤差峰峰值減小。相較于齒廓偏差，當考慮齒距偏差時，動態傳遞誤差峰峰值與考慮所有類型加工誤差時動態傳遞誤差的峰峰值更為接近。此外，從動態傳遞誤差的頻譜分析圖可以看出，當僅考慮齒厚偏差時，其頻譜成分與理論齒面下相同，均為嚙合頻率及其倍頻，而當考慮齒距偏差和齒廓偏差時，動態傳遞誤差頻譜中1×104～2×104Hz間高頻成分均有增加，其中齒距偏差下動態傳遞誤差高頻成分增加更為顯著，且與考慮所有類型加工誤差時的頻譜成分更為接近。因此，齒距偏差是影響動態傳遞誤差的主要因素，且齒距偏差是動態傳遞誤差頻譜中高頻成分的主要來源。為減小齒輪系統動態傳遞誤差的峰峰值，齒距偏差應根據載荷大小合理分配，避免由于輪齒脫嚙導致的時變嚙合剛度突變對動態傳遞誤差的影響。

圖17為不同安裝誤差下動態傳遞誤差計算結果。根據前文中時變嚙合剛度和綜合嚙合誤差計算結果可知，理論齒面下和軸線傾斜誤差φ=-0.1°以及γ=0.1°時，綜合嚙合誤差均為0，通過對比圖15(a)、圖17(c)和圖17(e)可見，時變嚙合剛度均值越小，動態傳遞誤差均值越大。此外，圖17(a)～圖17(f)中，動態傳遞誤差的峰峰值分別為6.002 8 μm，4.675 9 μm，2.899 4 μm，4.717 0 μm，5.033 0 μm和2.882 0 μm。由圖13和圖14可知，當γ=0.1°時，約33%的齒面脫離接觸，時變嚙合剛度均值和峰峰值減小，從而導致動態傳遞誤差的峰峰值減小；然而，當φ=-0.1°時，約50%齒面脫離接觸，時變嚙合剛度的均值和峰峰值進一步減小，反而使動態傳遞誤差的峰峰值增加。對中心距誤差而言，當Δy為負偏差時，時變嚙合剛度均值增加；當Δy為正偏差時，時變嚙合剛度均值減小；同樣大小的中心距誤差下，負偏差對動態傳遞誤差峰峰值的影響小于正偏差。由圖13(b)可知，在安裝誤差影響下，齒輪副綜合嚙合誤差為一定值。對比圖17(b)和圖17(e)可知，當時變嚙合剛度相同時，綜合嚙合誤差的均值對動態傳遞誤差的均值和峰峰值影響較小。此外，從動態傳遞誤差的頻譜分析中可以看出，不同類型安裝誤差下，其頻譜成分主要為嚙合頻率及其倍頻。

圖17 不同類型安裝誤差對動態傳遞誤差的影響Fig.17 Influence of different types of assembly errors on dynamic transmission error

綜上分析可知，為減小動態傳遞誤差的峰峰值，應避免由軸線傾斜誤差引起的偏載現象發生，雖然一定程度內的偏載導致時變嚙合剛度均值和峰峰值減小，使動態傳遞誤差峰峰值減小，但超過一定范圍后，不僅動態傳遞誤差的峰峰值增加，也會導致齒面接觸應力增加，縮短齒輪疲勞壽命。此外，雖然本文中中心距負偏差對動態傳遞誤差峰峰值的影響小于正偏差，但是中心距負偏差會進一步導致嚙入沖擊激勵增大，不利于改善高速齒輪系統的動態性能。

5 結 論

(1)加工、安裝誤差同時影響時變嚙合剛度和綜合嚙合誤差，二者深度耦合。加工誤差中，齒距偏差是時變嚙合剛度和綜合嚙合誤差的主要影響因素；齒距偏差作用下，綜合嚙合誤差呈階躍變化，當階躍值超過一定范圍后會導致輪齒脫嚙，時變嚙合剛度發生突變；齒距偏差也是齒輪系統動態傳遞誤差的主要影響因素。

(2)安裝誤差影響下，綜合嚙合誤差在整個嚙合周期內為一定值；中心距誤差導致瞬時接觸線在齒面上移動，時變嚙合剛度隨中心距的增加而減小；軸線傾斜誤差導致齒輪出現偏載現象，齒面接觸線縮短，時變嚙合剛度減小，且軸線傾斜誤差φ較軸線傾斜誤差γ對時變嚙合剛度的影響更大。

(3)為減小齒輪系統動態傳遞誤差的峰峰值，齒距偏差應根據載荷大小合理分配，同時應避免由軸線傾斜誤差引起的偏載現象發生；此外，雖然中心距負偏差對動態傳遞誤差峰峰值的影響小于正偏差，但在采用中心距負偏差時，應結合齒廓修形，降低由中心距負偏差帶來的嚙入沖擊。