基于聲學(xué)虹吸效應(yīng)的水下低頻大寬帶吸聲機(jī)理研究

馬承志，王立博，吳 曉，吳九匯

(1.西安交通大學(xué) 機(jī)械工程學(xué)院，西安 710049；2.西安交通大學(xué) 機(jī)械結(jié)構(gòu)強(qiáng)度與振動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室，西安 710049)

近年來(lái)，聲學(xué)超材料因其對(duì)低頻聲的良好吸聲性能而得到迅速發(fā)展。與傳統(tǒng)材料相比[1-5]，如多孔材料、穿孔或微穿孔板，超材料能夠?qū)崿F(xiàn)以更小的結(jié)構(gòu)尺寸達(dá)到更高的能量耗散效率。到目前為止，已經(jīng)獲得了一系列新的超材料，其中大部分能夠以亞波長(zhǎng)厚度實(shí)現(xiàn)聲音近乎100%的吸聲，包括膜型超材料[6-11]，聲學(xué)超材料[12-18]，纏繞空間超材料[19-22]，慢波超材料[23-26]，亥姆霍茲諧振器[27-28]。目前，空氣聲吸聲材料已經(jīng)逐步趨于成熟，水下吸聲材料也有不錯(cuò)的研究進(jìn)展[29-40]，但水下全頻段的吸聲尤其是低頻段仍需進(jìn)一步研究突破。因此，實(shí)現(xiàn)水下低頻高效吸聲成為當(dāng)前的研究熱點(diǎn)和科學(xué)挑戰(zhàn)之一。

在前人工作和研究的基礎(chǔ)上，我們提出了一種水下薄板型超材料，該超材料具有多個(gè)元胞可以具有多個(gè)低頻吸聲峰。在該多元胞結(jié)構(gòu)作用下其同一位置處共振峰值頻率較單個(gè)元胞結(jié)構(gòu)略微變化，但吸聲性能仍能保持較高的水平。更具體地說(shuō)，在壓差聲匯機(jī)理作用下，整個(gè)入射聲能被迫從周?chē)飨蚰骋辉瑥亩岣吡嗽恼駝?dòng)強(qiáng)度，振動(dòng)幅值大大提高，進(jìn)而將聲能轉(zhuǎn)化為彈性應(yīng)變能在結(jié)構(gòu)阻尼的作用下實(shí)現(xiàn)了能量的耗散，表現(xiàn)出良好的吸聲效果。在聲學(xué)虹吸效應(yīng)作用下單個(gè)元胞的自振特性基本沒(méi)有改變，因此峰值頻率大體上保持不變或略微變化。此外，通過(guò)深入研究該效應(yīng)作用下的吸聲機(jī)理及其對(duì)吸聲性能的影響，本文正式提出基于聲學(xué)虹吸效應(yīng)的低頻大寬帶吸聲機(jī)理，為超材料設(shè)計(jì)提供更好的物理解釋。

論文結(jié)構(gòu)如下:第一部分，介紹了基于聲學(xué)虹吸效應(yīng)的低頻大寬帶吸聲機(jī)理的薄板型超材料；第二部分，通過(guò)壓差聲匯機(jī)理、聲阻抗匹配機(jī)理及等效負(fù)動(dòng)態(tài)質(zhì)量密度機(jī)理驗(yàn)證了該薄板型超材料的低頻大寬帶吸聲性能；第三部分，詳細(xì)研究了面積比及主要參數(shù)對(duì)薄板型超材料吸聲性能的影響；第四部分，對(duì)薄板型超材料的各項(xiàng)參數(shù)進(jìn)行合理設(shè)計(jì)優(yōu)化，實(shí)現(xiàn)了水下100～500 Hz的低頻大寬帶吸聲效果；第五部分，進(jìn)行了總結(jié)。

1 薄板型超材料有限元模型

1.1 模型建立情況

為了說(shuō)明低頻大寬帶吸聲機(jī)理，給出了兩種模型，單元胞結(jié)構(gòu)(元胞一)如圖1(a)所示和元胞一元胞二組合的雙元胞結(jié)構(gòu)如圖1(b)所示，元胞二是通過(guò)改變?cè)坏膮?shù)而得到的新元胞。該單元胞結(jié)構(gòu)由三部分組成:一塊矩形的薄板，薄板由復(fù)合鋼板[41-46]構(gòu)成，兩個(gè)相同的半圓形鉛塊和一個(gè)聲學(xué)剛性框架。計(jì)算中使用的材料參數(shù)如表1所示。元胞一是將兩個(gè)直徑d1=104 mm、高度均為h1=37.5 mm、間距D1=104 mm的半圓塊分別對(duì)稱(chēng)固定在薄板上，薄板的寬度W=150 mm、長(zhǎng)度L=300 mm、厚度S=1.2 mm。薄板的邊界固定在聲學(xué)剛性框架上，該框架為上下貫通的通腔，壁厚t=3 mm。元胞二是在元胞一的基礎(chǔ)上對(duì)部分參數(shù)進(jìn)行了調(diào)整，半圓塊直徑d2=110 mm、高度h2=105 mm、間距D2=110 mm，其他參數(shù)均與元胞一相同。

表1 計(jì)算所用到的材料參數(shù)Tab.1 Calculate the material parameters used

圖1 仿真模型Fig.1 Simulation structure

為了獲得該超材料的吸聲性能，利用商用有限元軟件COMSOL MultiphysicsTM 5.6建立了聲-固耦合的有限元仿真模型。薄板、質(zhì)量塊被定義為固體域，其余部分被定義為聲學(xué)域；沿z軸負(fù)方向，將平面入射波P=10 Pa垂直地施加于該超材料表面；邊界條件設(shè)置為固定約束，該約束施加在每個(gè)元胞薄板的外邊緣；材料參數(shù)和幾何尺寸與上述參數(shù)保持一致。此外，水的密度和水中的聲速分別為ρ0=1 000 kg/m3和c0=1 500 m/s。

根據(jù)能量守恒定理，入射聲波Ii的能量轉(zhuǎn)化為以下三部分組成：反射聲波Ir的能量、透射聲波It的能量以及聲能轉(zhuǎn)化為結(jié)構(gòu)共振后所耗散的能量Iα。因此，該超材料所耗散的能量Iα可以表示為

Iα=Ii-Ir-It

(1)

聲強(qiáng)吸聲系數(shù)α定義為Iα和Ii的比值

(2)

式中：RI為聲強(qiáng)反射系數(shù)；TI為聲強(qiáng)透射系數(shù)[47]。

在不考慮聲波傳播過(guò)程中媒質(zhì)損耗問(wèn)題情況下，薄板質(zhì)量塊吸聲結(jié)構(gòu)其吸聲系數(shù)α≤50%[48]

(3)

式中，pia和pta分別為入射聲波和透射聲波的聲壓幅值。

1.2 共振模態(tài)分析

薄板型超材料的吸聲是聲能轉(zhuǎn)化為彈性應(yīng)變能在結(jié)構(gòu)阻尼作用下來(lái)實(shí)現(xiàn)能量耗散的結(jié)果，共振時(shí)，可以實(shí)現(xiàn)最大的能量耗散。圖2給出了單元胞結(jié)構(gòu)(元胞一、元胞二)及雙元胞結(jié)構(gòu)的吸聲系數(shù)及共振模態(tài)。通過(guò)對(duì)比可以看出，在雙元胞結(jié)構(gòu)下元胞一具有一個(gè)吸聲峰，對(duì)應(yīng)451 Hz處的共振模態(tài):半圓質(zhì)量塊直邊的平移、扭轉(zhuǎn)運(yùn)動(dòng)加上薄板中心的劇烈振動(dòng)；元胞二具有兩個(gè)吸聲峰，分別對(duì)應(yīng)143 Hz和312 Hz處共振模態(tài)，從而使得雙元胞結(jié)構(gòu)獲得了三個(gè)吸聲峰。值得注意的是，與單元胞結(jié)構(gòu)的吸聲峰相比較，雙元胞結(jié)構(gòu)在對(duì)應(yīng)頻率處的振動(dòng)模態(tài)基本上不發(fā)生改變，質(zhì)量塊的主要振型不會(huì)發(fā)生大的改變，但振動(dòng)幅值增加，吸聲峰值頻率略微改變，仍然具有很好的吸聲效果。在第一個(gè)吸聲峰和第二個(gè)吸聲峰之間有一個(gè)比較小的峰值，主要是因?yàn)楫?dāng)該頻率的聲波入射到雙元胞結(jié)構(gòu)表面時(shí)，該雙元胞結(jié)構(gòu)在此頻率處產(chǎn)生了一個(gè)新的微小的共振，該共振與其他頻率處的強(qiáng)烈共振相比較較為微弱，該結(jié)構(gòu)主要是通過(guò)結(jié)構(gòu)共振在結(jié)構(gòu)阻尼的作用下耗散能量進(jìn)行吸聲，所以達(dá)不到很好的吸聲效果，出現(xiàn)了一個(gè)比較小的峰值。

圖3(a)和圖3(b)顯示了聲能量流在吸聲頻率為451 Hz時(shí)雙元胞結(jié)構(gòu)中的分布，從圖中可以看出，在元胞一和元胞二之間的表面壓差作用下，使得大部分入射能量從周?chē)鷧^(qū)域流向元胞一。如圖2(b)和圖2(g)所示，元胞一的振動(dòng)幅值從47×10-6mm 提高到8×10-5mm，與單元胞結(jié)構(gòu)(元胞一)相比，雙元胞結(jié)構(gòu)的聲學(xué)虹吸效應(yīng)增強(qiáng)了單元胞結(jié)構(gòu)(元胞一)質(zhì)量塊的振動(dòng)。特別是圖2(h)所示的總彈性應(yīng)變能，在共振頻率處，雙元胞結(jié)構(gòu)的總彈性應(yīng)變能約為單元胞結(jié)構(gòu)的兩倍多。所以當(dāng)吸聲面積是入射面積的一半時(shí)，雙元胞結(jié)構(gòu)仍然具有有較高的吸聲系數(shù)。總而言之，聲學(xué)虹吸效應(yīng)雖然增強(qiáng)了振動(dòng)，但主要共振元胞的固有振動(dòng)特性基本保持不變，并且其他元胞相較于共振元胞來(lái)說(shuō)，振動(dòng)振幅很小或基本保持不動(dòng)，使得整體結(jié)構(gòu)對(duì)應(yīng)的峰值頻率變化不大只是略微進(jìn)行了移動(dòng)，具有很好的吸聲效果。該研究表明在多元胞情況下，入射能量增大，在某一元胞的作用下將周?chē)穆暷芰砍槲^(guò)來(lái)，使得該元胞處的能量增強(qiáng)，進(jìn)而振動(dòng)的能量增強(qiáng)，質(zhì)量塊振動(dòng)的幅值增大，元胞結(jié)構(gòu)的彈性應(yīng)變能增大，從而將聲能轉(zhuǎn)化為彈性應(yīng)變能在結(jié)構(gòu)阻尼作用下進(jìn)行耗散，在面積變大的多元胞結(jié)構(gòu)中仍然具有很好的吸聲效果。在后面的章節(jié)中，將具體討論該超材料吸聲的物理機(jī)理，同時(shí)為了排除其他因素的干擾，更好地體現(xiàn)面積比對(duì)該薄板型超材料吸聲的影響，我們對(duì)不同面積比情況下單元胞的吸聲性能也進(jìn)行了相應(yīng)的研究。

圖2 結(jié)構(gòu)的吸聲及振動(dòng)情況Fig.2 Sound absorption and vibration of the structure

2 薄板型超材料吸聲的多重物理機(jī)理分析

2.1 壓差聲匯機(jī)理

本節(jié)以薄板型超材料的雙元胞結(jié)構(gòu)為例，通過(guò)理論分析來(lái)解釋壓差聲匯機(jī)理。

雙元胞結(jié)構(gòu)如圖1(b)所示，假設(shè)吸聲結(jié)構(gòu)由兩個(gè)元胞組成:元胞一和元胞二，其中兩元胞表面聲阻抗率分別為Zs1，Zs2。

(4)

當(dāng)平面波從z<0區(qū)域垂直作用于元胞表面時(shí)，入射聲壓場(chǎng)Pi和反射聲壓場(chǎng)Pr可表示為

(5)

式中：pia為入射聲壓振幅；ω為角頻率；k為波數(shù)；γ為反射聲壓幅值的放大系數(shù)；σπ為入射波和反射波之間的相位差。

因此，總聲壓場(chǎng)P為

P=piaexp(jωt)[exp(-jkz)+γexp(jkz+σπ)]

(6)

水中粒子速度為

(7)

式中，ρ0c0為水的特征阻抗。

由式(6)和式(7)可得結(jié)構(gòu)表面聲阻抗率，并由此獲得在z=0處的聲阻抗率

(8)

(9)

因?yàn)閆s=Rs+jXs,Rs和Xs分別為聲阻率、聲抗率，所以聲阻抗率比還可表示成

ξ=xs+jys

(10)

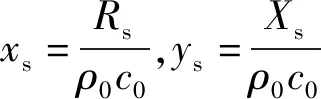
(11)

元胞一和元胞二的表面壓力表示為

(12)

最后，給出兩元胞之間的表面聲壓差Δp

Δp=piaexp(jωt)[γ2exp((σπ)2)-
γ1exp((σπ)1)]

(13)

正是阻抗不匹配引起的表面壓差導(dǎo)致了聲能量在水中運(yùn)動(dòng)，產(chǎn)生了聲學(xué)虹吸效應(yīng)，如圖3(a)和圖3(b)所示。

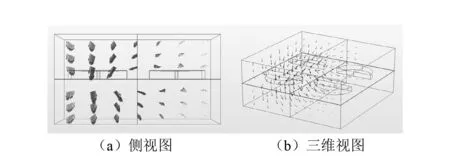
圖3 聲能量情況Fig.3 The case of sound energy

以雙元胞結(jié)構(gòu)為例，我們可以看出當(dāng)312 Hz的聲波入射時(shí)，此時(shí)的吸聲效果及阻抗匹配情況是最為理想，元胞二幾乎滿(mǎn)足阻抗匹配條件xs2≈1和ys2≈0；元胞一則可以看作是xs1≈∞ 和ys1≈1，入射波幾乎完全反射。據(jù)此得到元胞一與元胞二之間的表面壓差方程式為

Δp=-piaexp(jωt)

(14)

在這種壓差作用下，入射能量被迫從周?chē)鷧^(qū)域流到雙元胞的元胞二，更多的能量被增強(qiáng)的振動(dòng)吸收。

2.2 聲阻抗匹配機(jī)理及等效負(fù)動(dòng)態(tài)質(zhì)量密度機(jī)理

聲阻抗匹配機(jī)理是指多元胞情況下整體聲阻抗Z0對(duì)吸聲面積比η的變化不敏感，當(dāng)吸聲面積比降低時(shí)，整體結(jié)構(gòu)的聲阻抗沒(méi)有成比例增強(qiáng)。具體分析如下:

對(duì)單個(gè)元胞阻抗的理論模型進(jìn)行了分析，簡(jiǎn)化的原理圖如圖4(a)所示。單個(gè)元胞的聲阻抗是ZM，這里的薄板-質(zhì)量塊系統(tǒng)可以等效于質(zhì)量-彈簧系統(tǒng)[50]，其聲阻抗為

(15)

式中：R為由振動(dòng)強(qiáng)度決定的薄板的等效阻尼；M1取決于質(zhì)量塊的質(zhì)量；K1取決于薄板的剛度。

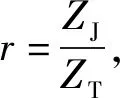
(16)

可見(jiàn)隨著面積比的減小，多元胞中的聲阻抗并沒(méi)有成比例變大。根據(jù)聲阻抗匹配機(jī)理，100%的吸聲只能通過(guò)Zrc=ρ0c0，Zim=0。其中Zre和Zim分別是Z0的實(shí)部和虛部。即在共振頻率處，具有較好的吸聲效果。

聲學(xué)虹吸效應(yīng)可以使得多元胞結(jié)構(gòu)具有較為匹配的聲阻抗，因而具有較好的吸聲效果，這對(duì)設(shè)計(jì)具有寬帶吸聲效果的緊湊結(jié)構(gòu)具有重要的研究?jī)r(jià)值。

等效負(fù)動(dòng)態(tài)質(zhì)量密度機(jī)理指的是該結(jié)構(gòu)的等效質(zhì)量密度在吸聲系數(shù)峰值所對(duì)應(yīng)的頻率處為零，如圖4(c)所示，由牛頓第二定律，可以看出當(dāng)系統(tǒng)處于零等效質(zhì)量狀態(tài)時(shí)，結(jié)構(gòu)受力時(shí)自身會(huì)產(chǎn)生一個(gè)很大的加速度，系統(tǒng)會(huì)產(chǎn)生很大的響應(yīng)，形成共振。在該結(jié)構(gòu)中我們可以把該薄板-質(zhì)量塊系統(tǒng)等效于三組元振子模型[51]如圖4(b)所示，其等效質(zhì)量密度為

圖4 系統(tǒng)模型情況Fig.4 The case of the system model

(17)

式中：M2由復(fù)合鋼板的質(zhì)量決定；m由振子的質(zhì)量決定；K2取決于薄板的剛度。

薄板類(lèi)聲學(xué)超材料的吸聲特性也是基于零等效質(zhì)量效應(yīng)，通過(guò)系統(tǒng)的共振模式產(chǎn)生大量的能量耗散從而增強(qiáng)結(jié)構(gòu)的吸聲性能。

3 面積比及主要參數(shù)對(duì)吸聲性能的影響

本節(jié)詳細(xì)研究了該薄板型超材料在不同面積比下的吸聲性能，為后續(xù)的寬帶吸聲結(jié)構(gòu)設(shè)計(jì)提供指導(dǎo)；同時(shí)對(duì)該結(jié)構(gòu)的主要影響參數(shù)進(jìn)行了研究。

3.1 不同吸聲面積比的吸聲性能

圖5 面積比對(duì)吸聲情況的影響Fig.5 The effect of area ratio on sound absorption

3.2 主要參數(shù)對(duì)吸聲性能的影響

下面我們分別研究了在吸聲面積比為η=1情況下單元胞結(jié)構(gòu)(元胞一)的薄板厚度S和質(zhì)量塊高度h1對(duì)吸聲性能的影響。

圖6(a)為不同薄板厚度S對(duì)元胞一結(jié)構(gòu)吸聲性能的影響，S依次為1.0 mm，1.1 mm，1.2 mm，1.3 mm，1.4 mm。可以發(fā)現(xiàn)，隨著S從1.0 mm增大到1.4 mm，吸聲峰值頻率逐漸向高頻移動(dòng)，仍然具有很好的吸聲效果。

圖6(b)為不同質(zhì)量塊高度h1對(duì)元胞一結(jié)構(gòu)吸聲性能的影響，在這里h1分別取元胞一原質(zhì)量塊高度的0.8倍、1.0倍、1.2倍、1.4倍和1.6倍。可見(jiàn)質(zhì)量塊的高度對(duì)峰值頻率有較大的影響。隨著質(zhì)量塊高度的增加，吸聲峰值頻率逐漸向低頻移動(dòng)，同樣具有很好的吸聲效果，這為我們向低頻吸聲的調(diào)節(jié)打下了良好的基礎(chǔ)。

圖6 主要參數(shù)對(duì)吸聲性能的影響Fig.6 Influence of main parameters on sound absorption performance

4 基于聲學(xué)虹吸效應(yīng)的水下低頻大寬帶超材料

基于上述分析，圖7(a)給出了一種由單元胞結(jié)構(gòu)平行排列組成的薄板型超材料，具體來(lái)說(shuō)，薄板型超材料的整體尺寸分別為W=150 mm，L=200 mm，H=49 mm。

通過(guò)對(duì)每個(gè)元胞結(jié)構(gòu)的大小進(jìn)行合理設(shè)計(jì)，使得每個(gè)元胞結(jié)構(gòu)盡可能利用聲學(xué)虹吸效應(yīng)，同時(shí)通過(guò)對(duì)每個(gè)元胞結(jié)構(gòu)的薄板厚度以及質(zhì)量塊的大小、位置、高度的調(diào)節(jié)，使得每個(gè)質(zhì)量塊在共振頻率處對(duì)應(yīng)一個(gè)吸聲峰值，最終實(shí)現(xiàn)了100～500 Hz的低頻大寬帶吸聲效果如圖7(b)所示。

圖7 低頻大寬帶吸聲Fig.7 Low-frequency and wide-band sound absorption

5 結(jié) 論

在本研究中，我們提出并詳細(xì)研究了基于聲學(xué)虹吸效應(yīng)的水下低頻大寬帶吸聲機(jī)理，在聲學(xué)虹吸效應(yīng)的作用下，不同面積比下的吸聲元胞可以使幾乎所有的入射聲能量通過(guò)元胞的振動(dòng)被耗散掉，使得整體仍然保持著較好的吸聲性能。我們?cè)敿?xì)分析了該超材料的壓差聲匯機(jī)理、聲阻抗匹配機(jī)理、等效負(fù)動(dòng)態(tài)質(zhì)量密度機(jī)理，驗(yàn)證了該超材料的低頻大寬帶吸聲性能。同時(shí)研究了主要參數(shù)對(duì)吸聲元胞性能的影響，得出了非常重要的規(guī)律。因此，在不受試驗(yàn)條件限制的情況下，采用一定多的元胞可以進(jìn)一步提高吸聲性能，實(shí)現(xiàn)大寬帶吸聲。總之，本研究將為水下低頻大寬帶吸聲的設(shè)計(jì)提供有效的指導(dǎo)，并顯示出巨大的水下聲波控制潛力。