ITERATIVE ALGORITHMS FOR SYSTEM OF VARIATIONAL INCLUSIONS IN HADAMARD MANIFOLDS*
Qamrul Hasan ANSARI
Department of Mathematics, Aligarh Muslim University, Aligarh 202 002, IndiaE-mail: qhansari@gmail.com
Feeroz BABU
Department of Applied Mathematics, Aligarh Muslim University, Aligarh 202 002, IndiaE-mail: firoz77b@gmail.com
D. R. SAHU
Department of Mathematics, Banaras Hindu University, Varanasi 221 005, IndiaE-mail: drsahudr@gmail.com
Abstract In this paper, we consider system of variational inclusions and its several spacial cases, namely, alternating point problems, system of variational inequalities, etc., in the setting of Hadamard manifolds. We propose an iterative algorithm for solving system of variational inclusions and study its convergence analysis. Several special cases of the proposed algorithm and convergence result are also presented. We present application to constraints minimization problems for bifunctions in the setting of Hadamard manifolds. At the end,we illustrate proposed algorithms and convergence analysis by a numerical example. The algorithms and convergence results of this paper either improve or extend known algorithms and convergence results from linear structure to Hadamard manifolds.
Key words System of variational inclusions; altering point problems; monotone vector fields; strictly pseudocontractive mappings; Hadamard manifolds
1 Introduction
It is well known that the inclusion problem 0 ∈(A+ B)(x) for set-valued map A and single-valued B is one of the powerful tools to study several real life problems, namely, image recovery, image processing, machine learning, etc. During the last decade, much attention has been paid to study the existence of solutions and to develop solution methods for inclusion problems in the setting of Riemannian / Hadamard manifolds; see, for example, [1–4, 13, 15–17] and the references therein. Recently, Zhao et al. [34] considered and studied the system of inclusion problems in the setting of Hilbert spaces. Such system includes the system of variational inequalities considered and studied by Ceng et al. [9], and altering point problem considered in [25] as special cases.
Motivated by [9, 25, 26, 34], in this paper, we consider a system of variational inclusions in the setting of Hadamard manifolds and develop some iterative algorithms for finding its solution. As a special cases of our system, we also consider system of variational inequalities and altering point problems and derive iterative algorithms for computing their solutions. It is worth to mention that system of variational inequalities could be applied to study two-person game in the setting of Hadamard manifolds. Also,the altering point problem is useful to study the intersecting point of two curves.
The present paper is organized as follows: in the next section, we gather some basic definitions and results from Riemannian / Hadamard manifolds as well as from nonlinear analysis which will be used in this paper. In Section 3,we recall the definitions of single-valued and setvalued vector fields, and define strictly pseudocontractive mapping in the setting of Hadamard manifolds. We define a property(N)and provide several examples of vector fields which satisfy this property. We consider a system of variational inclusions and some of its special cases,namely, system of variational inequalities, regularized inclusion problems, altering point problems, etc. In Section 4, we propose an iterative algorithm for solving system of variational inclusions in the setting of Hadamard manifolds. We also study the convergence analysis of the proposed algorithm and several of its special cases. Section 5 provides applications to a constraints minimization problems for bifunctions in the setting of Hadamard manifolds. The proposed algorithms and convergence results are illustrated by a numerical example in the last section.
2 Preliminaries
2.1 Basic concepts from manifolds

For the rest of the paper, unless otherwise specified, M×M is assumed to be a Hadamard manifold.
Proposition 2.1 ([28]) For all x ∈M, the exponential map expx: TxM →M is a diffeomorphism, and for any two points x,y ∈M, there exists a unique normalized geodesic γ :[0,1]→M joining x=γ(0) to y =γ(1) which is in fact a minimal geodesic defined by

A geodesic triangle Δ(x1,x2,x3) in a Hadamard manifold M is a set consisting of three points x1, x2and x3, and three minimal geodesics γijoining xito xi+1, where i = 1,2,3(mod 3).
Lemma 2.2([24]) Let Δ(x,y,z)be a geodesic triangle in a Hadamard manifold M. Then,there exist x′, y′, z′∈R2such that

2.2 Convexity in Riemannian manifolds
A subset C of a Riemannian manifold M is said to be geodesic convex if for any two points x and y in C, any geodesic joining x to y is contained in C; that is, if γ : [a,b] →M is any geodesic such that x = γ(a) and y = γ(b), then γ(at+(1-t)b) ∈C for all a,b ∈R and all t ∈[0,1].
Let C and D be two geodesic convex subsets of a Riemannian manifold M. Then the set C×D is a geodesic convex subset of M×M. Indeed, let γ1:[a,b]→M and γ2:[a,b]→M be two geodesics such that x1=γ1(a), x2=γ1(b) and y1=γ2(a), y2=γ2(b). Then,
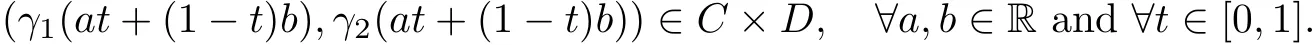


2.3 Some basic results

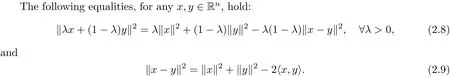
3 Formulation of System of Nonlinear Problems
3.1 Monotone vector fields and resolvent
Let Ω(M) denote the set of all single-valued vector fields B : M →T M such that B(x) ∈TxM for each x ∈M.

is called the complementary vector field of T.

3.2 Property (N)

We define the property (N) in the setting of Hadamard manifolds which was considered in[26] in the setting of Hilbert spaces / Banach spaces.


3.3 System of variational inclusions
Let A : M ?T M be a set-valued monotone vector field and let B : M →T M be a single-valued vector field. The variational inclusion problem is to find a point ˉx ∈M such that


3.4 System of variational inequalities
Let C be a nonempty closed geodesic convex subset of a Hadamard manifold M and B :C →T M be a single-valued vector field. The variational inequality problem, first considered in the setting of Hadamard manifold by N′emeth [20], is to find ˉx ∈C such that


It is considered and studied by Ceng et al. [9] when C = D in the setting of Hilbert spaces.Ceng et al. [9] proposed a relaxed extragradient method for finding a solution of the problem(3.17) in the setting of Hilbert spaces. In particular, if B1=B2=B, C = D and ˉx= ˉy, then SVI (3.17) reduces to the variational inequality problem (3.15).
4 Convergence Analysis for System of Variational Inclusions
We propose an iterative method with the help of altering point problem(3.13)and establish its convergence to a solution of SVIP (3.12). From now onwards, we assume that the solution set S of SVIP (3.12) is nonempty.








5 Application
5.1 Constraints optimization problems
Let F : M →R ∪{+∞} be a proper, lower semicontinuous and geodesic convex function with the domain D(F) := {x ∈M : F(x) /= +∞}. Let D(F) = C be a nonempty closed and geodesic convex subset of a Hadamard manifold M. The constraint minimization problem is written as



We choose the initial guesses (x1,y1)=(1,2)∈C×D and (x1,y1)=(0.1,0.3)∈C×D. Then the above algorithm converges to a unique solution (e-1/3,e-1/6) ∈C ×D of the variational inclusion problem (3.12). The iterative experiment results using software GNU Octave 4.2.2-1ubuntu1 (Intel(R) Core(TM) i5-5200U CPU @ 2.20 GHz, RAM 2.00 GB) are given in Figure 1 and Figure 2.
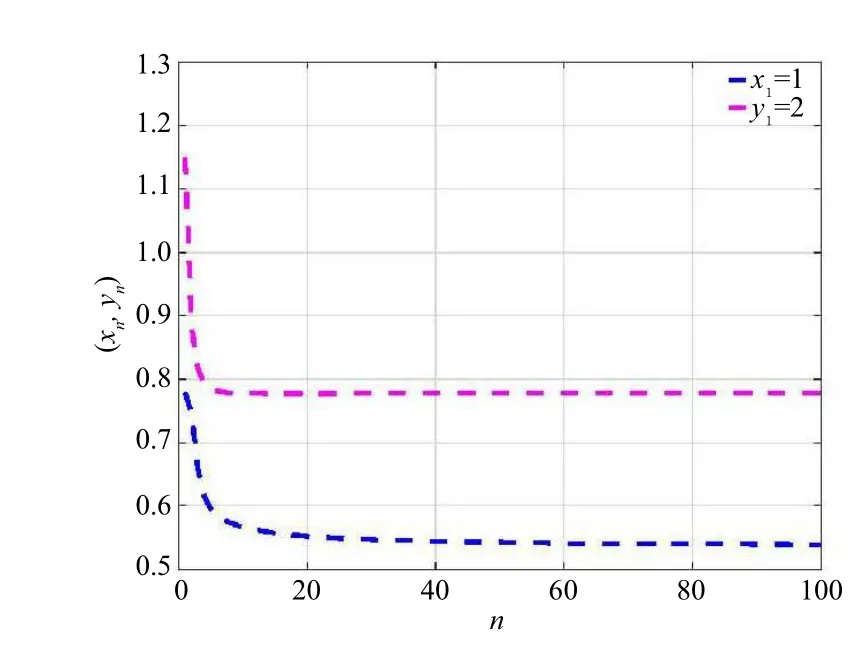
Figure 1 Convergence of Algorithm (4.1)for (x1,y1)=(1,2)
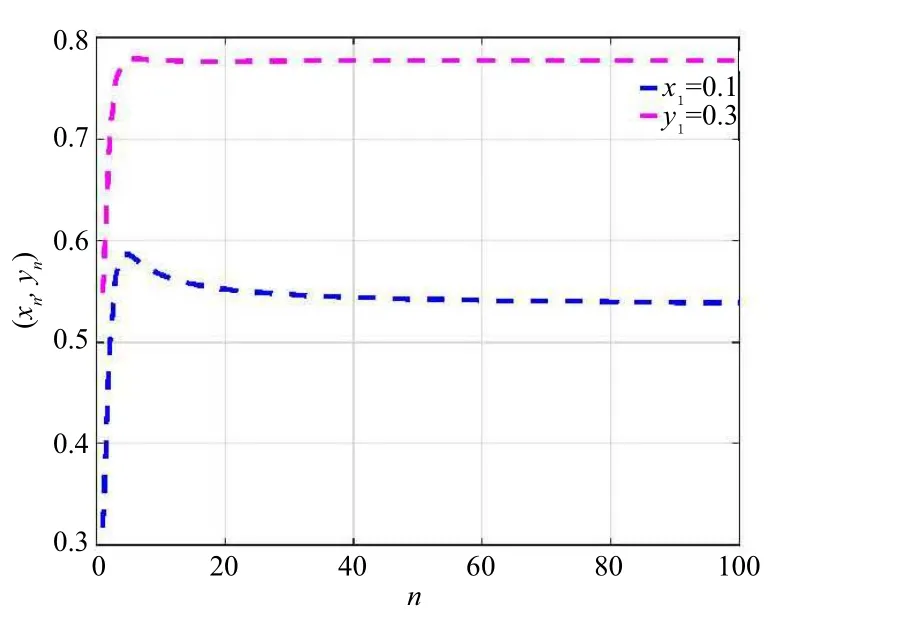
Figure 2 Convergence of Algorithm (4.1)for (x1,y1)=(0.1,0.3)
 Acta Mathematica Scientia(English Series)2022年4期
Acta Mathematica Scientia(English Series)2022年4期
- Acta Mathematica Scientia(English Series)的其它文章
- Time analyticity for the heat equation on gradient shrinking Ricci solitons
- The metric generalized inverse and its single-value selection in the pricing of contingent claims in an incomplete financial market
- The global combined quasi-neutral and zero-electron-mass limit of non-isentropic Euler-Poisson systems
- Some further results for holomorphic maps on parabolic Riemann surfaces
- Global well-posedness of the 2D Boussinesq equations with partial dissipation
- A uniqueness theorem for holomorphic mappings in the disk sharing totally geodesic hypersurfaces
