采用雙層優選策略的主動學習算法及其應用

周博文，熊偉麗,2

（1.江南大學 物聯網工程學院，江蘇 無錫 214122;2.江南大學 輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122）

在傳統機器學習建模方法中，由于環境條件的限制，采集到的樣本中通常無標簽樣本占比大，有標簽樣本占比少。為充分利用這些樣本信息，半監督學習和主動學習算法相繼提出并應用于圖像分類[1-2]、故障檢測[3-4]、工業過程建模[5-6]等領域。

傳統的半監督學習算法通過對無標簽樣本進行標記以擴大有標簽樣本集，以此達到提升模型精度的目的[7-10]。區別于半監督學習算法僅利用無標簽樣本來提升模型性能，主動學習借助專家知識，對優選出的無標簽樣本進行人工標記[11-12]，獲取其真實標簽，并將標記后的樣本加入有標簽樣本集中重新訓練模型。因此，主動學習算法的關鍵在于如何實現以最小的標記代價最大程度地提升模型的預測性能。

主動學習可劃分為基于流和基于池[13-15]兩類。基于流的主動學習通常需根據不同情況設置不同閾值實行較為困難。基于池的主動學習根據信息度量指標對無標簽樣本進行排序，挑選最具信息量的樣本進行標記。通過設置合適的評價指標可有效完成對整個無標簽樣本集的篩選。因此，許多學者圍繞基于池的主動學習進行研究，并提出多種行之有效的評價指標。如Ge 等[16]提出將主動學習與高斯過程回歸相結合，根據高斯過程回歸的預測方差衡量樣本的不確定性。Tang等[17]則利用核主成分分析進行特征提取并根據不同學習器的預測輸出挑選無標簽樣本，但該類算法通常未能兼顧到其余無標簽樣本的分布信息。Douak 等[18]則根據歐氏距離定義無標簽樣本與有標簽樣本集的差異，但該算法僅從無標簽樣本與有標簽樣本差異性角度進行選取，容易選出離群樣本。離群無標簽樣本雖與有標簽樣本差異性較大但標記后甚至會降低模型性能。為避免選出離群無標簽樣本，Rodrigue 等[19]將整個樣本集劃分為多個簇，選取聚類簇的中心樣本作為待標記樣本，Demir 等[20]則將支持向量回歸機與核k均值聚類相結合進行無標樣本的挑選，但聚類算法選出的無標簽樣本可能存在冗余且缺乏信息量。

此外，根據評價指標進行無標簽樣本的挑選，經常存在一小塊區域內多個樣本被同時選中的問題，而相似樣本一般會提供相同的信息，進行標記后造成人力物力的浪費。因此，需降低所選無標簽樣本間的冗余。綜上所述，本文提出一種帶雙層優選策略的主動學習算法，一方面根據不同模型對無標簽樣本預測輸出的差值衡量樣本的不確定性，同時引入樣本的分布信息，設計出一種新的評價指標用于無標簽樣本的挑選。另一方面，對于優選出的無標簽樣本進一步衡量樣本間的差異性并去除冗余信息。基于脫丁烷塔工業過程數據仿真，驗證了所提算法選取的樣本具有更高的信息量，可以有效地降低人工標記代價。

1 主動學習算法及建模

基于主動學習算法的機器學習建模主要包括兩個步驟：無標簽樣本的質量評估和對優選出的高質量樣本進行人工標記后建立預測模型。因此，無標簽樣本的選擇策略和有標簽樣本的建模方法是提升模型預測性能的關鍵。

1.1 無標簽樣本選擇策略

無標簽樣本選擇策略大致分為基于不確定性、差異性和代表性3 種[21-23]。不同策略的選取結果如圖1 所示，紅色樣本點為有標簽樣本，灰色為無標簽樣本，綠色樣本點為選中無標簽樣本。

圖1 主動學習樣本選擇策略Fig.1 Active learning sample selection strategy

基于不確定性的選擇策略側重于選取易被機器誤判的樣本交由人工標記；基于差異性的選取策略則側重于選取與有標簽樣本差異較大的無標簽樣本來擴大模型的預測空間；而基于代表性的選取策略核心思想為與該樣本相似的樣本越多，則該樣本的代表性越強，一般選取聚類簇中心或分布稠密處的樣本作為待標記樣本。基于不確定性和差異性的選擇策略選出的樣本都側重于擴大模型的預測空間，但容易選出離群樣本。而基于代表性的選擇策略考慮到樣本間的相似性，但選出的樣本經常彼此間存在冗余。為了克服上述問題，本文構建了一種新的評價指標，該項指標在確保樣本自身具有較高信息量的同時，還考慮到其余樣本間的分布信息，避免挑選出離群樣本。

1.2 高斯過程回歸

高斯過程回歸[24-25](Gaussian process regression,GPR)算法適用于非線性數據的建模，且模型涉及的參數少優化更加便捷。在GPR 建模中，通過選取合適的高斯核函數構建協方差矩陣，完成對樣本的預測。本文均采用平方指數函數來構建協方差函數：

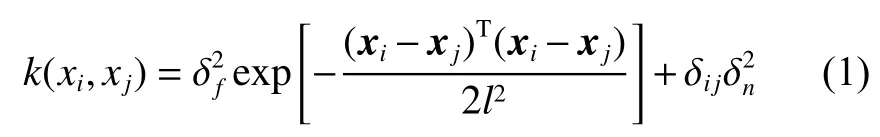
式中：δf為信號標準差；l為尺度參數；當i=j時，δij=1，否則等于0；δn為 噪聲標準差。設為模型的超參數，利用極大似然估計求得超參數最優值。

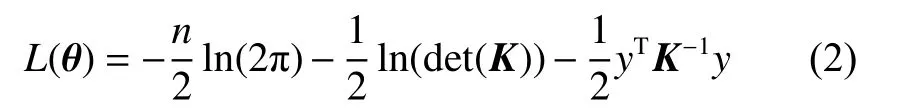
式中K為協方差矩陣，其元素Kij=k(xi,xj)。在獲得最優超參數后，對于1 個新的測試樣本xq，可根據式(3)求其預測值，根據式(4)求取方差。

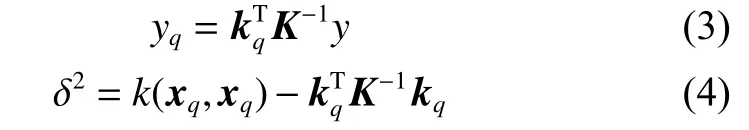
式中：yq為預測值，δ2為方差，kq=[k(xq,x1)k(xq,x2)···k(xq,xq)]T為xq與標記樣本的協方差矩陣，式(4)中k(xq,xq)為待預測樣本構建的協方差矩陣。

2 雙層優選策略下的主動學習算法

本文所提的基于雙層優選的主動學習算法，第1 層通過衡量無標簽樣本的不確定性、差異性和代表性進行優選；第2 層對優選出的無標簽樣本去除冗余信息，從而達到以較小的標記代價最大程度提升模型性能的目的。算法基本原理如圖2 所示。

圖2 雙層優選的主動學習算法Fig.2 Active learning algorithm with double-layer optimization

2.1 第1 層優選策略

在首先將有標簽樣本集均分后分別建立GPR模型 θ=abs(y1?y2) 和 θ=abs(y1?y2)，并利用這兩個模型完成對無標簽樣本的預測，分別得到預測值θ=abs(y1?y2)和 θ=abs(y1?y2)。根據差值衡量不確定性的公式為

式中：abs 為對預測值的差值取絕對值，θ為樣本不確定性度量值。θ值越大，說明不同模型對該無標簽樣本的預測分歧越大，挑選該類樣本進行標記，可有效降低預測誤差較大的樣本數目。但僅根據 θ值進行樣本的選取，未能有效利用其余無標簽樣本的信息，造成資源的浪費。

在根據不確定性進行優選的基礎上，進一步利用樣本的分布信息，判斷目標樣本與有標簽樣本的差異性和自身是否具有代表性。通常無標簽樣本的差異性和代表性會有一定的沖突，如圖3所示。紅色樣本點表示有標簽樣本，灰色樣本點表示無標簽樣本，現需選出1 個樣本進行標記后加入有標簽樣本集。顯然樣本C與有標簽樣本的差異性大于樣本A和B，但樣本點C嚴重偏離其他無標簽樣本，若選中C進行標記，甚至會降低模型預測精度。樣本A與樣本B則較為相似，對兩者信息量進行衡量，選取對模型提升最為有利的樣本。

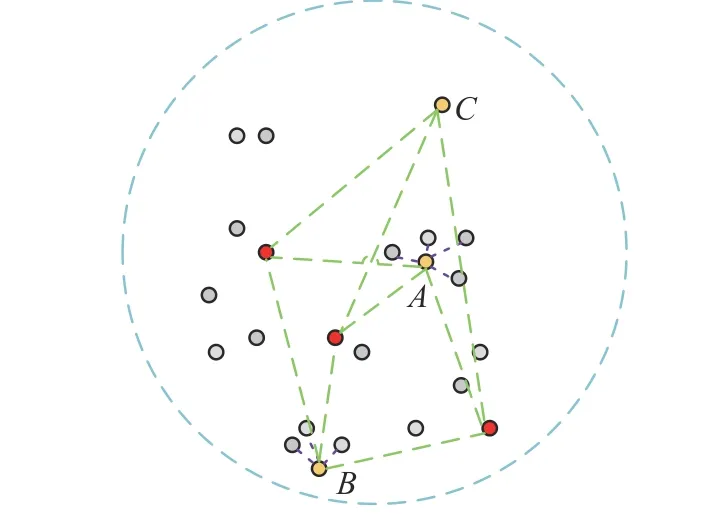
圖3 樣本的代表性與差異性Fig.3 Sample representativeness and differences

從差異性角度出發，首先根據有標簽樣本建立模型并獲取無標簽樣本預測值yp；其次計算yp與有標簽樣本真值yL的差值并取絕對值，得到Nu個無標簽樣本預測值與yL的最小差值dn；最后挑選數值較大的dn所對應的樣本，如式(6)和式(7)所示：

式中：NL和Nu分別為有標簽樣本和無標簽樣本數目。在上述迭代過程中，通過選取與yL差值較大的無標簽樣本來擴大模型的預測空間，但通常會出現部分所選樣本在分布上嚴重偏離其余無標簽樣本，進行標記后將降低模型的預測性能。為避免選出離群樣本，求取每個無標簽樣本到其余無標簽樣本的平均歐氏距離，如式(8) 和式(9)所示：

式中 δ為樣本差異性與代表性度量值。若某樣本與其余無標簽樣本的歐氏距離過大則的數值增大，即使該樣本與有標簽樣本差異顯著，也將不被選入待標記樣本。綜上分析，利用有標簽樣本的建模信息，同時將樣本的分布信息考慮其中得到第一層優選的評價指標，如公式(10)所示：

式中 α為評價指標度量值。由于 θ 與 δ兩者數量級不同，因此采用乘積形式。第一層優選過程中，在根據樣本不確定性選取的基礎上，進一步度量樣本的分布信息，判斷其對模型性能的提升是否有利。若某樣本因誤判導致預測分歧較大，而根據 δ值進行判別后發現在分布信息上不利于提升模型的預測精度，也將無法通過第一輪優選。因此，根據 α值衡量每個無標簽樣本信息量，對其進行排序后挑選出固定數目的信息量最高的樣本作為候選樣本。

2.2 第2 層優選策略

在主動學習迭代過程中，通常無標簽樣本數量大，彼此間存在信息重復，即使按照 α值挑選出信息量豐富的無標簽樣本彼此間仍會存在信息冗余，而標記相似樣本將造成人力的浪費。為此從信息冗余角度對第1 層優選出的固定數目的候選樣本進行第2 層優選。

在第1 層優選中，若設置候選樣本數過多，經過第2 層優選后雖然樣本間冗余性較低，但樣本所含信息量也隨之減少。通過設置合適的候選樣本數，使樣本整體具備較高的信息量的同時，有效擴大模型的預測空間，在去冗余后對模型性能的提升更為有利。經過多次實驗，最終確定候選樣本數為每次迭代過程中人工標記樣本數的兩倍。如圖4 所示為候選無標簽樣本分布圖，假設黃色點為通過評價指標挑選的無標簽樣本集，紅色點為有標簽樣本，綠色虛線區域則表示無標簽樣本進行標記后所拓展的模型空間。

由圖4 可以看出，選出的樣本點雖然擴大了模型空間，但部分無標簽樣本如D1、D2、D3之間相似程度較高，考慮到標記代價昂貴，若標記相似的無標簽樣本，則會造成人力物力的浪費。為避免樣本的冗余添加，使用最遠優先遍歷算法[26]進行第2 層優選，該算法的核心思想為：對于2 個樣本，它們之間距離越大則冗余性越低。算法定義如式(11)和式(12)所示：

圖4 候選樣本分布圖Fig.4 Candidate sample distribution map

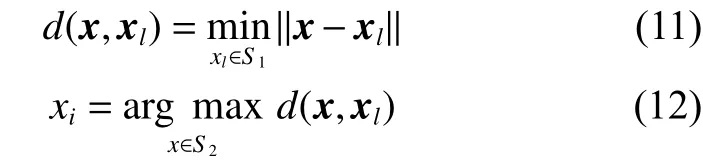
式中：S1表 示從集合S2中挑選出的待標記樣本集，S2表示候選樣本集S中剩余樣本組成的集合。該算法首先從候選樣本集S中，選擇綜合評價指標α值最大的無標簽樣本x加入待標記樣本集S1。根據式(11)和式(12)挑選下一個樣本xi加入S1，候選樣本集S則除去xi。經過二層優選得到的待標記樣本在具備信息量的同時，彼此之間差異性較大，標記后對模型的提升更為有利。

2.3 主動學習建模流程

本文提出具有雙層優選策略的主動學習算法，從不確定性、差異性、代表性3 個角度出發進行無標簽樣本的優選，并考慮樣本間的冗余信息，以全面地提升主動學習算法性能。算法流程如圖5 所示，具體建模步驟如下。

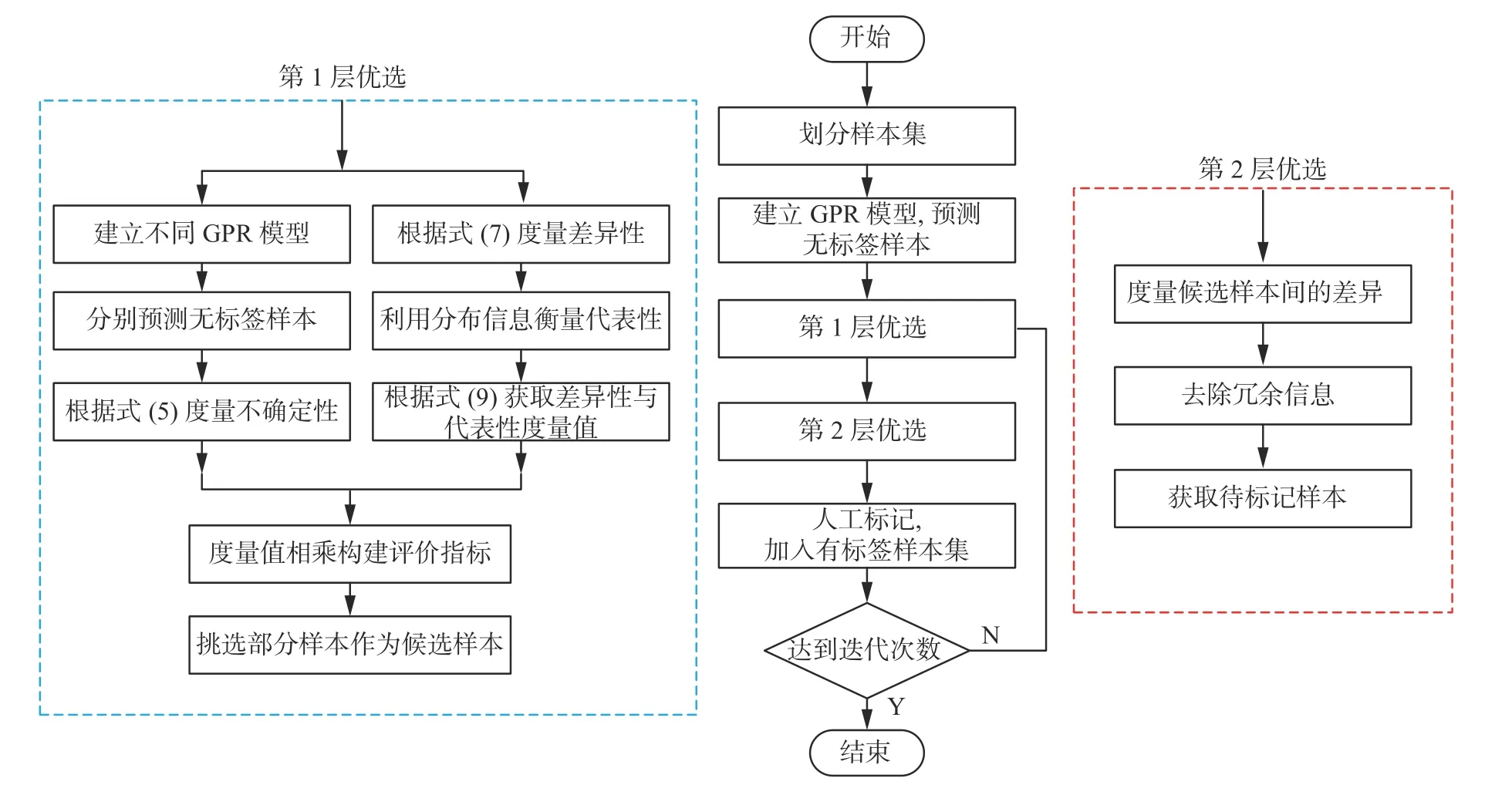
圖5 主動學習算法流程Fig.5 Active learning algorithm

1) 采集的數據集中，根據有標簽樣本建立GPR 模型，并對無標簽樣本進行預測；

2) 將有標簽樣本集均分并建立不同的GPR模型，分別對樣本進行預測，通過不同模型預測值間的差值 衡量不確定性；

3) 通過式(9)得到無標簽樣本差異性與代表性度量值，并與不確定性度量值 相乘得到評價指標。通過指標完成對無標簽樣本的第1 次優選，符合條件的樣本加入候選樣本集 ；

4) 通過最遠優先遍歷算法完成第2 次優選，選出的無標簽樣本進行人工標記后加入有標簽樣本集；

5) 更新GPR 模型，檢驗模型精度，若未達到迭代次數則返回2)，達到則停止。

3 仿真實驗

3.1 數值仿真及分析

為驗證本文所提算法的性能，與傳統的基于歐式距離的主動學習算法進行對比。為分析兩種選擇策略對于無標簽樣本選取上的區別，對函數Z=sin3X+cos3Y做回歸分析，其中X、Y均服從正態分布。數據集劃分4 組有標簽樣本集，56 組無標簽樣本集，10 組測試集。每次迭代分別選取5 個無標簽樣本進行標記。為了更好地展現2 種算法所選樣本差異，選取的無標簽樣本及樣本標記后預測誤差分布如圖6 所示。

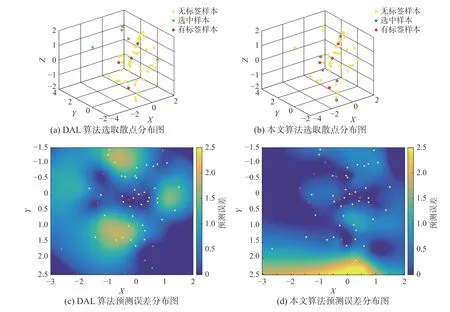
圖6 無標簽樣本選取散點及預測誤差分布圖Fig.6 Unlabeled sample selection scatter points and prediction error distribution map

圖6 中，基于歐氏距離的主動學習(distance active learning,DAL)[18]算法所選出的樣本僅考慮與有標簽樣本的差異性，選擇了部分離群點并且樣本之間存在冗余。本文算法選取的樣本則分散在模型空間中且彼此間冗余性低。進一步分析選中的無標簽樣本進行標記后，對模型預測效果的提升明顯。無標簽樣本預測誤差分布如圖(c)，(d)所示，其中紅色實心點為已標記樣本點，綠色和紫色實心點分別為根據DAL 算法和本文所提算法選擇出的樣本。黃色實心點則為無標簽樣本，色標值表示樣本的預測誤差。可以看出在已標記樣本點周圍的無標簽樣本的預測誤差都較低，而無標簽樣本附近缺少已標記樣本點則誤差會相對較高。圖(c)中在根據DAL 算法挑選部分無標簽樣本進行標記后，其余大部分無標簽樣本的預測誤差都在1 到2 之間，圖(d)中根據本文算法挑選無標簽樣本進行標記后，樣本預測誤差則在0.5～1.5。以均方根誤差[27](root mean squared error,RMSE)衡量模型預測精度，計算公式為

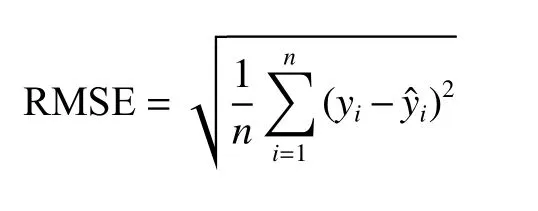
式中：n為樣本 數，yi為真值，為預測值。進 行10 次迭代，每次選取5 個無標簽樣本進行標記，模型性能隨迭代次數的變化如圖7 所示。

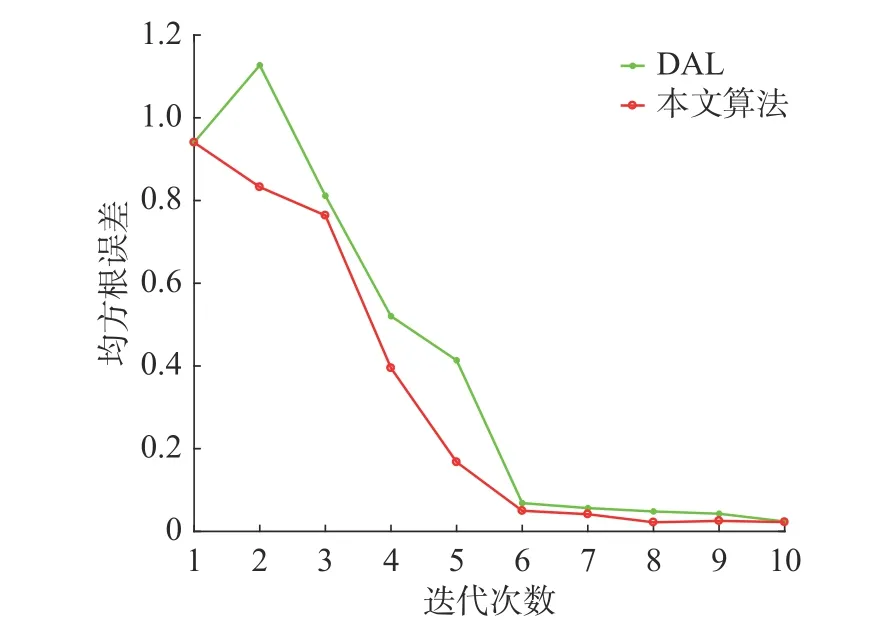
圖7 算法性能對比Fig.7 Algorithm performance contrast

從圖7 中可以看出，DAL 算法由于僅考慮樣本間的差異性，在前期迭代過程中容易選出離群樣本，而根據本文所提算法選取的無標簽樣本在擴大模型預測空間的同時自身仍具備代表性并且在經過第2 層優選后去除了樣本間的冗余信息，使所選樣本較為均勻地分散在模型空間，有效地提升了模型預測精度。

3.2 實驗仿真

以脫丁烷塔工業過程數據為對象進一步驗證算法性能。脫丁烷塔裝置如圖8 所示，脫丁烷塔在分離石油過程中是不可或缺的裝置[28]。丁烷濃度是檢測石油分離程度的一項重要指標，然而塔底的丁烷濃度難以檢測，需根據其他可監測變量建立預測模型，塔中可監測變量如表1 所示。

表1 脫丁烷塔過程變量Table 1 Process variables of the debutanizer

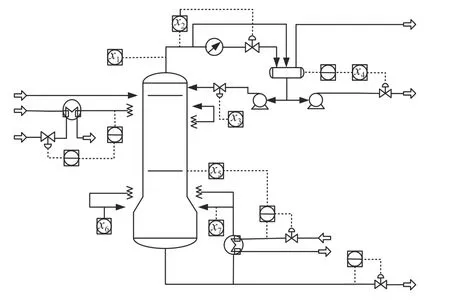
圖8 脫丁烷塔工藝流程Fig.8 Debutanizer process

實時采樣獲得2 000 組脫丁烷塔過程數據。隨機選出30 個有標簽樣本，1 800 個無標簽樣本。每次挑選50 個無標簽樣本標記后加入有標簽樣本集，另選出200 組樣本作為測試樣本。

首先，分析不同學習步長對模型性能的影響。從圖9 中可以看出較小的學習步長前期取得較好的效果，但隨著標記數目的增加，差別便不再顯著。學習步長減小意味著標記相同數目，人工標記次數增加，因此需結合實際情況進行考慮。本文重點考慮減少人工標記次數，經多次仿真實驗，最終每次選取50 個無標簽樣本進行標記。

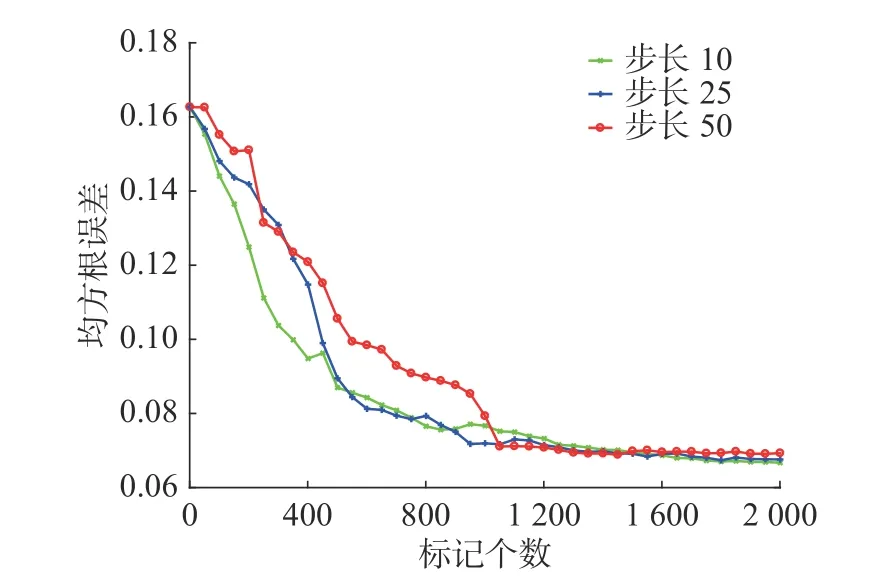
圖9 不同學習步長下模型性能變化Fig.9 Model performance changes under different learning steps

此外，對迭代過程中的評價指標變化情況進行分析。根據評價指標優選得到的無標簽樣本作為候選樣本。本文所選取的候選樣本數目為目標選取的樣本數的2 倍即選取100 個候選樣本，對候選樣本的評價指標度量值進行加和取平均，則每次迭代過程中，候選樣本的評價指標均值如圖10 所示。

圖10 迭代過程中的評價指標Fig.10 Evaluation index in iterative process

由圖10 可以看出，隨著迭代過程的進行，候選無標簽樣本的評價指標度量值越來越小，這主要是因為前期選擇的都為信息量較為豐富的無標簽樣本使剩余樣本所含的額外信息越來越少，后期因剩余無標簽樣本信息量過少，使得評價指標均值趨于停滯。這也驗證了根據評價指標進行無標簽樣本選取的可行性。

其次，分析第一層優選中各模塊對模型性能的影響，分別對不確定性指標 θ和利用樣本分布信息所獲得的差異性與代表性度量值 δ以及第一層優選中的評價指標 α進行分析。不同指標對模型的提升效果如圖11 所示。相比于指標 θ 和δ，根據評價指標 α選取的無標簽樣本，在具備較高不確定的同時，擴大了模型的預測空間，同時避免了單一角度選取的所帶來的誤判和離群點問題，因此所含信息量更為豐富。

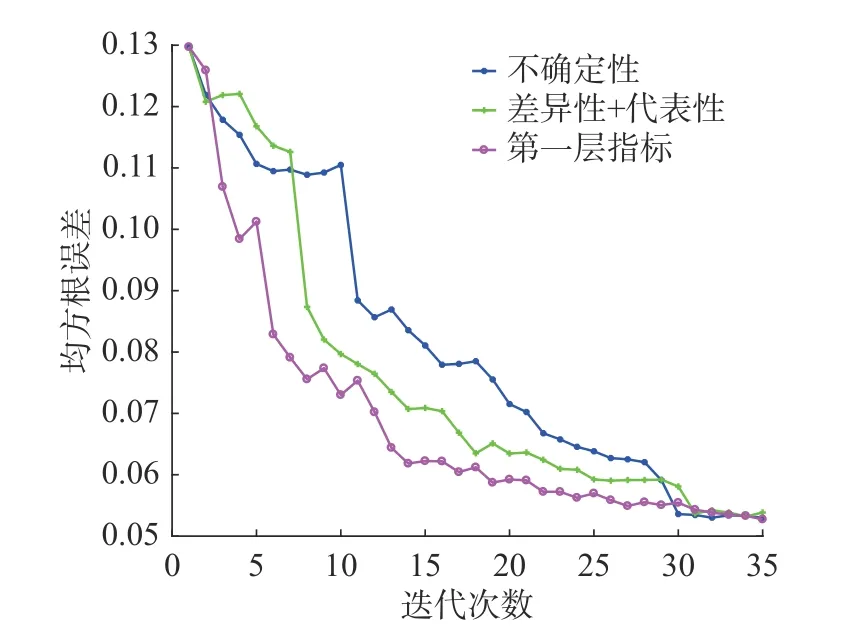
圖11 不同指標對模型性能影響Fig.11 Impact of different indicators on model performance

最后，對候選樣本去冗余后對模型性能的提升效果進行研究。通過計算樣本彼此間歐氏距離，加和后求取平均值和取其最小值相加這2 種方法來衡量經過第二層優選后樣本間的差異性。第一層優選得到100 個候選無標簽樣本雖然信息量較高，但部分樣本間存在冗余。若根據綜合評價指標選取度量值最大的前50 個樣本作為待標記樣本而不考慮彼此間的冗余，則每次迭代過程中，最小歐式距離之和如圖12(a)中藍色柱形所示，經過第二層優選后的最小歐式距離之和如圖12(a)中紅色柱形圖所示。而經過第一層優選后樣本間的平均歐氏距離如圖12(b)中藍色柱形所示，經過第二層優選后的樣本間平均歐式距離則如圖12(b)中紅色柱形圖所示。單層與雙層優選后模型性能對比如圖13 所示。

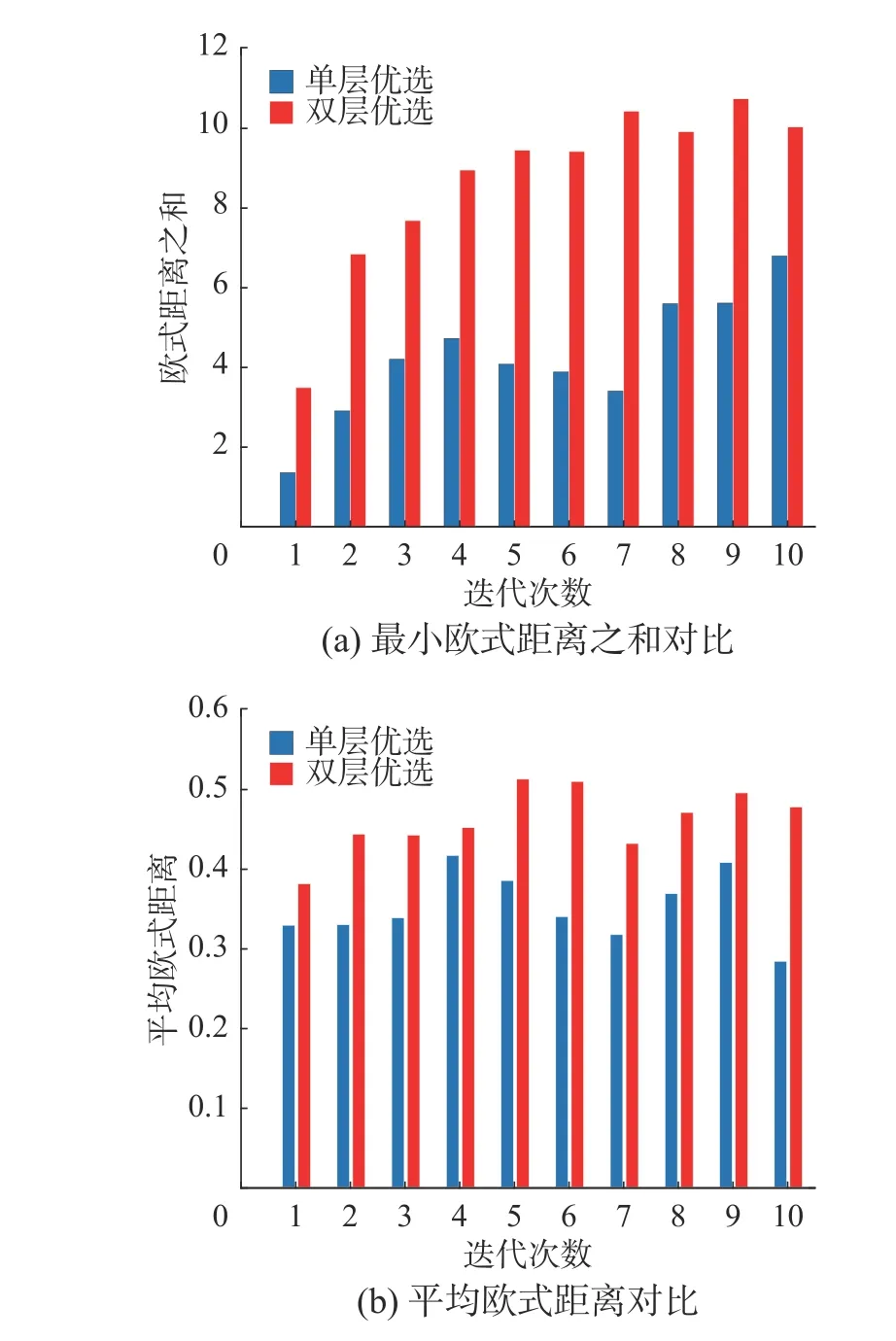
圖12 單層與雙層優選策略下樣本間差異性對比Fig.12 Comparison of differences between samples under single-layer and double-layer optimization strategies

圖13 單層與雙層優選策略對比Fig.13 Contrast of single-layer and double-layer optimization strategies

從圖12 和圖13 中可以看出，第1 層優選僅根據樣本的信息量進行選取容易造成候選樣本集內部存在冗余信息，不利于模型性能提升。第2 層的優選在保證樣本具備高信息量的同時，排除少部分具有相似信息的高質量樣本，有效地降低了樣本間的冗余，在模型迭代初期，進行人工標記后對模型效果的提升更為有利。為驗證本文所提算法有效性，與基于歐氏距離、預測值(prediction active learning,PAL)和期望變更(excepted change active learning,ECAL)3 種主動學習算法進行對比。

1) DAL[18]：以無標簽樣本與有標簽樣本間的歐氏距離作為評價指標來挑選樣本。

2) PAL[29]：有標簽樣本建模后獲取無標簽樣本預測值，預測值與有標簽樣本真值作差并以差值作為評價指標來挑選信息量較大的無標簽樣本。

3) ECAL[30]：有標簽樣本建立模型并獲取無標簽樣本的預測值，在設計損失函數后將無標簽樣本依次加入有標簽樣本集，根據損失的梯度估計樣本的不確定性。

4) 本文所提算法：每次選取50 個無標簽樣本進行標記，標記后加入有標簽樣本集，達到設置的迭代次數則停止迭代。隨機選擇初始有標簽樣本，均方根誤差如圖14(a)所示。圖14(b)則展示了隨機選擇第6 次迭代即標記250 個無標簽樣本后，4 種選擇策略的預測誤差。

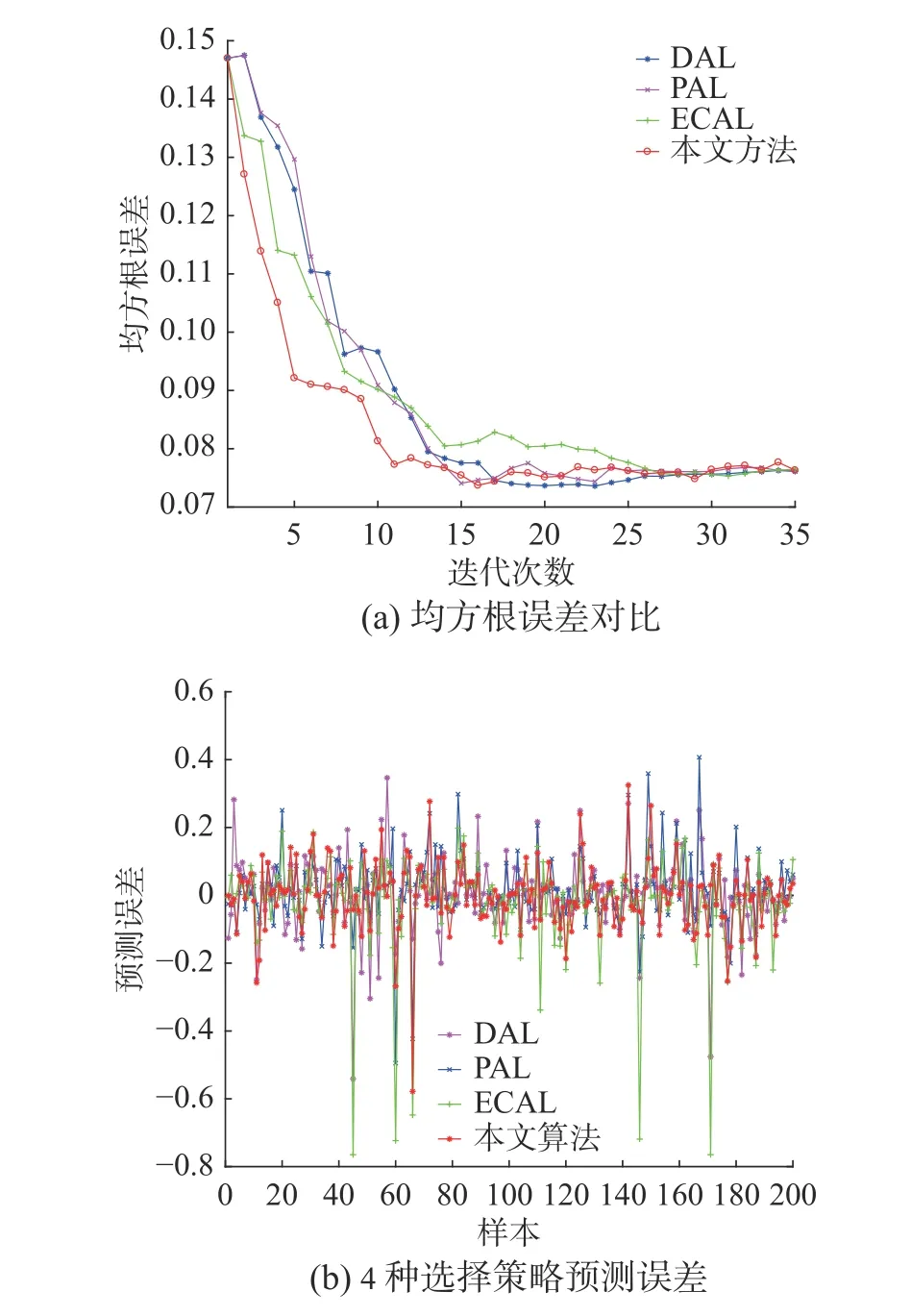
圖14 4 種主動學習算法對比Fig.14 Contrast of four active learning algorithms

從圖14(a)中可以看出，在迭代初期根據本文所提算法挑選的無標簽樣本質量要優于其他3 種算法。在后期4 種算法的下降趨勢都趨于停滯，出現這樣的現象的原因是，在前期4 種算法選擇的都為質量較高的無標簽樣本，使得后續迭代過程中剩余無標簽樣本所包含的信息量減少，對模型的提升效果不再顯著。同時本文所提算法在第11 次迭代后，再繼續添加無標簽樣本，對模型的提升效果較為有限。而要達到同樣的效果，DAL，PAL，ECAL 則要進行更多次的迭代。因此，在相同標記代價下，本文所提算法對模型提升效果更為有利。4 種主動學習算法預測丁烷濃度的指標如表2 所示，其中，ARE 為平均相對誤差，定義為

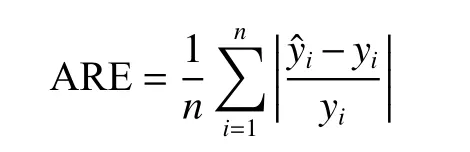
式中：n為樣本數，為預測值，yi為真值。從 表2可以看出，本文所提算法的2 個誤差評價指標都要低于其他3 種方法，表明所建立的模型具有更好的預測性能與泛化能力。

表2 4 種主動學習方法性能指標Table 2 Performance indicators of four active learning methods

4 結束語

本文提出了一種雙層優選的主動學習建模算法。該算法的第一層利用不同模型對無標簽樣本的信息量進行初步評估，并引入樣本的分布信息，構建評價指標后完成對無標簽樣本的第一次優選。在第二層對優選后的樣本去冗余，得到彼此差異性較大的無標簽樣本作為待標記樣本。通過數值仿真分析和脫丁烷塔過程的應用仿真，驗證了該選擇策略的有效性。并與現有的幾種選擇策略進行對比，實驗證明本文選擇策略更具備優越性，即在相同的人工標記消耗下獲得更高質量的無標簽樣本。