含軸承內(nèi)環(huán)間隙的轉(zhuǎn)子非線性動(dòng)力學(xué)建模

何奧迪，王曉偉

(南京航空航天大學(xué) 能源與動(dòng)力學(xué)院，江蘇 南京 210016)

0 引言

在航空發(fā)動(dòng)機(jī)軸承設(shè)計(jì)中，為補(bǔ)償熱膨脹而提供的間隙通常是轉(zhuǎn)子-軸承-底座系統(tǒng)的振動(dòng)源，并導(dǎo)致非線性動(dòng)力學(xué)行為。一般來說，間隙可存在于滾動(dòng)軸承和軸頸之間、滾動(dòng)軸承或軸承外圈和底座之間或者就是軸承的游隙。

YAMAMOTO T將軸承間隙的非線性引入轉(zhuǎn)子-軸承系統(tǒng)的Jeffcott方程。結(jié)果表明：隨著軸承間隙的增大，臨界轉(zhuǎn)速的最大振幅和臨界轉(zhuǎn)速的值將減小[1]。SAITO S[2]研究了含徑滾珠軸承支承水平Jeffcott轉(zhuǎn)子的非線性不平衡響應(yīng)[2]。雖然上述兩項(xiàng)研究?jī)H涉及諧波響應(yīng)分析，但CHOI Y S等采用諧波平衡法和離散傅里葉變換方法分析了轉(zhuǎn)子-軸承模型中的超諧波和次諧波的相干性[3]。ISHIDA Y研究了軸承外環(huán)與殼體之間存在徑向間隙的柔性轉(zhuǎn)子系統(tǒng)中的振動(dòng)問題，并通過豎直偏置盤轉(zhuǎn)子振動(dòng)實(shí)驗(yàn)，發(fā)現(xiàn)在大于主臨界轉(zhuǎn)速的大范圍轉(zhuǎn)速內(nèi)，正渦動(dòng)的自激振動(dòng)振幅幾乎保持不變，但是在某些特定的轉(zhuǎn)速下，自激振動(dòng)消失，取而代之的是非線性振動(dòng)現(xiàn)象。這種現(xiàn)象被稱為夾帶現(xiàn)象，這些非線性振動(dòng)為次諧波振動(dòng)超次諧波振動(dòng)和組合振動(dòng)[4-5]。ISHIDA Y通過諧波平衡法(HBM)分析了非線性動(dòng)力學(xué)模型的周期解，從理論上證實(shí)了這些非線性振動(dòng)現(xiàn)象的存在，也證明了次諧波振動(dòng)時(shí)夾帶現(xiàn)象的存在[6]。KAPPAGANTHU K等提出了一種考慮軸承內(nèi)游隙和波紋度影響的球軸承支承轉(zhuǎn)子系統(tǒng)五自由度動(dòng)力學(xué)模型。在此基礎(chǔ)上，研究了轉(zhuǎn)子-軸承系統(tǒng)的穩(wěn)定性和動(dòng)態(tài)特性[7]。陳誠(chéng)等通過建立在軸承氣膜力和箔片摩擦力共同作用下的轉(zhuǎn)子局部受力模型，分析了轉(zhuǎn)速對(duì)轉(zhuǎn)子非線性動(dòng)力學(xué)性能的影響[8]。

目前關(guān)于軸承內(nèi)環(huán)與軸頸之間存在間隙的轉(zhuǎn)子動(dòng)力學(xué)研究文章較少。本文針對(duì)某航空發(fā)動(dòng)機(jī)設(shè)計(jì)過程中的軸承內(nèi)環(huán)間隙設(shè)計(jì)問題，設(shè)計(jì)了一個(gè)試驗(yàn)器，建立了盤-軸頸二自由度間隙支承轉(zhuǎn)子非線性動(dòng)力學(xué)模型，研究轉(zhuǎn)子軸頸與軸承內(nèi)環(huán)的配合間隙對(duì)轉(zhuǎn)子動(dòng)力學(xué)特性的影響規(guī)律。

1 軸承內(nèi)環(huán)間隙支承轉(zhuǎn)子非線性動(dòng)力學(xué)建模

在某航空發(fā)動(dòng)機(jī)中，軸承內(nèi)環(huán)與軸頸之間采用間隙配合，為了研究軸承內(nèi)環(huán)間隙對(duì)轉(zhuǎn)子動(dòng)力學(xué)的影響，設(shè)計(jì)了如圖1所示的偏執(zhí)單盤轉(zhuǎn)子系統(tǒng)。在轉(zhuǎn)子右端支承處，采用了含軸承內(nèi)環(huán)間隙的裝配方式，右端軸頸可以在間隙中移動(dòng)。

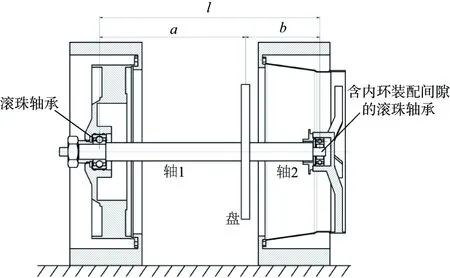
圖1 內(nèi)環(huán)間隙配合轉(zhuǎn)子系統(tǒng)示意圖

在非線性動(dòng)力學(xué)建模過程中，引入如下假設(shè)：1)軸承無(wú)游隙，軸承外環(huán)和軸承座無(wú)間隙，軸承內(nèi)環(huán)支承在彈性支承上，可自由轉(zhuǎn)動(dòng)；2)在不平衡力作用下軸頸一直沿軸承內(nèi)環(huán)內(nèi)表面運(yùn)動(dòng)；3)軸承內(nèi)環(huán)與軸徑不發(fā)生打滑。

將內(nèi)環(huán)間隙配合轉(zhuǎn)子系統(tǒng)簡(jiǎn)化為盤-軸頸二自由度間隙支承轉(zhuǎn)子非線性碰撞模型，簡(jiǎn)化準(zhǔn)則為：保留右端軸頸的質(zhì)量，忽略軸的質(zhì)量，只考慮軸的剛度。簡(jiǎn)化后的內(nèi)環(huán)間隙轉(zhuǎn)子二自由度模型如圖2所示。

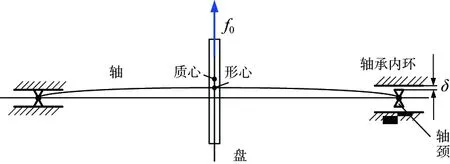
圖2 二自由度內(nèi)環(huán)間隙轉(zhuǎn)子模型

為了保持固有頻率隨轉(zhuǎn)速的變化，添加陀螺力矩項(xiàng)，轉(zhuǎn)盤、軸頸在轉(zhuǎn)子模型位置如圖3所示。

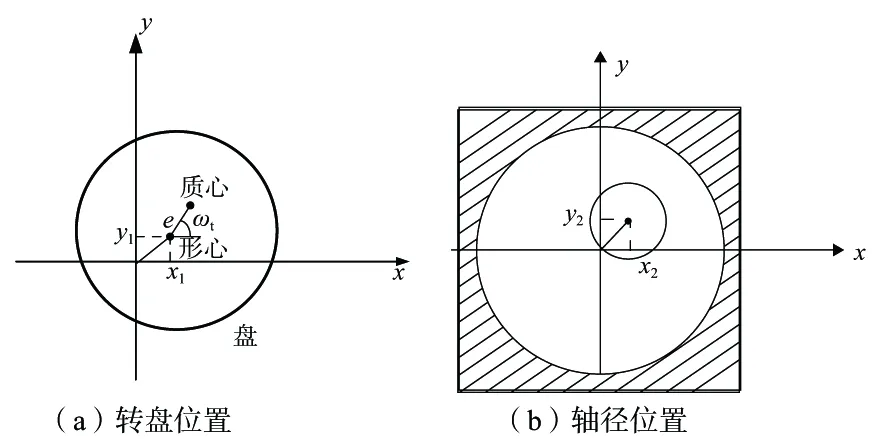
圖3 轉(zhuǎn)盤、軸頸在轉(zhuǎn)子模型位置

二自由度內(nèi)環(huán)間隙轉(zhuǎn)子動(dòng)力學(xué)方程如下：

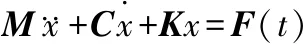
(1)

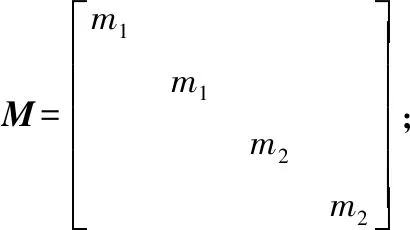
傳感網(wǎng)絡(luò)技術(shù)是由傳感器組成的網(wǎng)絡(luò)，主要包括數(shù)據(jù)處理單位部件、傳感器和通信部件等，在其工作過程中，能夠隨機(jī)分布在需要采集并傳輸信息的領(lǐng)域中，且不同點(diǎn)之間相互聯(lián)系，共同組成一個(gè)網(wǎng)絡(luò)結(jié)構(gòu)。在傳感器中存在大量的節(jié)點(diǎn)，這些點(diǎn)分布較為隨機(jī)，節(jié)點(diǎn)密集，具有較強(qiáng)的環(huán)境適應(yīng)性，因而需要其具有一定的能量存儲(chǔ)功能，這樣才能保證傳感器的正常運(yùn)行。傳感器在物聯(lián)網(wǎng)技術(shù)中發(fā)揮著重要作用，從某種角度上說，傳感器是物聯(lián)網(wǎng)技術(shù)的核心，能夠?qū)崿F(xiàn)其應(yīng)用層、傳輸層和信息感知層之間的連接，從而最終實(shí)現(xiàn)人與物、人與人之間的信息傳輸和交換。

x=[x1y1x2y2]T；

式中：m1和m2分別為轉(zhuǎn)盤和右軸頸的質(zhì)量；x1、y1和x2、y2分別為圓盤和右軸頸在xy平面上的位移；c1、c2分別為轉(zhuǎn)盤和右軸頸的阻尼系數(shù)；ipω和-ipω為陀螺力矩項(xiàng)；f0為模擬軸承裝配誤差引起的橫向靜載荷；e為偏心距；ω為轉(zhuǎn)子轉(zhuǎn)速；t為時(shí)間；ks1和ks2分別為轉(zhuǎn)軸的彈性系數(shù)，可以由式(2)得到：

(2)

式中：Es是轉(zhuǎn)子的彈性模量；Is是轉(zhuǎn)子橫截面積的慣性矩。

式(1)中不含軸徑碰撞項(xiàng)。為了使方程更接近實(shí)際情況，將添加軸頸和軸承內(nèi)環(huán)之間的碰撞模型。模型采用文獻(xiàn)[6]的模型進(jìn)行描述，碰撞模型如圖 4所示。

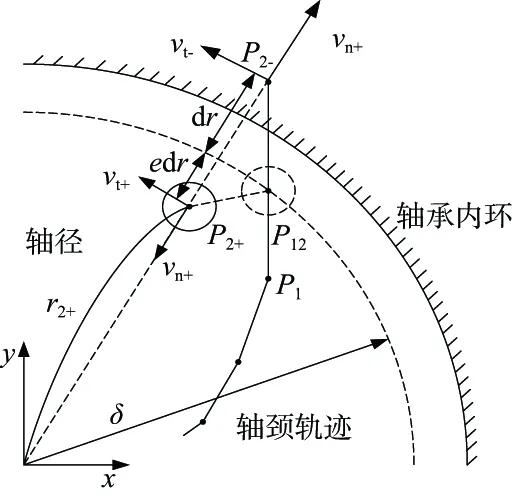
圖4 軸徑軸承碰撞模型

在圖4中，為了便于解釋，軸頸相對(duì)于軸承內(nèi)環(huán)略圖較小，r2是軸頸的徑向位移，vn和vt分別是軸頸在法向和切向方向上的速度分量。在數(shù)值仿真中，軸承軌跡由一系列離散點(diǎn)給出。P2+假設(shè)軸徑沿軸承內(nèi)環(huán)壁移動(dòng)，P1是碰撞前一步的離散點(diǎn)。離散點(diǎn)P2-為內(nèi)環(huán)壁外的投影點(diǎn)，假設(shè)軸頸在P12位置發(fā)生碰撞，然后被反彈至位置P2+。P2+處軸頸的速度和徑向位移表示如下：

(3)

因?yàn)樵趧?dòng)力學(xué)方程中很難表述圖 4所示的碰撞模型，所以采用等效彈簧和阻尼來模擬軸頸與軸承內(nèi)環(huán)的碰撞，將碰撞轉(zhuǎn)換為瞬時(shí)黏彈性變形。當(dāng)軸頸與軸承內(nèi)環(huán)發(fā)生碰撞時(shí)，在碰撞點(diǎn)軸頸會(huì)受到一個(gè)徑向的碰撞力，該碰撞力Fn表示為

(4)

式中kbn、cbn分別為彈簧和阻尼系數(shù)，θ=tan-1(y2/x2)。

(5)

構(gòu)建如下等式：

(6)

通過式(6)對(duì)式(1)進(jìn)行無(wú)量綱處理。在式(6)中，設(shè)d0為轉(zhuǎn)子系統(tǒng)的單位長(zhǎng)度。為了方便表述，將處理后無(wú)量綱公式中的 ' 略去，最終得到帶碰撞邊界條件的轉(zhuǎn)子間隙支承系統(tǒng)的無(wú)量綱動(dòng)力學(xué)方程為

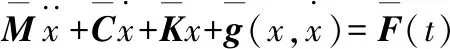
(7)

式中：

2 間隙支承轉(zhuǎn)子非線性動(dòng)力學(xué)仿真

在上節(jié)建立了二自由度間隙支承轉(zhuǎn)子非線性碰撞模型，分析間隙的大小對(duì)轉(zhuǎn)子振動(dòng)特性的影響，采用MATLAB中的ODE45求解器求解，單盤轉(zhuǎn)子系統(tǒng)參數(shù)如表 1所示。

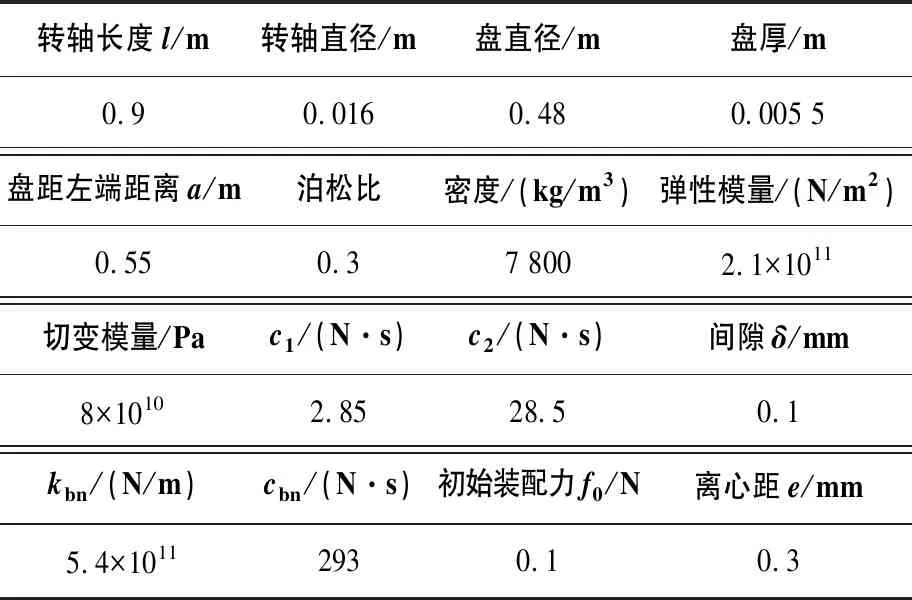
表1 單盤轉(zhuǎn)子系統(tǒng)參數(shù)

因?yàn)檗D(zhuǎn)子系統(tǒng)前期為不穩(wěn)定狀態(tài)，所以取后1/5時(shí)間段內(nèi)的振動(dòng)響應(yīng)曲線來代表系統(tǒng)的動(dòng)力學(xué)特性，如圖 5所示。

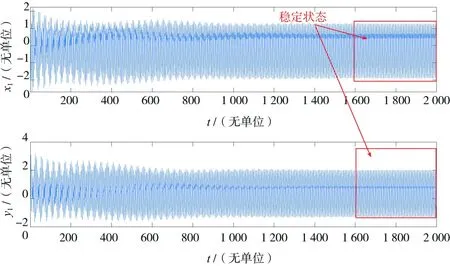
圖5 圓盤在x和y方向上的位移時(shí)域圖

通過數(shù)值仿真得到該轉(zhuǎn)子系統(tǒng)的Bode圖。可以觀察到隨著轉(zhuǎn)速的增加，圓盤的振幅出現(xiàn)了許多峰值點(diǎn)，用圓圈標(biāo)出。可以確定，在這些峰值點(diǎn)附近轉(zhuǎn)子系統(tǒng)發(fā)生了非線性振動(dòng)，研究這些振幅峰值轉(zhuǎn)速下轉(zhuǎn)子間隙支承系統(tǒng)的動(dòng)力學(xué)特性，得到圖 6所示的一系列曲線。

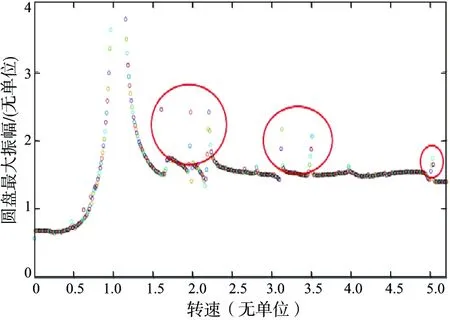
圖6 轉(zhuǎn)子系統(tǒng)的Bode圖

為了方便理解，將無(wú)量綱轉(zhuǎn)速ω替換為頻率比λ。圖 7(a)為組合振動(dòng)[pf-pb]。[]表示當(dāng)頻率比為λ=pf-pb附近時(shí)發(fā)生的組合振動(dòng)類型。當(dāng)發(fā)生這類組合振動(dòng)時(shí)，因?yàn)閜f/pb為無(wú)理數(shù)，所以此時(shí)圓盤的運(yùn)動(dòng)軌跡為非周期性。圖 7(c)為1/2階次諧波振動(dòng)。從頻譜圖可以看出，除了存在頻率比為λ=+1的諧波振動(dòng)外，還分別存在振動(dòng)頻率為+(1/2)正進(jìn)動(dòng)頻率，圓盤的振動(dòng)為諧波振動(dòng)與次諧波振動(dòng)疊加后的強(qiáng)迫振動(dòng)。因?yàn)檫@些次諧波振動(dòng)頻率與諧波振動(dòng)頻率之間為特殊的整數(shù)倍比例關(guān)系，所以圓盤的軌道圖為周期的簡(jiǎn)單閉環(huán)，軸頸是貼著軸承內(nèi)環(huán)滑動(dòng)的。圖 7(d)為+(2/5)超次諧波振動(dòng)。因?yàn)槌沃C波振動(dòng)頻率與諧波振動(dòng)頻率之間關(guān)系的特殊性，所以當(dāng)發(fā)生超次諧波振動(dòng)時(shí)，圓盤的軌道圖由周期且較復(fù)雜的閉環(huán)組成，軸頸與軸承內(nèi)環(huán)反復(fù)碰撞。

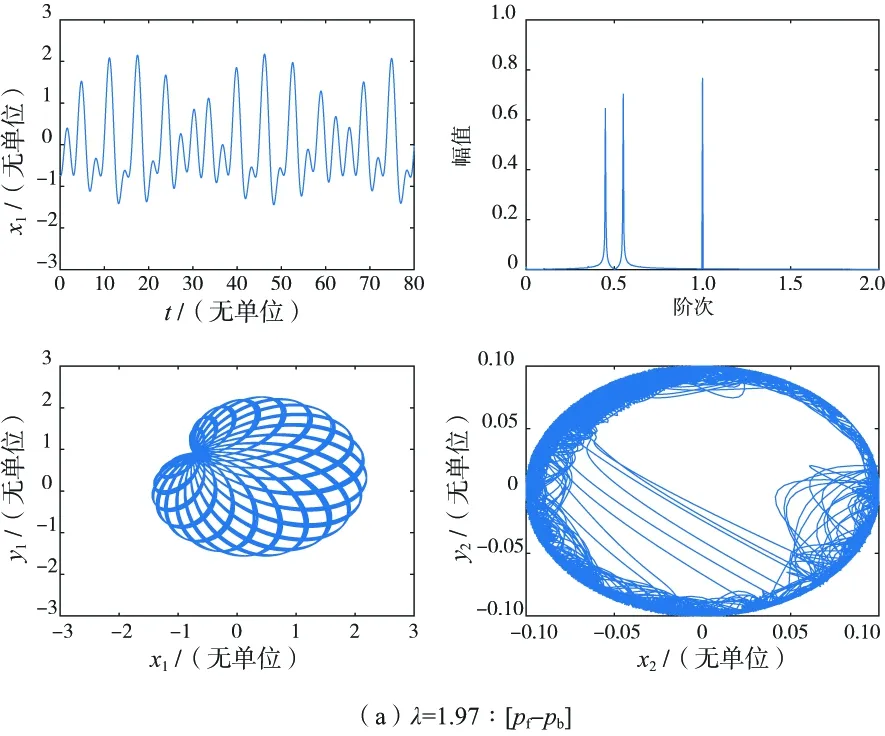
圖7 特定轉(zhuǎn)速下轉(zhuǎn)子系統(tǒng)的時(shí)域圖、頻譜圖和軌道圖

改變軸承內(nèi)環(huán)間隙大小，圓盤不同共振類型振幅如表2所示，不同間隙下圓盤Bode圖如圖8所示。

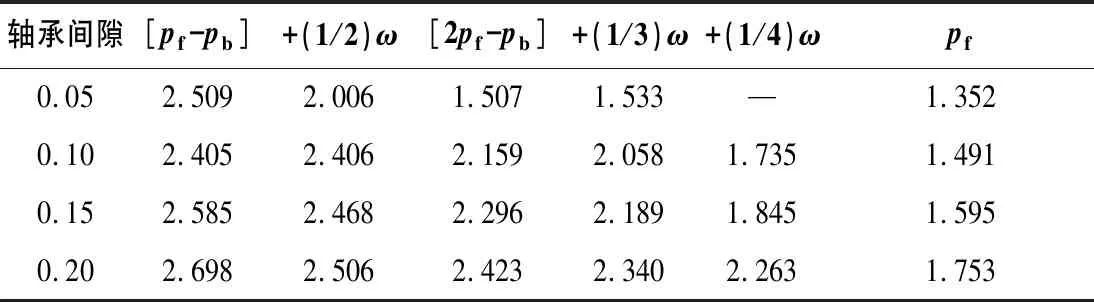
表2 不同間隙大小時(shí)不同共振類型的振幅

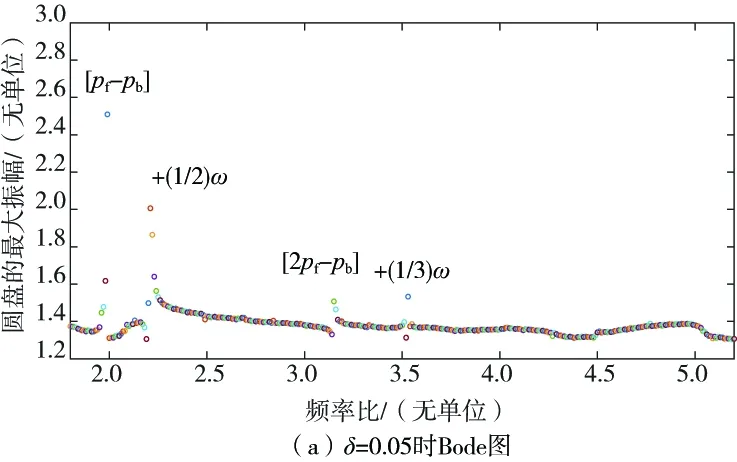
圖8 不同間隙下圓盤Bode圖

從表2可以看出，隨著軸承內(nèi)環(huán)與軸頸的間隙不斷增大，組合振動(dòng)[pf-pb]的振幅幾乎不變，其他組合振動(dòng)和次諧波振動(dòng)的振幅呈增大的趨勢(shì)。同時(shí)可以看出，伴隨著軸承內(nèi)環(huán)間隙的增大，轉(zhuǎn)子系統(tǒng)會(huì)出現(xiàn)一些新的非線性振動(dòng)，例如，當(dāng)軸承內(nèi)環(huán)間隙δ=0.10時(shí)，在4倍轉(zhuǎn)速左右出現(xiàn)了振幅較小的3/10階的超次諧波振動(dòng)。當(dāng)軸承內(nèi)環(huán)間隙δ=0.15時(shí)，出現(xiàn)2/7階的超次諧波振動(dòng)。當(dāng)軸承內(nèi)環(huán)間隙δ=0.20時(shí)，新出現(xiàn)了2/5階的超次諧波振動(dòng)現(xiàn)象。由此可以得出結(jié)論，軸承內(nèi)環(huán)間隙越大，間隙支承系統(tǒng)的非線性振動(dòng)越為復(fù)雜，會(huì)出現(xiàn)一系列非線性振動(dòng)，所以減小軸承內(nèi)環(huán)間隙能有效地抑制轉(zhuǎn)子支承系統(tǒng)的非線性振動(dòng)。

3 結(jié)語(yǔ)

本文以航空發(fā)動(dòng)機(jī)轉(zhuǎn)子間隙支承結(jié)構(gòu)為研究對(duì)象，建立了考慮軸頸和軸承內(nèi)環(huán)間存在碰撞的動(dòng)力學(xué)模型，并通過數(shù)值仿真研究了間隙支承結(jié)構(gòu)的非線性振動(dòng)現(xiàn)象，并得到以下結(jié)論：

1)間隙支承系統(tǒng)在超臨界狀態(tài)下會(huì)出現(xiàn)一系列非線性振動(dòng)，包括自激振動(dòng)、次諧波振動(dòng)、組合振動(dòng)和超次諧波振動(dòng)；

2)間隙支承系統(tǒng)發(fā)生次諧波振動(dòng)時(shí)，軸頸貼著軸承內(nèi)環(huán)滑動(dòng)，圓盤軌跡為周期性的簡(jiǎn)單圓環(huán)。發(fā)生超次諧波振動(dòng)時(shí)和組合振動(dòng)時(shí)，軸頸與軸承內(nèi)環(huán)不斷碰撞；

3)研究了間隙和支承剛度這些因素對(duì)轉(zhuǎn)子間隙支承系統(tǒng)動(dòng)力學(xué)特性的影響規(guī)律。軸承內(nèi)環(huán)間隙對(duì)轉(zhuǎn)子動(dòng)力學(xué)特性有一定影響，減小軸承內(nèi)環(huán)與軸頸的間隙大小能減弱轉(zhuǎn)子的非線性振動(dòng)特性。