網架結構單點沖擊激勵的數學模型與數值分析

鄒 韜, 蔡曉麗, 伍曉順

(江西理工大學 土木與測繪工程學院(南昌)， 南昌 330013)

大跨空間結構[1-3]類型豐富，服役數量多。由于跨度大、覆蓋面積廣，此類結構一旦破壞將產生嚴重后果。因此，應當對此類結構進行健康監測以便及時判斷結構損傷和保證結構安全。動力測試是結構健康監測領域常用的技術手段，但該方法在應用于大跨空間結構時常遇到激振難題[4-5]。

目前大跨空間結構的激振方式大致可以分為兩類。第一類是環境激勵[6-9]，主要指風振激勵。有些文獻提到可以采用地震激勵[10-11]，但地震激勵在現實中遇到的概率較低。環境激勵具有無需激振設備且激振能量大的優點，但也存在每次激勵時被激發模態不固定、有時難以激發目標模態的缺點。第二類是人工激勵，包括錘擊激勵、激振器激勵、跳躍激勵和階躍激勵等[12-16]。錘擊激勵利用力錘來激發結構的振動，輸入能量小且難以保證激勵方向。激振器激勵可以輸入較大能量，但在現場測試中設備安裝較為困難。跳躍激勵利用少數人在屋面上的跳躍激發結構的振動，可以主動控制跳躍的位置和快慢。階躍激勵采用突卸重物的方式使結構產生具有初始位移的自由振動，可以通過優化荷載分布激發特定模態。總的來說，錘擊激勵和激振器激勵適用于室內模型試驗，并不適用實際結構的現場測試。相比跳躍激勵，階躍激勵可以較為精確地控制荷載分布從而實現激發特定模態的目的。但是，階躍激勵的激振效率較低，往往需要施加較大的重物荷載才能激發出較大的加速度幅值。

一般而言，較大的加速度幅值有利于增大采集信號的信噪比[17]，從而提高模態識別、模型修正和損傷識別等工作的精度。為了盡量利用較小的重物質量來使結構產生較大的加速度幅值，有必要對基于重物墜落的沖擊激勵新方法展開定量研究。本文將重物、繩索和結構視作一個模擬單點沖擊激勵的復雜振動系統，并推導該系統的振動方程。在求解振動方程得到單點沖擊力時程的數學表達式后，以某1 200桿網架結構為例進行數值分析。重點考察重物質量、墜落高度、繩索彈性模量、繩索剛度和等效振動系統阻尼比對結構最大加速度幅值的影響，并與階躍激勵進行對比。

1 單點沖擊激勵的數學模型

1.1 模擬單點沖擊激勵的復雜振動系統

對于大跨空間結構，可以采用使重物突然墜落的方式對其施加沖擊激勵。基本流程為：① 懸掛重物，在激勵位置(為豎向)懸掛重物，用繩索連接重物與節點處電磁鐵，并將重物與松弛繩索抬高s1。② 釋放重物，在重力作用下重物自由墜落，直到繩索張緊并達到足夠大的沖擊力將電磁鐵拉開后結構開始振動。可以通過調整電壓來設定不同的電磁鐵吸力[18]。

在繩索剛張緊的瞬間，重物具有最大動能，且尚未傳遞給繩索。此時，根據能量守恒原理，重物的初速度為

(1)

式中：g為重力加速度；s1為繩索從開始墜落到繩索剛張緊瞬間的墜落高度。

繩索張緊后，重物下墜產生的動能將通過繩索傳遞到結構，使重物、繩索和結構一起發生振動。由于結構上的懸掛點存在有限剛度，因此懸掛點不能視作無限剛的邊界，而應當視作一個彈簧(稱為彈簧1)。彈簧1的剛度等于懸掛點(即激振點)對應自由度的結構剛度，且質量為零。張緊后的繩索也可視作一個彈簧(稱為彈簧2)。彈簧2的剛度等于繩索的軸向剛度，其質量沿軸向均勻分布。可見，重物和兩個彈簧構成了一個具有集中質量和分布質量的復雜振動系統，如圖1所示。

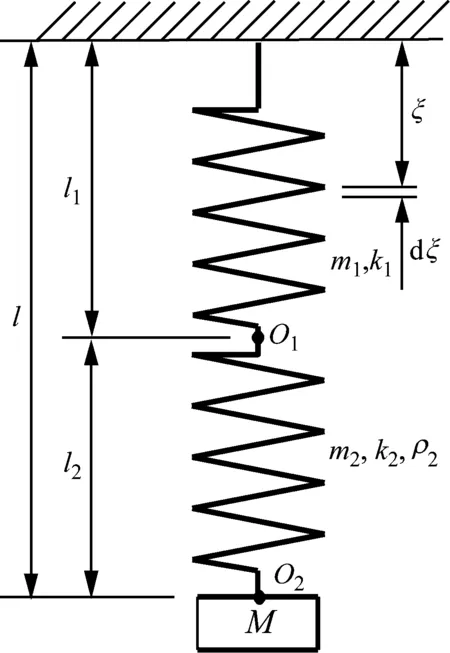
圖1 重物、繩索和結構構成的模擬單點沖擊激勵的復雜振動系統

Fig.1 Complicated system to simulate single-point impact excitation, which is composed of the weight, the cable and the structure

圖1所示振動系統的參數簡述如下：彈簧1的剛度、質量和長度分別記為k1，m1和l1；彈簧2的剛度、質量密度、質量和長度分別記為k2，ρ2，m2和l2；重物質量記為M。根據前述分析，可知m1=0，m2=ρ2l2。以繩索剛張緊時重物所在位置為零位移位置，并以坐標向下為正。

1.2 復雜振動系統的振動方程

忽略繩索質量對等效剛度k的響應，根據力的平衡方程，有

(2)

式中：u1，u2和u分別為O1，O2和O點的位移；u2=u。整理式(2)后分別得到

(3)

(4)

假設彈簧1、彈簧2在運動過程中是均勻變形的，彈簧1、彈簧2中任意一點距固定端ξ處的位移分別為

(5)

(6)

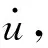
dT1=0,ξ∈[0,l1]

(7)

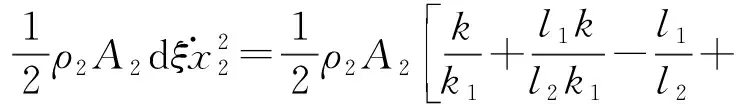
(8)

在t時刻，振動系統的動能等于重物和2個彈簧的動能之和，具體表達式為

(9)

在t時刻，振動系統的勢能為

(10)

非保守力(重力可視作幅值為常數的外部激勵)做功的變分為

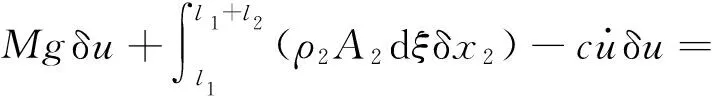
(11)

將式(9)～式(11)代入Hamilton原理[19]

(12)

整理后得到振動方程為

(13)

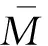
2.3 沖擊激勵的時程

由式(13)得到振動系統的位移解為

(14)

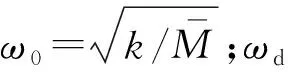
(15)

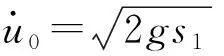
(16)

(17)

式(16)、式(17)表明振動系統為簡諧振動。在t≤0.5π/ωd時(即前1/4周期)，繩索張力的時程為

F=ku(t)=k1u1(t)

(18)

當t=0.5π/ωd時(即1/4自振周期處)，點O1處的位移u1達到最大值

(19)

相應地，沖擊力在t=0.5π/ωd時達到最大，為Fmax=k1u1 max。通過調整電壓，將懸掛點處電磁鐵的最大承載力設置為Bmax=γk1u1 max，其中γ為不大于1的折減系數。在繩索張力達到Bmax時，繩索脫離電磁鐵，對結構完成沖擊激勵并使結構開始自由振動。

2 數值算例

2.1 模型參數

以某60 m×45 m的正放四角錐平板網架為例進行數值分析，如圖2所示。網架的結點數為326(其中支座結點數為16)，桿件數為1 200。考慮3種荷載工況(包括0.25 kN/m2靜載、0.3 kN/m2活載和-0.5 kN/m2風載)，基于現行設計規范[20-21]進行網架的結構設計，以盡量貼近工程實際。桿件均為二力桿，采用的圓鋼管規格從P75.5×3.75～P159.0×7.00不等。結點均為鉸接點，采用直徑為140～350 mm不等的螺栓球。鋼材等級為Q235B，材料密度為7 850 kg/m3，彈性模量為2.06×1011N/m2。同時考慮靜載、桿件質量和螺栓球質量對組集質量矩陣[22]的貢獻。經模態分析[23]后得到前30階模態頻率，如表1所示。

表1 網架結構前30階自振頻率

2.2 沖擊力時程與加速度幅值

鑒于各節點豎向剛度的變化范圍為4.082 9× 107～1.4158×108kN/m，差異不大。不妨以具有適中剛度的159號節點(圖2中實心圓所示位置)作為重物懸掛點(即激勵點)。網架結構在懸掛點位置的豎向剛度為k1=8.166×107N/m(對應圖1所示振動系統的彈簧1剛度)。假設繩索的彈性模量為E=1.0×1011N/m2，截面面積為A2=78.5 mm2，繩索張緊長度為1.0 m(等于重物抬高高度s1)，繩索質量密度為7 850 kg/m3，重物質量為3 kg，振動系統的阻尼比為ζ=0.05，則張緊后的繩索剛度為k2=7.85×106N/m(對應圖1所示振動系統的彈簧2剛度)。不妨取γ=1.0。將這些參數帶入式(18)計算沖擊力時程，并將計算結果繪于圖3。不難發現，沖擊力的幅值很大，高達19.7 kN，但作用時間非常短，僅有1.04 ms。

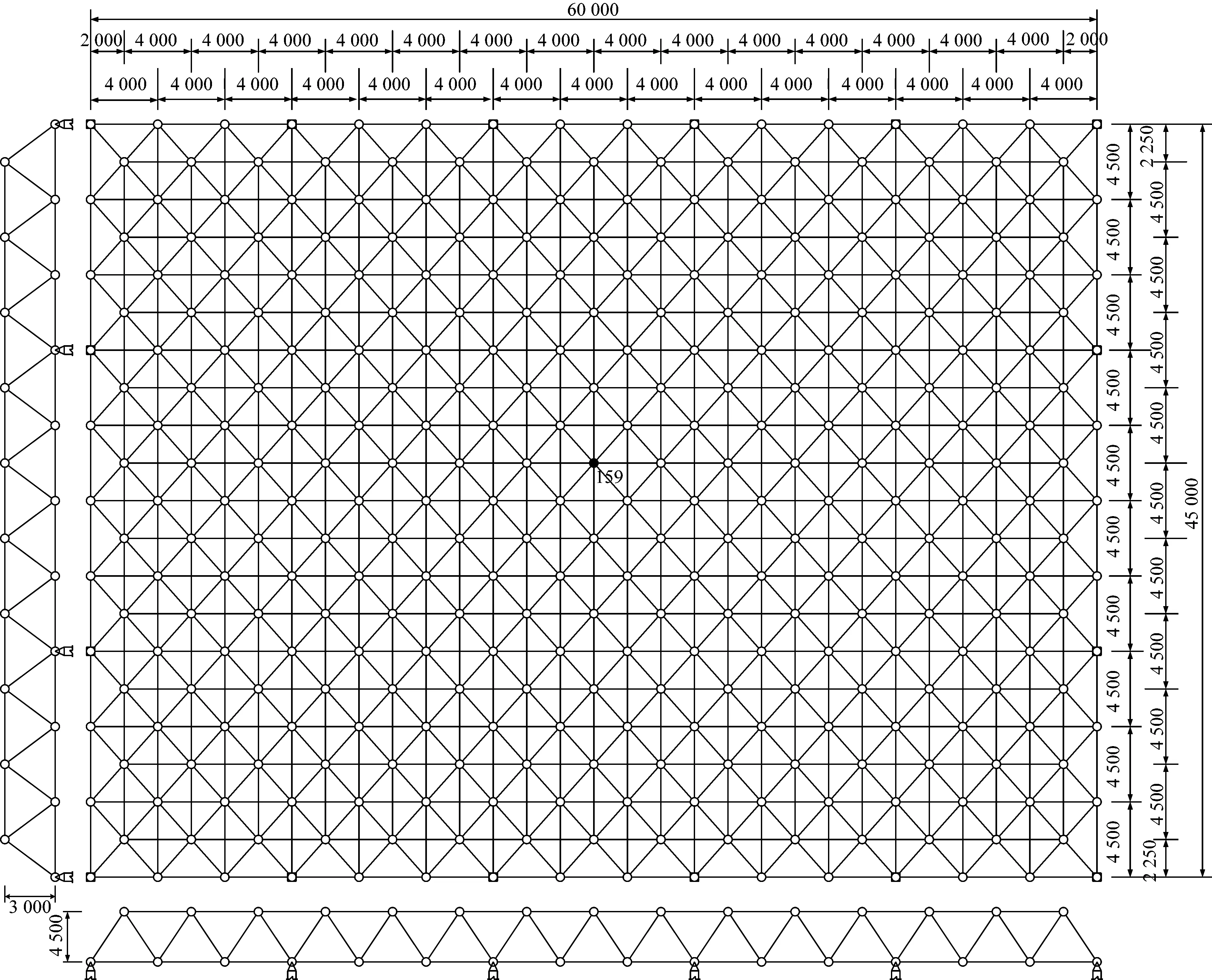
圖2 某60 m×45 m平板網架(mm)

在159z自由度(對應159號結點z向)施加圖3所示的沖擊力時程，并采用Newmark-β法計算響應時程。假設網架結構各階模態的阻尼比均為0.02，采樣頻率為50 kHz，采樣時長 0.5 s。最大加速度幅值為4.82 m/s2，所在位置與激勵點相同，對應的加速度時程如圖4所示。而第二大加速度幅值為1.51 m/s2，可見單點沖擊激勵可使激勵點處的加速度幅值遠高于其他自由度。

在159z自由度施加階躍激勵，最大加速度幅值同樣出現在該自由度。為了與沖擊激勵產生相同的最大加速度幅值，階躍激勵需要的重物質量為 368 kg，約為沖擊激勵所需重物質量的123倍。比較圖4、圖5可知，兩條加速度時程曲線的相位角相差π/2。

2.3 參數分析

根據式(16)、式(17)可知，重物質量、墜落高度、繩索彈性模量、繩索截面積和等效振動系統的阻尼比是影響沖擊力時程，進而影響最大加速度幅值的主要參數。應當考察這些參數對最大加速度幅值的影響。

假設繩索的彈性模量為E=1.0×1011N/m2，繩索截面積為A2=100 mm2，阻尼比為ζ=0.05。在1～10 kg內變化重物質量M，并取墜落高度s1變化范圍為0.5～3.0 m。將不同參數組合下計算得到的沖擊力時程施加于結構，并拾取結構的最大加速度幅值繪于圖6。不難發現，對于不同的墜落高度，最大加速度幅值與重物質量基本呈線性關系。重物質量越大，最大加速度幅值也越大。同時，墜落高度越大，直線的斜率越大。

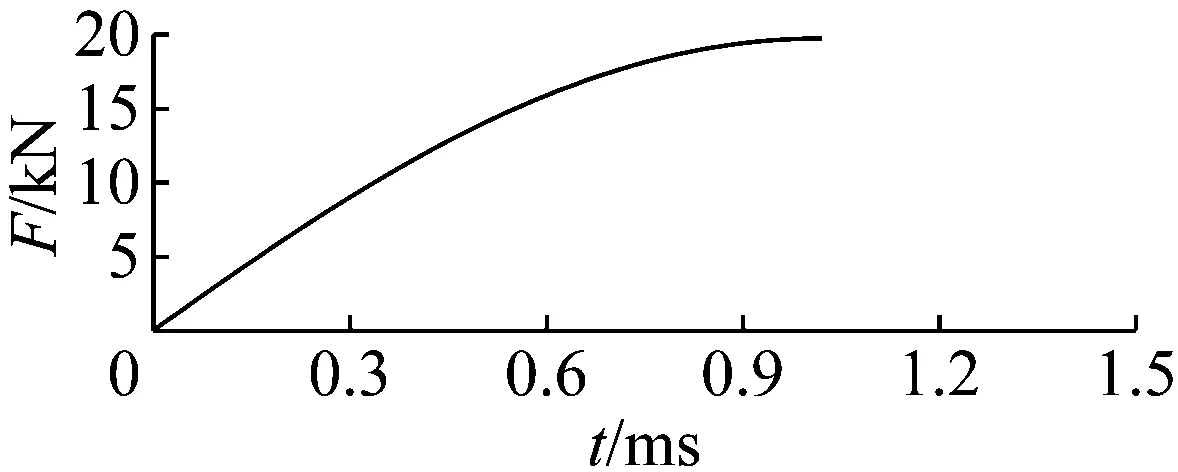
圖3 沖擊力時程

圖4 沖擊激勵下最大加速度幅值對應的自由度加速度時程

圖5 階躍激勵下最大加速度幅值對應的自由度加速度時程

假設重物質量為M=5 kg，墜落高度為s1=2 m，阻尼比為ζ=0.05。在0.25×1011～2.00×1011N/m2內變化繩索彈性模量E，并取繩索截面積A2變化范圍為50～300 mm2。將不同參數組合下計算得到的沖擊力時程施加于結構，并拾取結構的最大加速度幅值繪于圖7。由圖7可知，對于不同的繩索截面積，最大加速度幅值與繩索彈性模量的關系曲線均具有一定波動性，且變化非常平緩。可見，最大加速度幅值對繩索彈性模量的變化并不敏感。相比之下，當其他參數固定時，繩索截面積越大，最大加速度幅值也越大。

假設重物質量為M=5 kg，繩索彈性模量為E=1.00×1011N/m2，繩索截面積為A2=100 mm2。在0.01～0.10內變化等效振動系統的阻尼比ζ，并取墜落高度s1變化范圍為0.5～3.0 m。將不同參數組合下計算得到的沖擊力時程施加于結構，并拾取結構的最大加速度幅值繪于圖8。由圖8可知，對于不同的墜落高度，最大加速度幅值大致隨阻尼比的增大而減小，但變化較為緩慢。可見，最大加速度幅值對阻尼比的變化并不敏感。當其他參數固定時，墜落高度越大，最大加速度幅值也越大。

從圖6～圖8綜合判斷，結構的最大加速度幅值對重物質量、墜落高度和繩索截面積較為敏感，對繩索彈性模量和等效振動系統的阻尼比不敏感。因此，較大的重物質量、墜落高度和繩索截面積有利于結構產生較大的加速度幅值。

根據杜哈梅積分，結構的加速度響應由結構動力特性和沖擊力時程共同決定。由于算例中結構動力特性是固定的，各節點豎向剛度(即k1)差異不大(變化范圍為4.082 9× 107～1.415 8×108kN/m)，而其他所考察參數的變化范圍較大，因此可以定性判斷，即使選取其他節點作為激勵點，算例中結構最大加速度幅值對各參數的敏感性也不會有太大變化。

但是，若以其他結構(如不同類型和不同跨度的網架、網殼等)作為分析對象，則由于動力特性不同以及各節點豎向剛度可能存在較大差異，結構最大加速度幅值對各參數的敏感性值得進一步考察。

圖6 重物質量和墜落高度對最大加速度幅值的影響

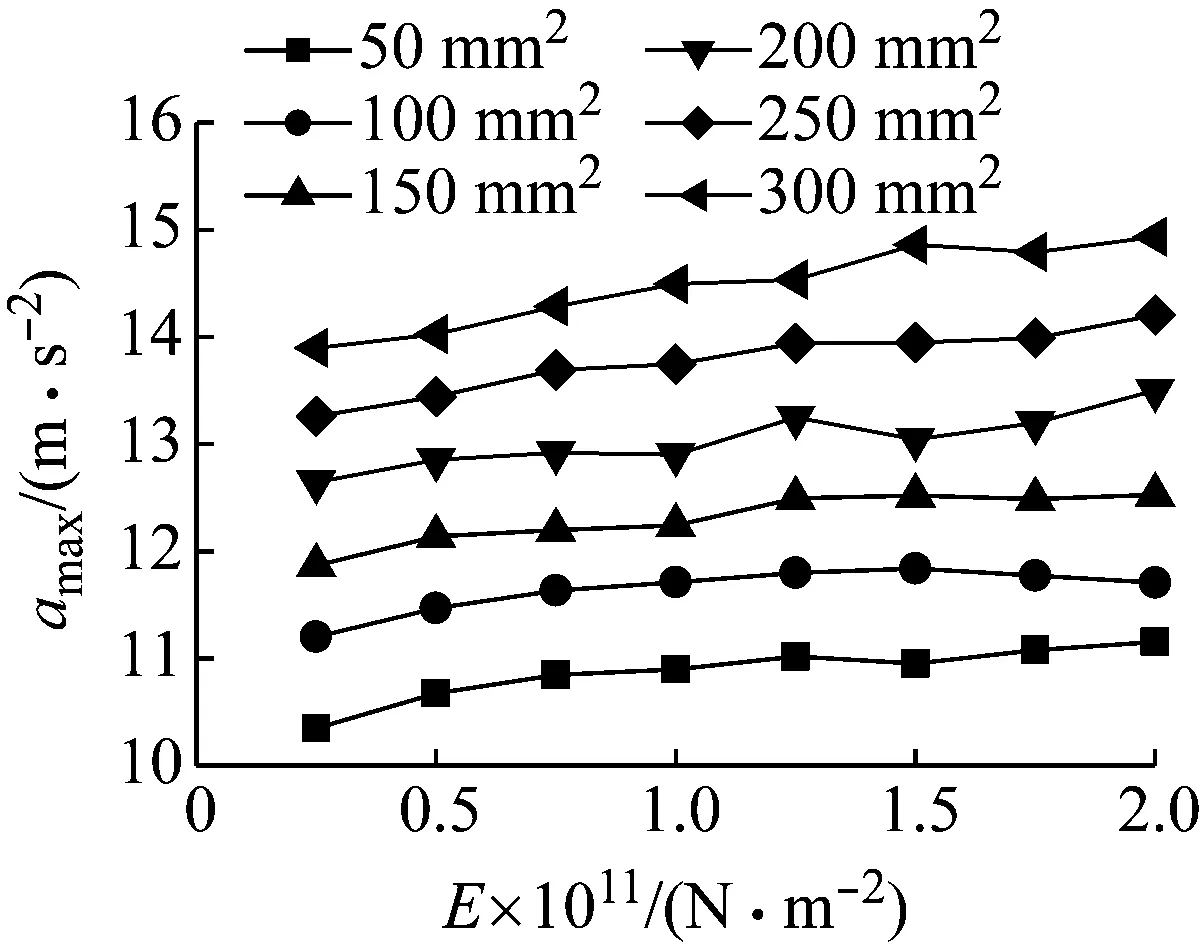
圖7 繩索彈性模量和截面積對最大加速度幅值的影響

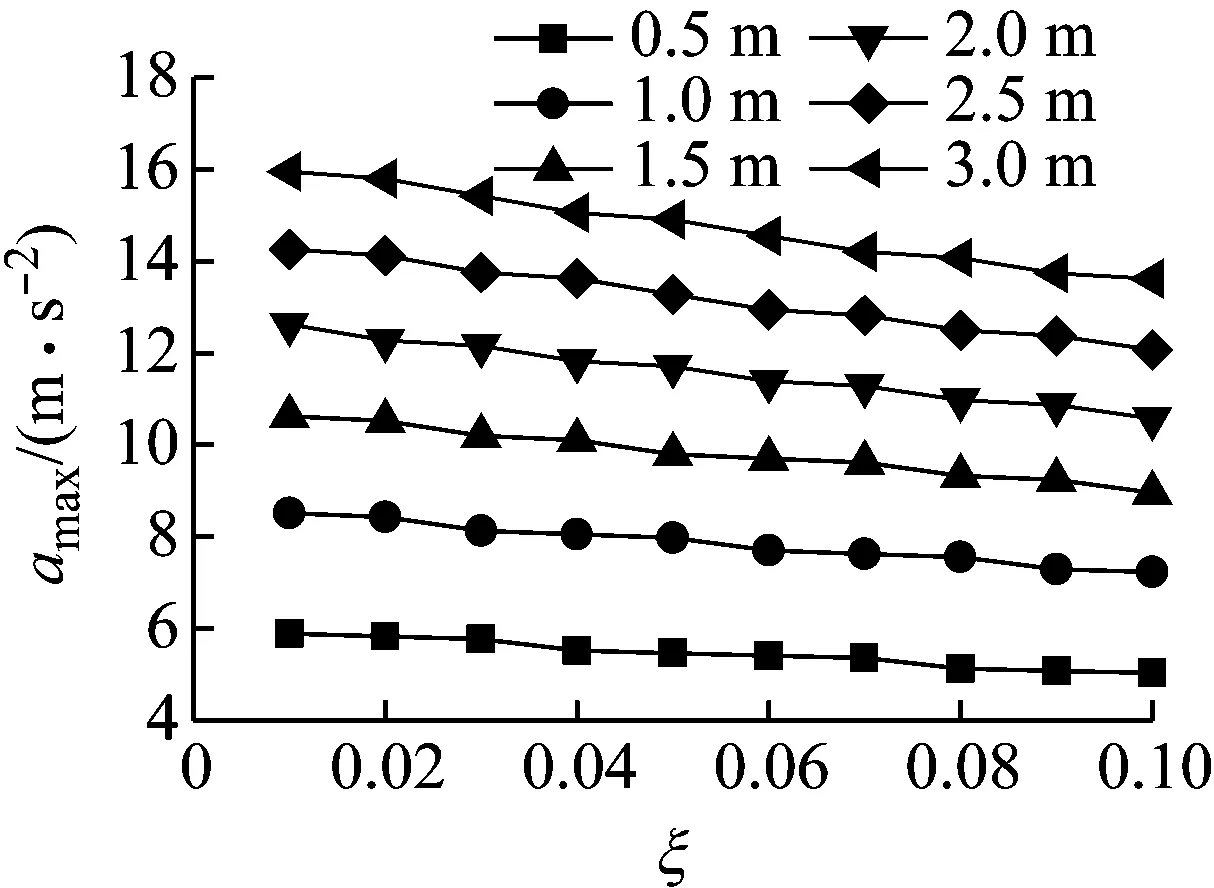
圖8 等效振動系統阻尼比對最大加速度幅值的影響

2.4 與階躍激勵的比較

假設繩索的彈性模量為E=1.0×1011N/m2、繩索截面積為A2=100 mm2、等效振動系統的阻尼比為ζ=0.05。在1～10 kg內變化重物質量M，并取墜落高度s1變化范圍為0.5～3.0 m。將不同參數組合下計算得到的沖擊力時程施加于結構，并拾取結構的最大加速度幅值列于表2。表2中還列出了階躍激勵產生相同最大加速度幅值所需的重物質量。以表3中第1行第1列數據(1.22, 93)為例來說明表中數據的含義。該數據表示當重物質量為1 kg、墜落高度為0.5 m時，沖擊激勵產生的最大加速度幅值為1.22 m/s2，階躍激勵產生相同最大加速度幅值所需的重物質量為93 kg。由表2可知，為了產生相同的最大加速度幅值，階躍激勵所需的重物質量遠高于沖擊激勵(表2中介于83.2倍～356.0倍)。

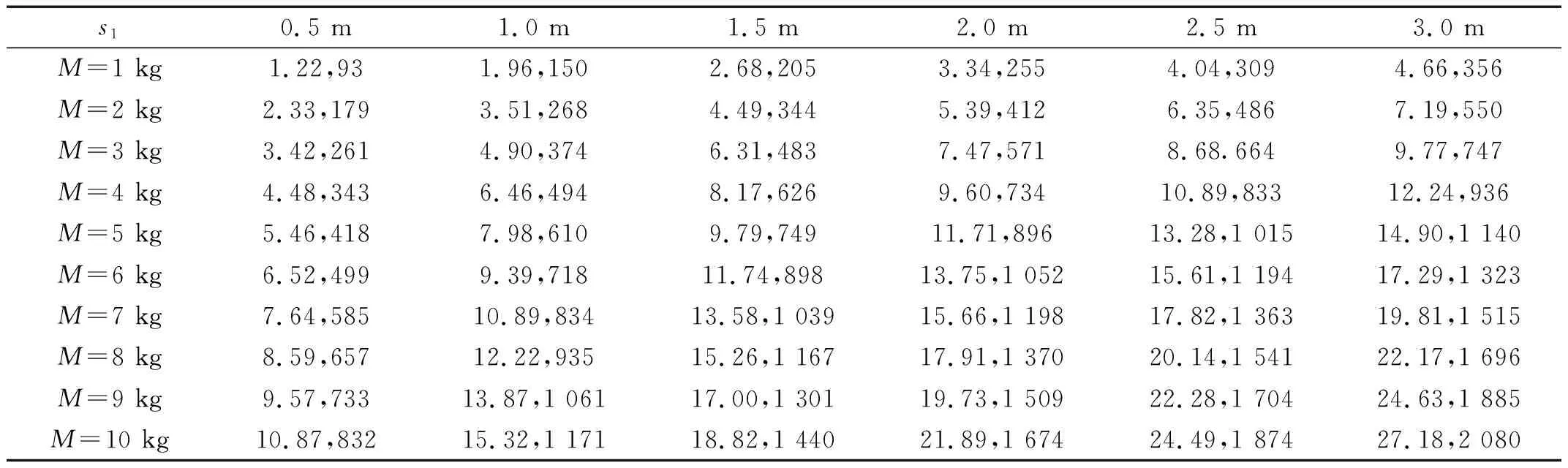
表2 沖擊激勵與階躍激勵所需重物質量的比較

3 結 論

以網架結構為例，提出一種基于重物墜落的沖擊激勵新方法。算例表明，所分析的網架結構最大加速度幅值對重物質量、墜落高度和繩索截面積較為敏感，對繩索彈性模量和等效振動系統阻尼比不敏感。與階躍激勵相比，沖擊激勵所需的重物質量大為減少，這有利于提高網架結構的動力測試效率、降低測試成本和獲得具有較大信噪比的響應信號。本文工作為網架結構的主動激勵提供了一種新的思路。在實際應用中，可以對等效振動系統的數學模型進行參數修正以考慮建模誤差的影響。