仿雁群陣列量子空中通信組網構建策略*

姚明輝 聶敏 楊光 張美玲 孫愛晶 裴昌幸

1) (西安郵電大學通信與信息工程學院,西安 710121)

2) (西安電子科技大學,綜合業務網國家重點實驗室,西安 710071)

量子衛星通信是量子通信領域的研究熱點和前沿,具有覆蓋面廣、通信效率高和安全性強的特點.量子通信組網的構建策略是量子通信的重要組成部分,然而,有關量子空中通信組網構建策略的研究,迄今尚未展開.本文采用仿生學原理,根據雁群空中飛行陣列的特點,提出了一種仿雁群Λ 型量子空中通信組網拓撲結構,該結構可分為單頭節點Λ 型和多頭節點Λ 型.基于Greenberger-Horne-Zeilinger (GHZ)態的可認證QSDC網間通信系統和GHZ-EPR (Einstein-Podolsky-Rosen)量子衛星組網隱形傳態通信系統,對該Λ 型量子空中通信組網結構的誤碼率、能耗、吞吐率等參數進行了研究.理論分析和仿真結果表明,仿雁群單頭節點Λ 型組網結構,在噪聲平均功率譜密度為2 dB/m 的環境中,當網中頭節點與子節點的通信距離小于400 m 時,誤碼率小于0.094;若頭節點與子節點的通信距離由400 m 增大到1000 m 時,誤碼率增長較快,達到0.585;當單側子節點數由2 增加到7 時,吞吐率由110.6 kb/s 下降到46.45 kb/s.以總節點數21 為例,單頭節點Λ 型組網結構可節省32.6%的能量,吞吐率下降到23.9 kb/s.相比之下,總節點數為21 的多頭節點Λ 型組網結構,可節省29.3%的能量,吞吐率達到163.4 kb/s.由此可見,采用仿雁群陣列結構的量子空中組網,具有很好的網絡可擴展性、優良的信息安全性和靈活的網絡結構.

1 引言

量子通信和量子信息處理,是目前國內外的研究熱點和前沿.我國“十四五”規劃中,將量子通信和量子計算列為國家的重要發展戰略.近些年,量子通信領域取得了許多優秀的研究成果.潘建偉院士團隊[1,2]于2018 年實現了冷原子系統內單集體激發態的相干操縱;又于2019 年提出了無需量子存儲器的實驗量子中繼器,通過操縱12 光子干涉儀,將量子糾纏的產生率提高了89%.在此基礎上,該團隊于2020 年成功構建了76 個光子的量子計算原型機“九章”;在發展了量子光源受激放大的理論和實驗方法后,又構建了113 個光子144 模式的量子計算原型機“九章二號”,實現了相位可編程功能.郭光燦院士團隊[3,4]于2020 年實現了對高維量子態的直接強測量;2021 年在高阻抗微波諧振腔內,完成了兩個半導體量子比特間的長程耦合,提出了一種新型譜學方法,更快速、更直觀地表征了量子比特間的耦合關系.2000 年,龍桂魯教授團隊[5]提出了量子安全直接通信(quantum secure direct communication,QSDC)方案,這是一種高安全性的通信模式.之后,龍桂魯教授團隊對QSDC 進行了更深入的研究,取得了一系列突破性成果.2020 年,龍桂魯教授團隊[6]提出了第一個與設備無關的量子安全直接通信方案;2021 年,龍桂魯教授團隊[7]又使用掩蓋編碼技術,大幅度增大了量子直接通信的系統容量.

近年來,國際上有關量子通信的研究,也取得了一系列突破性成果.2016 年,美國約翰斯霍普金斯大學量子物質研究所物理與天文學系Pan 等[8]對量子自旋冰Yb2Ti2O7結構特性進行了研究,發現磁化率的形式與單極氣體的形式一致,且可以定義和測量磁單極電導率.2020 年,佛羅里達州國家高磁場實驗室Pan 等[9]研究了增強射頻輻射下量子斯格明子霍爾效應(Hall skyrmions)的穩定性,并討論了這種穩定性的可能來源.2021 年,德國帕德博恩大學光子量子系統研究所J?ns 團隊[10]進行了量子芯片層面的研究,通過實驗論證了集成光子學與量子技術相結合的可行性,為下一代集成電路的研發開拓了新的思路.2021 年,德國馬克斯普朗克科學研究所Henke 等[11]搭建了一個用于探索自由電子的量子光學通用平臺,實現了集成光子學連續束電子相位調制.

2016 年8 月16 日,中國在酒泉衛星發射中心,成功發射了世界上第一顆量子科學實驗衛星“墨子號”[12];2017 年中國在國際上首次實現了千公里級的星地雙向量子通信[13];同年9 月,世界首條量子保密通信干線—“京滬干線”正式開通.結合“京滬干線”與“墨子號”量子衛星的天地鏈路,中國首次實現洲際量子保密通信[14];2021 年,在“京滬干線”與“墨子號”對接的基礎上,中國成功組建天地一體化量子通信網絡[15],這些成果標志著中國構建量子通信天地一體化廣域網的技術逐漸成熟.

空中通信組網的構建,是當前國防、民用航空、無人機通信等領域的研究前沿[16?20].但是,迄今為止,國內外對于空中通信組網的研究,僅局限于經典通信領域.對于雁群空中飛行陣列,研究者們取得了一些原創性成果,并被應用于仿生學領域[21?24].然而,仿雁群陣列量子空中組網構建策略的研究,迄今尚未展開.受到雁群空中飛行陣列的啟發,本文將其與量子衛星通信相結合,提出了一種仿雁群 Λ 型量子空中組網拓撲結構,構建了相應通信系統.通過仿真分析誤碼率、吞吐率和能耗等參數,研究了該組網結構的各項性能.希望通過本文,為量子空中通信組網的研究提供新的思路.

2 仿雁群Λ 型陣列量子空中組網結構特點

2.1 雁群空中飛行陣列特點

大雁在遷徙過程中,飛行陣列如圖1 所示,本文稱之為“ Λ 型”飛行結構.在 Λ 型陣列中,頭雁帶領隊伍飛行.鳥類行為學研究表明[24],大雁在飛行過程中,自身不斷地拍打翅膀,產生上升渦流.利用這種渦流,尾隨的大雁在飛行過程中會減少自身能量的消耗,每只尾隨的大雁均會獲得其前方大雁產生的渦流幫助,但頭雁沒有渦流可用,所以相對于雁群中的其他大雁會消耗更多的能量.在長途遷徙過程中,頭雁和尾雁周期性地交換位置,以此來節省飛行的能耗.相關研究表明,Λ 型陣列飛行的大雁,比獨自飛行的大雁節省70%的能量[25].

圖1 雁群飛行陣列Fig.1.Geese flying array.

2.2 仿雁群量子空中組網

根據雁群飛行陣列,提出仿雁群Λ 型量子空中組網(simulated wild goose group Λ-type quantum air networking,SWGGΛ-TQAN),將組網中的各個成員以節點方式呈現,SWGG Λ -TQAN 由量子衛星(quantum satellite)、頭節點(head node)和子節點(child node)組成.單頭節點SWGGΛTQAN 的構建如圖2 所示.

圖2 單頭節點SWGGΛ-TQANFig.2.Single-head node SWGGΛ-TQAN.

對于單頭節點SWGG Λ -TQAN,需要考慮當子節點增多時,若無限制的向兩邊延伸,會使整個拓撲結構變得冗余,且單頭節點SWGG Λ -TQAN通信模型存在嚴重的安全隱患,即若頭節點發生故障,該組網中所有子節點也會故障.以總節點數目21 為例,單頭節點SWGGΛ-TQAN 模型如圖3所示.

圖3 單頭節點SWGGΛ-TQAN(總節點數目21)Fig.3.Single-head node SWGGΛ-TQAN (total number of nodes of 21).

基于上述分析可知,單頭節點SWGGΛ-TQAN不適用于總節點數目過多的情況,因此提出多頭節點SWGGΛ-TQAN,組網結構如圖4 所示.

多頭節點SWGGΛ-TQAN 相較于單頭節點SWGGΛ-TQAN,結構不再單調,且多個頭節點的引入可以保證網絡不會輕易陷入癱瘓.多頭節點SWGGΛ-TQAN 實質上是由多個單頭節點SWG GΛ-TQAN 組成,可根據不同的總節點數目,建立相應的組網結構,尤其是在總節點數目過多的情況下,比單頭節點SWGGΛ-TQAN 表現的更加出色.圖4 僅為示意圖,每個單頭節點SWGGΛ-TQAN的節點數量應根據具體情況及后續分析結合決定.為了便于對比,提出21 節點下的多頭節點SWGGΛTQAN,如圖5 所示.

21 節點下的多頭節點SWGGΛ-TQAN 模型中共有3 個單頭節點SWGGΛ-TQAN,假設頭節點1 所在自身組網為A,頭節點2 所在自身組網為B,頭節點3 所在自身組網為C,A 中共有11 個節點,B 中共有7 個節點,C 中共有3 個節點.正常情況下各頭節點會進行通信,除頭節點間相互通信外,不會進行與其他組網的任何通信.以B 為例,如果頭節點2 故障,頭節點1 與頭節點3 在與頭節點2 通信時發現異常情況,根據最短通信距離和子節點數目不宜過多原則,頭節點3 建立與B 內其余節點的通信.即當某一頭節點發生故障,與之通信的相鄰組網頭節點在發現問題后,可建立與該組網子節點的通信,確保其余節點不會進入失控狀態.以A 中的Ex1 節點為例,如果該子節點故障,組網頭節點1 發現異常情況,通過頭節點間的通信告知相鄰頭節點2 異常情況,頭節點2 收到異常情況后告知頭節點3,頭節點2 與A 中脫節的子節點建立通信.即當某一組網中子節點發生故障,該組網頭節點發現問題后,告知相鄰組網的頭節點,可通過位置調整等方法回到自身所在原組網,或在新組網中繼續通信,以確保被影響的子節點盡快恢復通信狀態.

SWGGΛ-TQAN 的單頭節點與多頭節點結構適用于多種空中組網情況,擁有可擴展性強、保密性高、通信效率高等優點,為量子空中通信組網的研究提供了新的思路.

2.3 SWGGΛ-TQAN 抗毀度定量分析

抗毀度是指網絡遇到確定性或隨機性故障時,網絡維持或恢復一個可接受程度的能力.對于單頭節點SWGGΛ-TQAN 通信系統,其抗毀度較差,某一子節點故障,會導致后續子節點的通信均故障,而頭節點的故障會導致整個組網通信系統的故障.

根據相關研究[26,27],將多頭節點的SWGGΛTQAN 抗毀度定義為網絡效率E的變化量,具體計算公式為

其中E1和E2分別表示節點故障前和節點故障后組網的網絡效率,ΔE的值越小,表示網絡的性能下降越少,抗毀度就越高[27].其中,SWGG Λ -TQAN網絡效率E為

式中N表示網絡中的節點個數;εij(D)1/dij(D),其中dij(D)表示頭節點i與子節點j的通信距離,路徑唯一,D表示兩節點間的實際距離.

由上述分析過程,以圖5 的21 節點SWGGΛTQAN 為例,可計算出E1的值.若此時故障的節點為頭節點2,結合2.2 節分析,可算出此時多頭節點SWGGΛ-TQAN 結構E2的值,則此時網絡的抗毀度為

若此時故障的節點為子節點Ex1,結合2.2 節分析,可得到此時多頭節點SWGGΛ-TQAN 結構的E2的值,此時網絡的抗毀度為

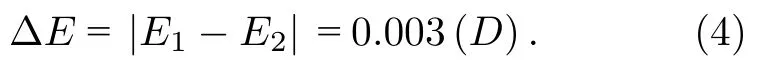
從計算過程可以發現,對于多頭節點SWGGΛTQAN,當有其他節點故障時,不管故障的節點是頭節點還是子節點,只要組網中仍存在正常通信的頭節點,整個組網依然可以保持通信.計算結果和分析表明,多頭節點SWGGΛ-TQAN 具有良好的抗毀性.

3 SWGGΛ-TQAN 通信系統構建

3.1 GHZ-EPR 量子衛星-組網隱形傳態通信系統

整個網絡通信的構建分為衛星與網絡和網絡與網絡兩部分,衛星與網絡的通信是由衛星與頭節點構成的,網間的通信是各節點間構成的.本文將采用量子隱形傳態(quantum teleportation,QT)技術來構建衛星與網絡的通信,使用QSDC 技術來構建網間通信.

量子物理系統會隨著糾纏粒子數量的增加,提供更大的存儲空間和更強大的并行能力,因此研究者們一直都希望使用更多的糾纏粒子來進行信息處理.量子糾纏交換基于沒有直接相互作用的糾纏粒子上測量實現[28],EPR 對是兩個量子態糾纏,Greenberger-Horne-Zeilinger (GHZ)態 是3個量子糾纏.糾纏量子比特經常會被用到遠程態制備、量子秘鑰分發等技術的量子信道中,量子信道相比于經典信道具有更高的安全性.劉乾和胡占寧[29]對理論知識進行相關分析,本文在完善分析的同時,進行了通信系統的構建及通信過程的敘述.

GHZ 態是一種經典不可分的三量子比特糾纏態,也是一種最大糾纏態粒子,GHZ 型量子糾纏是一種量子疊加系統,包含3 個量子比特.8 種GHZ態粒子如下所示:

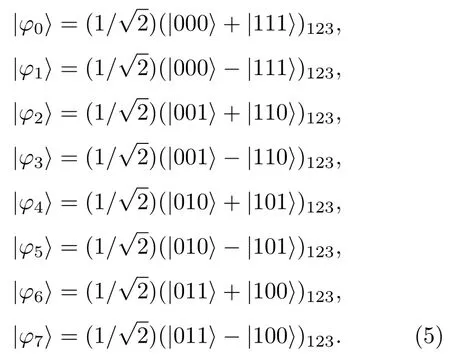
在該通信系統中,通信雙方均具有3 個量子位粒子和一對Einstein-Podolsky-Rosen (EPR)糾纏態,將本地和遠程粒子構成兩個GHZ 態粒子,構成的GHZ 態粒子將被用于量子信道.為了便于對通信系統進行說明,假設衛星為通信方Alice,頭節點為通信方Bob,則整個通信系統如圖6 所示.

圖6 GHZ-EPR 混合隱形傳態系統Fig.6.GHZ-EPR hybrid teleportation system.

該粒子狀態進行糾纏變換后得到

通信系統的通信過程如下.

步驟1通信雙方Alice 和Bob 按照圖6 所示制備GHZ 態粒子和EPR 糾纏對,進行通信前的準備.通信系統中A1B1B2形成一個GHZ 態粒子,A2A3B3形成另外一個GHZ 態粒子,兩個GHZ 態粒子與兩個EPR 糾纏對共同構成了該通信系統.

步驟2Alice 和Bob 進行CNOT 操作,該過程中p1和q1作為控制量子比特,A1和B3作為目標量子比特.

步驟3通信雙方Alice 與Bob 對A1,B3,p1和q1進行量子測量,測量方式為Alice 在自己側對A1進行Z 基測量,對p1進行X 基測量,Bob 在自己側對B3進行Z 基測量,對q1進行X 基測量.各自測量結束后,剩余未被進行測量粒子B1,B2,A2,A3,p2,q2狀態崩塌,通信雙方Alice 和Bob 用經典信道相互通知對方測量結果.

步驟4在分別接收到對方發送的p1和q1的測量結果后,Alice 和Bob分別在p2和q2上進行X 基測量.

步驟5Alice 和Bob 執行酉操作來進行狀態準備,根據各自在p2和q2上得到的測量結果,分別對A2,A3,B1和B2進行幺正變換,之后Alice 對EPR 狀態進行重構,Bob 對EPR 狀態進行恢復.

最終得到的結果:p1和p2的初始狀態表示形式處于B1和B2上,而q1和q2的初始狀態表示形式在A2和A3上.

對于上述第5 步的操作,假設在第3 步結束時,系統中剩余粒子組成的崩塌狀態為

在計算雙向量子隱形傳態的效率時,Shima和Monireh 等[30]利用量子信道的傳輸態,將協議的效率定義為ηc/qc,式中c表示量子通道傳送的量子態數,qc表示用于構造量子通道的量子位.將本方案與一些典型的雙向量子隱形傳態的效率對比,如表1 所列,可觀察到具備良好的通信效率.

表1 雙向量子隱形傳態協議對比Table 1.Comparison of two-way quantum teleportation protocols.

3.2 基于GHZ 態的可認證QSDC 網間通信系統

QSDC 可以在量子信道中直接安全的傳輸經典信息,且通信過程不需要密鑰的生成,無需分配資源進行密鑰的管理,也無需后續的加密和解密過程.雖然其發展起步較晚,但是在20 多年的發展歷程中,衍生出了許多通信協議,在2021 年9 月30 日,量子安全直接通信首次實現了15 個用戶間的通信,傳輸距離可以達到40 km[34].QSDC 作為量子領域的研究熱點,也產生了許多通信協議[35?38],而王明宇等[39]提出的量子直接傳態使QSDC 應用到量子態的信息傳輸.

SWGG Λ -TQAN 使用QSDC 進行通信時,要考慮竊聽和入侵節點等安全問題.使用基于GHZ態的可認證QSDC 協議進行網間通信,通信雙方可以確認對方的安全性后進行通信.為了便于對協議進行敘述,將通信雙方定義為Alice 和Bob,在通信開始前,Alice 和Bob 需要共享長度為n的密鑰q序列,便于后續雙方的身份認證.

步驟1Alice 根據自己需要傳輸的信息M制備一串單光子序列和一串GHZ 態序列.GHZ 態序列中每個粒子為(5)式中的一種狀態,每個單光子為|0〉,|1〉,|+〉,|?〉四種狀態之一,其中(|0〉,|1〉)是一組標準正交基,稱為Z 基,(|+〉,|?〉)是一組標準正交基,稱為X 基.X 基與Z 基為非正交基,且具有如下變換關系:

步驟2Alice 將GHZ 態序列中的粒子分別抽出構成序列S1,S2和S3,隨后Alice 根據密鑰q序列對序列S1按照如下規則操作:

q10時,在S1序列中找到第1 個|+〉,記錄其位置L1,之后當q11時,在S1序列中找到第1 個|1〉,記錄器位置L1;

q20時,在序列S1中位于L1位置處之后的粒子中,找到第1 個|+〉,將該位置標記為L2;q21時,采取相同操作將L1后的第1 個|1〉的位置標記為L2.根據上述操作,標記完所有序列,得到位置序列L(L1,L2,···,Ln) .

步驟3Alice 在序列S1中隨機加入單光子序列得到,將序列發送給Bob,在確認到Bob 接收到序列后,公布檢測粒子的位置與測量基.Bob 根據Alice 公布的信息對序列進行Z 基或X 基測量,并將測量后的結果等信息返還給Alice,Alice 拿到這些信息后,根據計算結果的錯誤率判斷該通信信道是否安全.若不安全則放棄此次通信,若信道安全則進行下一步.

步驟4Alice 與Bob 進行身份認證.Alice 通過無法被修改的經典信道將位置序列L公布給Bob,Bob 使用最開始制備的密鑰選擇對應的測量基進行測量.對應位置Li使用qi測量,并得到最終的測量結果q′.如果序列q′q,則身份認證成功,節點并未發生異常,不相等則說明存在異常,此時放棄通信.

步驟5在驗證完信道與通信節點的安全性后,Alice 將序列S2和單光子序列結合得到序列,將序列發送給Bob.

步驟6Bob 拿到序列后,Alice 公布對應單光子序列位置和測量基信息,Bob 根據Alice 的信息對序列測量,根據測量結果分析是否可繼續通信.

步驟7同第5 步,Alice 將S3序列和單光子序列結合得到序列,并將序列發送給Bob.

步驟8Bob 接收到序列后,Alice 公布對應單光子序列位置和測量基信息,Bob 根據Alice 的信息對序列測量,分析錯誤率,如同第6 步.

步驟9整個通信過程均無問題后,Alice 將原序列所有需要的信息均發送給Bob,Bob 根據Alice 發送的消息對序列進行恢復和測量.最終得到Alice 需要傳輸的信息M.

在該協議中,定義(5)式中的8 種GHZ 態粒子形式分別對應000—111 八種編碼.假設Alice要發送編碼信息001,則在通信開始前,需要制備的GHZ態粒子為|φ2〉同時假設用到的單光子為|?〉和|+〉.則Alice 抽出每列粒子構成的序列S1,S2和S3分別為

進行位置標記后,假設Alice 選取|?〉隨機加入S1序列構成序列,并發送給Bob,Bob 同時進行信道安全性測量和身份認證.由(10)式和(11)式可得出序列為

信道確認安全且身份認證通過后,假設Alice 選取|+〉隨機加入S2序列構成序列,發送給Bob,Bob 接收到序列后,再進行一次安全驗證.由(10)式和(11)式可得出序列為

信道沒有安全問題時,Alice 發送S3序列,假設Alice 選取|?〉隨機加入S3序列構成序列,則序列為

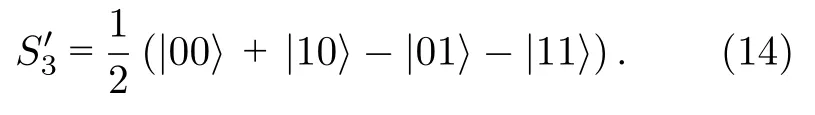
Bob 接收到序列后告知Alice,Alice 確認無誤后,將原序列中位置等信息經過無法修改的信道傳遞給Bob,Bob 對序列進行恢復,最終得到Alice想要發送的編碼信息001.

該通信協議使用GHZ 態粒子,給信道提供更高的通信容量,一個量子態可以存儲4 bit 的信息量.使用QSDC 技術后,雖然該通信協議涉及到了密鑰的使用,增加了資源的消耗,但是可以有效抵御第三方的截獲攻擊或重發攻擊,輔助粒子攻擊等多種攻擊方式.即使在通信過程中,某一通信節點發生異常,通信協議中的身份認證功能可以有效防止該異常節點對SWGGΛ-TQAN 造成進一步的破壞.

量子通信協議的效率是根據量子通信效率和量子比特效率衡量的,量子傳輸效率[40]定義為

式中ms表示通信過程中傳輸的信息總量,qu表示通信過程中的總量子比特數,pc表示通信過程中的總經典比特數.量子比特效率[40]定義為

式中qc為通信過程使用到的量子比特.網間通信系統中,為了建立安全的通信信道,使用了nM個量子比特作為密鑰序列,完成身份認證功能.當需要傳輸 8M個總信息比特時,使用到的總量子比特數為 4M個,使用到的經典比特數為 3M個,故該通信系統的量子傳輸效率為

量子比特效率為

將經典的QSDC 方案與網間通信系統方案進行量子傳輸效率、量子比特效率和編碼容量對比分析,結果如表2 所列.可以看出該網間通信系統的量子比特率并列最高,且由于GHZ 態粒子的使用,在保證了高編碼容量的同時具備良好的傳輸效率.

表2 QSDC 協議參數比較Table 2.Comparison of QSDC protocol parameters.

4 性能仿真分析

4.1 SWGGΛ-TQAN 傳輸誤碼率分析

在實際應用中,環境噪聲、人為干擾等因素都會影響通信性能,產生通信問題.針對SWGGΛTQAN,設量子信息傳輸誤碼率為Pr[43],則在本文中網間誤碼率Pr的計算公式為

式中,σ表示噪聲平均功率譜密度,n表示頭節點的個數,nL表示對應傳輸距離的子節點個數,L表示網間信息傳輸距離,λ為光子波長,fT表示發送端孔徑,fR表示接收端孔徑,FT表示發射端傳輸因子,FR表示接收端傳輸因子,Lp鏈路損耗.

根據相關分析[44],當選擇λ=1550 nm 的光波長時,可以削減自然大氣環境對傳輸鏈路的衰減.分析單組網情況 (n1) 誤碼率Pr和網間信息傳輸距離L間的關系,在傳輸距離為L時,有2 個子節點 (nL=2),誤碼率公式中的其他變量設置為fT=fR=35 mm,FT=FR=1,Lp=5%,噪聲平均功率譜密度σ2分別設置為1,2 和3 dB/m.

如圖7 所示,σ2一定時,頭節點與子節點的通信距離越遠,網間量子誤碼率越大.在σ2=1 dB/m 環境下,網間通信距離由300 m 增大到800 m 時,誤碼率由0.026 增大到0.187.當頭節點與子節點的通信距離固定時,隨著σ2增大,網間量子誤碼率也會增大.在頭節點與子節點的傳輸距離為700 m 條件下,σ2=1 dB/m 時,誤碼率為0.143;σ2=3 dB/m 時,誤碼率為0.43.

圖7 頭節點和子節點間通信距離與誤碼率的關系Fig.7.Relationship between bit error rate and communication distance between head node and child node.

除了上述趨勢,當網間通信距離在400 m 內,隨著通信距離的增大,誤碼率增長的幅度不大.以σ22dB/m 環境為例,當通信距離在0—400 m范圍內,誤碼率由0 增長到0.094,但當最遠通信距離大于400 m,由400 m 增大到1000 m 時,誤碼率由0.094 增大到0.585,σ21dB/m 與σ23 dB/m 環境下也是同樣的趨勢.綜上所述,若頭節點與子節點的通信范圍在0—400 m 內,誤碼率的提升緩慢;當通信距離大于400 m 時,誤碼率的提升較快,將400 m 定義為“網間敏感距離”.

對于單頭節點SWGGΛ-TQAN,增加子節點時,只能向兩側延伸,頭節點與處子節點的通信距離一旦超過“網間敏感距離”,誤碼率的較快增長會使網絡通信質量受到很大影響.對于多頭節點SWG GΛ-TQAN,即類似于圖4 的拓撲結構,總節點個數相同時,該結構會存在多個單頭節點SWGGΛTQAN,對于每一個單頭節點SWGGΛ-TQAN,頭節點與最遠子節點的通信距離超過“網間敏感距離”的可能性更低,此時誤碼率對網絡通信質量影響較小.

4.2 SWGGΛ-TQAN 能耗分析

SWGGΛ-TQAN 中每個節點的能耗均為兩部分,即飛行能耗和通信能耗,假設 SWGGΛ-TQAN存在N個節點,以持續時間T為一個周期.在該周期內,每個節點的運動情況分為移動或懸停.設懸停時的功率為Ps,移動時的功率為Pm,移動時的速度為v,由于速度加速至v或減速過程至 0 的時間極短,可忽略.設在T內有t1時間內節點在運動,則其位移能耗Em為

則節點在T內有T ?t1時間處于懸停狀態,節點的懸停能耗Es為

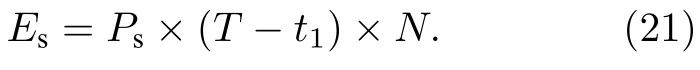
衛星與頭節點每次通信過程中,定義頭節點接收單位數據量功率為Pa;在網內通信中,定義節點需要接收或傳輸單位數據量的功率為Pb.頭節點需要完成與衛星及兩個子節點的通信,若頭節點數目為Nf,則頭節點的通信能耗Ef為

子節點每次通信均需要一次接收與一次傳輸,則總體子節點的通信能耗Ec表示為

因此,整個組網在時間T內的總能耗為

基于上述分析,給定懸停功率Ps為2 W,移動功率Pm為4 W,頭節點與衛星通信的數據功率Pa為5 W,網間通信功率Pb為3 W,每個持續時間T內均有80%的時間在運動,即t0.8T.

以21 節點為例,針對多頭節點SWGGΛ-TQAN、單頭節點SWGGΛ-TQAN 和節點不構成SWGGΛTQAN 這3 種結構,分析各自能耗.多頭節點SWG GΛ-TQAN 共有3 個頭節點,18 個子節點;單頭節點SWGGΛ-TQAN 有1 個頭節點和20 個子節點;不構成SWGGΛ-TQAN 時,節點間沒有聯系,為21 個頭節點.

圖8 是3 種結構隨時間的總能耗變化.顯然,3 種結構的能耗均隨時間增大,且無組網結構的總能耗遠大于SWGGΛ-TQAN 結構的總能耗.當T為4 h,無組網結構的總能量消耗為1226 J,單頭節點SWGGΛ-TQAN 的總能量消耗為826.4 J,多頭節點SWGGΛ-TQAN 的總能量消耗為866.4 J;當T為9 h,無組網結構的總能量消耗為2759 J,單頭節點SWGGΛ-TQAN 的總能量消耗為1859 J,多頭節點SWGGΛ-TQAN 的總能量消耗為1949 J.針對于單頭節點SWGGΛ-TQAN 和多節點SWGGΛTQAN,在相同總節點數的情況下,將一些子節點變為頭節點,多頭節點SWGGΛ-TQAN 的能耗更大是正常現象.但相同時間內增大的能耗不到5%,考慮到誤碼率等其他屬性的優勢,該能耗是可以被接受的.

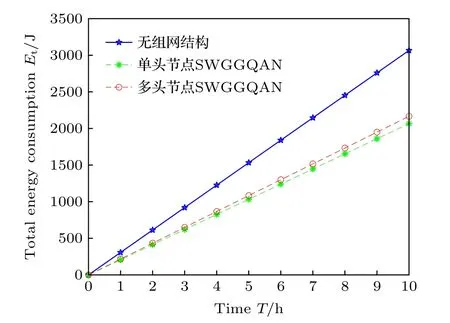
圖8 總能耗隨時間變化Fig.8.Variation of total energy consumption with time.

取上述參數時,單頭節點SWGGΛ-TQAN 相較于無組網結構的能量節省為32.6%,多頭節點SWGGΛ-TQAN 相較于無組網結構的能量節省為29.3%.考慮到實際自由空間中,公式中各參數值會比該仿真條件下參數值更大,可以預見到SWG GΛ-TQAN 在能量節省方面擁有優秀的性能,即具備雁群陣列的優勢.

4.3 SWGGΛ-TQAN 吞吐率分析

在SWGGΛ-TQAN 中,設成功制備GHZ 態序列和單光子序列的概率為P1,通信雙方認證成功的概率為P2,子節點成功收到量子信息的概率為P3,那么成功將一個量子態信息傳輸至第一個子節點的概率為

若SWGGΛ-TQAN 中每一側有Y個子節點,則對于某一側最后一個子節點,成功收到量子態信息的概率為

在頭節點與第一個子節點的通信過程中,制備GHZ 態序列和單光子序列的時間為C1,雙方進行身份認證的時間為C2,量子信息通過信道的傳輸時間為C3.因此,成功將信息傳輸至第1 個子節點的時間為

若SWGGΛ-TQAN 中每一側有Y個子節點,則對于某一側最后一個子節點,成功收到信息時需要的時間為

則對于SWGGΛ-TQAN,吞吐率可以定義為

考慮到節點間的通信與身份認證均在信道,以及在自由空間傳輸時不同因素的干擾,則C1和C2相比于C3很小,可以忽略不計,所以

根據文獻[45]可知,自由空間理想條件下的通信概率可以達到0.95,所以取P1,P2,P3的值均為0.95.自由空間存在噪聲等多種影響因素,會使傳輸時延不同程度的減慢,仍以噪聲平均功率譜密度σ2分別為1,2 和3 dB/m 情況下討論,設σ2分別為1 dB/m 情況下的傳輸時延為1 μs,2 dB/m 下的時延為1.5 μs,3 dB/m 下的時延為2 μs.

如圖9 所示,吞吐率隨著噪聲功率譜密度的增大而減小,當單側子節點數目為3 時,在噪聲功率譜密度為σ21 dB/m 的自由空間,單頭節點SWGGΛ-TQAN 的吞吐率為245 kb/s,在噪聲功率譜密度為σ23 dB/m 的自由空間,單頭節點SWGGΛ-TQAN 的吞吐率為122.5 kb/s.在噪聲功率譜密度一定的情況下,隨著單側子節點數目的增多,單頭節點SWGGΛ-TQAN 的吞吐率降低.在σ22 dB/m 的自由空間中,當單側子節點數由2增加到7 時,吞吐率由110.6 kb/s 下降到46.45 kb/s.

圖9 單頭節點SWGGΛ-TQAN 中吞吐率與單側子節點數目的關系Fig.9.Relationship between throughput and the number of single side child nodes in single-head node SWGGΛ-TQAN.

根據上述分析,發現單頭節點SWGGΛ-TQAN的單側子節點數目為10,即整體組網數量為21 時,構成如圖3 所示的結構,在σ22 dB/m 的自由空間中,組網的吞吐率只有23.9 kb/s,但若構成圖5 所示的多頭節點SWGGΛ-TQAN,總節點數目仍為21,此時3 個單頭節點SWGGΛ-TQAN 的吞吐率分別為79.83,163.4 和601.7 kb/s.

考慮到組網中節點數量大多情況下不會太少,故多頭節點SWGGΛ-TQAN 更加適用,保證每個單頭節點SWGGΛ-TQAN 的吞吐率不會太低.綜上所述,應根據組網需求的總節點數目,選擇構建單頭節點SWGGΛ-TQAN 或多頭節點SWGGΛTQAN,保證量子組網的吞吐率盡可能大.

5 結論

本文基于雁群空中飛行陣列的特點,提出了基于雁群陣列的量子空中組網構建策略,對該組網構建的可行性進行了理論研究,提出了組網與衛星、網間的兩種通信系統,并對其性能進行了分析.仿真結果表明,SWGGΛ-TQAN 的構建在理論上是可行的,且總節點數目過多時,多頭節點SWGGΛTQAN 具備更好的性能.針對不同總節點數,SWG GΛ-TQAN 可以構建不同的拓撲結構,具有較強的適應性.仿雁群陣列量子空中組網的構建策略為量子通信及空中組網領域的研究提供了新的方向,同時也為后續對該組網的其他研究奠定了理基礎.