稠密流體氮高溫高壓相變及物態方程*

田春玲 劉海燕 王彪 劉福生 甘云丹

1) (西南大學物理科學與技術學院,重慶 400715)

2) (西南交通大學,高溫高壓物理研究所,成都 610031)

3) (西安近代化學研究所,西安 710065)

氮的高溫高壓物態方程以及相圖對于研究和制備高能量密度含能材料至關重要.本文采用基于密度泛函理論的分子動力學模擬方法,研究了液氮的高溫高壓行為,給出 900—25000 K,2—200 GPa 區間流體氮的物態方程以及組分、相態變化.在上述相空間,觀察到流體氮分子相-聚合物相以及聚合物-原子相的相變發生.獲得的液氮Hugoniot 理論曲線與實驗結果吻合較好,發現30—60 GPa 區間Hugoniot 曲線的軟化與分子-聚合物流體相的相變有關;在60 GPa 后Hugoniot 曲線變陡峭與流體氮進入聚合物相區有關.

1 引言

氮的高溫高壓行為一直受到人們的關注,不僅因為全氮化合物有望成為下一代的綠色高能量密度材料,也由于氮氣是炸藥主要反應和爆轟產物,人們在評估含能材料的能量特性和作功能力時需要了解氮的高溫高壓物態方程和相圖[1,2].氮的最外層電子分布為2s22p3,在常溫常壓下氮原子與另外一個原子鍵合,形成配位數為1 的雙原子分子化合物.氮分子中的氮三鍵(N≡N)是自然界最穩定的化學鍵之一,完全打破一個氣相氮分子的N≡N 需要9.74 eV 能量[3].但在高壓條件下,隨著氮分子間距變短,分子間排斥力增大,分子內電子不再局域于分子內部,N≡N 變得不穩定[4];并隨著溫度的升高,N≡N 將斷裂并形成單(N—N)、雙鍵(N=N)鏈接的多原子分子化合物,即聚合氮[2,5?11].2004 年德國Max Plack 研究所Eremets 等[12]首先在2000 K 以及110 GPa 條件下觀察到固氮從雙原子分子晶體轉變為單鍵原子構成的立方偏轉氮(又稱cg-N)結構,即1 個氮原子可與另外3 個氮原子相連形成3 配位的共價鍵化合物.最近,在靜高壓實驗[13?16]中又相繼在150 GPa,2000 K 下發現了一種層狀聚合氮,該層狀聚合氮與黑磷的晶體結構類似,具有褶皺蜂窩層狀結構.此外,通過第一性原理計算人們預言了以單、雙鍵鏈接的N8[10],N10[17,18]等分子形式存在的低壓聚合氮晶體.在固態氮的高溫高壓相變研究如火如荼進行時,流體氮的高溫高壓行為也受到密切關注.

流體氮最早的研究工作可追溯到20 世紀70—90 年代,美國洛斯阿拉莫斯實驗室Dick[19]首先通過炸藥爆炸加載沖擊波測量了液氮在2—43 GPa區間的沖擊壓縮Hugoniot 線;隨后利弗莫爾實驗室[20,21]利用氣炮加載沖擊波技術將液氮沖擊壓縮到20—80 GPa,并測量其沖擊溫度,處于5000—15000 K 間.研究發現液氮的沖擊Hugoniot 曲線在30—60 GPa 區間,相應沖擊溫度為 7000—12000 K時出現軟化現象.最近,國內西南交通大學動高壓實驗研究小組報道了類似的沖擊波壓縮實驗測量結果[22].文獻[23,24]利用了流體變分理論分析認為,流體氮沖擊Hugoniot 曲線軟化現象與液氮在30 GPa 和6000 K 時發生分子相到原子相的轉變有關.近年來隨計算機性能逐步提高,開始采用從頭算模擬方法來研究液氮在高溫高壓極端條件下的行為,包括密度泛函分子動力學模擬(density-functional theory based molecular dynamics,DFTMD)以及路徑積分蒙特卡羅模擬(path integral Monte Carlo,PIMC).普遍認為在中、低溫區間,無需考慮電子的激發效應,DFT 理論比較可靠[25?28].2016 年Driver 等[27]利用PIMC 和DFT-MD 兩種方法對高溫流體氮的性質進行了研究;他們認為密度泛函理論以及交換關聯泛函在T<105K 對于氮的描述是合理的,但在更高溫度下PIMC 方法更可靠.2000 年Kress 等[29]利用DFT-MD 較好地描述了液氮的沖擊Hugoniot 曲線,認為Hugoniot曲線軟化與液氮分子相到原子相的相變有關.Boates 研究小組[30,31]采用DFT-MD 計算液氮的部分溫壓相區的物態方程,提出6000 K 以下分子流體分子氮的離解產物是聚合氮流體,在更高溫度則是原子氮流體.最近,研究發現氫的高溫高壓離解產物是壽命較短的氫原子團簇,并與原子氫(等離子體氫)有明顯區別[32].本文在氮的模擬中同樣發現了大量壽命較短氮團簇聚合物,與原子氮相比它們的分子構型以及電荷密度分布完全不同.在對模擬數據進一步分析后,發現流體聚合氮可能比人們認為的更加穩定,存在溫壓范圍更廣.而液氮沖擊Hugoniot 曲線在30 GPa 和6000 K軟化現象更有可能是發生了分子相到聚合相的相變,而不是氮分子完全離解進入了原子或等離子體相區.

2 研究方法

本文基于密度泛函理論框架下的分子動力學模擬方法,研究了氮在高溫高壓下的物態方程以及相態變化,包括氮的壓強、內能、組分等隨溫度、密度的變化規律.模擬工作采用VASP (Viennaab initiosimulation package)程序[33]完成.模擬超胞含有64 個氮原子(Nt=64),選用的電子交換關聯函數為廣義梯度近似(general gradient approximate,GGA)下的PBE (Perdew-Burke-Ernzerhof)泛函[34,35].為了保證計算的效率和精確度,電子波函數采用截斷能Ecut為1200 eV 的平面波基組,總能量收斂精度達到 10?5eV,受力的精度為 10?4eV .布里淵區的能量積分采用 1×1×1 的網格點設置.分子動力學模擬采用正則NVT 系綜,選用Nosé-Hoover 算法[36]控制離子溫度,離子運動方程的積分以0.5—1.5 fs 時間步長進行計算,模擬時長至少為3 ps.

本文每個數據點的熱力學量采集都在體系到達熱力學平衡后才進行.考慮到氮原子間最大成鍵距離為單鍵鍵長(1.46 ?,1 ?=0.1 nm)[2,37],本工作與前人研究一致,選擇氮原子間的有效成鍵半徑為1.5 ?[30],即在該距離內的原子將與參考原子成鍵.根據成鍵情況對流體氮的組分中不成鍵的孤立氮原子(n=1,配位數為0)、氮原子對(n=2,即配位數為1 的氮分子)以及配位數大于1 的團簇聚合物(n≥ 3)進行統計,并用(Nn) 記錄各組分布居數,組分比Rn定義為體系中各組分的原子數量相對于原子總數的百分比(RnnNn/Nt).而氮分子的離解度(β)指的是構成離解了的分子流體占超胞中原子總數的比例,即β1?2N2/Nt.各組分數Nn、原子的配位數是對達到平衡態的數千步分子動力學模擬軌跡進行統計分析得到的平均值.

3 結果與討論

3.1 流體氮的等容物態方程與分子-聚合物-原子的相變

圖1 和圖2 所示為流體氮在25000 K 范圍內流體氮的兩條等容線.圖1 給出了1.75 g/cm3下流體氮的壓強(圖1(a))、內能(圖1(b))、原子配位數(圖1(c))、組分(圖1(d))隨溫度的變化關系,以及在不同溫度下原子徑向分布函數(圖1(e))以及分子動力學模擬中超胞原子位置分布的隨機抽樣(圖1(f)—(h)).從圖1(a)可見壓強P隨溫度T變化可以明顯分為3 段;在2000—7000 K 范圍,壓強隨溫度單調增大;在7000—10000 K 時,壓強隨溫度升高而下降;此后壓強再次隨溫度升高而增大.

圖11.75 g/cm3 時流體氮的等容線 (a)壓強-溫度關系;(b) 內能-溫度關系;(c)原子平均配位數隨溫度的變化;(d) 化學組分占比(Rn)與離解度(β)隨溫度的變化;(e) 徑向分布函數圖像;(f)—(h)不同溫度下的原子分布抽樣,綠色原子代表氮分子組分,玫色表示聚合物組分,藍色小球表示氮原子組分,紅色三角形代表液氮的Hugoniot 狀態點Fig.1.Fluid nitrogen at 1.75 g/cm3:(a) Temperature-dependence for pressure ;(b) temperature-dependence for internal energy;(c) temperature-dependence for coordination number of atoms;(d) temperature-dependence of chemical component ratio (Rn) and molecular dissociation degree (β) ;(e) pair correlation functions at temperatures of 7000,10000 and 20000 K;(f)–(h) snapshots from MD simulations.Green atoms represent molecules,the red spheres show polymers and the blue indicate isolated atoms.The red triangle represent the Hugoniot point.

在T<7000 K 相應P<24 GPa 時,氮原子的平均配位數(圖1(c))保持在1,從圖1(d)組分分析可見氮分子離解度為0,說明此時體系處于分子流體相.在7000 K≤T<10000 K 時,氮分子離解度快速增大,原子的平均配位數變得大于1,表明體系發生分子-聚合物相變,而非分子-原子相變.氮分子的垮塌造成等容線上壓強負斜率變化((?P/?T)ρ <0),而內能則隨溫度的升高快速增大,斜率變大.組分分析也表明此區間氮分子快速變少,而聚合物較原子組分大幅增大,這揭示出氮分子解離后產生的原子更傾向與剩余分子結合,形成枝鏈狀團簇(原子數目n≥ 3),如圖1(g)所示,而形成孤立原子組分(n=1)的較少;體系是分子、大分子團簇為主的混合物.在T>10000 K 溫度區間氮分子離解速率變緩,以至于分子離解對壓強的負貢獻可以被熱效應的正貢獻相抵消,故壓強再次隨溫度的升高而增大.組分分析可見,聚合物產物在12000 K時占比最大,隨后逐步減少,而原子組分則隨溫度的升高而穩步增加.在溫度到達15000 K 的后,巨大的熱運動動能使得原子間化學鍵極易短裂,組分中聚合物和剩余分子都將進一步分解,孤立原子逐步變成體系主要成分,原子的平均配位數小于1.如20000 K 下流體氮中原子組分占比超過40%,原子的平均配位數也只有0.7 左右,分子動力學模擬中超胞原子分布的隨機抽樣見圖1(h),此時體系逐步過渡到原子為主的流體相.在流體氮從分子-聚合物的轉變中,徑向分布函數(圖1(d))的第一峰的位置從7000 K 情形下的1.10 ?(對應雙原子氮分子的N≡N 鍵長[30])移動到10000 K 下的1.15 ?,表明氮原子間鍵長變長,有N=N(鍵長1.25 ?[38])、N—N(鍵長1.46 ?)生成;在20000 K,34 GPa 的時,徑向分布函數的峰值幾乎完全消失,說明隨溫度升高體系逐步由聚合物向原子相轉變.在聚合物-原子轉變中,壓強連續地隨溫度增大.

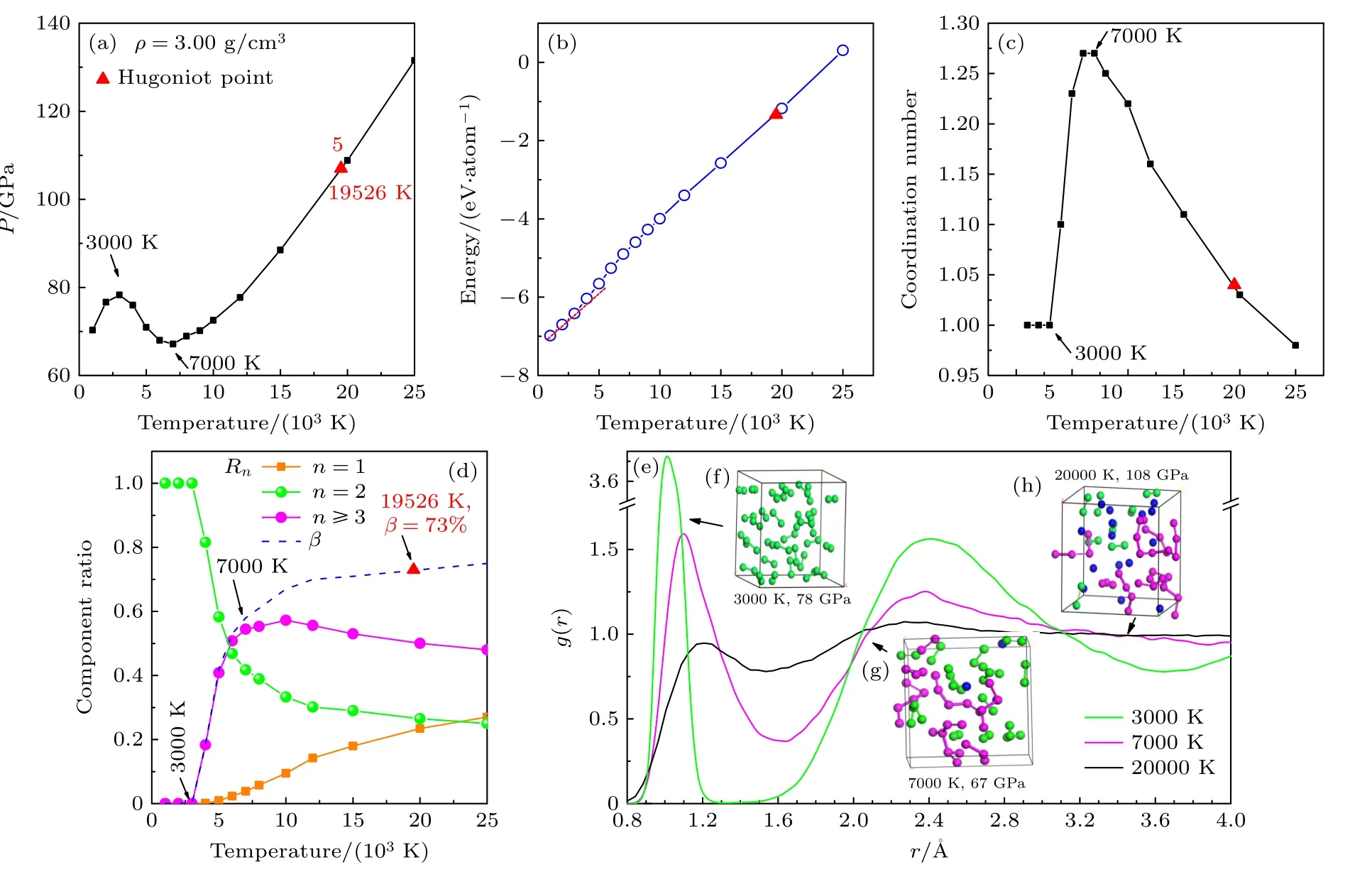
圖23.00 g/cm3 時流體氮的等容線 (a)壓強-溫度關系;(b) 內能-溫度關系;(c)原子平均配位數隨溫度的變化;(d) 化學組分占比Rn 與離解度β 隨溫度的變化;(e) 徑向分布函數;(f)—(h) 不同溫度下的模擬原胞原子的瞬態抽樣Fig.2.Nitrogen isochore at 3.00 g/cm3:(a) Temperature-dependence for pressure ;(b) temperature-dependence for internal energy;(c) temperature-dependence for coordination number of atoms;(d) temperature-dependence of chemical component ratio (Rn) and molecular dissociation degree (β) ;(e) pair correlation functions at temperatures of 3000,70000 and 20000 K;(f)–(h) snapshots from MD simulations at different temperatures.

類似的流體氮從分子-聚合物的轉化造成等容線上壓強負斜率變化現象在3.00 g/cm3時也觀察到,如圖2(a)所示.隨著密度變大,流體氮分子-聚合物相變發生在較低的3000—7000 K 溫度區間,相變前后超胞原子瞬態分布如圖2(f)和圖2(g)所示;此區間壓強隨溫度增大而降低,內能隨溫度的升高而增大且斜率變陡(圖2(b)),體系原子的平均配位數從1 快速上升到1.28 左右(圖2(c)),分子離解度從0 增大到60%,聚合物成分從0 上升到58%,而原子組分不超過2%(圖2(d)).在10000 K左右聚合物組分含量達到峰值,隨后逐步減少,而原子組分一直隨溫度的升高而增大.隨溫度的升高,徑向分布函數的第一峰值逐步降低,位置從1.1 ?向1.3 ?移動(圖2(e)).與1.75 g/cm3情形相比,3.00 g/cm3流體氮中孤立原子組分隨溫度增加極為緩慢;即便在20000 K 的高溫下,熱效應仍不足以使大部分原子克服化學鍵的束縛,變為自由原子為主的流體相;體系組分還是以聚合物居多(52%),原子組分雖然上升到22%,但仍不占優,如圖2(h)所示;即體系仍處于聚合物為主相區,仍未進入原子流體相區.可見,密度(壓強)越大,聚合物-原子流體的相變的溫度越高.

當密度為1.75,3.00 g/cm3時,對流體氮在溫度分別為2000 K,7000 K,20000 K 下的分子動力學模擬中超胞(即圖1(f),(h)和圖2(g),(h))的電荷密度進行計算,結果見圖3.從圖3 可以看出體系中原子的成鍵情況.圖3(a)顯示2000 K 以及1.75 g/cm3下流體氮中雙原子成鍵,表明體系處于分子相;而圖3(b)則顯示20000 K 以及1.75 g/cm3下大多數原子的價電子局域在原子核周圍,成球形,原子間無化學鍵,體系處于以原子為主流體相;圖3(c)和圖3(d)顯示3.00 g/cm3時在7000 K 和20000 K時,體系除了原子、分子外,還有多原子成鍵的N3,N4,N5等大分子團簇存在,并在數量上占優,體系處于以聚合物為主流體相.可見,體系的電荷分布信息也支持流體氮處于分子相、原子相或聚合物相態的判斷結論.

圖3 在不同的溫度和密度下流體氮結構的價電荷密度(a) 1.75 g/cm3,2000 K;(b) 1.75 g/cm3,20000 K;(c) 3.00 g/cm3,7000 K;(d) 3.00 g/cm3,20000 KFig.3.Valance charge densities of fluid nitrogen at different temperatures and densities:(a) 1.75 g/cm3,2000 K;(b) 1.75 g/cm3,20000 K;(c) 3.00 g/cm3,7000 K;(d) 3.00 g/cm3,20000 K.

3.2 Hugoniot 物態方程

在沖擊波壓縮下,波后液氮的內能、壓強、密度滿足Hugoniot 關系式:

其中,E0,P0,ρ0分別是液氮初始狀態的內能、壓強和密度.本文依照液氮Hugoniot 實驗[19?22]對初始條件為T0=77 K,ρ0=0.808 g/cm3,P0=1 atm(1 atm=101.325 kPa)液氮的沖擊壓縮狀態進行了計算,結果見表1,并把理論計算結果與測量結果進行比較,見圖4(a)和圖4(b).

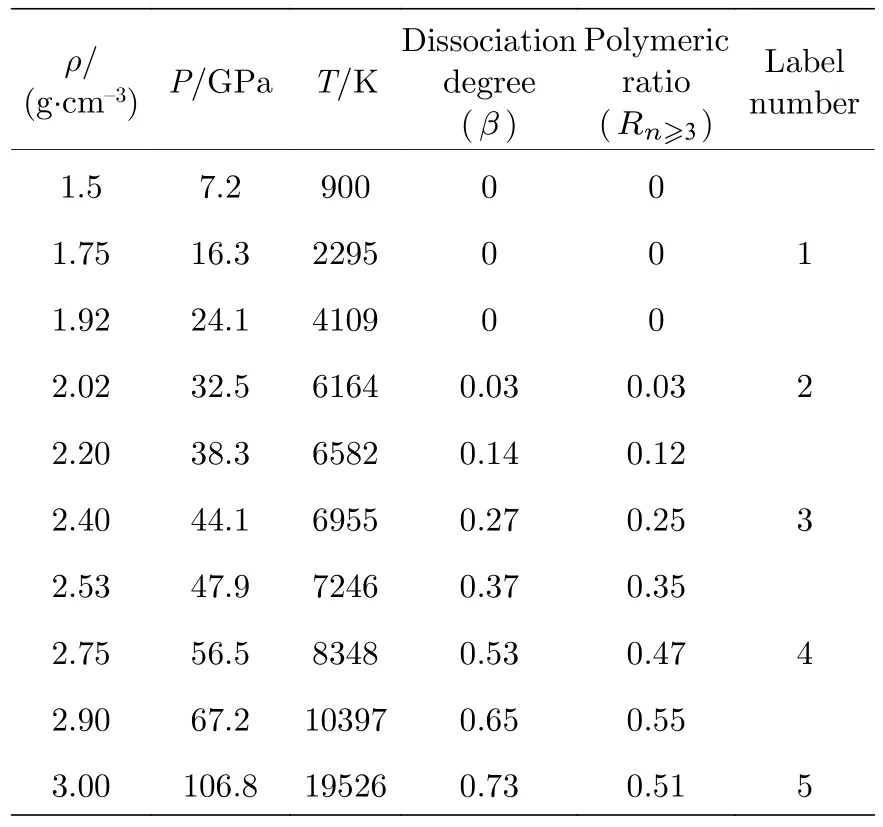
表1 DFT-MD 模擬得到的液氮沖擊狀態數據以及流體組分(初態ρ0=0.808 g/cm3,T0=77.6 K,E0=–8.319 eV/atom)Table 1.Calculated results for pressure and temperature and the chemical components along the Hugoniot curve from our DFT-MD simulations.The initial conditions are ρ0=0.808 g/cm3,T0=77.6 K,E0=–8.319 eV/atom.

圖4 液氮的Hugoniot 物態方程的實驗和理論結果比較 (a)壓強-密度關系;(b)溫度-壓強關系Fig.4.Comparison between the experiments and calculations of Hugoniot equation of state for liquid nitrogen:(a) Pressure as a function of the final shock density;(b) shock temperature as a function of the pressure.

本文計算得到的液氮Hugoniot 沖擊壓縮線與實驗測量結果[19?22]符合得較好(圖4(a)),在30—60 GPa 區間Hugoniot 線出現軟化現象,在高于60 GPa 壓力區間Hugoniot 線再次變陡峭.在Hugoniot 線出現軟化時,沖擊溫度隨壓強上升趨勢也變緩(圖4(b)).圖4(b)給出此區間的溫度理論估值在6000—10000 K,略低于實驗值7000—12000 K,同時給出了Kress 等[29]的從頭算結果以及Ross 的經驗模型計算結果進行比較.對于沖擊溫度,本文計算結果與Kress 等[29]的從頭算結果均略低于實驗值,但整體趨勢與實驗是一致的.Ross[23]的經驗模型對沖擊溫度描述和實驗結果較吻合,但Ross[23]的經驗模型對Hugoniot 線在壓強超過60 GPa 變硬的趨勢很難描述.

為了對液氮Hugoniot 物態方程的變化特征做出解釋,對Hugoniot 線上的5 個狀態(在表1 和圖4 標號為1,2,3,4,5)點進行分析,它們的密度分別為1.75,2.02,2.40,2.75 和3.00 g/cm3.這些沖擊壓縮狀態分別處于相應等容線斜率為正的分子相區,斜率為負的分子-聚合物相變區以及斜率為正的聚合物相區.其中,沖擊壓縮密度為1.75 g/cm3狀態1 的壓強為16.3 GPa,沖擊溫度為2295 K(見圖1 紅色),它位于等容線的分子相區,體系離解度為0.沖擊壓縮密度為2.02 g/cm3的末態2,對應沖擊狀態(33 GPa,6164 K)剛好進入等容線的負斜率區間(如圖5(a)所示),體系原子分布抽樣如圖5(b)所示;此時體系離解度為3%,表明分子-聚合物相變剛開始.沖擊壓縮密度為2.40 g/cm3的末態3 正處于等容線的負斜率區(如圖5(c)所示),即體系處于分子-聚合物相變區,對應沖擊壓強約為44 GPa,沖擊溫度理論值為6955 K;此時約有27%的分子離解,并且產物絕大多數為聚合物(25%),體系原子分布抽樣如圖5(d).當沖擊壓縮密度到達2.75 g/cm3時,對應狀態4 (如圖5(e)所示),相應的沖擊壓強約為57 GPa,沖擊溫度計算值為8348 K,該狀態處于等容線負斜率區的終點附近;此時過半的分子(53%)已離解,絕大多數產物是聚合物(47%),見圖5(f)和圖5(g);意味體系跨過分子-聚合物相變區間,剛進入聚合物相區.在3.00 g/cm3的沖擊狀態5 (107 GPa,19526 K)處于等容線的正斜率相區((?P/?T)ρ >0,如圖2紅色所示),其中聚合物占51%,原子只占22%,剩余是分子,體系組分構型抽樣如圖2(h),意味體系處于聚合物為主的流體相.

圖5 液氮的Hugoniot 沖擊 壓縮點在不 同等 容線上的壓 強-溫度相空 間分布 (a) 2.02 g/cm3;(c) 2.40 g/cm3;(e) 2.75 g/cm3;圖(b),(d),(f)是與圖(a),(c),(e)相對應的分子動力學模擬中原胞原子位置分布的的瞬態抽樣.(g) 2.75 g/cm3 下流體氮的組分Fig.5.Hugoniot points in P/T space at constant densities:(a) 2.02 g/cm3;(c) 2.40 g/cm3;(e) 2.75 g/cm3;(b),(d),(f) corresponding snapshots from MD simulations of panels (a),(c),(e).(g) Chemical components at 2.75 g/cm3.

理論計算結果表明,在狀態2 和4 之間的30—60 GPa 沖擊壓強區域,體系處于分子-聚合物的相變區,由于分子的垮塌導致壓強減小,因此實驗上會觀測到Hugoniot 線軟化現象,并且得到的格林乃森參量為負().在該區域由于體系吸收的沖擊波能量相當部分將用于打破分子鍵能的束縛,導致沖擊溫度(熱效應)升高緩慢.在沖擊狀態4 (P≈60 GPa)時,體系完成分子-聚合物相變.此后,流體氮進入聚合物相區,體系沖擊壓強和沖擊溫度快速上升,Hugoniot 線變陡峭.本文理論模擬完美地解釋了Hugoniot 線30—60 GPa 區間軟化現象以及P>60 GPa 后變陡峭的測量結果.研究表明實驗觀察到液氮Hugoniot線的軟化與流體氮的分子-聚合物相變有關,而非分子-原子流體相變導致,而聚合氮存在溫壓相區遠高于目前認為的6000 K 的溫度下.對于沖擊溫度,本文理論結果略低于實驗值,可能原因是選用的交換相關泛函沒有考慮色散相互作用而導致較多的分子離解,因為最近有研究[28]表明范德瓦耳斯相互作用將增加氮分子的穩定性.

4 結論

本文采用DFT-MD 方法研究了高溫高壓條件下氮的鍵合方式、組分演化與相態變化及其對熱力學性質的影響.結果表明液氮分子相-聚合相的相變將導致等容線上壓強隨溫度負增長變化.研究發現在30—60 GPa 區間Hugoniot 線的軟化由液氮分子相-聚合相相變所致;在沖擊壓強高于60 GPa時,流體氮進入聚合氮為主相區,Hugoniot 線變硬.在目前實驗所能達到20000 K 以及100 GPa沖擊壓縮狀態下,原子氮流體組分只占20%,聚合物占51%,體系仍處于聚合物為主流體相,而非原子流體相.本文計算結果較好地解釋了Hugoniot物態方程測量結果,表明聚合物流體相可能存在溫壓相區更廣,遠超過目前認為6000 K 溫度范圍.