Meteodyn WT軟件的大氣熱穩定度影響研究

袁紅亮，王 炎，陳 彬，宋俊博

(中國電建集團西北勘測設計研究院有限公司,西安 710065)

0 前 言

在碳達峰碳中和的背景下，風電作為新能源產業中的重要一環，對實現“30·60”戰略目標將發揮重要的作用。風能資源評估在風電開發過程中起著關鍵的作用，隨著風電開發建設的進度逐漸加快，各種風能資源評估軟件應運而生，軟件根據用戶輸入的地形、大氣熱穩定度、粗糙度等參數進行邊界條件的生成，繼而進行風電場流場模擬[1]。其中，大氣熱穩定度在風能資源評估中是非常重要的參數，不同的大氣熱穩定度代表不同的大氣層結特性，其取值不同會導致不同的流場模擬結果，繼而影響風能資源評估的準確性。為了研究大氣熱穩定度對風能資源評估的影響，多位學者對其進行了相關研究。Gualtieri詳細分析了荷蘭Cabauw地區10、20、40、80 m測風塔的大氣熱穩定性與風切變指數的時間變化關系[2]。研究發現，相對于對數定律，冪定在不穩定和中性層結條件下給出更接近實際的風廓線[3-5]。然而，目前基于Meteodyn WT軟件進行大氣熱穩定度的設置及其影響研究較少。在實際工程計算中，風電場大氣熱穩定度應根據工程實際情況進行取值。一般情況下，工程師都采用軟件默認的值，這種大氣熱穩定度取值方法雖然簡便，但無法反映場風電工程的真實情況，也無法保證計算的精確性。

本文以某風電場工程為例，研究Meteodyn WT軟件中不同大氣熱穩定度取值對風速、風切變指數及風廓線的影響，提出大氣熱穩定度取值的相關方法及建議，為風電工程中合理地對大氣熱穩定度進行取值提供參考。

1 Meteodyn WT軟件和大氣熱穩定度簡介

Meteodyn WT軟件是法國美迪公司專門為解決大氣邊界層問題而設計的軟件，采用計算流體力學的方法(CFD)進行空間風流模擬，在限定邊界條件下，數值求解三維雷諾平均納維—斯托克斯(RANS)方程，并應用適合的湍流模型對目標區域的風流特性參數進行求解計算[6-7]，得到整個場區的風流情況，可用于風能資源評估與發電量計算。該軟件減少了復雜地形條件下計算的不確定性，因此對于復雜地形風電場的風能資源評估具有較好的適用性[8]，同時也適用于平坦地形風電場。

Meteodyn WT軟件中的大氣熱穩定度通過Obukhov長度來定義，該長度可以反映機械性湍流與熱力效應產生的浮力湍流之間的相對主導性。Meteodyn WT軟件的CFD計算中共有 10 個不同的大氣熱穩定度等級可以選擇。大氣熱穩定度等級從 0(非常不穩定)至 9(強穩定)穩定度逐漸提高。表1列出了不同熱穩定度等級下對應的 Obukhov 長度。

Meteodyn WT軟件中大氣熱穩定度對入口風廓線的影響見圖1 。從圖1中可以看出，大氣越穩定，入口風切變越大；同時場區內的風切變也越大。

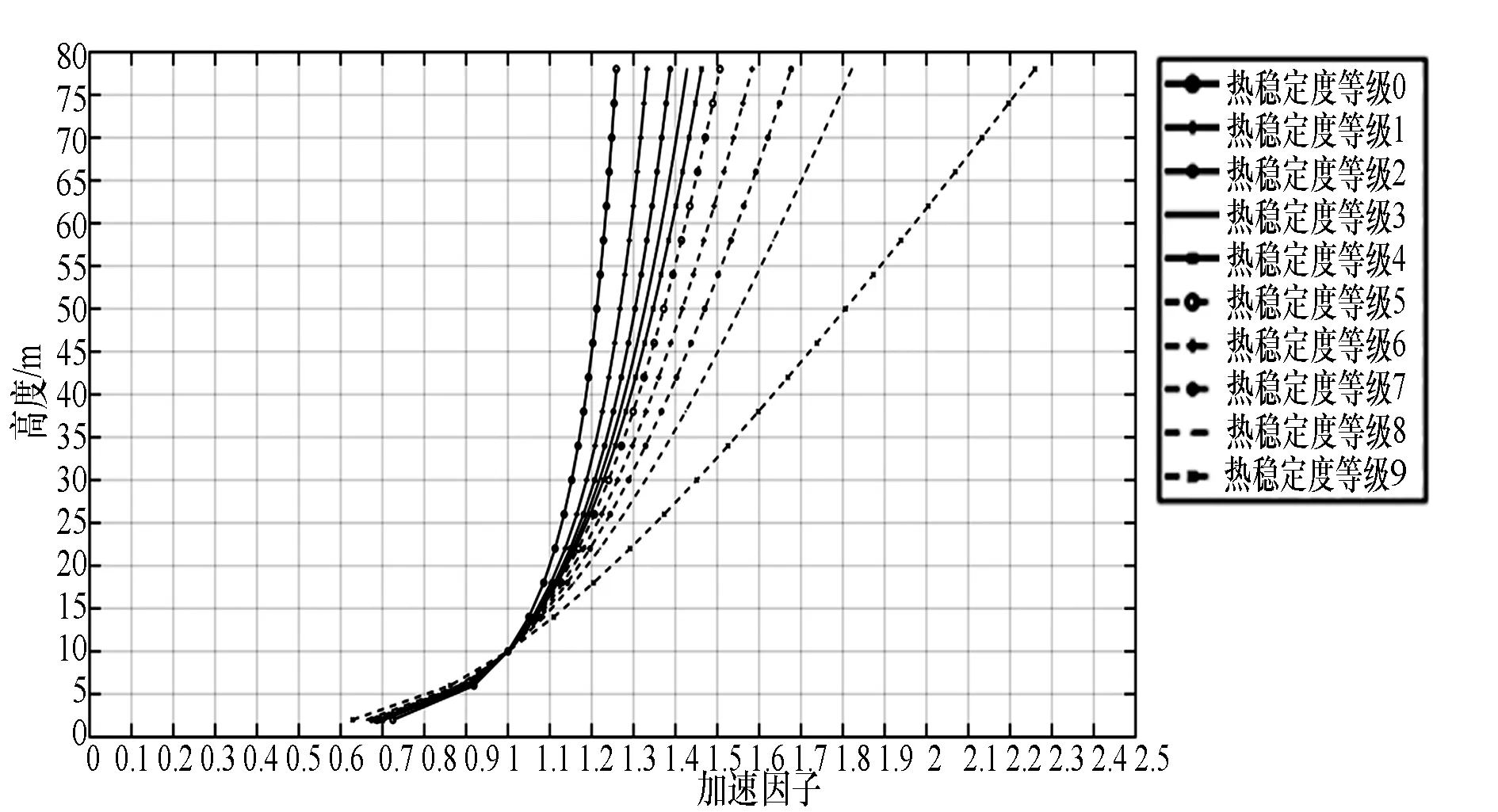
圖1 不同的熱穩定度條件下的入口風廓線

2 算例概況

本文選取的某風電場為我國中原地區平坦風電場，地表主要為農田和村莊。風電場內共有3座測風塔，分別為01、02、03號。3座測風塔高度均為100 m高，風速觀測高度均為100(1)、100(2)、80、60、40、10 m，風向觀測高度均為100、80、10 m。風電場的主風向以北風、南風和南西南風為主。測風塔位置如圖2所示。

圖2 某風電場測風塔位置

為了比較不同大氣熱穩定度取值下測風塔互相推算模擬的準確性，本文選取3座測風塔同期時段為2016年1月1日至2016年12月31日的100 m高度測風數據。

3 計算方案

選用實測1∶2000 數字化地形圖，通過 Meteodyn WT 軟件對真實地形建模。在3座測風塔代表年實測數據、功率曲線、粗糙度等其它輸入參數確定的前提下，大氣熱穩定度是影響風能資源評估的關鍵因素。本文研究方法是在保證其它參數一致的情況下，改變Meteodyn WT軟件中大氣熱穩定度的取值，以此分析大氣熱穩定度對風速、風切變指數及風廓線的影響。具體步奏如下：

第1步,初始建模。根據實測測風數據和場區實測1∶2000地形圖，利用 Meteodyn WT 軟件模擬場區內的風能資源分布情況。初始模型定向計算相關參數設置為：最小水平分辨率為60 m，最小垂直分辨率為5 m，熱穩定度等級初步選擇2(中性)，粗糙度直接引用Meteodyn WT軟件內置的地理信息數據庫，風向扇區間隔為 22.5°。按照上述參數設置進行CFD定向計算直至收斂。

第2步，模型檢驗。采用03號測風塔作為參考塔對初始模型進行檢驗。根據03號測風塔數據進行綜合計算，將Meteodyn WT 綜合計算結果發送至 Windographer FMV，對03號測風塔位置處的模擬風廓線和實測風廓線進行對比分析，以檢驗初始模型對實際風場的擬合是否符合。初始建模得到的參考塔模擬風廓線與實測風廓線的對比見圖3。可以看出，風廓線模擬效果并不好。另外，根據參考塔全風向平均實測風切變指數為0.362，而初始模型模擬的全風向平均風切變指數為0.160，該初始模型經檢驗明顯與實際風場有較大偏差。

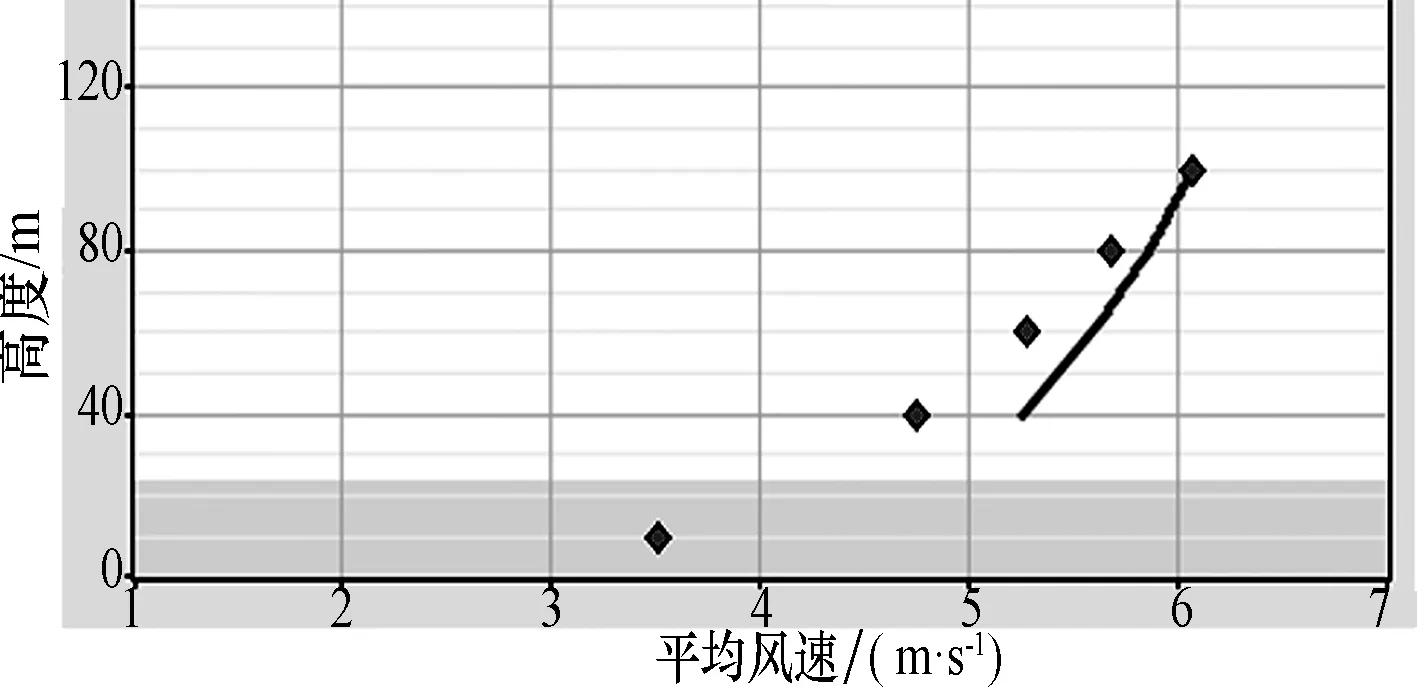
圖3 初始模型中 03號模擬風廓線與實測風廓線對比大氣熱穩定度

第3步，模型校正。針對初始模型與實際風場不符的情況，可以考慮調整的影響風廓線及風切變的參數有：地形精度、地表粗糙度、森林模型、大氣熱穩定度。本文在保證地形精度、地表粗糙度、森林模型等其它參數與風場實際相符的條件下，只調整大氣熱穩定度的取值，以此分析大氣熱穩定度的影響。

在此提出風切變校正法對大氣熱穩定度進行調整，以使校正后的模擬結果更接近風場實際。大氣熱穩定度的風切變校正法參考塔位置處的全風向平均模擬風切變指數、模擬風廓線與實測值不符時，改變大氣熱穩定度的取值重新進行模型綜合計算，直至模擬風切變指數與實測風切變指數接近，誤差較小(根據工程經驗誤差絕對值小于0.04)；且模擬風廓線與實測風廓線較為相符，則認為該取值對應的大氣熱穩定度為最終值，能最大程度反應風場實際。

針對算例，本文初擬8種計算方案，對模型進行校正，采用風切變校正法來確定算例中大氣熱穩定度的取值。具體計算方案見表2。

表2 大氣熱穩定度計算方案

4 計算結果

將算例風場內的其中一座測風塔作為參考塔，利用其100 m高度實測數據對其它2座測風塔位置處100 m高度的風速、風切變指數和風廓線進行模擬，然后與實測風速、實測風切變指數(不考慮10 m高度)、風廓線進行對比，對3座測風塔模擬的風速、風切變指數誤差取絕對值后進行平均，得到8種計算方案的模擬誤差結果見表3、圖4～5。

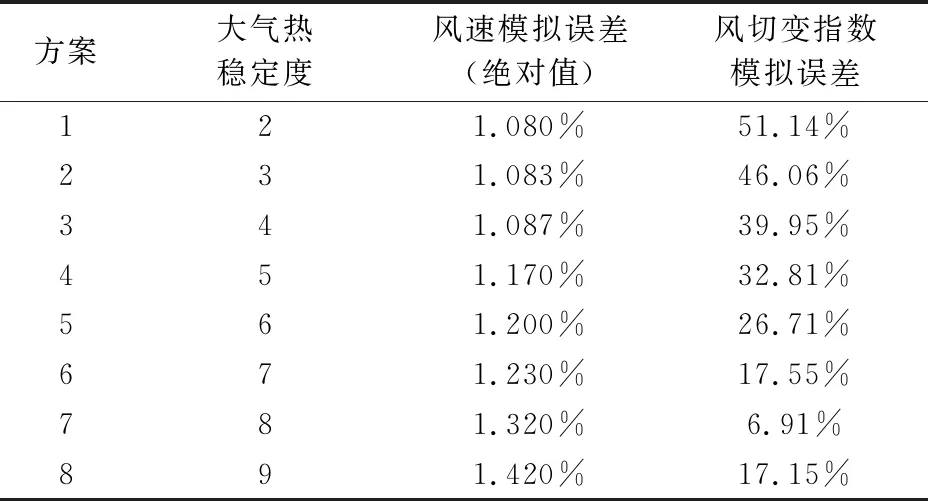
表3 各方案風速、風切變指數模擬誤差表

由上述模擬誤差圖表可以看出：

(1) 隨著大氣熱穩定度的增大，模擬的風速誤差不斷增大，其中最大值為1.420%，最小值為1.080%。

(2) 風切變指數模擬誤差在熱穩定度為8時最小。之后隨著熱穩定度的減小，風切變指數模擬誤差增大。

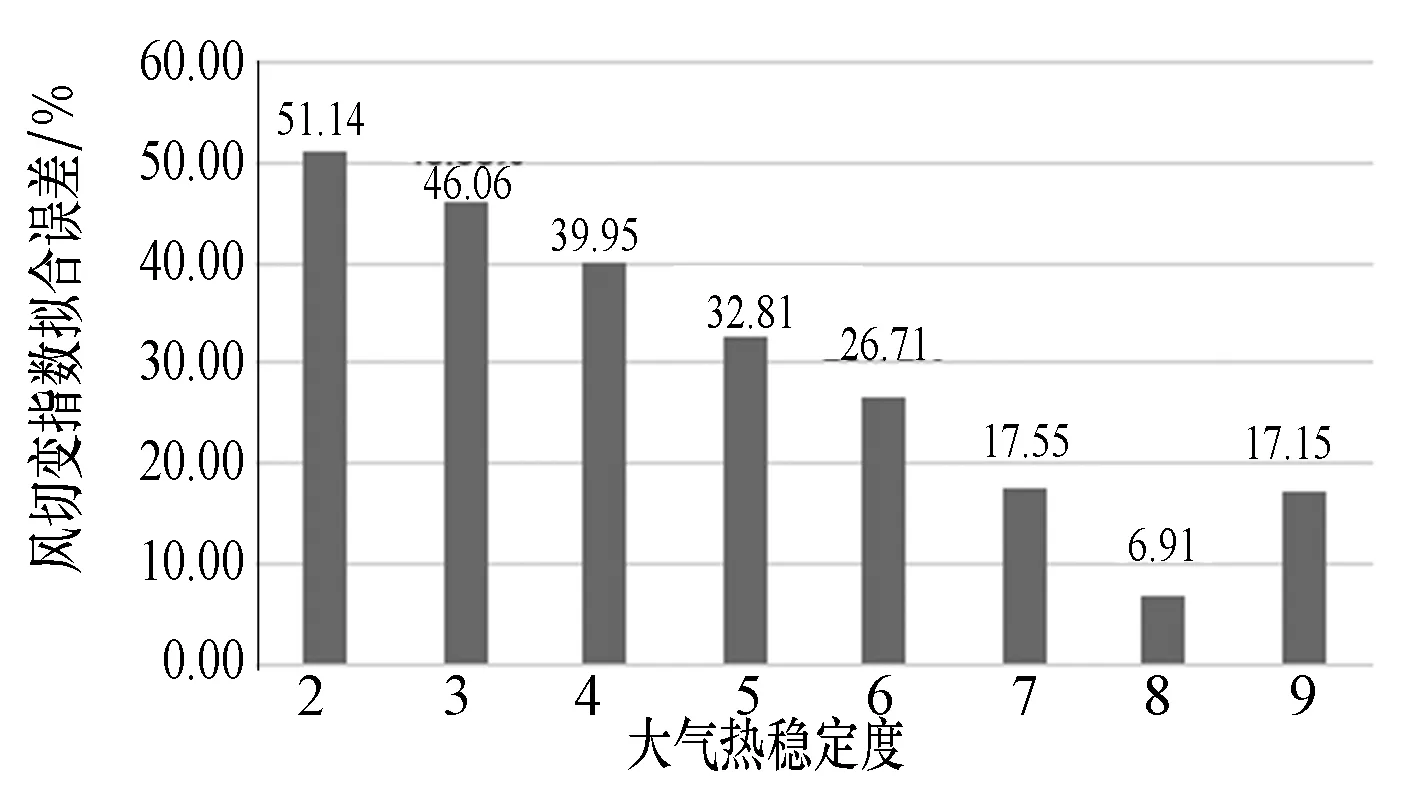
圖5 不同大氣熱穩定度風切變指數模擬誤差

(3) 熱穩定為2時，模擬的100 m高度風速誤差相對最小，但風切變指數模擬誤差較大，風廓線擬合較差，說明此時模型只在100 m高度的平面上具有一定的精度，在垂直方向上與實際風場相差較大，風廓線擬合效果較差。

(4) 綜合上述成果，采用風切變校正法，綜合考慮風速、風切變指數模擬誤差結果，算例中大氣熱穩定度取值應為8。

各測風塔的風速、風切變指數模結果見表4和表5。可以看出，風速模擬的誤差在0.00%～2.23%之間，誤差絕對值平均為1.32%，模擬結果精度較高，誤差較小；風切變指數模擬誤差絕對值在0.001～0.035，風切變誤差最小。

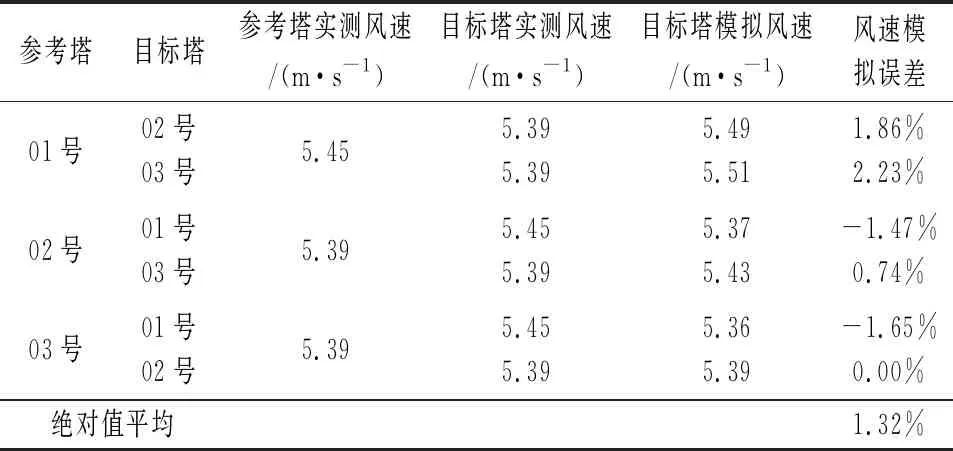
表4 大氣熱穩定度取8時各測風塔風速模擬結果

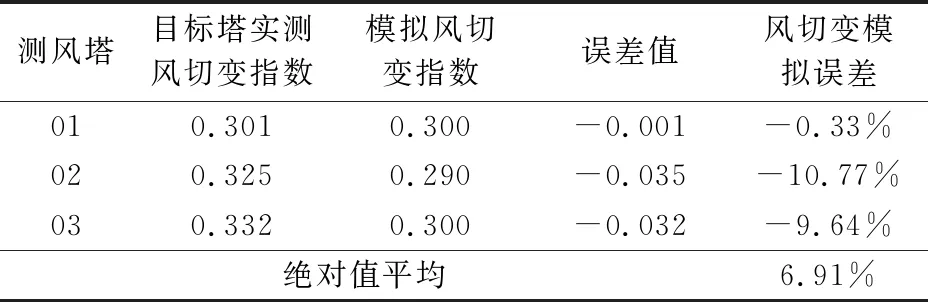
表5 大氣熱穩定度取8時各測風塔風速模擬結果

03號測風塔風廓線模擬結果見圖6。可以看出，風廓線擬合結果較初始模型(圖3)有了很大改善，由此可認為經風切變校正法校正后的模型與實際風場符合。

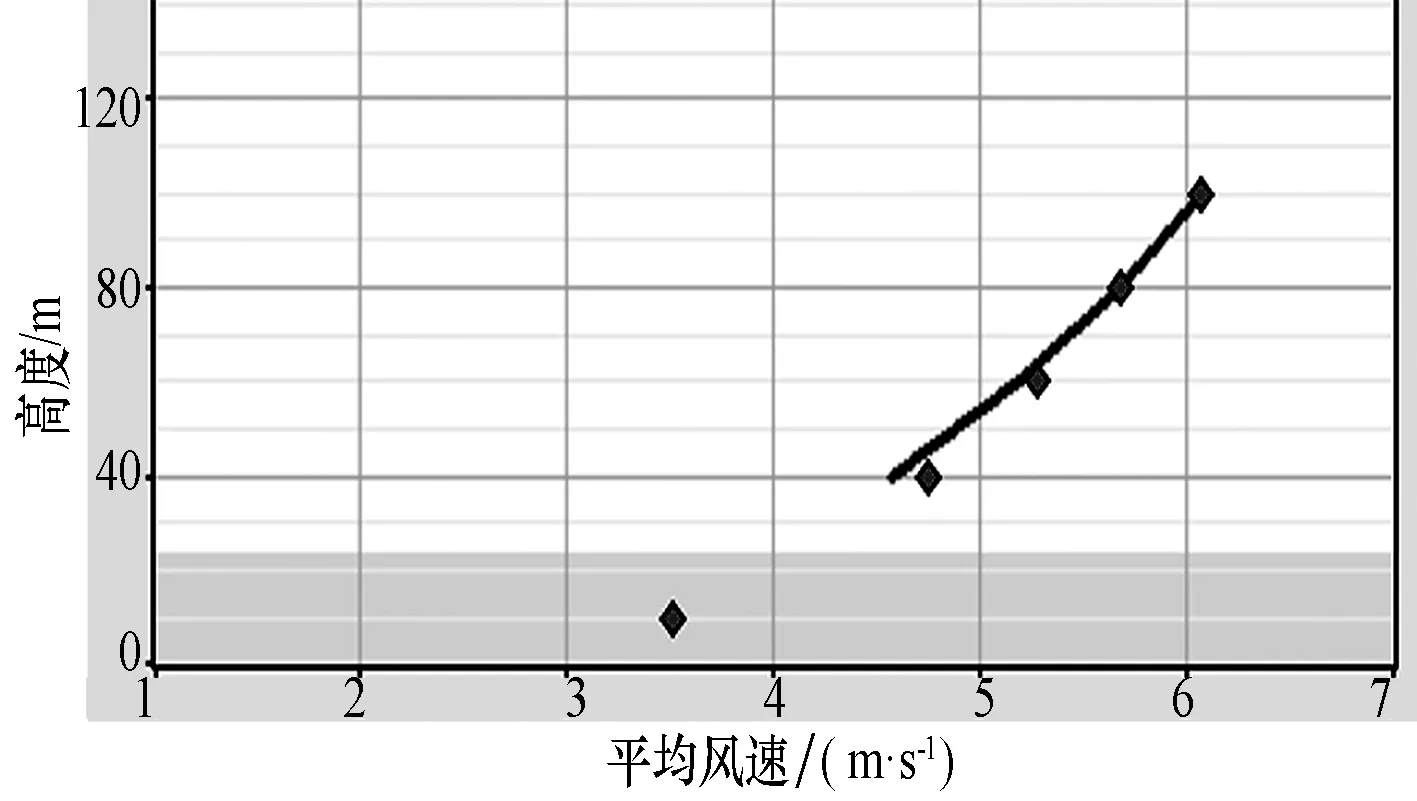
圖6 03號測風塔的模擬風廓線與實測風廓線對比(大氣熱穩定度取8)

5 結 論

通過對Meteodyn WT中大氣熱穩定度取不同值對算例的模擬結果進行分析，評估了大氣熱穩定度對風速、風切變指數、風廓線的影響。并提出了風切變校正法，用來確定大氣熱穩定度的最終取值，形成結論如下：

(1) 算例中，當熱穩定度為8時(非常穩定)，風速模擬的誤差在0.00%～2.23%，誤差絕對值平均為1.32%，模擬結果精度較高；風切變指數模擬誤差絕對值在0.001～0.035，風切變誤差最小。且風廓線擬合較好，模型與實際風場較為符合。

(2) 中原地區的平坦風電場，地表主要為農田和村莊的條件下，隨著大氣熱穩定度的增大，模擬的風速誤差不斷增大，但模擬的風切變指數誤差不斷減小。

(3) 實際工程中，可采用風切變校正法對大氣熱穩定度進行調整，可使校正后的模擬結果誤差更小。

(4) 大氣熱穩定度的最終取值，應結合風切變校正法和風廓線模擬的符合度綜合確定。