管廊燃氣爆炸載荷特征及作用效應研究

鐘冬望 李騰飛 何 理,3 楊志龍 陳江偉

(1.武漢科技大學理學院,湖北 武漢430065;2.湖北省智能爆破工程技術中心,湖北 武漢430065;3.江漢大學爆破工程湖北省重點實驗室,湖北 武漢 430056;4.中國建筑第七工程局有限公司,河南 鄭州 450004)

管廊內部包含燃氣管道、電力管線、自來水管道 等各種能源管線，是城市正常運行的重要保障。燃氣發生泄漏和爆炸的事故時有發生，嚴重威脅著城市安全和居民的生命財產安全。由于燃氣爆炸的破壞效果受到濃度[1]、點火能[2]、點火位置、結構類型[3]等因素的影響，管廊內燃氣爆炸超壓傳播和破壞效應與常見的街道燃氣偶然爆炸相比要更為復雜。因此對管廊燃氣爆炸倉內超壓作用特性和過程進行研究具有十分重要的現實意義。

目前，國內外學者主要通過數值模擬方法對管廊燃氣爆炸效應進行了探索研究[4]。劉希亮等[5-6]基于流固耦合和ALE多物質算法研究了燃氣爆炸沖擊波、不同截面形狀對管廊結構的影響，并認為在爆源附近會形成負壓區;王成等[7]通過小尺度管道試驗研究了不同初始條件下甲烷—氧氣混合氣體爆炸火焰傳播的規律;彭培等[8]對混凝土砌體墻在燃氣爆炸荷載作用下的性能進行了研究，并結合LS-DYNA軟件對砌體結構進行了簡化模擬，并給出了砌體結構加固建議;孫加超等[9]同樣采用LS-DYNA軟件對管廊模型進行了燃氣爆炸數值模擬，得到了倉內的超壓時程曲線和管廊的破壞形式;陳長坤等[10]基于流固耦合算法對管廊在燃氣爆炸荷載作用下的動力響應規律進行了探究。可見，LS-DYNA軟件對于結構在燃氣爆炸荷載作用下的動力響應過程模擬效果較好、應用廣泛。對于燃氣的泄漏過程一般采用Fluent、FLACS等流體力學數值模擬軟件進行分析，例如，韓永華等[11]利用FLACS軟件對燃氣泄漏過程和爆炸效果進行了模擬，提出了提升空間爆炸安全韌性的防護措施，數值模擬軟件的作用越來越顯著，已成為科學研究的重要手段。

由于管廊結構尺寸大，且燃氣爆炸不穩定因素較多，近年來，大型模型試驗開展的較少[12]。BEAK等[13]分別進行了靜力加載試驗和氣體爆炸試驗，對比研究了氣體爆炸荷載與靜態荷載的作用差異。孫松等[14]搭建了2 m×1.2 m×0.6 m(長×寬×高)的爆炸容器，對不同濃度乙烯爆炸超壓場進行了研究;張秀華[15-16]在大型核爆炸模爆器內對乙炔空氣混合氣體開展了結構抗爆的可行性研究，并利用數值模擬方法對TNT和燃氣爆炸產生的沖擊波載荷進行了對比分析。

綜合上述成果分析發現，現有研究傾向于采用數值模擬方法進行燃氣爆炸過程和結果的研究，成果雖然在一定程度上能反映燃氣爆炸的作用效果，但在模型試驗和現場試驗等方面涉及較少。為此，本研究對管廊內燃氣爆炸荷載特性進行理論分析，推導出管廊結構最大位移響應計算公式，通過模型試驗得到管廊燃氣倉爆炸超壓場分布特征，并基于數值模擬結果與試驗結果對推導的公式進行驗證，為管廊燃氣爆炸荷載作用研究提供一定的理論和試驗依據。

1 燃氣爆炸荷載作用下結構位移響應的理論推導

燃氣爆炸荷載作用于管廊燃氣倉壁面屬于非周期激勵的暫態響應，假設燃氣倉壁面所受的爆炸荷載為P(t)，其運動學方程為

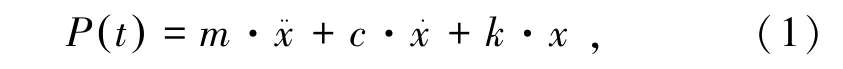
式中，t為時間，s;m為倉壁的質量，kg;為加速度，m/s2;c為粘性阻尼系數;為速度，m/s ;k為系統的剛度，N/m;x為位移，m。

在t=τ至t=τ+dτ的時間微元內，燃氣爆炸荷載產生的沖量為P(τ)dτ，由沖量定理可得，燃氣倉壁在沖量作用下導致的速度增量為

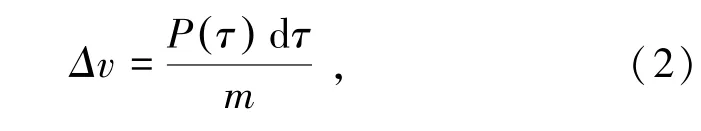
式中，Δv為速度增量，m/s。

因此燃氣倉壁面產生的位移增量為

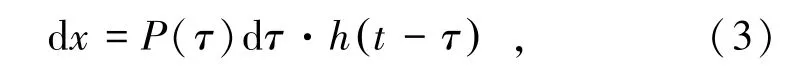
式中，h(t-τ)為用單位脈沖響應函數表示的瞬態響應過程，根據燃氣倉壁面初始條件位移x(0)=0，初始速度(0)=，可以將h(t-τ)簡化為無阻尼的保守系統下的單位脈沖響應函數h(t):

式中，自振周期ω=ωd=ωn，ωd為有阻尼固有頻率，ωn為無阻尼固有頻率;對于無阻尼的保守系統，阻尼比ζ=0。

根據線性系統的疊加原理，在零初始條件下引入Duhamel積分(式(5))，并將式(4)代入式(5)中，得到燃氣倉壁面的位移響應函數x(t)(式(6)):

于是，式(6)可進一步化為:

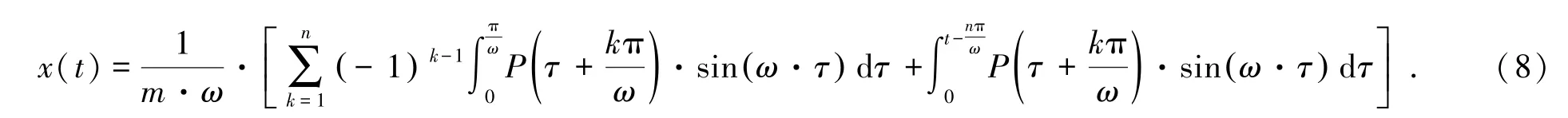
通過將燃氣爆炸荷載作用下燃氣倉壁的響應切分為(n+1)份，可將每一份都看作是一個沖量，則在前n份中每相鄰的兩個沖量之間的作用恰好相反。如圖1中將經典燃氣爆炸荷載切分成多個沖量，對于該種情況下應考慮極限情況，峰值處響應最不利情況為前n個沖量剛好相互抵消，而第(n+1)份恰好位于燃氣爆炸荷載作用的峰值區域;峰值處響應最有利情況則是前n份沖量的作用并不能相互抵消。考慮燃氣爆炸載荷變化較慢，第(n+1)份沖量最多有一半用來抵消前n份沖量的作用，因此管廊結構在燃氣爆炸荷載作用下的最大響應為作用于結構爆炸超壓峰值的0.5～1.0倍，考慮極限情況得到的最大響應峰值計算公式為式中，Pm為燃氣爆炸荷載的壓力峰值，Pa，Xm為管廊燃氣倉壁的位移峰值，m。式(8)使用范圍應滿足爆炸荷載加載時程較長的特點。

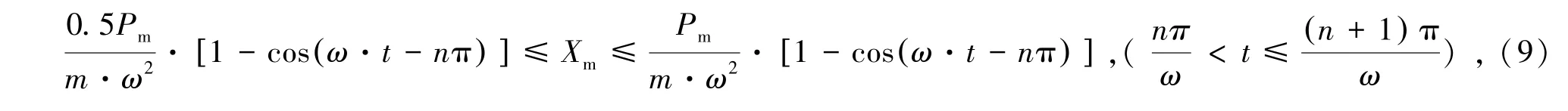
圖1 經典爆炸壓力—時程曲線Fig.1 Classical blasting pressure-time history curve

2 管廊燃氣爆炸相似模型試驗研究

2.1 物理模型制作及傳感器布置

澆筑管廊實體結構的鋼筋混凝土材料模型，模型整體呈長方體，長400 cm，共分3個倉室，上部倉室為通行倉，下部左右倉室分別為電力倉和燃氣倉。其中，燃氣爆炸主要發生在燃氣倉中，試驗布置及實體模型如圖2(a)所示。模型截面尺寸為長170 cm、高210 cm，管廊內部用于隔離各個倉室的隔墻除了燃氣倉與電力倉間隔墻壁厚為15 cm外，其余壁厚均為20 cm，各倉室的具體尺寸如圖2(b)所示。

圖2 綜合管廊試驗模型Fig.2 Experimental model of integrated pipe gallery

模型制作完成后，將開挖的土回填至與管廊頂部平齊，并通過振動搗實機壓實管廊模型兩側回填區域，使周圍土質情況復原，模型燃氣倉軸向方向兩端通過木板進行密封。

根據管廊模型的具體尺寸，在燃氣倉內一共布置了4個壁壓式沖擊波傳感器，傳感器布置方案如圖3所示，從管廊左側倉門50 cm開始以75 cm為間距安裝1#～4#壁壓式沖擊波壓力傳感器。

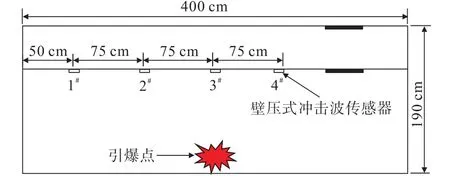
圖3 壓力傳感器布置Fig.3 Layout of the pressure sensors

2.2 燃氣充裝與爆炸激發裝置

通過如圖4所示的天然氣鋼瓶及減壓系統給管廊燃氣倉充氣，并在燃氣倉兩端使用攪拌裝置加速氣體的擴散運動，并將濃度檢測儀置于濃度檢測口中實時監測容器中燃氣濃度，待達到燃氣爆炸極限停止充氣，測定燃氣濃度穩定數值，重復前述步驟直至濃度示數穩定在試驗設計濃度，立即對爆炸容器進行密封。通過無線遙控器遠程控制對燃氣倉內點火頭進行通電，繼而引爆倉內的燃氣。

圖4 物理模型試驗系統Fig.4 Physical model test system

2.3 沖擊波壓力—時程曲線特征

相較于凝聚態炸藥爆炸，可燃氣體爆炸具有爆炸壓力加載速率慢、峰值壓力低的特點[17]，其升壓時長可以達到數百毫秒，爆炸超壓總作用時長可以達到秒級[18]。根據相關學者的研究，燃氣爆炸的超壓過程存在明顯的3個階段，在圖1中OA段為緩慢升壓階段，AB段為快速升壓階段，BC段為壓力下降階段。由于壓力傳感器信號采集設備采用觸發式采集方式，故而對OA段緩慢升壓段未能完整記錄。

在試驗中采用薄木板與結構膠對管廊兩端進行密封，以保證在起爆前氣體不會發生泄漏，其抗壓強度可以忽略不計，管廊內部的超壓作用形式較為簡單，與一般氣體爆炸呈現的多峰值特性[19]不同。試驗中選取的甲烷燃氣濃度為9.5%和10%，濃度接近甲烷反應的最佳理論濃度，不會出現由濃度過低導致二次超壓現象[20]。實測的超壓—時程曲線見圖5。

圖5 典型超壓—時程曲線Fig.5 Typical overpressure-time history curves

由圖5可知:在爆炸超壓作用下3#測點與1#測點的超壓時程曲線反映出，爆炸超壓的升壓時長為500～700 ms，下降時長為900～1 100 ms。不同引爆方式對燃氣爆炸的升壓時長存在顯著影響，根據文獻[21]中的試驗結果，在甲烷濃度為9.5%的情況下采用電火花引爆方式的升壓時長為157.8 ms。本試驗中的甲烷燃氣爆炸升壓時長要明顯大于文獻[12]中的結果，這是由于本試驗模型尺寸大于前者，由于爆轟速度和模型密封性能等因素的影響，導致爆炸超壓升壓時長較大。

在1#測點的超壓—時程曲線的初始階段存在負壓區，并且負壓值在短暫增大以后超壓便由負壓轉為正壓。原因是:1#測點距離引爆點較遠、靠近倉門，甲烷與氧氣發生反應的初始階段會快速消耗甲烷與氧氣生成二氧化碳和水，反應產物在反應區域聚集來不及散開，導致燃氣倉內氣體分布不均，中心反應區壓力升高而倉門等角落區域便形成負壓，但該負壓并不能使得倉門發生破壞，最終在反應生成高溫高壓氣體后使得倉內超壓將倉門推開，壓力得到釋放。

2.4 沖擊波壓力分布規律

管廊模型兩端的木板在升壓過程中在壓力作用下脫落，形成了半自由空間的甲烷燃氣爆炸模型，該模型下管廊燃氣倉內壁的壓力峰值分布特征如圖6所示。根據理論計算及已有試驗結果[22-25]，分析發現甲烷燃氣爆炸破壞最不利結果濃度為9.5%。因此設置了甲烷濃度為9.5%和10%兩種濃度梯度試驗，并利用圖4所示的燃氣爆炸試驗系統進行了現場試驗。試驗發現:對照組試驗中爆炸超壓峰值存在一定差異，其原因可能是管廊燃氣倉內部體積較大，濃度分布并不十分均勻，但對照組試驗結果仍在試驗誤差的允許范圍內，并未改變超壓峰值的傳播和分布規律。

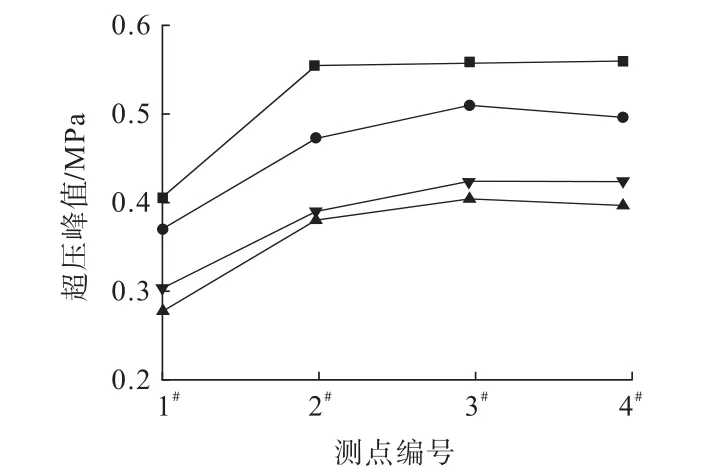
圖6 各測點的超壓峰值分布特征Fig.6 Distribution characteristics of peak overpressure at each mnoitoring points

由圖6可知:甲烷燃氣爆炸產生的壁面超壓峰值分布規律與點源爆炸特征[26]存在一定的區別，燃氣爆炸主要表現為壓力波，沒有動壓力作用的方向性，距離引爆位置最近的3#測點壁面超壓峰值在兩種甲烷濃度下僅略大于兩側的2#和4#測點，說明引爆位置對管廊內超壓峰值的分布影響有限，管廊內燃氣爆炸載荷可以近似看作時變均布載荷。根據圖5中的超壓峰值結果，在甲烷燃氣濃度為9.5%的情況下，兩次對照試驗中的最大超壓峰值出現在2#和3#測點，峰值分別達到了0.56 MPa和0.52 MPa，在濃度為10%的情況下，最大超壓峰值均位于3#測點，分別為0.41 MPa和0.45 MPa。對兩種濃度的甲烷燃氣爆炸超壓對比可以明顯看出，9.5%的甲烷燃氣濃度發生爆炸會產生更大的超壓。與受限空間內氣體爆炸超壓峰值基本相等略有區別[19]，在半自由空間中兩種濃度的爆炸超壓在管廊內傳播過程趨勢一致，在左側倉門附近均存在明顯衰減，原因是密封的木板被掀開，倉門附近的燃氣和氣壓溢出。

3 燃氣倉頂板位移值計算

3.1 模型驗證

通過Ansys/Ls-Dyna數值仿真軟件對管廊在燃氣濃度為9.5%工況下的爆炸過程進行模擬分析，采用等效內能法將燃氣爆炸荷載直接作用于管廊燃氣倉內壁上，管廊模型按照與試驗模型1∶1建立，如圖7所示。

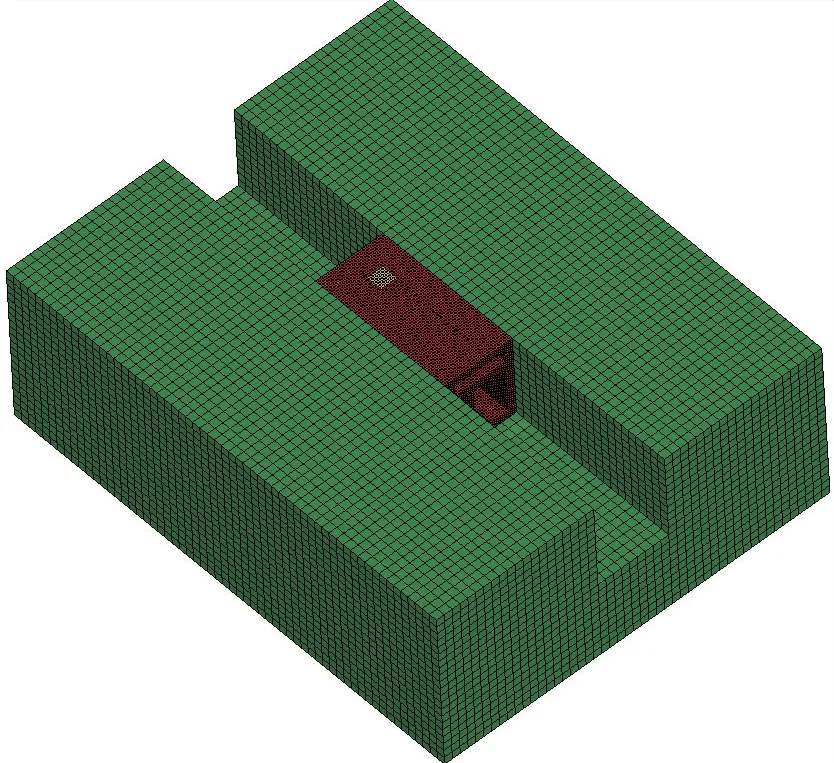
圖7 管廊數值模型Fig.7 Numerical model of pipe gallery

為了對數值模擬結果的正確性和合理性進行驗證，以管廊燃氣爆炸試驗中的空氣沖擊波壓力峰值為參考，在相同測點位置讀取數值模擬結果中的壓力峰值，并進行了對比分析，結果見表1。

由表1可知:數值模擬結果略大于試驗測得的數據，在實際試驗中由于燃氣混合不可能處于理想狀態，而且數值模擬未考慮熱力等效應，模擬結果除了在1#測點處的誤差較大外，其余3個測點的模擬值均能夠滿足精度要求。1#測點超壓峰值誤差較大的原因在于模擬過程處于理想情況，并未顧及燃氣爆炸過程中倉門被沖開、燃氣和倉內壓力在倉門附近被泄露等情況。因此，在倉門附近的1#測點模擬結果高于試驗測得的超壓峰值。

表1 模型試驗與數值模擬各測點超壓峰值Table 1 Model test and numerical simulation of the peak overpressure at each measuring point

3.2 模態分析

由于燃氣爆炸荷載直接作用于綜合管廊燃氣倉壁，因此根據式(8)對上述關系進行驗證。首先對部分參數進行求解，燃氣倉上部墻體為兩邊固支，并且中間帶空孔的混凝土板，求其固有頻率過程需解超越方程。因此，本研究采用數值模擬求該混凝土板的各階模態，計算得到該板的一階頻率并作為固有頻率，即ω=690.16 Hz，一階振型如圖8所示。

圖8 燃氣倉頂部隔墻一階振型Fig.8 First-order vibration shape of the partition wall at the top of the gas silo

3.3 最大位移響應對比

根據燃氣倉頂部混凝土墻的材料參數計算得質量 ，將各測點的超壓峰值代入式(8)，計算得到各測點處的最大位移響應見表2。

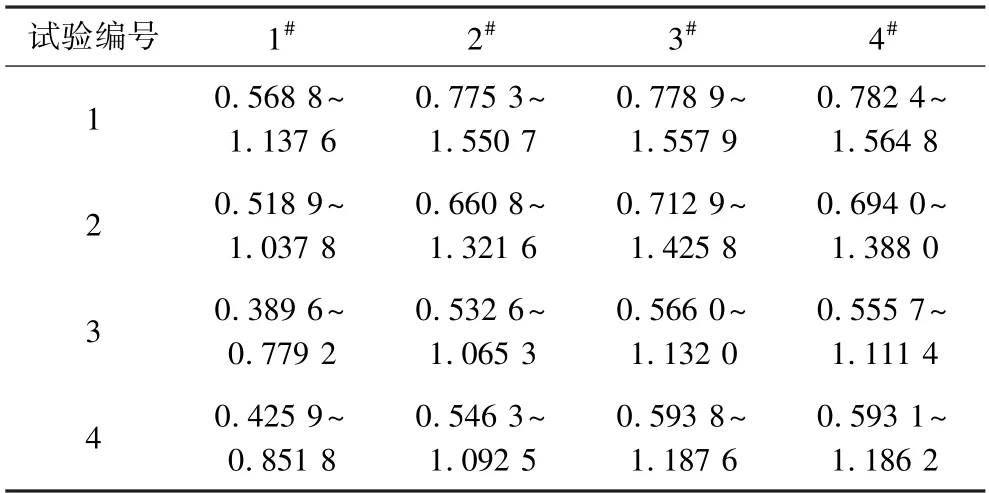
表2 各測點理論最大位移響應Table 2 Theoretical maximum displacement response of each measuring point×10-3m

根據管廊燃氣爆炸縱向位移演化云圖(圖9)分析可知，縱向位移主要發生在燃氣倉的上下混凝土板上，且位移方向由燃氣倉向外。

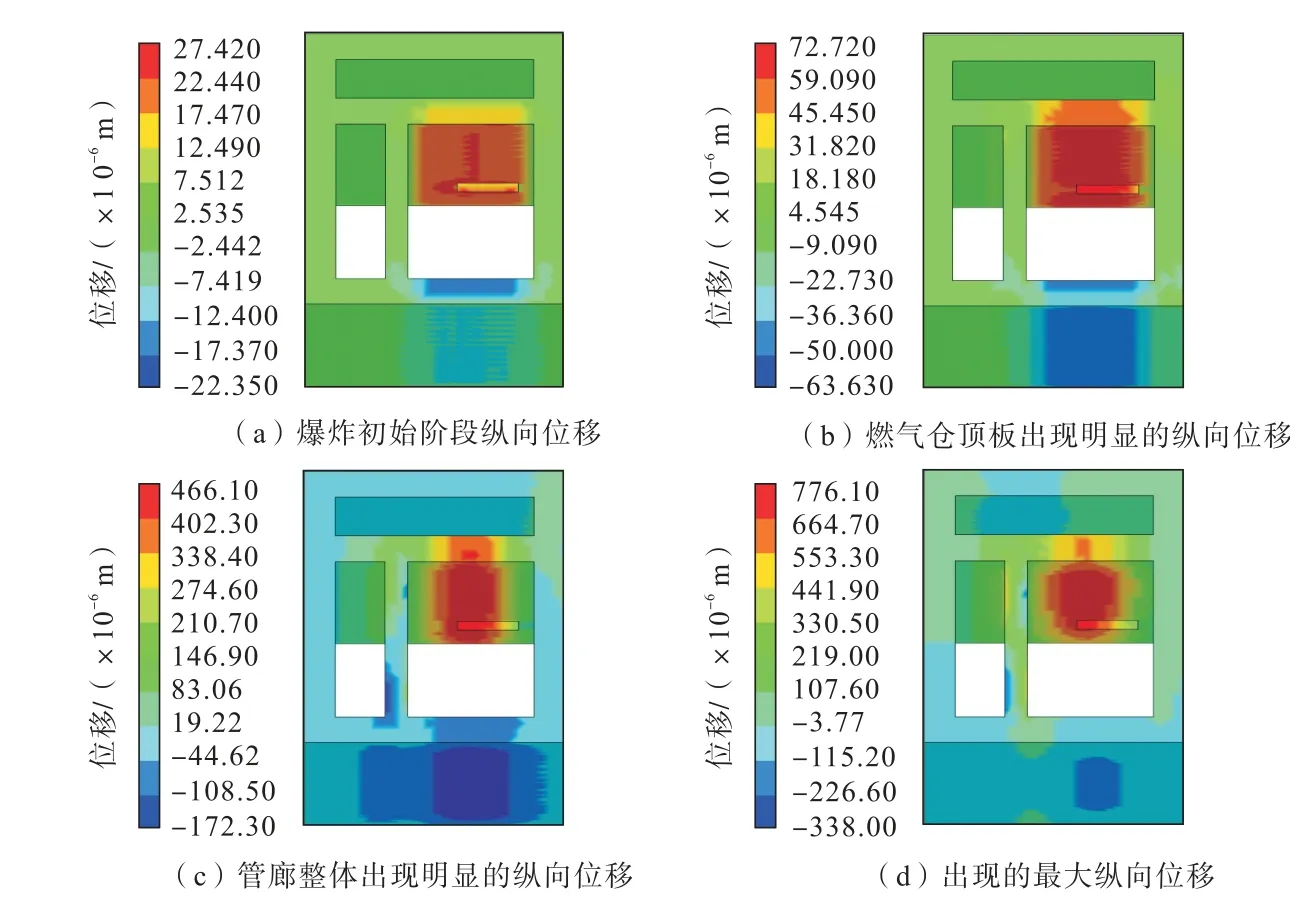
圖9 縱向位移演化云圖Fig.9 Nephogram of longitudinal displacement evolution

對數值模擬結果中的綜合管廊模型燃氣倉頂部進行取點，取點位置與壓力傳感器布置位置保持一致，獲得了如圖10所示的位移—時程曲線。分析圖10發現，除了1#測點以外各點的最大位移較為接近，均在0.75×10-3m左右。

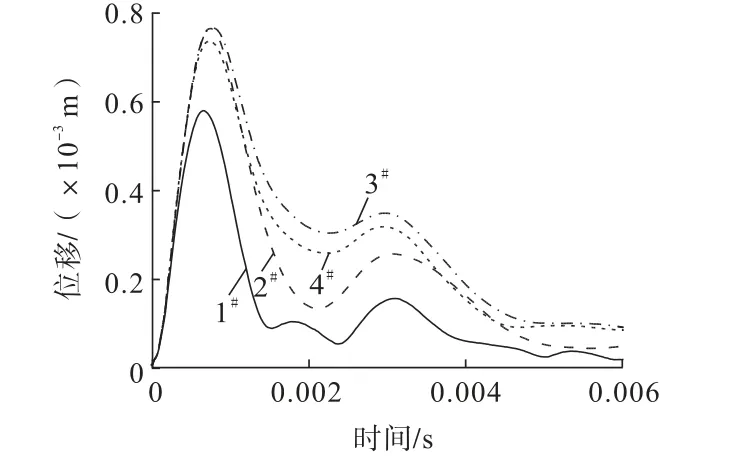
圖10 燃氣倉頂部測點位移—時程曲線Fig.10 Displacement-time history curves of monitoring points at the top of gas silo

將理論推導得出的綜合管廊燃氣倉頂部混凝土板的最大位移范圍，與數值模擬得出的最大位移響應進行校核，得到如圖11所示的位移對比圖。

圖11 理論位移與數值模擬位移對比Fig.11 Comparison of theoretical displacement and numerical simulation displacement

燃氣倉頂部混凝土板數值模擬位移與理論結果吻合度高，在各測點采集到的最大位移全部位于理論最大位移范圍內，且數值模擬位移響應變化趨勢與試驗結果一致，在1#測點處的最大位移均略小于其余測點。

4 結 論

針對甲烷氣體爆炸壓力加載較慢的特點，對管廊在燃氣爆炸荷載作用下的動力響應進行了理論分析，并開展了燃氣9.5%和10%兩種濃度在管廊模型中的氣體爆炸試驗，綜合理論推導和試驗結果，得到以下結論:

(1)模型試驗條件下，甲烷燃氣爆炸超壓—時程曲線呈單峰值狀，超壓升壓時長500～700 ms，超壓作用總時長達到1 500 ms左右，燃氣爆炸超壓作用時間與模型大小存在直接關系。

(2)甲烷燃氣爆炸超壓在管廊燃氣倉內壁各測點的作用時程曲線大致相同，各處超壓峰值基本相等，對管廊燃氣倉壁面的作用可以近似看作時變均布荷載。

(3)推導得到最大位移響應計算公式，并經過了試驗和數值模擬結果的驗證，適用于燃氣爆炸載荷作用下管廊的動力響應分析。