借助整體思想 打破常規思維

西華師范大學 林 芹 陳豫眉

1 引言

整體思想作為數學解題中的一個重要思想，旨在從已有問題的整體性質出發，認真觀察問題的整體結構，并對其進行恰當地分析與改造，把握住問題的整體結構特征，運用“集成”的眼光，將其中的某部分看成一個整體，挖掘式子或圖形間的內在聯系，再對它們進行有目的、有意識地整體處理[1]，使原有式子或圖形的結構更加清晰明了，容易解決.而這種以整體的眼光看待問題、解決問題的方法，貫穿于初中數學解題的多個方面.因此，筆者將結合實例圍繞解題過程中蘊含的整體思想，挖掘其內含的解題策略，以期幫助學生了解更多的解題方法，培養學生的整體意識，提升學生的數學思維的敏捷性、概括性與靈活性.

2 整體思想在方程與不等式中的應用

2.1 在解方程(組)中的應用

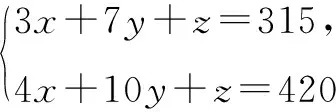
接著，運用整體思想將含有多個未知數的x+3y和x+y+z分別看成一個整體，再利用常規解法求得x+y+z的值.

從上述解方程(組)問題中不難發現，整體的實質就是一個轉化過程，旨在將陌生的數學問題轉化為熟悉的數學問題，將復雜的數學問題轉化為簡單的數學問題，使問題更加容易解決.而在解決方程或方程組的問題的過程中，利用整體思想將分式方程轉化為整式方程，將高次方程轉化為低次方程.不僅能夠減少計算量，提升解題效率，還能夠培養數學創新思維和整體意識.

2.2 在不等式(組)中的應用

例2已知1≤x-y≤2，2≤x+y≤4，求4x-2y的取值范圍.

從上述不等式(組)問題中可以發現，不等式的學習是指從學生已有的等式、方程(組)中的“相等”關系到“不等”關系的過渡，是等式的延伸.因此，在求解不等式和不等式組時，我們也要大膽嘗試解方程(組)時所采用的整體思想，著眼全局，把握已知與所求問題間的關聯，找到快速解決問題的突破口.

3 整體思想在數與式中的應用

例3已知x2-3x-6=0，求2x2-6x+1的值.

分析:本題若用常規思路解決問題，我們需要先根據x2-3x-6=0求出具體x的值，再將x的值代入到方程2x2-6x+1中求解.但是，經觀察求值式子可以發現x2-3x-6=0無法輕易因式分解，那么求未知數x的值就有一定的計算難度，需要借助一元二次方程的求根公式.很顯然解題的過程變得較為繁瑣，伴隨著求根公式的引入，計算的難度有所增加，錯誤率也易增加.然而如果從式子的整體入手，認真觀察式子的整體結構特征，就能夠發現x2-3x恰好是2x2-6x的一半，即2x2-6x+1=2(x2-3x)+1，那么，可由x2-3x-6=0 變形得x2-3x=6，再將其整體代入到式子2(x2-3x)+1中，問題就迎刃而解了.

從上述代數式求值問題中，不難發現某些代數求值問題若拘泥于常規解法，則很難得到突破，易形成舉步維艱的局勢[2].但整體思想的運用，使我們快速且準確地找尋到問題突破的關鍵，讓問題的解決變得更加簡單明了.

4 整體思想在幾何與圖形中的應用

例4如圖1所示，五邊形ABCDE中，AB∥CD，∠HAB，∠GEA，∠EDF分別是∠BAE，∠AED，∠EDC的鄰補角，求∠HAB+∠GEA+∠EDF的值.

圖1

分析：本題若從常規思路解決問題，需要分別求∠HAB，∠GEA，∠EDF的值，再進行求和計算.觀察題干，我們可以發現單從現有條件無法分別求出三個角的具體度數.但是，倘若我們運用整體的思想，將∠HAB+∠GEA+∠EDF看成一個整體，問題便迎刃而解.首先，根據多邊形內角和公式，求得五邊形的內角和為540°.又因AB∥CD，可知∠B+∠C=180°.而∠HAB+∠GEA+∠EDF+∠BAE+∠AED+∠EDC=180°×3=540°，其中∠BAE+∠AED+∠EDC=540°-180°=360°，我們將∠HAB+∠GEA+∠EDF看成一個整體，因此可得∠HAB+∠GEA+∠EDF=540°-(∠BAE+∠AED+∠EDC)=180°.

由此可知，在求解某些幾何與圖形的問題時，不應執拗于計算出其中某部分具體的值，而應當用“集成”的眼光去看待這些圖形，嘗試著將部分圖形看成一個整體，建立起局部與整體的聯系.另辟蹊徑將原本不規則的圖形變成規則圖形，為原本看似無關的部分建立起整體聯系，力求更加快速、簡單地解決問題.

5 整體思想在函數與圖象中的應用

例5已知y+m與x-n成正比例(其中m，n是常數)，求證:y是x的一次函數.

分析:本題需先將y+m和x-n當作一個整體，設y+m=k(x-n)，其中k為不等于零的常數.整理，得y=kx-(kn+m).由于k≠0，并且k，-(kn+m)都為常數，故證得y是x的一次函數.

6 總結

總而言之，解題的目的在于鍛煉思維與提升能力.而整體思想作為數學解題思想中的重要組成部分，在數與式子、方程與不等式、圖形與幾何、函數與圖象等問題的解決中，都發揮著重要的作用.整體思想的理解與掌握，不僅能夠幫助學生簡便快捷地解決問題，還能夠在整體解決問題的過程中提升創造性思維.因此，教師在教學中不僅要教會學生如何解決這類問題，更應該引導學生樂于總結，勤于反思，在解決問題的過程中能夠挖掘問題中蘊含的理論精華，感受其內含的數學思想.以期學生在今后的學習過程中，能夠自主地運用數學的整體思想走出困境，達到事半功倍的效果.