400 km/h高速鐵路橋梁豎向剛度限值研究
向活躍, 陳緒黎, 張 玲, 李永樂
(1. 西南交通大學 土木工程學院,成都 610031; 2. 中鐵第四勘察設計院集團有限公司,武漢 430063)
隨著我國鐵路行業的高速發展,高速鐵路里程顯著增加,截至2020年底達3.79萬km。響應“客運高速、貨運重載”的運輸發展方向,建設運營設計400 km/h及以上的高速鐵路已提上日程[1-2]。車速增加必然會對橋梁設計提出更高要求,豎向剛度限值作為控制橋梁變形的重要指標,對列車運營安全性和乘坐舒適性有顯著影響,現行TB 10002—2017《鐵路橋涵設計規范》[3](后文簡稱鐵路橋規)適用于350 km/h及以下車速,研究400 km/h高速鐵路橋梁的剛度限值有重要研究意義。
高速列車通過橋梁會激起橋梁振動,橋梁振動又會反作用于車輛,車速增加時,車橋動力響應也會進一步增加,過低的橋梁剛度可能會導致橋面坡度超限、乘坐不適、甚至列車脫軌等現象發生[4],所以各國規范對豎向剛度限值做出嚴格要求,具有代表性的有日本[5]、UIC[6]和中國等相關規范。剛度限值通常可采用橋梁豎向撓度限值表示,當主梁豎向撓度較大時支座轉角通常也較大,線路不再平順連續,所以鐵路橋規對梁端豎向轉角也進行了限值規定[7],本文將同時考慮橋梁豎向撓度限值和梁端豎向轉角限值的影響。
沈銳利[8]在不考慮橋梁振動情況下,使用整車模型計算車輛通過不同跨度的單跨簡支梁和多跨連續布置的等跨度簡支梁橋的最大撓跨比,對高速鐵路橋梁的剛度限值有一定參考意義。高巖等[9]采用23自由度車輛模型,通過改變橋梁截面剛度,基于車橋耦合振動分析方法,計算7種中小跨度單跨和等跨度多跨簡支梁橋的豎向剛度限值。翟婉明等[10]采用國產高速列車和32 m簡支梁橋進行動力相互作用分析,通過調整橋梁截面慣性矩改變橋梁豎向剛度,研究橋梁剛度較小時列車—軌道—橋梁耦合系統的動力特性變化。李奇等[11]考慮橋梁徐變、溫度、橋墩沉降等影響下的靜態變位,采用CRH3高速列車和不同跨度的簡支梁橋進行車橋耦合振動分析,改變橋梁剛度得到車輛安全性、舒適性指標,計算車輛響應指標達到限值時在設計活載作用下的撓跨比,即為橋梁豎向剛度限值。
從已有研究和現行設計規范發現,不同車速條件下,不同跨度橋梁的豎向剛度要求差異大,且多針對車速350 km/h及以下高速鐵路,對400 km/h高速鐵路橋梁豎向剛度研究較少。
本文基于鐵路橋規數據分析400 km/h高速鐵路橋梁的剛度限值;然后,按規范中跨度劃分范圍選取3種跨度橋梁,采用時速400 km/h高速列車參數,基于車橋耦合振動分析方法,并考慮車速、車輛載重、車輛編組和橋型等因素的影響,對橋梁豎向撓度限值和梁端豎向轉角限值進行分析;最后得到400 km/h高速鐵路橋梁豎向剛度限值的參考值。
1 基于現行規范數據的分析
根據鐵路橋規和文獻[12]研究,豎向剛度限值指標可按豎向撓度和梁端豎向轉角兩部分考慮。鐵路橋規中按不同車速及跨度條件給出豎向撓度限值,設計時在ZK荷載作用下梁體豎向撓度限值規定,如表1所示。表1中L為橋梁跨度,三跨及以上一聯的連續梁撓度限值需按表中數值1.1倍取用。根據表1中3種跨度范圍橋梁在車速250 km/h,300 km/h,350 km/h的豎向撓度,按二次項擬合得到車速400 km/h的豎向撓度,擬合曲線如圖1所示。
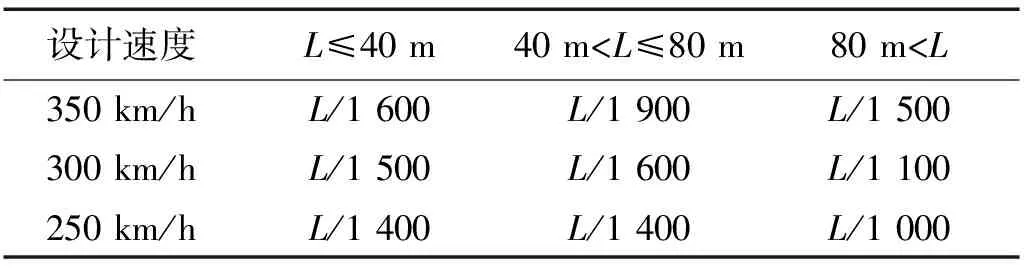
表1 梁體豎向撓度限值Tab.1 The limit of vertical deflection of beam
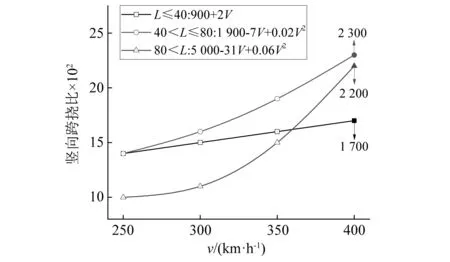
圖1 豎向撓度擬合曲線Fig.1 Fitting curve of vertical span deflection ratio
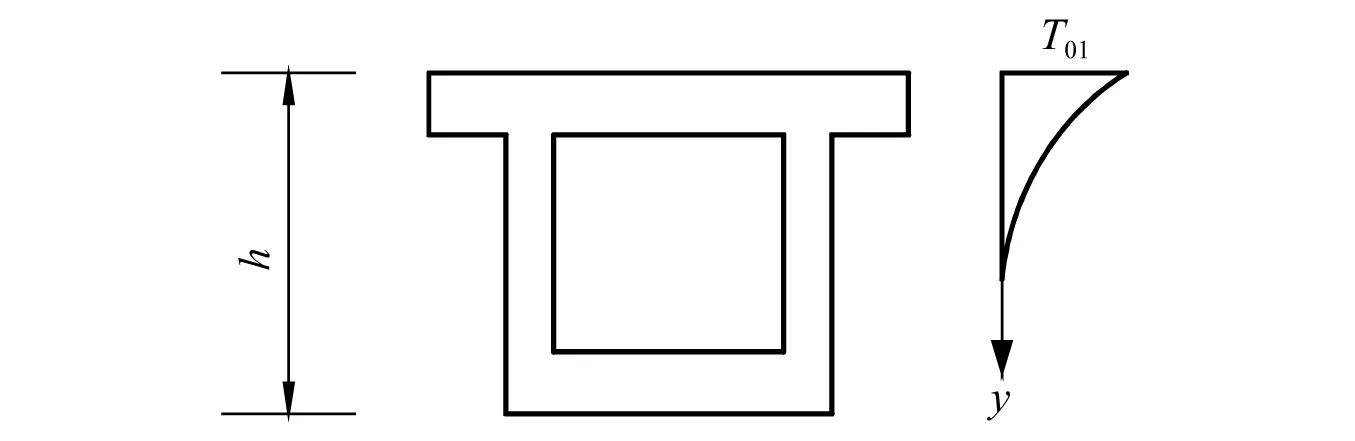
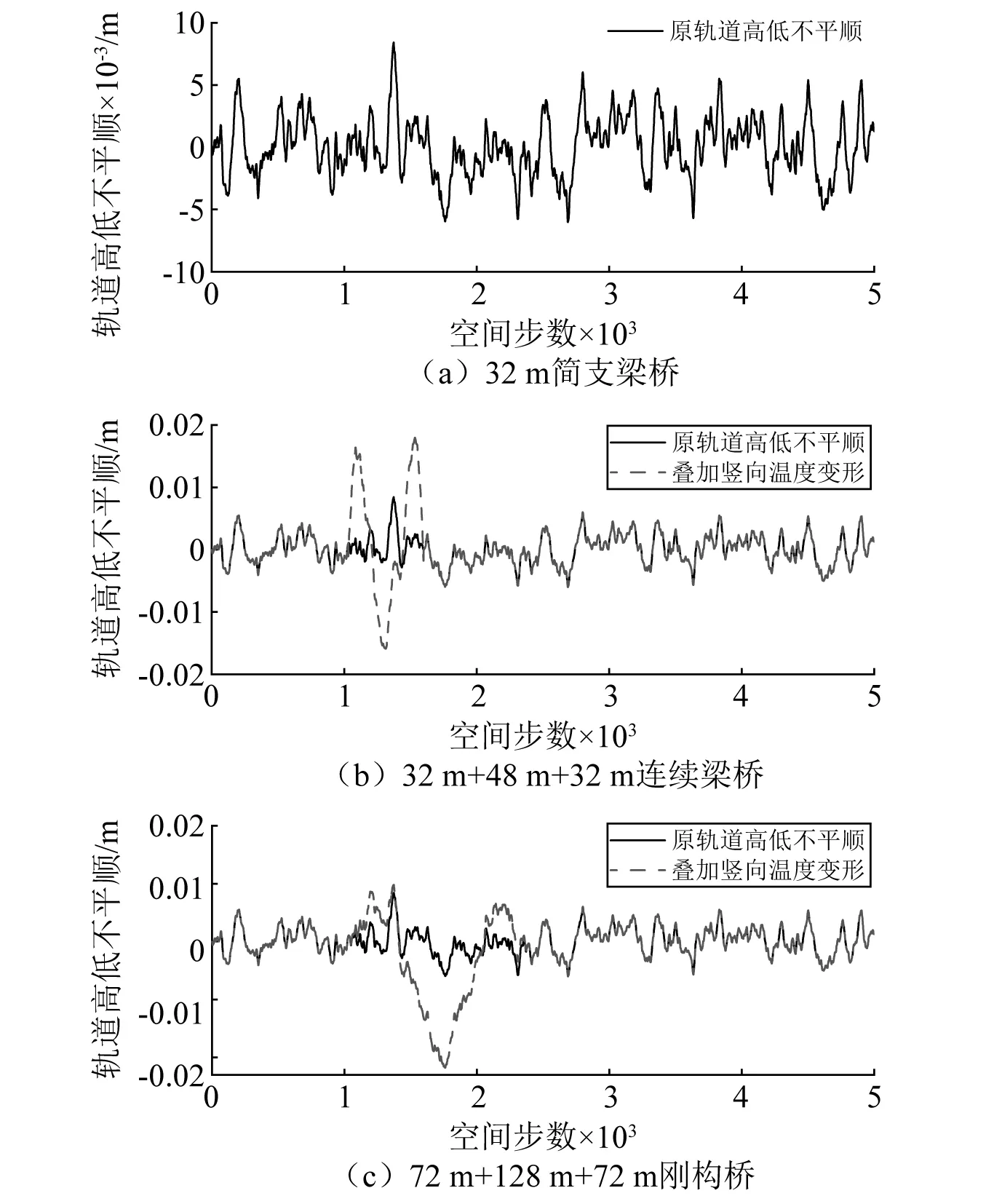
由圖1可見,當車速為400 km/h時,L≤40 m豎向撓度限值為L/1 700,40 m 按鐵路橋規要求,根據梁端懸出長度對梁端豎向轉角進行取值,無需考慮車速、橋型和跨度條件等因素的影響。 我國尚未建成400 km/h高速鐵路線路,無法通過試驗獲得線路中橋梁的剛度指標,為進一步確定400 km/h 高速鐵路橋梁的豎向剛度限值,可采用車-橋耦合振動分析方法進行研究。 時速400 km/h高速列車與時速350 km/h高速列車的動力學參數有一定差異,但車輛結構基本相似,仍可看作兩系懸掛質量彈簧阻尼車[13],如圖2所示。每節車輛由1個車體、2個轉向架和4個輪對共7部分剛體以及彈簧、阻尼元件組成,車體和轉向架考慮5個自由度,輪對僅考慮橫移和搖頭2個自由度,整車為23自由度。根據達朗貝爾原理,可得車輛的運動方程 (1) 時速400 km/h高速列車,頭車長28.064 m,中間車長25.650 m。研究中,車輛編組考慮8車和16車兩種編組,車輛載重考慮空載和滿載兩種情況,共有8編組空載、8車編組滿載、16車編組空載和16編組滿載4種車輛工況;車速考慮350 km/h和400 km/h。 圖2 23自由度車輛模型Fig.2 23 degree of freedom train model 分析中,橋梁均為無砟軌道預應力混凝土雙線橋,橋梁跨中截面形式如圖3所示。在有限元軟件中使用Beam4梁單元進行建模,經動力特性分析,得到橋梁自振頻率、總體質量矩陣和總體剛度矩陣等信息,橋梁阻尼比為0.02,由Rayleigh阻尼計算公式可計算橋梁總體阻尼矩陣。橋梁子系統的運動方程[14]可寫作 (2) 圖3 橋梁跨中截面示意圖Fig.3 Schematic diagram of bridge mid-span section 分析中,采用15跨32 m簡支梁橋、32 m+48 m+32 m連續梁橋和72 m+128 m+72 m剛構橋進行400 km/h高速鐵路橋梁豎向剛度限值研究。簡支梁橋和連續梁橋主梁采用C50混凝土,剛構橋主梁采用C55混凝土。簡支梁橋和連續梁橋橋墩采用C40混凝土,剛構橋邊墩和中墩分別采用C35和C40混凝土,橋墩均為空心墩,墩高均為50 m,文獻[15]研究表明墩高對梁體豎向動力響應影響較小。3種橋梁的豎向基頻和跨中截面慣性矩信息,如表2所示。 表2 橋梁模型結構信息Tab.2 Structural information of bridge model 根據幾何相容條件和靜力平衡條件[16],車輛子系統運動方程和橋梁子系統運動方程進行分離迭代,輪軌接觸采用德國低干擾譜,空間步長取為0.2 m,并使用AR法[17]生成軌道不平順樣本。借助自主研發軟件Bansys進行車橋耦合振動分析。 計算時分為兩步:第一步基于車橋耦合振動分析方法,計算不同橋梁豎向剛度時的車輛響應; 第二步將各剛度的橋梁模型按規范條件進行加載計算豎向撓度和梁端豎向轉角,車輛響應超限時對應的橋梁豎向剛度即為豎向剛度限值。 為方便設計,提出的剛度限值仍需采用已有規范的加載形式。雙線橋梁需在結構最不利位置加載100%的ZK荷載,加載時列車荷載圖式可按影響線長度任意截取,在同符號影響線區段加載ZK荷載,異符號影響線區段大于15 m時加載10 kN/m,小于15 m時不進行加載。32 m簡支梁橋計算豎向剛度和梁端轉角的荷載加載圖示相同,如圖4(a)所示;根據32 m+48 m+32 m連續梁橋和72 m+128 m+72 m剛構橋的中跨跨中彎矩影響線,豎向剛度計算加載圖示如圖4(b)和圖4(c)所示,根據邊跨跨中彎矩影響線,梁端轉角計算加載圖示如圖5所示。 圖4 豎向撓度限值加載示意圖Fig.4 Loading diagram of vertical deflection limit 圖5 梁端轉角限值加載示意圖Fig.5 Loading diagram of girder-end rotation limit 按鐵路橋規要求,對于連續梁橋等超靜定結構,計算豎向剛度時需考慮溫度變形的影響。溫度變形包含均勻溫差和日照溫差兩部分變形,形式和大小可參考TB 10092—2017《鐵路橋涵混凝土結構設計規范》[18]。均勻溫差從合龍時的溫度算起,考慮整體升降溫 20 ℃。日照溫差為指數形式,如圖6所示,沿箱梁高度方向上的溫度大小計算如式(3)所示 Ty=T01e-ay (3) 式中:Ty為計算點y處的溫差;T01為箱梁梁高方向溫差,考慮鋪設無砟軌道后,梯度升溫時取為10 ℃,梯度降溫時取為-5 ℃;a在升溫時取為5 m-1,降溫時取為14 m-1。 圖6 箱梁豎向溫差分布圖Fig.6 Vertical temperature difference distribution of box girder 由于進行車橋耦合振動計算時,通過降低截面慣性矩的方式實現不同橋梁剛度,梁剛度不同時截面尺寸應有所區別,為簡化計算,溫度效應計算中仍采用原尺寸,使用MIDAS Civil軟件計算各剛度橋梁的溫度變形。 計算橋梁豎向剛度時,通過降低橋梁模型豎向慣性矩,并保證其他參數均不變的條件下,基于車橋耦合振動分析計算車輛動力響應;同時,按鐵路橋規要求對降低豎向慣性矩的相應橋梁模型在最不利位置進行加載得到橋梁變形,從而建立車輛動力響應與橋梁豎向剛度之間的關系。車輛響應在限值處的橋梁豎向剛度,即為橋梁結構設計時豎向剛度限值,具體步驟如下。 步驟1豎向撓度限值 ①按1/5、1/8、1/10、1/12、1/14、1/16、1/18乘以橋梁豎向慣性矩,降低橋梁豎向剛度,計算不同剛度倍數下橋梁的豎向溫度變形; ②將各剛度倍數下的橋梁豎向溫度變形按0.2 m的間隔進行插值,疊加至軌道高低不平順,進行車橋耦合振動分析,獲得車輛響應。以剛度下降1/18倍為例,3種橋梁進行車橋耦合計算時的軌道高度不平順如圖7所示,32 m簡支梁橋撓度限值不考慮溫度作用,軌道高低不平順中不疊加豎向溫度變形。 圖7 軌道高低不平順Fig.7 Track vertical irregularity ③各剛度倍數下,32 m簡支梁橋、32 m+48 m+32 m連續梁橋、72 m+128 m+72 m剛構橋分別按圖4(a)、圖4(b)、圖4(c)加載ZK荷載,得到橋梁在ZK荷載作用下的最大豎向撓度,將各橋梁ZK荷載和0.5倍溫度引起的豎向撓度之和與0.63倍ZK荷載和全部溫度引起的豎向撓度之和進行比較,并取兩者中的大值最為橋梁豎向撓度。 ④將各剛度倍數下的車輛響應和橋梁豎向撓度一一對應,插值計算車輛響應限值時的橋梁豎向撓度限值,并與鐵路橋規的豎向撓度限值進行比較,判斷現行鐵路橋規的豎向撓度限值對400 km/h高速鐵路橋梁的適應性。 步驟2梁端豎向轉角限值 ①按1/5、1/8、1/10、1/12、1/14、1/16、1/18乘以橋梁豎向慣性矩,從而降低橋梁豎向剛度,軌道高低不平順中不考慮溫度變形,進行車橋耦合振動分析,獲得車輛響應。 ②各剛度倍數下,32 m簡支梁橋按圖4(a)、32 m+48 m+32 m連續梁橋按圖5(a)、72 m+128 m+72 m剛構橋圖5(b)加載ZK荷載,得到橋梁最大梁端轉角。 ③將各剛度倍數下的車輛響應和橋梁最大梁端轉角進行對應,插值計算車輛響應限值時的梁端豎向轉角限值,并與現行規范的梁端豎向轉角限值進行比較,判斷現行鐵路橋規的轉角限值是否適用于400 km/h高速鐵路橋梁。 為保證列車運營安全性和乘坐舒適性,鐵路橋規對車輛的安全性和舒適性作出了相應的規定,其中車輛限值指標適用于車速350 km/h及以下工況。加速度指標反映人體舒適性,其限值要求不應隨車速的增加而改變,車輛安全性指標在車速400 km/h如何取值有待進一步研究。本文的車橋耦合振動分析表明,車輛豎向加速度最早達到規范限值(1.3 m/s2),歐洲規范和日本規范也表明控制橋梁剛度是主要是為滿足乘坐舒適度。考慮到車輛舒適性指標通常較安全性指標更加嚴格,因此以車輛的加速度響應指標進行后續分析。 通過車橋耦合振動分析,計算得到3種橋梁的豎向撓度限值如圖8所示。由圖8可見,當車速為400 km/h時,32 m簡支梁橋的豎向撓度限值為L/882,大于規范限值L/1 700;32 m+48 m+32 m連續梁橋豎向撓度限值為L/750,大于規范限值L/2 090; 72 m+128 m+72 m剛構橋的豎向撓度限值為L/1 584,大于規范限值L/2 000;當車速為350 km/h時,計算得到的豎向撓度限值也均大于規范限值。車速400 km/h較車速350 km/h計算得到的豎向撓度限值變小,約減少8%~18%,車速更高時豎向撓度限值要求更加嚴格。當橋梁豎向剛度下降到一定程度時,車輛豎向加速度變化加快。 圖8 3種橋梁豎向撓度限值Fig.8 The limit of vertical deflection of three kinds of bridges 車橋耦合振動分析中,車輛響應受隨機軌道幾何不平順的影響,會導致車輛響應會有一定的差異。同時,軌道幾何不平順在不同位置與溫度變形疊加時也會導致車輛響應的計算結果有一定的差異。部分研究是通過乘以安全系數的方式來考慮隨機性的影響[19]。從高速列車響應隨機性的研究結果看,受軌道幾何不平順隨機性的影響,車輛豎向加速度在超越概率為10-4時的數值與最小值相差約一倍,其計算中采用的是32 m簡支梁橋[20]。對比圖8(a)計算結果可見,當車速為350 km/h和400 km/h時,計算的撓度限值在考慮2.0的安全系數后,與現行規范值和外推值均較為吻合。在其他兩種橋梁跨度中,兩種車速下計算的豎向撓度限值均大于現行規范值及其外推值,表明規范對豎向撓度限值要求更加嚴格,且具有合理的安全儲備。 考慮規范規定的連續性,所以400 km/h高速鐵路橋梁豎向撓度限值可采用現行規范由車速250 km/h,300 km/h,350 km/h擬合外推得到的400 km/h的豎向撓度限值,即,L≤40 m豎向撓度限值取為L/1 700,40 m 規范對不同梁端懸出長度的高速鐵路橋梁做出梁端轉角限值規定,32 m簡支梁橋、32 m+48 m+32 m連續梁橋和72 m+128 m+72 m剛構橋的梁端懸出長度分別為0.55 m,0.75 m和0.70 m,簡支梁橋共有15跨,可考慮橋梁與橋臺梁端豎向轉角限值θ、相鄰兩孔梁每孔梁梁端豎向轉角限值θ以及相鄰兩孔梁梁端豎向轉角限值之和θ1+θ2,連續梁橋和剛構橋只考慮橋梁和橋臺處的梁端豎向轉角限值θ,3種橋梁梁端豎向轉角限值如表3所示。 表3 梁端豎向轉角規范限值Tab.3 The limit of vertical girder-end rotation in code 通過車橋耦合振動分析,計算得到3種橋梁的梁端豎向轉角限值如圖9所示。圖9顯示,當車速為400 km/h時,32 m簡支梁橋橋梁與橋臺梁端豎向轉角為2.71‰ rad,相鄰兩孔梁每孔梁梁端豎向轉角為3.47‰ rad,均大于規范限值1.5‰ rad,相鄰兩孔梁梁端豎向轉角之和為6.17‰ rad,大于規范限值3‰ rad;32 m+48 m+32 m連續梁橋、72 m+128 m+72 m剛構橋橋梁與橋臺梁端轉角為2.05‰ rad,1.37‰ rad,均大于規范限值1‰ rad。車速400 km/h較350 km/h的計算得到的梁端轉角限值變小,減少約16%~20%,梁端豎向轉角限值要求更加嚴格。鐵路橋規也指出無砟軌道大跨度橋梁的梁端轉角限值往往成為梁體剛度設計控制指標,本文中3種跨度橋梁隨跨度增加而梁端豎向轉角限值減小,這與鐵路橋規的結論一致。 圖9 3種橋梁梁端豎向轉角限值Fig.9 The limit of girder-end rotation of three kinds of bridges 通過比較鐵路橋規和車輛加速度限值對應的梁端豎向轉角限值,車速400 km/h計算得到的梁端豎向轉角限值較車速350 km/h減少約16%~20%,但仍大于鐵路橋規限值,有一定安全儲備,所以車速為400 km/h的高速鐵路橋梁梁端豎向轉角限值仍可采用鐵路橋規限值,即梁端懸出長度不超過0.55 m時,橋臺與橋梁之間梁端豎向轉角限值為1.5‰ rad,相鄰兩孔梁梁端豎向轉角之和限值為3‰ rad;梁端懸出長度不超過0.75 m時,橋臺與橋梁之間梁端豎向轉角限值為1‰ rad,相鄰兩孔梁梁端豎向轉角之和限值為2‰ rad。 利用鐵路橋規數據外推和車橋耦合振動的方法研究400 km/h高速鐵路橋梁的豎向撓度限值與梁端豎向轉角限值,分析相應的豎向剛度建議值,得出以下結論: (1) 車橋耦合振動計算值較規范數據外推值大,豎向撓度限值的要求隨車速的增加而提高,考慮隨機性及規范規定連續性的影響,建議400 km/h高速鐵路橋梁跨度L≤40 m,豎向撓度限值為L/1 700,40 m (2) 基于車橋耦合振動分析,車速400 km/h時的梁端豎向轉角較350 km/h減少約16%~20%,但仍然大于鐵路橋規梁端豎向轉角限值,有一定安全儲備,建議400 km/h高速鐵路橋梁梁端豎向轉角限值仍可根據梁端懸出長度按現行規范限值取值。2 車橋耦合模型
2.1 車輛模型
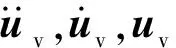

2.2 橋梁模型
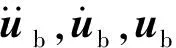
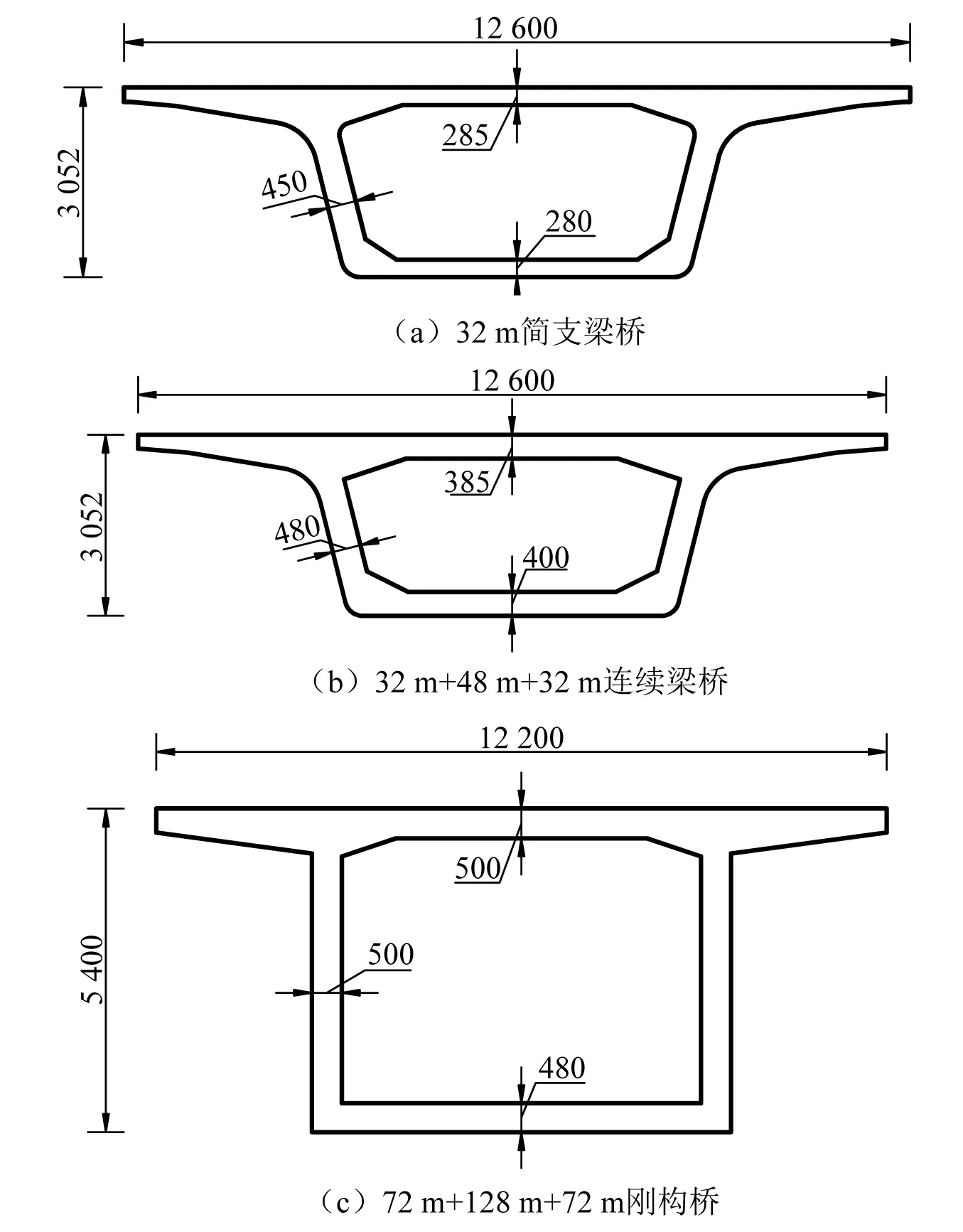
3 豎向剛度限值的計算方法
3.1 按規范條件加載
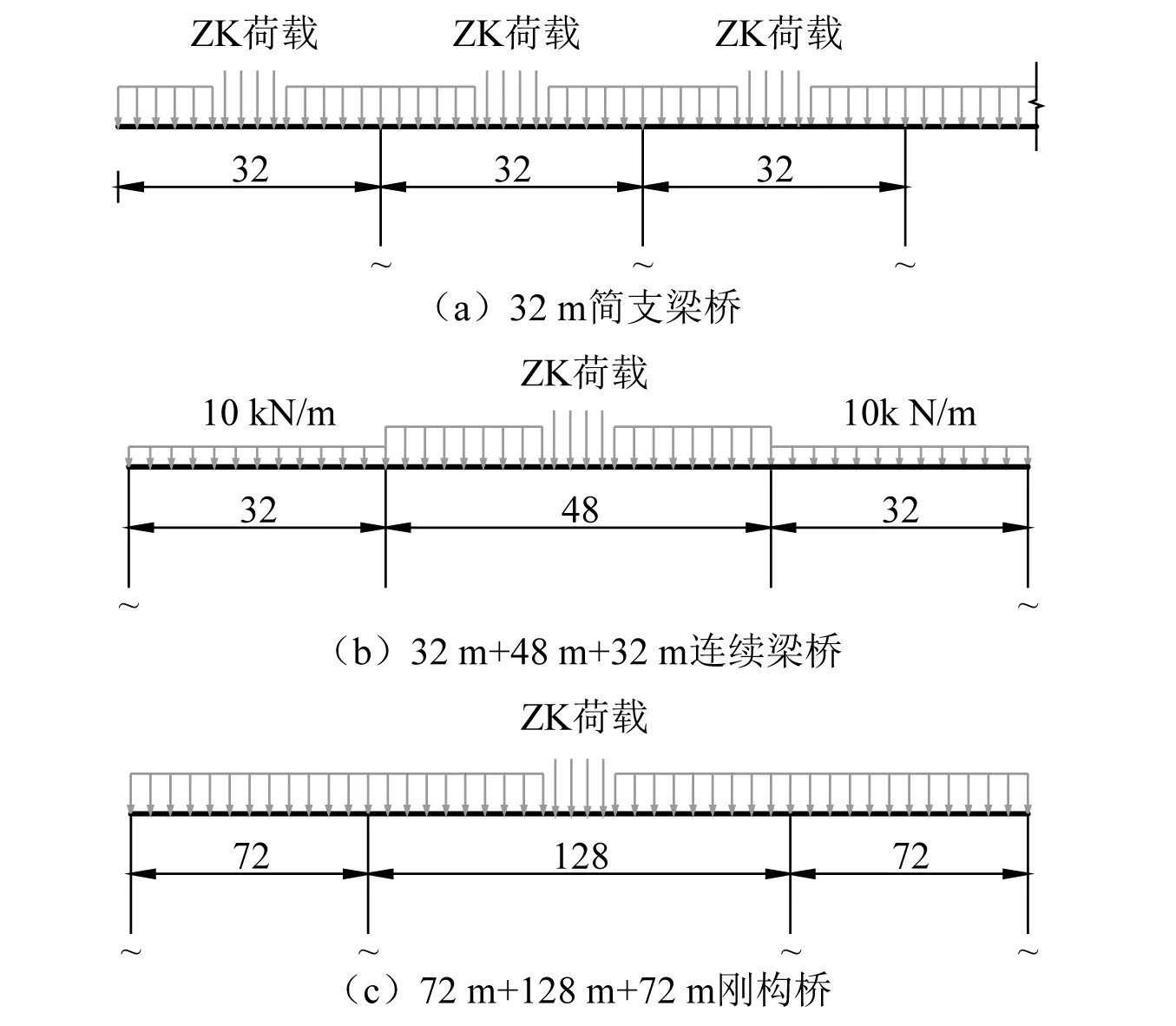
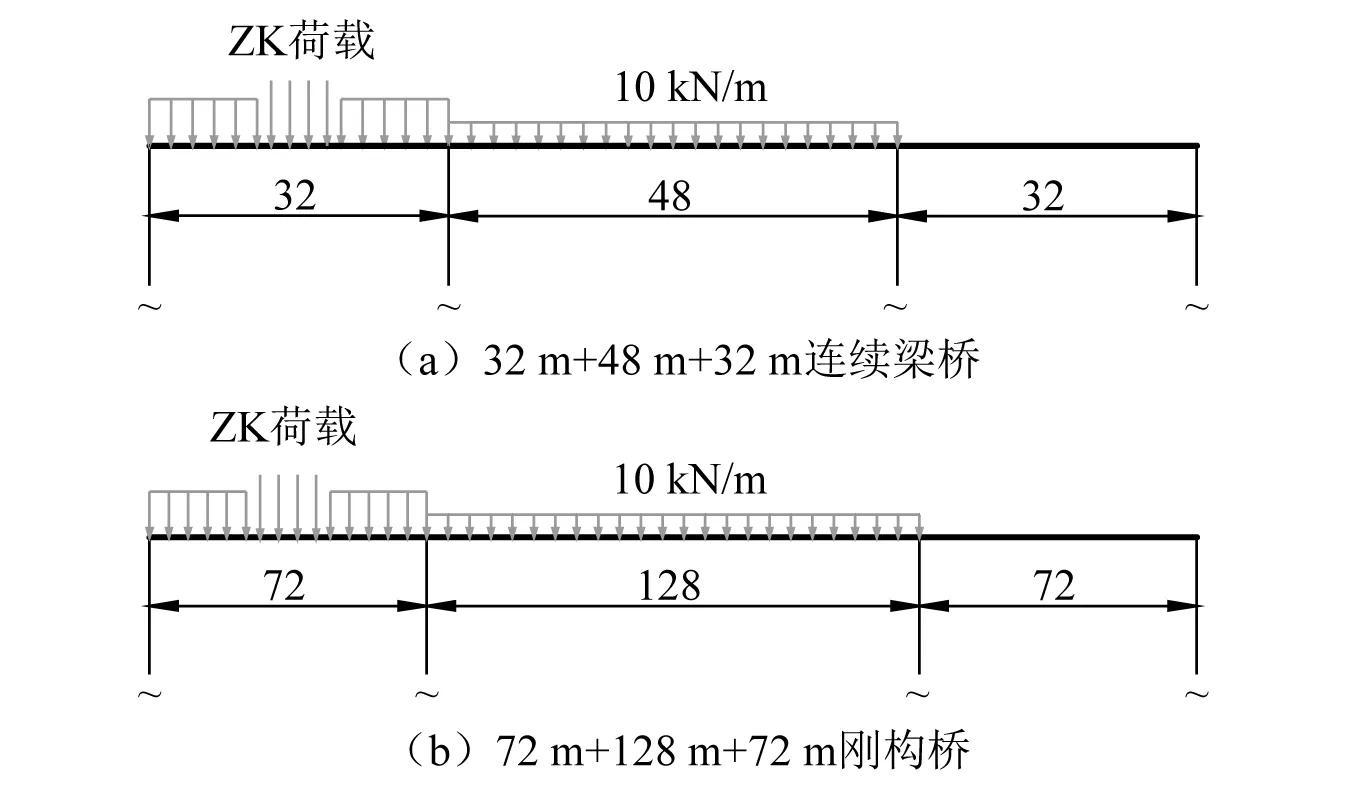
3.2 計算步驟
4 結果分析
4.1 豎向撓度限值

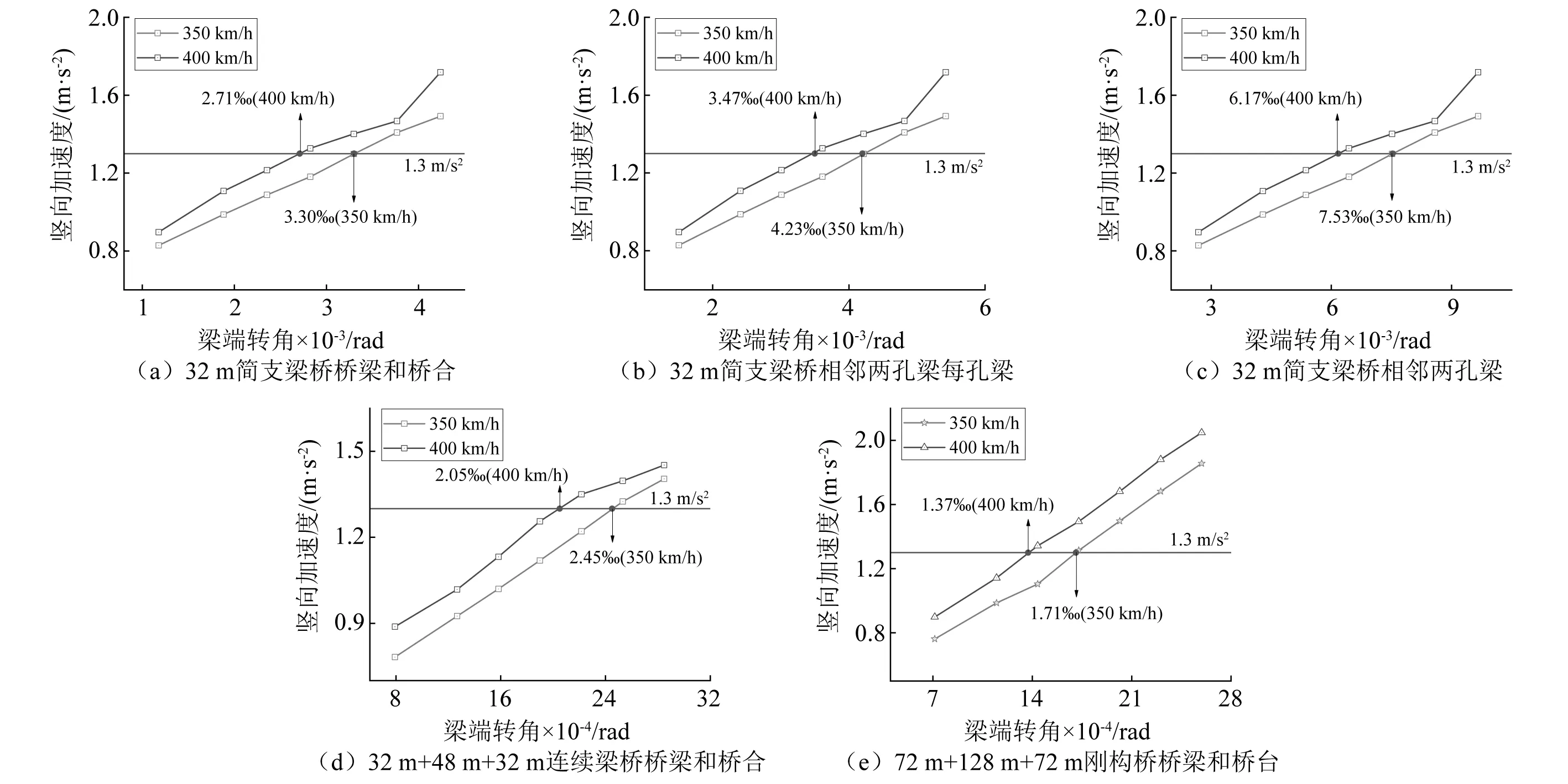
4.2 梁端轉角限值

5 結 論

