基于AUKF的鋰離子電池SOC估計方法*

王 萍，弓清瑞，程 澤，張吉昂

（天津大學電氣自動化與信息工程學院，天津 300072）

前言

鋰電池作為一種清潔能源，以其能量密度高、體積小、壽命長等優點，被廣泛應用于電動汽車和電力系 統 等 諸 多 領 域。 電 池 管 理 系 統（battery management system，BMS）可以實現對電池的科學評估和風險預警，從而保證電池的穩定運行。電池荷電狀態（state of charge，SOC）直接反映了電池的剩余電量，它的準確估計是BMS 運維的關鍵環節。然而SOC 并不能直接測量，只能通過電池的外部可測變量，結合數學算法來推斷。

目前SOC 的估計方法主要有直接測量法、數據驅動法和基于自適應濾波器的方法。

直接測量法包括安時積分法和開路電壓法。安時積分法是通過對放電過程中電流隨時間積分來獲得SOC。該方法有簡單易用的優點，但十分依賴于SOC 初值的確定，且電流的測量誤差會隨時間累積。開路電壓法是通過測量電池的開路電壓（open circuit voltage，OCV），通過查詢OCV-SOC 曲線來獲得電池SOC。但該方法須將電池離線后進行長時間靜置，因而難以用于SOC的在線估計。

數據驅動法是使用機器學習的算法建立電池外部可測變量如電壓、電流和溫度等參數與SOC 的映射關系。機器學習方法主要包括統計機器學習方法和神經網絡的方法。其中，后者有更靈活的內部結構，對非線性關系的表達能力也更強，應用也更廣泛。這類方法無須分析電池復雜的電化學反應，但計算量較大，且十分依賴于訓練集的有效可靠。

基于自適應濾波的方法須建立等效電路模型，再結合濾波算法來實現SOC 的閉環估計。如文獻［11］中使用2 階RC 模型對鋰電池進行建模，并結合模糊自適應卡爾曼濾波器來實現對SOC 的實時估計。常用的等效電路模型有PNGV 模型和RC 模型等。常用的濾波算法有觀測器、粒子濾波器、卡爾曼濾波器等，其中卡爾曼濾波器最為常用，有著許多優秀的變型，如擴展卡爾曼濾波器、自適應擴展卡爾曼濾波器和無跡卡爾曼濾波器等。這類方法可以矯正SOC初始值不確定造成的誤差和緩解過程中誤差積累，但對等效電路的參數較為敏感。

無跡卡爾曼濾波器（unscented Kalman filter，UKF）因其優越的性能被廣泛應用。但UKF 存在對電池模型精度和系統噪聲的要求較高，穩定性不強的問題。針對該問題，本文中引入一般性的濾波器收斂判據，從自適應調整測量噪聲、調整過程噪聲和修正卡爾曼增益的角度改進UKF，形成了基于自適應無跡卡爾曼濾波器（adaptive unscented Kalman filter，AUKF）的SOC 估計方法。本文利用測試數據和馬里蘭大學電池數據集進行了實驗，結果表明所提方法具有較快的收斂速度和較高的估計精度。

1 RC等效電路模型

RC 等效電路模型結構簡單，只需少量的參數和較低的計算成本便可完成建模，應用廣泛。本文以2階RC 模型為例，展示電池建模和SOC 估計的過程，模型結構如圖1所示，其狀態空間數學表達式為

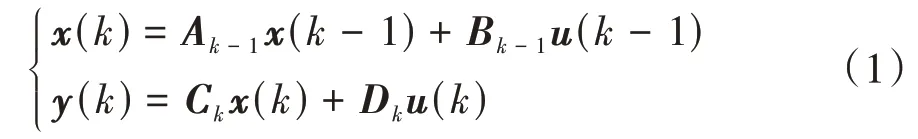
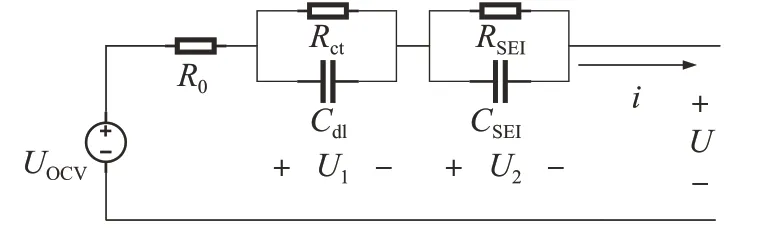
圖1 2階RC模型的結構

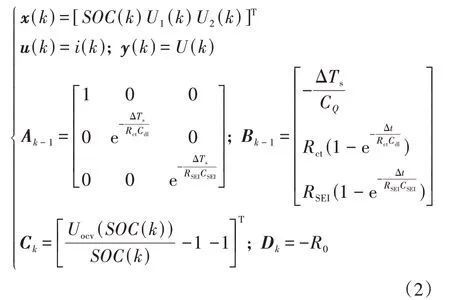
式中：表示電池端電流；代表電池端電壓；表示電池的歐姆內阻；和并聯環節表示電化學極化過程，和并聯環節表示濃度差極化過程；表示電池的開路電壓。

本文通過離線實驗對RC 模型阻容等參數進行辨識，具體包括（·）、、、、和。

2 參數辨識

2.1 CCP測試

本文的實驗對象是額定容量為3 A·h、標稱電壓為3.6 V 的18650 三元鋰離子電池。設定恒溫箱溫度為25 ℃，采用恒流脈沖（constant current pulse，CCP）測試進行參數辨識，實驗步驟如下：

①將室溫下充滿電的電池置于恒溫箱內，靜置1 h，記錄電池的開路電壓；

②以1C恒流放電3 min；

③靜置2 h，記錄電池的靜置電壓；

④重復過程②和③直至電池放空。

CCP 實驗的電壓和電流全周期和一個周期的變化曲線如圖2和圖3所示。

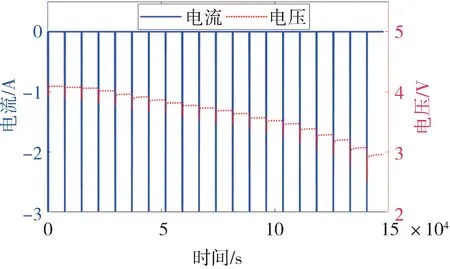
圖2 CCP測試全周期曲線圖

圖3 中A 點之前電池處于靜置狀態；在BC 段，以1C 放電3 min，電壓快速下降，SOC 下降0.05；在DE 段，電池靜置2 h，電流為0，電壓緩慢回升，并逐漸趨于穩定。

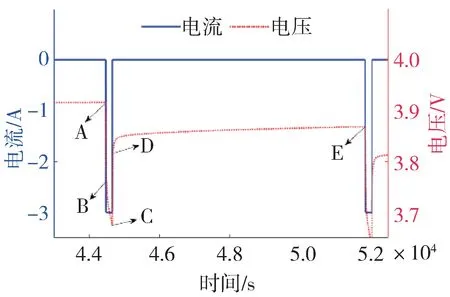
圖3 CCP測試一個周期曲線圖

2.2 OCV-SOC曲線擬合

在CCP 測試第③步中，取靜置結束時刻的E 點電壓值作為當前SOC 下的OCV 值。CCP 測試過程共得到20 個SOC-OCV 散點。本文將電化學模型Shepherd、Unnewehr 和Nerst 進行組合，得到一種較為理想的開路電壓模型，如式（3）所示，使用最小二乘法來對其進行擬合，從而得到各參數的辨識值。

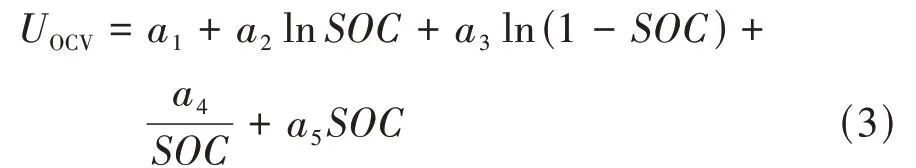
2.3 阻容參數辨識

2.3.1的辨識

分別計算通電瞬間（AB 段）和斷電瞬間（CD 段）的后，取二者的平均值作為最終值，計算式為

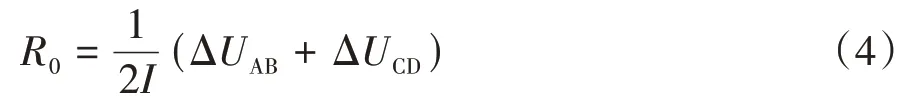
式中Δ和Δ分別為通電和斷電瞬間電壓變化的絕對值，分別對應圖3 中AB 段的電壓驟降和CD段的電壓驟升。

2.3.2、、和的辨識

DE 段可看作是RC 環節的零輸入響應。D 為起點，電容和兩端初始電壓分別為（0）和（0），這時端電壓表達式如式（5）所示。使用最小二乘法對式（5）進行擬合，可以得到（0）、（0）以及時間常數、的值。

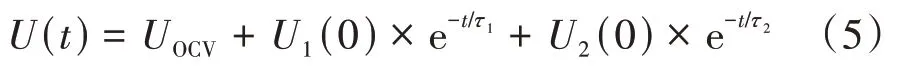
BC 段可看作RC 環節的零狀態響應。因為電容電壓不能突變，由C 點和D 點的極化電壓相等的關系可得

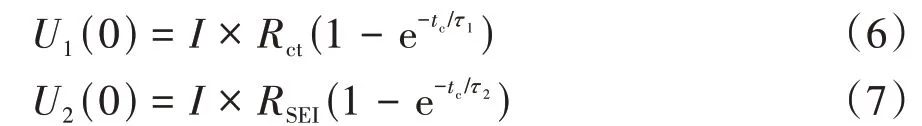
式中=3 min。

由式（6）和式（7）可計算得到和，進一步由=×的關系可得和。

RC 模型的阻容參數會隨SOC 的變化產生波動，使用線性插值法來擬合這種波動，即

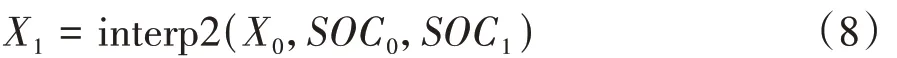
式中：=｛0.95，0.9，...，0｝；X為對應的參數取值序列；為某個實際的SOC 值。Interp2 表示2 維線性插值運算，即在與距離最近的兩個參考點之間建立線性模型，將代入獲取此時的參數值。

3 AUKF算法

3.1 UKF算法

UKF 算法主要包括系統初始化、狀態預測和測量校正3個部分。

（1）系統初始化

初始化狀態量和誤差協方差矩陣為

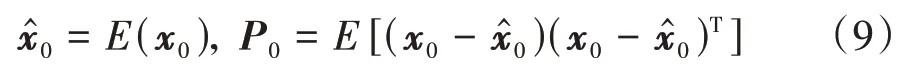
用對稱采樣法生成初始Sigma點，其中為尺度參數：

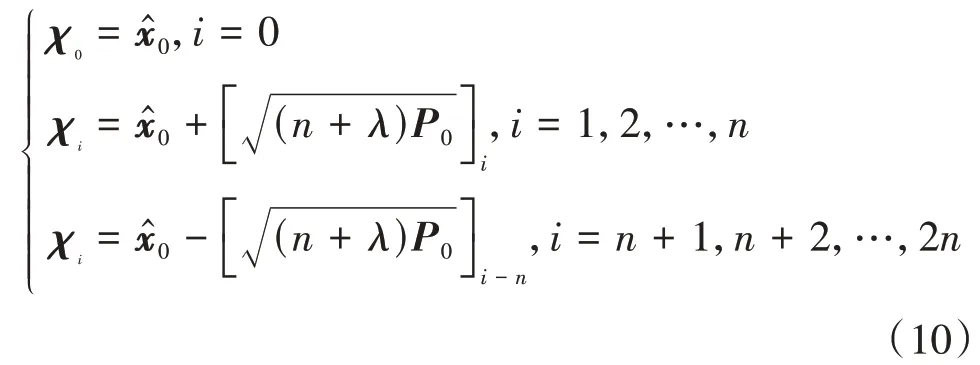
（2）狀態預測

第個采樣時刻，Sigma點構建的矩陣為

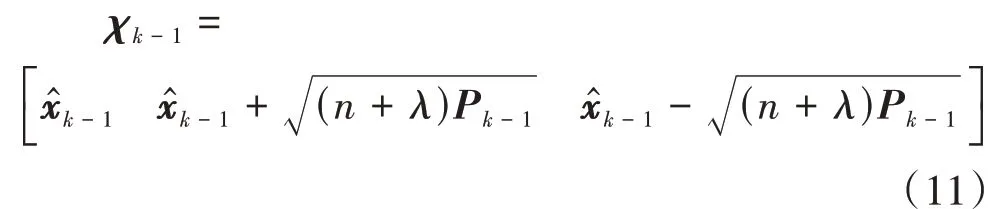
對式（11）的Sigma點進行狀態方程的處理，并對時刻系統狀態量和誤差方差矩陣進行預測：

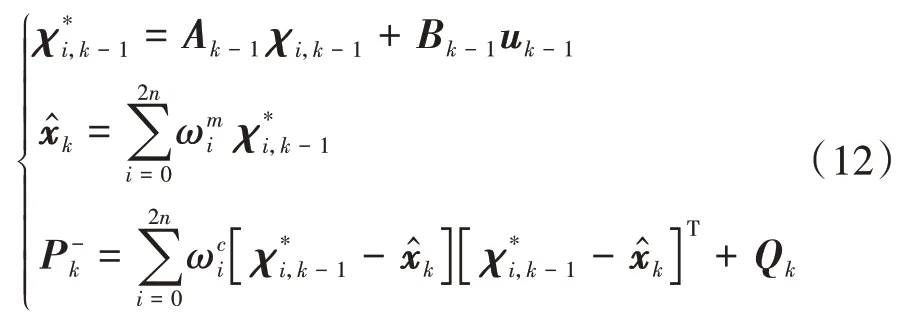
式中Q為時刻的過程噪聲協方差矩陣。

（3）觀測校正

計算時刻的觀測量的估測值：

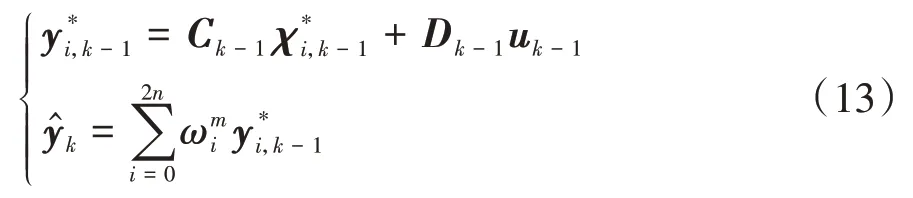
計算時刻觀測量的方差矩陣為

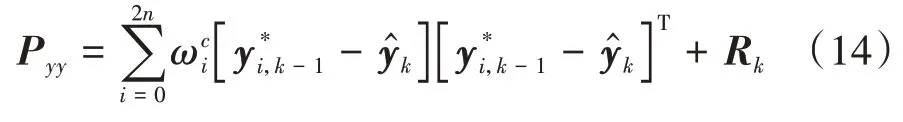
式中R為時刻的測量噪聲協方差矩陣。

計算時刻狀態量與觀測量的協方差為

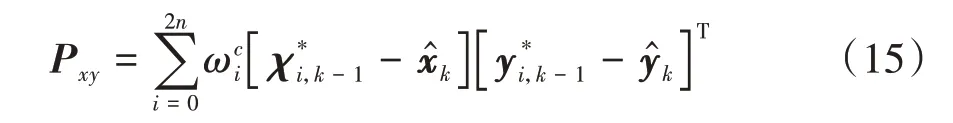
計算卡爾曼濾波增益為

更新狀態量與誤差方差矩陣為

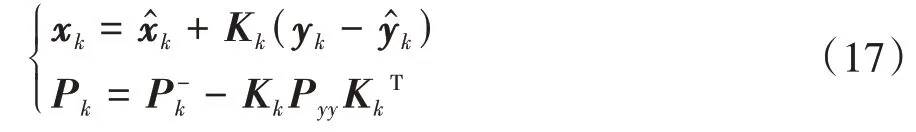
3.2 AUKF算法的實現

UKF算法能夠實現對系統狀態的實時估計。但仍存在以下問題：

（1）由于在非線性系統中存在一些不確定因素，導致過程噪聲協方差矩陣Q和測量噪聲協方差矩陣R難以獲得準確值。而使用經驗法將它們設置為定值則會影響UKF的估計精度。

（2）UKF對RC模型的精度十分依賴，但RC模型的阻容參數辨識存在誤差是不可避免的。當模型誤差較大和R取值不當時，會通過測量校正環節引入較大的狀態估計誤差。

（3）實際應用中常存在SOC 初值存在偏差和測量噪聲異常擾動等突發情形。常規的UKF 對這些情形的自適應能力較有限。

3.2.1 測量噪聲協方差自適應調整

設置越大，表明對測量值的置信度越低，這會導致算法初始的收斂速度慢；設置越小，收斂速度越快，但會導致SOC 估計后期的波動性較大。可見過大或過小的值都會影響SOC 的整體估計效果。因此在濾波算法的初始階段設置較小的值，用表示，使SOC的估計初值快速向真實值方向收斂，等到估計值收斂到真實值附近時，再切換較大的值，用表示，以降低估計值的非線性波動。和的取值與電壓傳感器的測量精度有關，所以在SOC 估計的初始階段，的取值比電壓傳感器精確度低一個數量級，過小容易引起估計值波形在起始階段過沖。則取比傳感器精度高一個數量級的數，過大則會引起值減小，使測量校正失去作用。

根據文獻［21］中提出的濾波器收斂性判據，濾波器發散時，真實的估計誤差要遠大于計算得到的預測誤差。因此，SOC估計的發散條件為

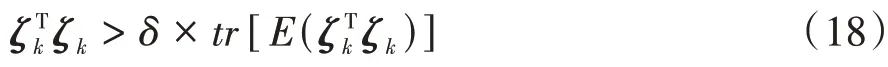
在后續SOC 的估計過程中，能通過影響增益，進而影響SOC 估計的測量校正階段。當傳感器測量誤差較大或RC 模型的誤差較大，即時刻的觀測殘差ζ較大時，如果此時值非0，會在測量校正階段引入較大的估計誤差。因此為該算法設置第2個判據：

若式（20）不滿足，即觀測殘差ζ超過預設閾值時，則將設為無窮大，此時趨于0，相當于只進行狀態預測而不進行觀測校正，只有當測量誤差較低和RC模型精度較高時，才同時進行狀態預測和觀測校正。判據式（20）的引入，有助于降低UKF對RC模型精度和傳感器測量精度的依賴，增強SOC 估計的穩定性。

3.2.2 卡爾曼增益自適應調整

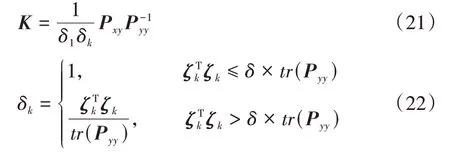
3.2.3 過程噪聲自適應調整

過程噪聲主要反映系統模型的誤差。通過在SOC估計的過程中動態調整，使其能充分反映系統模型本身的誤差，以避免模型誤差造成的SOC 估計精度過多的下降。方法是通過利用多個之前時刻的真實值與估計值的殘差，對下一時刻的Q進行遞推：

式中：-<<；e表示在-1～區間內，由電壓測量值與模型估計值的殘差組成的序列；G表示由e組成的協方差陣；表示該e序列的長度，該值越大，越能充分反映系統的模型誤差，但是計算量也越大。Q由式（24）不斷迭代遞推獲得。

通過在SOC 估計過程中對測量噪聲協方差、卡爾曼增益和過程噪聲協方差進行自適應調整，形成了AUKF算法，如圖4所示。

圖4 AUKF算法流程圖

4 實驗與分析

利用實際測試數據和馬里蘭大學電池數據集，對所提出的AUKF算法的性能進行驗證。

4.1 實驗測試數據

設置恒溫箱溫度為25 ℃，對額定容量為3 A·h、標稱電壓為3.6 V 的18650 三元鋰離子電池充滿電后，采用動態應力測試（dynamic stress test，DST）工況進行放電，放電過程中電池的電壓電流曲線見圖5。

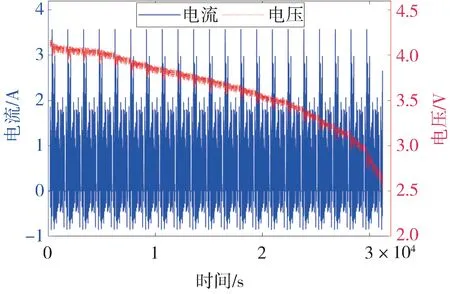
圖5 DST工況下電壓電流測試曲線

圖6展示了采用AUKF 和UKF 算法進行SOC 估計的結果和相對誤差，圖7 為采用AUKF 算法進行SOC 估計過程中的電壓觀測值和模型輸出值、擬合誤差即殘差隨放電時間的變化情況。由圖6 可知，UKF 算法收斂后的相對誤差在3%以內，而AUKF 算法收斂后的相對誤差則更小，接近于零，且具有更快的收斂速度，更高的估計精度，估計值曲線更加平滑和穩定。圖6 和圖7 右圖的綠色虛線表示發散與收斂的界限：在它之前的時刻，由于SOC初始誤差的存在，端電壓的擬合殘差也存在較大偏差，這時式（19）成立，濾波器處于發散狀態，此時選取較小的作為測量噪聲協方差，之后的時刻AUKF 收斂，選取較大的作為測量噪聲協方差。圖7右圖的紅色和藍色虛線分別表示電壓正閾值和負閾值，閾值設為0.03 V。在濾波器收斂后的SOC 估計過程中，由于傳感器測量精度或RC 模型本身的誤差造成一些時刻的觀測殘差大于閾值，則這些時刻的設為無窮大，只進行狀態預測而不進行狀態校正。

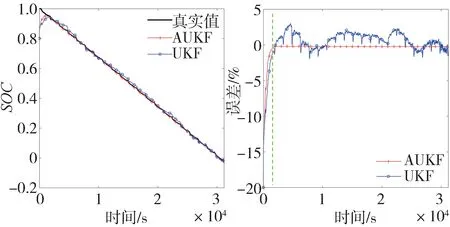
圖6 SOC估計結果與誤差（SOC0=0.8）

圖7 電壓觀測值、模型輸出值和殘差的時間歷程（SOC0=0.8）

為定量刻畫算法的收斂性能，定義“跟隨系數”為SOC 真實值與估計值的誤差絕對值小于0.02 所用的時間與放電總時間的比值。表1 列出跟隨時刻之后的平均絕對誤差（mean absolute error，MAE）和均方根誤差（root mean squared error，RMSE）及跟隨系數。

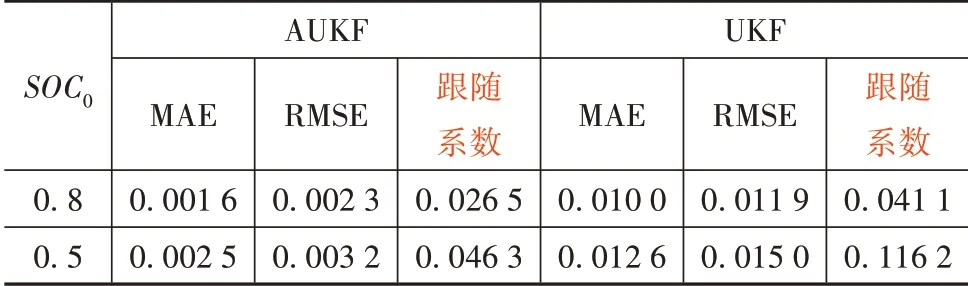
表1 SOC估計誤差和跟隨系數

為進一步驗證不同的SOC估計初值對兩種算法的影響，取=0.5，得到圖8 和圖9。由仿真測試結果可知，取較小的SOC估計初值時，兩種算法下的收斂時間均會變長，跟隨系數都有所增加，圖8 和圖9 的綠色虛線也更加靠右。其中UKF 的跟隨系數增加幅度更大，表明UKF 算法抵抗初值不確定性的穩定性較差。雖然AUKF 算法的估計誤差與初值為0.8 時相比略有增加，但估計誤差MAE 與RMSE 仍保持在較低水平。

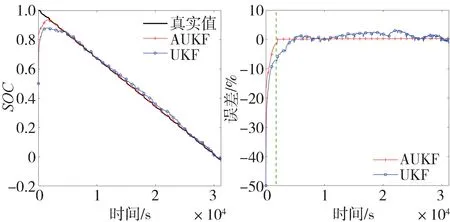
圖8 SOC估計結果與誤差（SOC0=0.5）

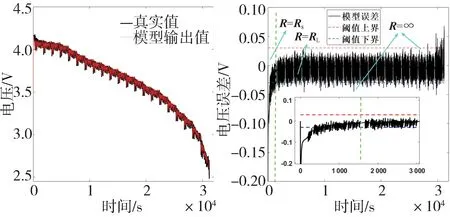
圖9 電壓觀測值、模型輸出值和殘差的時間歷程（SOC0=0.5）

為進一步驗證所提出的AUKF 算法對不同SOC初值的收斂能力，取為0.2、0.4、0.6 和0.8 進行仿真測試，得到結果如圖10 所示。估計誤差和跟隨系數列于表2 中。可知不同SOC 估計初值下，AUKF 均能可靠收斂，跟隨系數都保持在0.07以內。隨著初始誤差增大，跟隨系數升高，總體MAE 和RMSE 誤差增大，但最大值都不超過1%。這表明所提出的AUKF 算法具有較高的估計精度和較好的魯棒性。

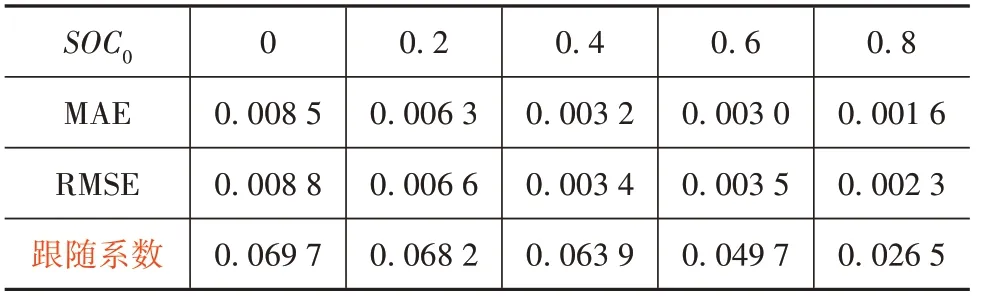
表2 不同SOC估計初值下的計算誤差和跟隨系數

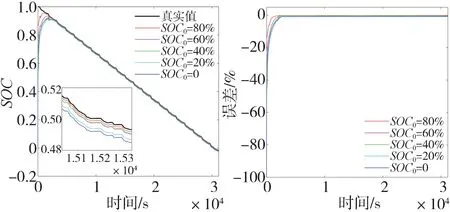
圖10 不同SOC估計初值下的估計效果與誤差

4.2 馬里蘭電池數據集

馬里蘭大學電池數據集使用額定容量為2 A·h、標稱電壓為3.6 V 的18650 三元鋰離子電池進行試驗。該數據集中提供了電動汽車常用的測試工況數據，如US06 工況、聯邦城市行車（federal urban driving schedule，FUDS）工況、北京動態應力測試（Beijing dynamic stress test，BJDST）工況。因此，該數據集很適合驗證本文提出的基于AUKF 的SOC 估計方法。需要注意的是，該數據集中的測試電池是從約80%額定容量時開始放電，在約為20%額定容量時放電結束，該放電區間也是電動汽車實際應用中最常用的放電區間。取=0.6，各動態工況的SOC 估計結果和誤差分別如圖11～圖13 所示，其MAE 和RMSE 計算誤差與跟隨系數列于表3 中。可以看到，在3種不同測試工況下，與UKF相比，AUKF具有更小的跟隨系數和估計誤差，表現出更加優越的性能。

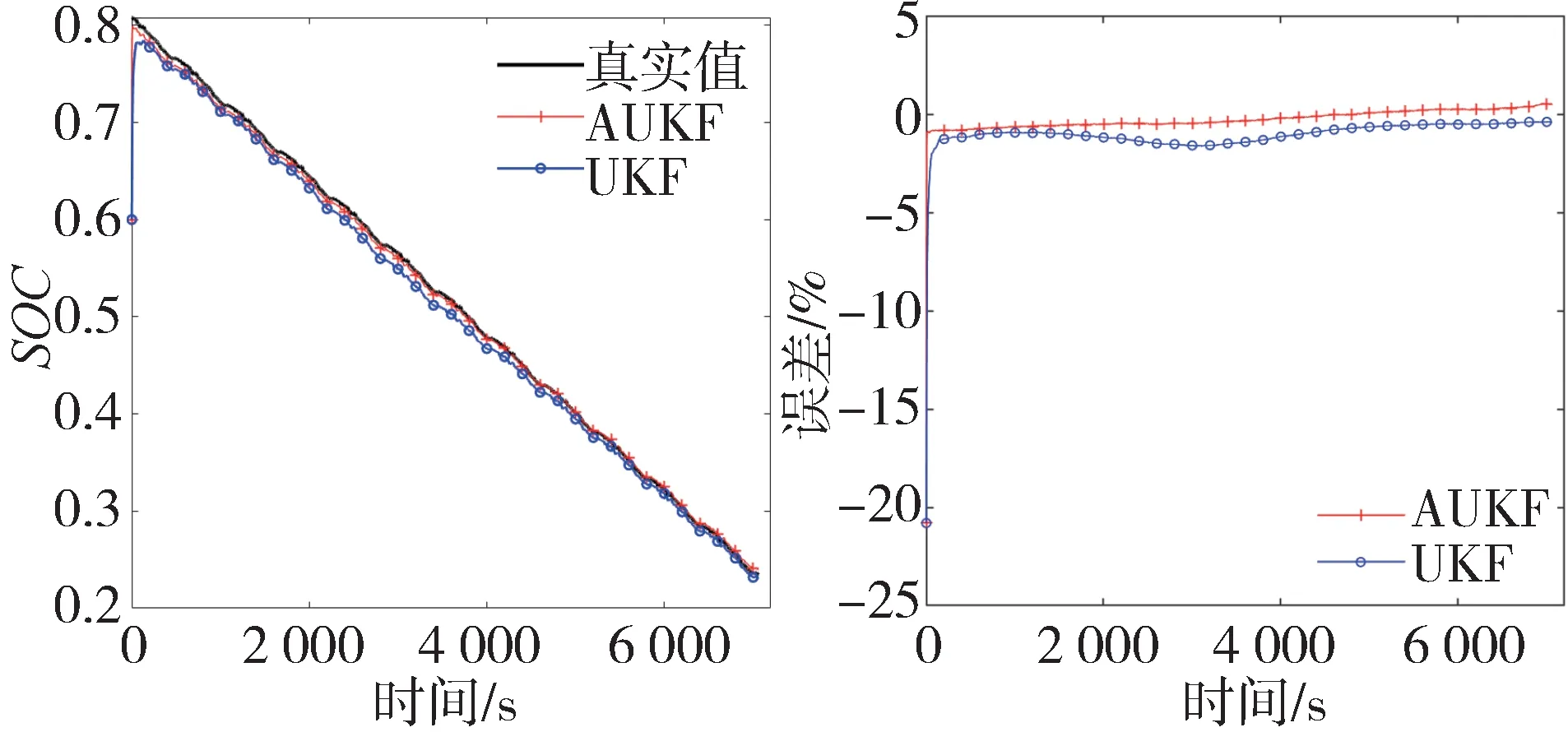
圖11 SOC估計結果和誤差（US06工況）

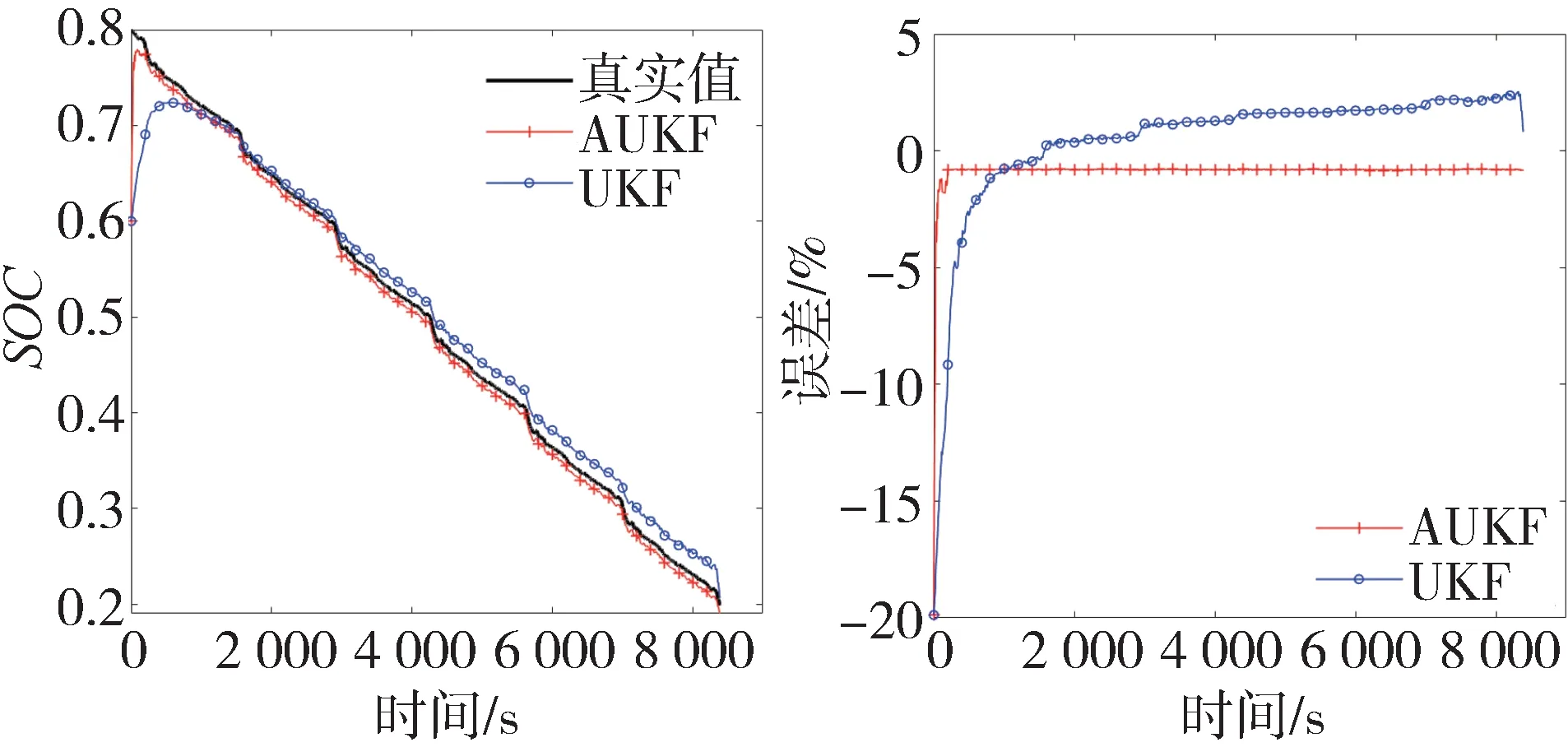
圖12 SOC估計結果和誤差（FUDS工況）

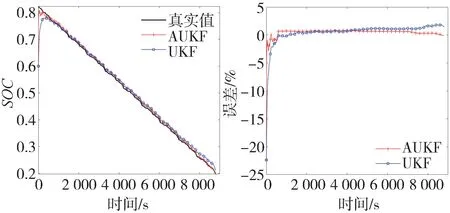
圖13 SOC估計結果和誤差（BJDST工況）

表3 馬里蘭數據集上的SOC估計誤差與跟隨系數

5 結論

首先介紹RC等效電路模型及其數學描述，完成了參數辨識和模型建立工作，并提出了一種阻容參數的二維插值方法，對阻容參數隨SOC 的變化進行建模。其次針對常規UKF 存在的問題，提出了一種AUKF 算法，該方法將濾波器的一般性收斂判據引入UKF 中，并通過對測量噪聲協方差、過程噪聲協方差和卡爾曼增益進行自適應調整，提升了濾波算法的穩定性和收斂性，降低了對電路模型精度的依賴。最后在實際測試數據的DST 工況、馬里蘭大學電池數據集的3 種循環工況中進行實驗驗證。結果表明在不同的測試工況下，與常規UKF 算法相比，所提出的AUKF 算法皆具有較高的估計精度、較小的跟隨系數和較平穩的估計曲線。