實時彩色圖像自適應中值濾波算法的FPGA實現
韓玉鑫,王曉凱,陸金旺
(山西大學 物理電子工程學院,太原 030006)
0 引言
數字圖像在采集、傳輸和處理的過程中,由于設備工作環境的惡劣,會引入一些隨機、離散噪點,降低了圖像質量和視覺效果[1-2]。現實環境中存在多種圖像噪聲,如高斯噪聲、隨機噪聲、瑞利噪聲等[3],圖像降噪應兼顧降噪效果和細節保留這兩方面。
目前對椒鹽噪聲的濾除,有加權中值濾波算法[4]、開關中值濾波算法[5]、自適應中值濾波算法[6]和改進型中值濾波算法[7-10],自適應中值濾波算法運算量大、復雜度高,雖然在PC端可以達到很好的濾波效果,但由于其串行計算的特點,很難滿足對高分辨率、高速圖像實時濾波的要求。FPGA (Field Programmable Gate Array)為半定制電路,可通過流水線等操作實現面積與速度的互換,可直接將算法映射為電路,從而可極大加快算法執行的效率[11-13]。目前彩色圖像的中值濾波主要是將RGB彩色空間轉換到YCbCr彩色空間,然后對Y分量進行濾波。由于YCbCr色彩空間會損失掉色度信息,因此降噪后的圖像會產生失真。
鑒于此,結合HSI(Hue Saturation Intensity)色彩空間特點設計了一個基于FPGA的實時彩色圖像自適應中值濾波系統,極大的增強了濾波的實時性。最終實驗結果表明該系統可對2 k(2 560×1 440) @60 Hz彩色視頻實時處理,且濾波后圖像色彩還原度高,具有廣闊的應用前景。
1 RGB-HSI模塊
本節將介紹HSI彩色模型,并將幾何推導算法和分段定義算法在FPGA硬件上實現。
1.1 HSI彩色模型
我們觀察物體時,用其色調、飽和度和亮度來描述這個物體。HSI彩色模型可從攜帶彩色信息(色調和飽和度)的圖像中去除強度分量的影響。因此,HSI模型是開發基于彩色描述圖像算法的理想工具。如圖1所示圖(a)為基于圓形彩色平面的HSI彩色模型,圖(b)為基于三角形彩色平面的HSI彩色模型。以圖(a)為例,白色頂點與黑色頂點相連的軸為亮度軸,飽和度為像素點與亮度軸的距離,色調為像素點與紅色軸的夾角,在亮度軸上飽和度為0且無色調。常見的RGB-HSI轉換算法共有5種,算法的具體推導和公式可查閱文獻[14]獲得。由于HSI各分量間相對獨立,故可以根據具體應用,將不同算法的HSI公式交叉使用。下節分別在FPGA上實現幾何推導算法和分段定義算法,通過對兩種方法轉化后圖像的質量進行對比,在轉化精度與消耗硬件資源之間進行權衡,選擇合適的算法。
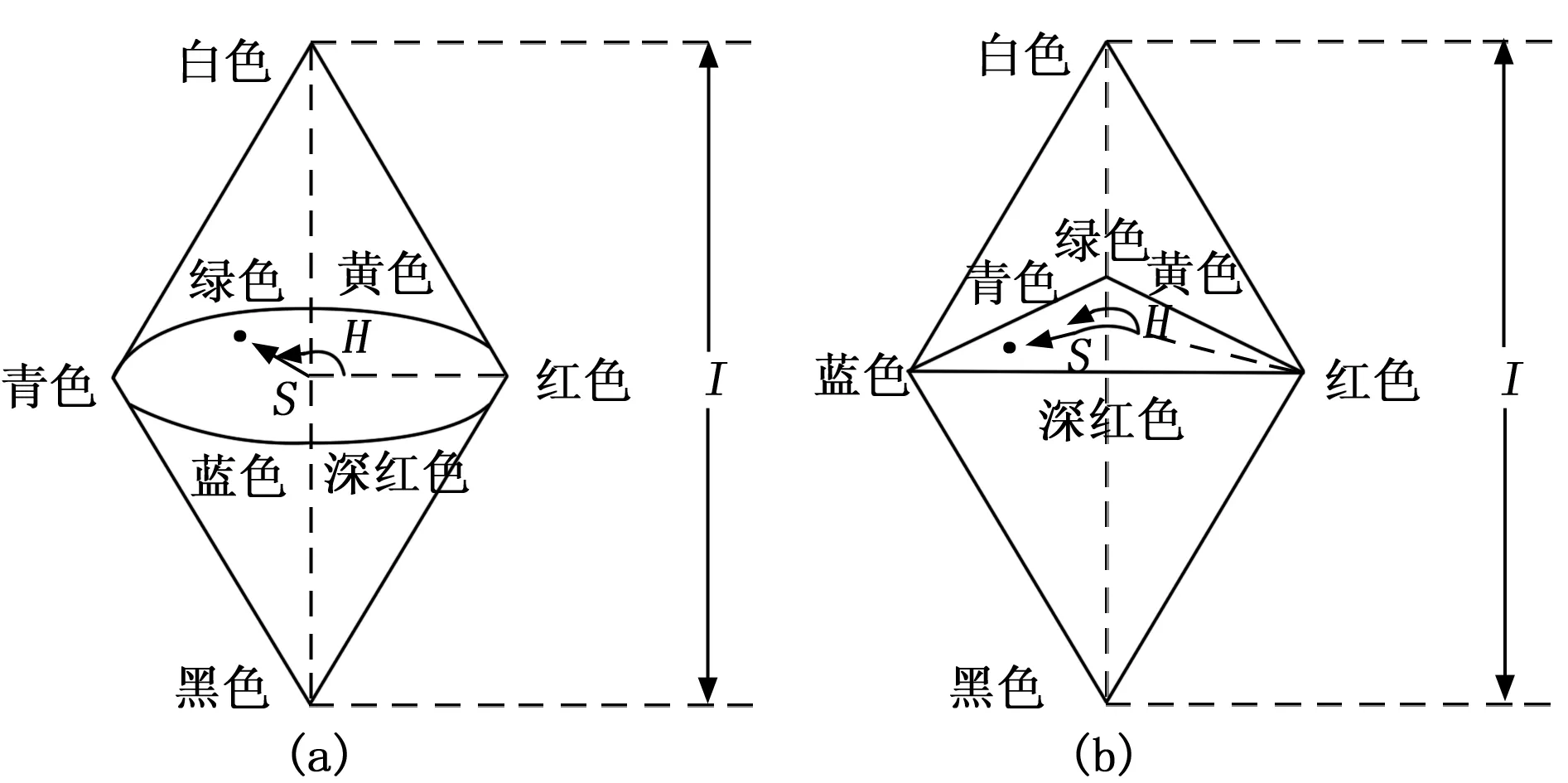
圖1 HSI彩色模型
1.2 幾何推導法硬件實現
由于FPGA只能進行整數計算,所以將浮點數轉換為整數進行計算,由8位2進制數表示[0,1],量化精度為0.003 921。給定一幅RGB彩色圖像,每個RGB像素的H分量可由下式得到:
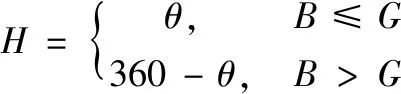
(1)
式中,
(2)
飽和度分量由下式給出:
(3)
最后強度分量由下式給出:
(4)
在硬件中計算arccos(x)比較困難,主要有以下幾種計算方式:
1)通過Xilinx官方提供的CORDIC IP核,該IP核可計算arctan(x),利用arctan(x)與arccos(x)轉換關系即可完成對arccos(x)的計算。由于在原公式的基礎上加入了開方和除法等復雜運算,而IP核直接計算arctan(x)需要20個時鐘周期的延遲,所以增大了硬件資源的消耗和處理時延;
2)通過下式:
arccos(x)=
(5)
上式為arccos(x)的泰勒展開式,可通過上式選取合適的n逼近arccos(x),但是當|x|接近1時,上式收斂速度很慢,所需硬件乘法器、除法器和加法器急劇增加,處理時延也會進一步加大,無法滿足圖像地實時處理;
3)使用ROM查找表的方式實現,將提前計算好的數值從ROM中讀取出來,只需要2個時鐘周期就可以完成運算,可滿足實時圖像處理。
為符合處理實時圖像的要求,選取ROM查找表方式。當x趨近于1時,由于arccos(x)的導數趨于無窮大,所以arccos(x)會產生較大誤差。將x分別量化到[0,255]和[0,4 095],通過這兩種量化精度之間的對比,說明上述誤差對H分量的影響。
乘法器實現主要分兩種情況:在乘一個定值時,為節約硬件資源,采用FPGA擅長的移位運算;在乘一個變量時,為保證系統性能,采用Multiplier IP核實現。除法器實現也分為兩種情況,當除數是一個定值時,采用下式實現:
(6)
其中:2n為大于除數的最小整數,m控制計算的精度,m越大精度越高。例如,計算x/3,我們取2n為4,m為8,公式就變為x×341÷1024,乘法采用上述左移方式實現,由于除數為2的整數次冪,除法采用右移相應的位數即可實現。當除數是變量時,采用Divider IP核計算,計算結果將余數舍去,只取商即可。開平方的運算通過調用CORDIC IP核實現。
通過硬件轉換與軟件仿真結果對比發現,S分量和I分量的誤差均在±1以內,而H分量在某些像素點的誤差達到20。這是由于硬件計算開平方、除法和反余弦均有誤差,而開平方的誤差會引入到除法計算中,加大除法計算的誤差,除法計算的誤差又會被引入到反余弦中,這樣會將誤差逐級放大。在1.4節會通過具體圖片的硬件仿真說明這種誤差對色彩空間轉換的影響。
1.3 分段定義法與幾何推導法相結合
由于HSI各分量相互獨立,所以可將分段定義算法與幾何推導算法相結合,即H分量通過分段定義法求得,S分量、I分量通過幾何推導算法求得,其中上節已完成幾何推導法S、I分量的計算,這節主要完成對分段定義算法中H分量的計算,H分量由下式給出:
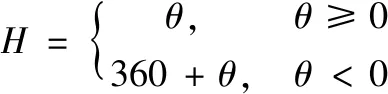
(7)
式中,θ由下式給出:
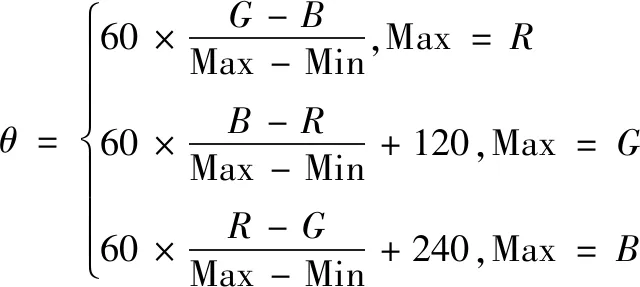
(8)
其中:Max=max(R,G,B),Min=min(R,G,B),由于分子的減法會存在負數的情況,所以使用補碼進行減法運算。為節約硬件資源,將Divider IP核配置為無符號除法器,這就需要求一個補碼的絕對值。當補碼的符號位為0時,絕對值為其自身。當補碼符號位為1時,可通過2n-complement進行計算,其中n為補碼的位寬。下一小節將通過具體圖像進行硬件仿真,分別通過MSE(mean squared error)、PSNR (peak signal to noise rate)、SSIM(structural similarity)等評價指標對3種方式生成的HSI進行對比分析。
1.4 硬件仿真對比結果
本節將通過由軟件轉換后的HSI和FPGA硬件轉換后的HSI進行對比,分析上述各種轉換方法的差異。如圖2所示,其中圖a、b、c分別為MATLAB使用幾何推導算法轉化后的H、S、I分量圖,圖d、e、f、g、h為通過Modeisim硬件仿真生成的HSI分量圖。其中圖d、g為幾何推導算法H分量的轉換結果,它們區別為圖d中arccos(x)的x量化精度為0.003 92,而圖g中arccos(x)的x量化精度為0.000 244 2。圖e、f分別為幾何推導算法S、I分量的轉換結果,圖h為分段定義算法H分量轉換結果。

圖2 HSI對比圖
為了分析硬件轉換的精度,分別計算軟件與硬件轉換結果之間的MSE、PSNR、SSIM[15-16],如表1所示,其中H1為幾何推導算法(arccos(x)中x的量化精度為0.003 92) 的色度,H2為幾何推導算法(arccos(x)中x的量化精度為0.000 244 2) 的色度,H3為分段定義算法轉換的色度,S、I為幾何推導法轉換的飽和度和亮度。對比3個H分量,分段定義算法轉換較為精確,結構相似性可達到99.9%。而幾何推導算法即使是將arccos(x)的x量化精度提升至0.000 244 2,相應的結構相似性僅僅從99.68%提升至99.72%,未達到分段定義算法的精度,不僅如此,幾何推導法在計算H分量時,進行了復雜函數(開平方和反三角函數)的計算,這些會消耗大量的硬件邏輯資源,而分段定義法最復雜的計算為除法運算,所需硬件邏輯資源較少。分段定義算法H分量結構相似性達到99.9%,幾何推導算法S、I分量結構相似性均達到了99.9%,因此本文采用分段定義法計算H分量,幾何推導法計算S分量和I分量。

表1 各評價標準對比
2 濾波窗口和排序模塊
本節將介紹3×3、5×5和7×7濾波窗口的獲取,以及窗口內最小值、最大值和中值的獲取,并將其在硬件上實現。
2.1 自適應濾波窗口的生成
本系統自適應中值濾波支持最大濾波窗口為7×7,為實現實時圖像處理,此模塊直接生成7×7的濾波窗口,3×3、5×5濾波窗口可直接從7×7的濾波窗口得到。為保護圖像細節,我們采用擴展鄰近像素點的方式對邊界進行填充。
我們采用RAM存儲圖像前6行的數據,而輸入的數據作為第7行,這樣可以節省一行RAM硬件資源。由于圖像分辨率為400×480,HSI分量需要25 bit來存儲,其中H為9 bit、S為8 bit、I為8 bit,因此我們需要調用6個位寬為25 bit、存儲深度為400的Simple Dual Port RAM。RAM存儲時序如圖3所示,由于RAM讀取數據需要一個時鐘周期,所以要將輸入像素數據延時一個時鐘周期,延時后的像素數據與6個RAM讀出的數據構成一個“七行一列”的像素數據。為防止RAM讀寫沖突,輸入的像素數據在RAM1讀出數據后寫入RAM1中,相應的RAM1讀出的數據在RAM2讀出數據后寫入RAM2中,以此類推。連續緩存7個“七行一列”的像素數據就可以生成7×7的濾波窗口。因為需要等3行像素數據的緩存,所以第一個7×7的濾波窗口與第一個像素相差1 200個有效像素時鐘。
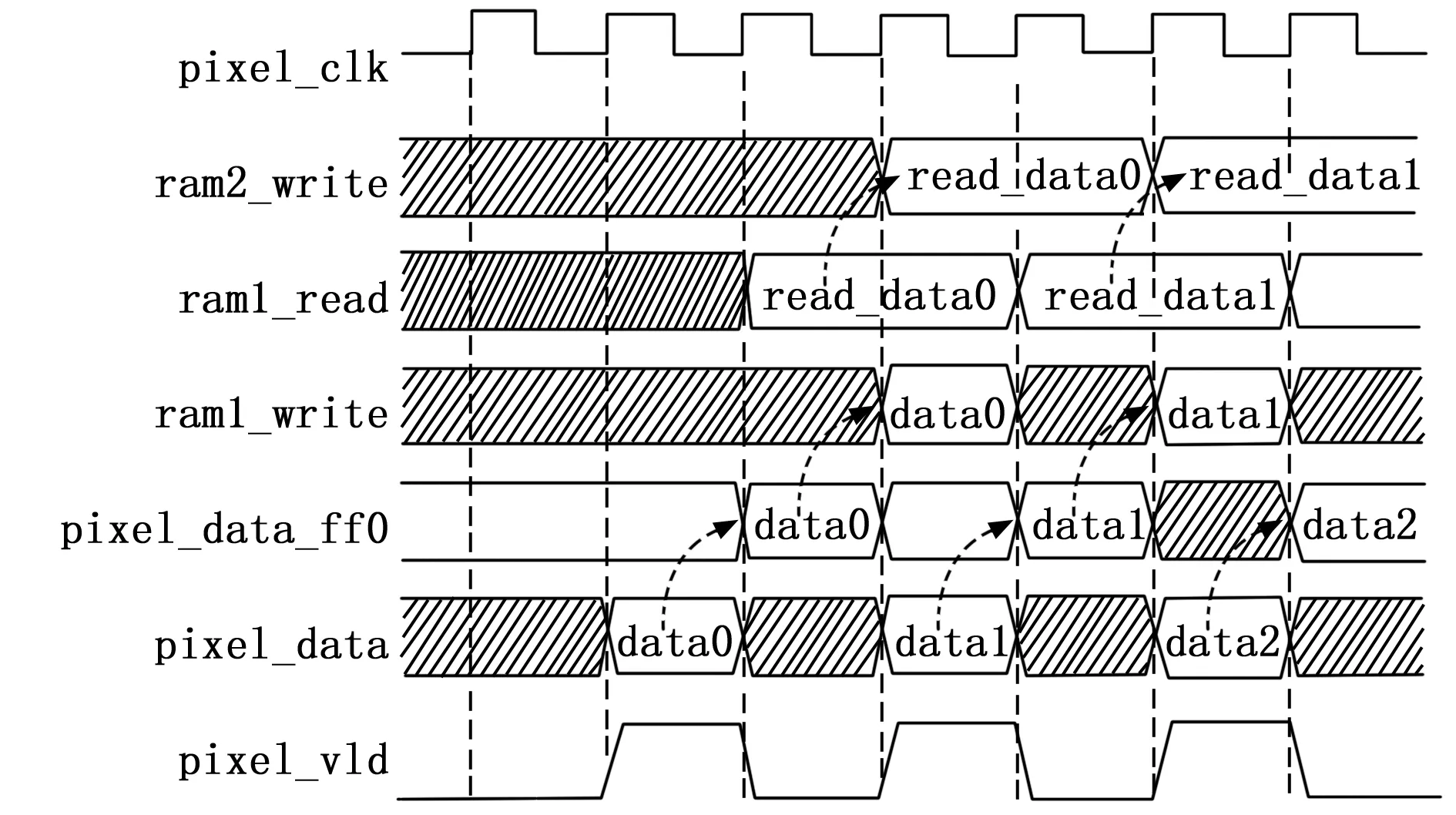
圖3 RAM存儲時序
2.2 排序模塊
FPGA是以并行計算為主,通過硬件描述語言實現電路的映射,與單片機順序操作有很大區別。FPGA實現算法通過觸發器和邏輯門電路組合形成電路,更加接近硬件底層的實現,其可在一個時鐘周期內完成多個任務,達到并行加速的目的[17]。由于要達到處理實時圖像的目的,比較矩陣排序器[18]可以滿足實時的要求,該排序器原理為將每一個元素與序列中所有的元素進行比較,大于被比較元素則得分為1,否則得分為0,當所有元素比較完之后,將所得分數進行累加,獲得該元素在序列中最終索引值[18]。具體實現步驟為,將序列中的所有元素分別作為一個矩陣的行值和列值,除去對角線上的元素,將每列值分別與每個行值進行比較,并記錄每對行列值的比較情況,比較完成后,對矩陣每一行的所得分進行相加,即可得到該行對應元素的最終索引值,但是隨著輸入元素的增加, FPGA硬件邏輯資源的消耗呈指數增加[18]。由于本文最大輸入元素為49,故本文將Priyadarshan Kolte和Roger Smith等人提出的快速中值濾波算法[19]與上述算法相結合,采用流水線方式設計,最大時延為9個時鐘周期。下面舉例說明該算法排序過程。
假設有一待排序數組{10,10,50,40,30},設D0=10、D1=10、D2=50、D3=40、D4=30,考慮到數組中有相同元素,而且還要進行累加運算。相同元素排序按照原數據誰在前誰優先的原則,即在每個數據與其它數據比較時,根據數據在原數組中的位置,比較器的類型要發生變化[20]。例如Dm與Dn比較時,如果m>n,則選用“≥”比較器,如果m

表2 數據比較結果表
對于7×7濾波窗口計算過程如圖4所示(箭頭所指的方向為升序方向)。
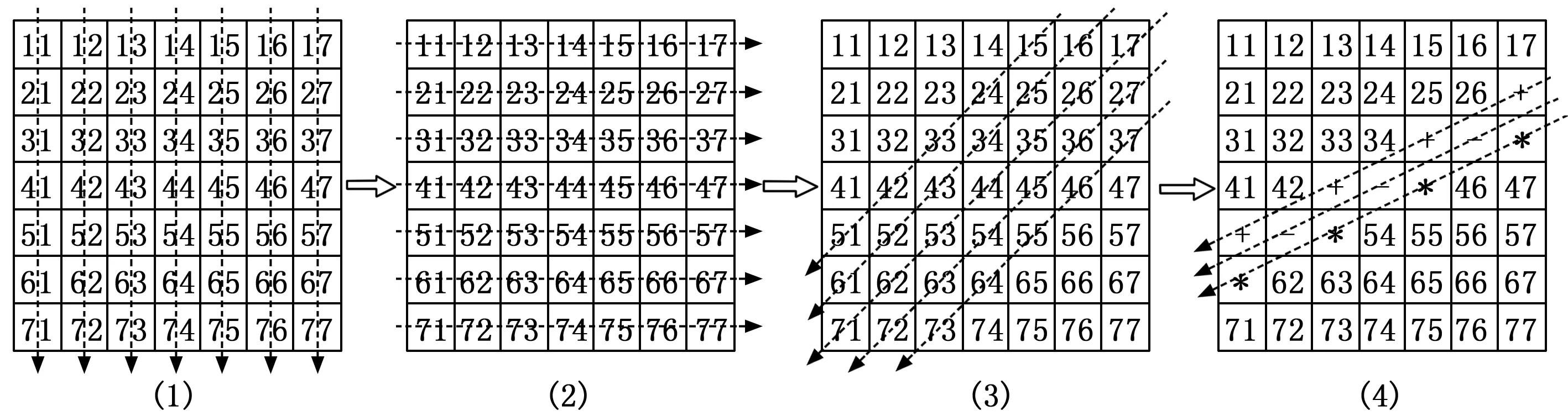
圖4 7×7窗口中值獲取流程
(1)將7×7濾波窗口中每列像素按照箭頭方向做升序排列;
(2)在(1)的基礎上將每行像素按照箭頭方向做升序排列,則像素點11為最小值像素,像素點77為最大值像素;
(3)在(2)的基礎上把45度對角線方向上的5列像素按箭頭方向做升序排列;
(4)在(3)的基礎上,將像素點27、35、43、51(“+”所在位置的像素點),像素點36、44、52(“-”所在位置的像素點),像素點37、45、53、61(“*”所在位置的像素點),按照箭頭方向做升序排列,形成新的7×7濾波窗口;
(5)在(4)處理后的7×7濾波窗口中,取像素點37、44、51的中值,即為7×7濾波窗口內的中值。
其中sort5、sort6、sort7采用上述的比較矩陣排序法(sortx表示對x個元素進行排序),排序需要2個時鐘周期。sort3直接采用邏輯門實現,處理需要1個時鐘周期。sort4則通過調用sort3,然后將第4個元素插入到合適位置,處理需要2個時鐘周期。由于3×3、5×5窗口排序與7×7窗口類似,此處不再贅述。
3 自適應中值濾波
自適應中值濾波算法是根據不同噪聲濃度來自適應地調節濾波窗口[21],通過濾波窗口內的極值點來判別噪聲與信號。此算法實現需要兩個進程,將其中變量表示為:Mmax表示Mxy允許的最大濾波窗口,Imin表示Mxy中的最小亮度值,Imax表示Mxy中的最大亮度值,Imed表示Mxy中亮度值的中值,Ixy表示坐標(x,y)處的亮度值。
自適應中值濾波兩個進程如下:
(1) 進程A,A1=Imed-Imin,A2=Imed-Imax,如果A1>0且A2<0,則轉到進程B判斷原像素點是否為噪聲點,否則增大窗口尺寸,如果當前窗口尺寸≤Mmax,則重復進程A,否則輸出Imed。
(2) 進程B,B1=Ixy-Imin,B2=Ixy-Imax,如果B1>0且B2<0,則輸出Ixy,否則輸出Imed。
傳統自適應中值濾波算法由于只將局部極值點作為噪聲的判定依據,所以此過程很容易造成噪聲的誤判。由于椒鹽噪聲集中在HSI彩色模型的亮度軸上,其飽和度是接近于0的,故本文在傳統自適應中值濾波算法的基礎上,加入S分量進行噪聲的判別,可以減少圖像細節的丟失。進程A不變,進程B調整為:如果B1=0或B2=0并且S接近0,則輸出Imed,否則輸出Ixy。
4 HSI-RGB模塊
本模塊的輸入為濾波后HSI分量,目的是實現彩色圖像的還原。本節包括了HSI-RGB的轉換公式,以及在硬件上的具體實現,同時結合RGB-HSI模塊,將一幅圖片通過RGB-HSI和HSI-RGB之后,與原圖像進行對比,分析其還原精度以及硬件邏輯資源消耗情況。
4.1 HSI-RGB轉換公式
公式的選取取決于H的值,在原色分割中有3個相隔120。的扇區(見圖1)。當H的值在RG扇區時,即0≤H<120,RGB分量由以下公式[22]給出:
(9)
(10)
G=3I-(R+B)
(11)
H值在GB扇區時,即120≤H<240,RGB分量由以下公式[22]給出:
H=H-120
(12)
(13)
(14)
B=3I-(R+G)
(15)
H值在BR扇區時,即240≤H<360,RGB分量由以下公式[22]給出:
H=H-240
(16)
(17)
(18)
R=3I-(B+G)
(19)
上述的公式具體實現將在下節詳細討論。
4.2 硬件實現
為減少硬件邏輯資源的消耗,可添加扇區標志位,只需實現如下公式即可:
(20)
(21)
c=3I-(a+b)
(22)
通過扇區標志位,根據不同扇區公式將結果分別賦值給RGB即可。對于三角函數的計算,我們采用1.2節中ROM查找表的方式實現。與之不同的是,由于分子分母同時存在余弦函數,可以使用串行方式分別計算兩個余弦函數,但是這樣會使輸出多延時兩個時鐘周期,所以我們采用同時計算的方式。通過使用Dual Port ROM,這樣不僅可以同時完成兩個余弦函數的計算,而且所用的ROM資源與計算單個余弦函數相同,可節省一半的ROM資源。可以利用余弦函數的性質,僅僅需要計算[0,90]即可,將計算結果量化到[0,255],這樣只需要一個存儲寬度為8 bit、 存儲深度為91的ROM即可。下節將1.4節中生成的HSI分量通過本模塊進行圖像的還原,并與原圖像進行比較,分析其還原準確度。
4.3 還原精度分析
本節將1.4節中生成的HSI圖像通過硬件進行還原,將生成圖像與原圖進行對比,進一步說明分段定義算法和幾何推導算法相結合的轉換精度。如圖5所示,其中圖a為原始圖像,圖b(arccos(x)中x的量化精度為0.003 92)和圖c(arccos(x)中x的量化精度為0.000 244 2)為經過幾何推導算法轉換后復原的圖像,圖d為經過幾何推導算法和分段定義算法相結合轉換后復原的圖像,從視覺上難以分辨差別。我們將從MSE、PSNR、SSIM分析復原圖像與原始圖像之間的差別。
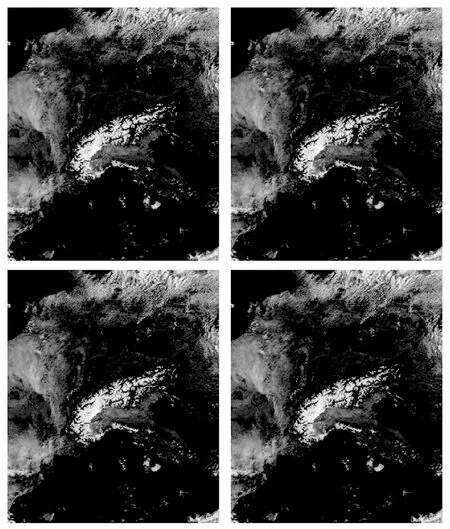
圖5 原圖與復原的圖像
如表3所示,c圖的還原精度較b圖而言有所提升,但是這種提升是以犧牲較多邏輯資源為代價得到的,結構相似度提高了大約0.7%。相比之下,d圖的結構相似度為99.859%,比b圖提升了2.872%,比c圖提升了2.254%。d圖的峰值信噪比為46.87,比b圖高9.6,比c圖高8.38。不僅如此,幾何推導算法和分段定義算法相結合所用硬件邏輯資源比幾何推導算法少的多,具體如表3所示,其中LUT減少了37.2%,LUTRAM減少了82%,FF減少了59%,DSP減少了100%。進一步說明了該方法不僅轉換精度高,而且硬件邏輯資源消耗較少,適合在FPGA硬件中實現。
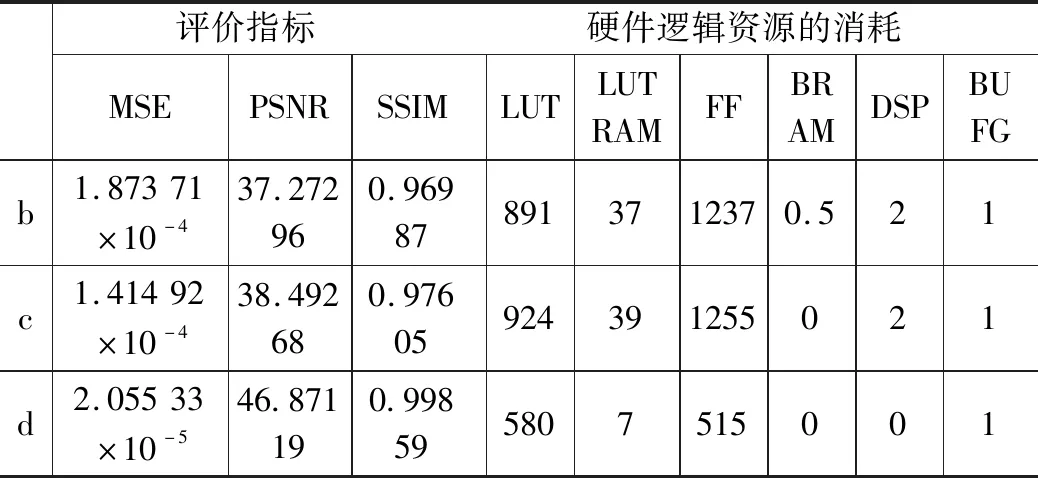
表3 復原圖像質量以及所用硬件資源
5 系統性能分析
系統結構框圖如圖6所示,RGB格式數據先經過RGB2HSI模塊,將RGB格式轉化為HSI格式,處理所需14個時鐘周期,其次通過濾波窗口生成模塊,處理所需1 200個(以400×480分辨率為例,延時3行像素數據400×3=1 200)時鐘周期,接著經過比較排序模塊,處理所需9個時鐘周期,然后通過自適應中值濾波模塊,處理所需1個時鐘周期,最后將處理后的HSI數據通過HSI2RGB模塊將HSI格式轉化為RGB格式,完成對原彩色圖像的還原,處理所需27個時鐘周期。由于多個模塊采用面積換取速度的思想,使用流水線方式實現各模塊,故系統處理時間達到了1 251個時鐘周期,但這也使得系統支持時鐘頻率更高。以Xilinx公司的xc7a100tfgg484-2芯片為例,當系統時鐘為222 MHz時,Worst Negative Slack(WNS)為0.025 ns,Worst Hold Slack(WHS)為0.043 ns,Worst Pulse Width Slack(WPWS)為1.446 ns,所有的端點都滿足時序要求,該系統可以穩定運行。系統最高可對2 k(2 560×1 440)@60 Hz視頻進行實時處理,所需像素時鐘為2 560(1 440×60=221 MHz,滿足系統要求,此時系統時延為14+2 560×3+9+1+27=7 731個時鐘周期(1×10-6/222 s),處理時延為347 90 ns。
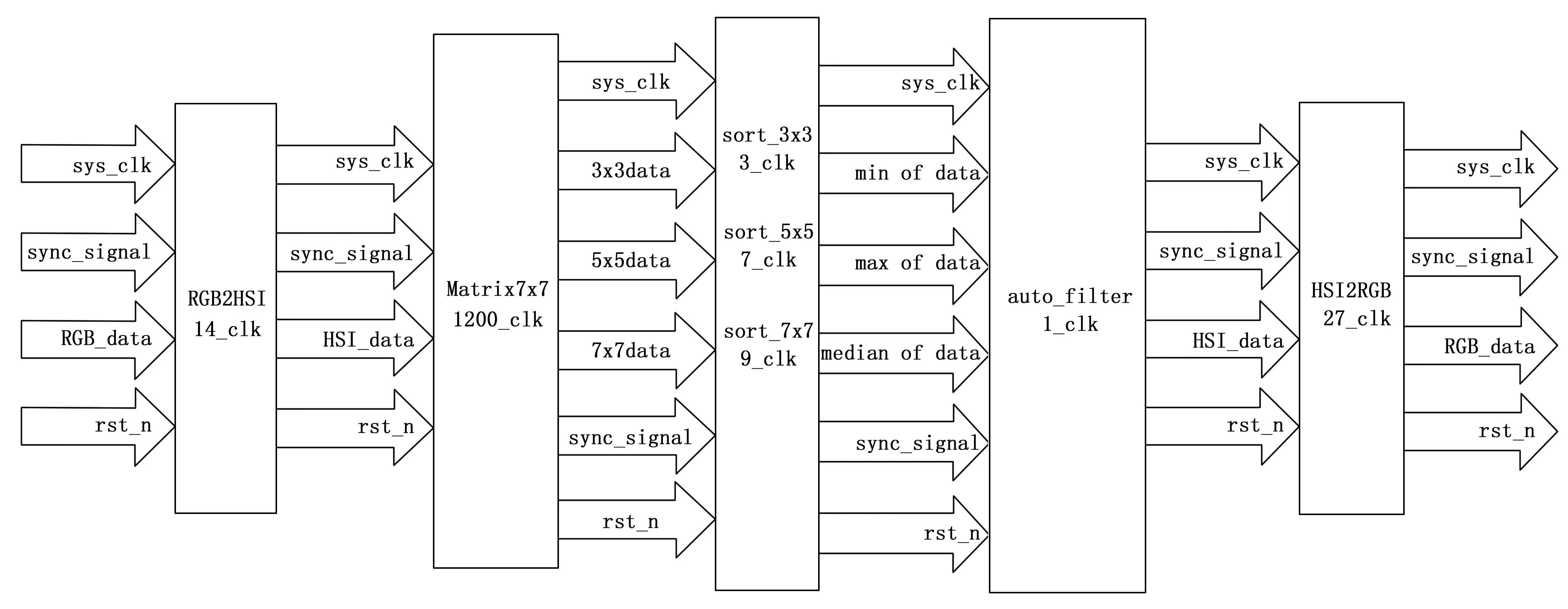
圖6 系統結構框圖
通過MATLAB將原圖像分別添加不同概率的椒鹽噪聲,分別將不同概率噪聲的圖像通過硬件仿真,觀察其降噪效果。硬件仿真通過Modelsim進行仿真,在激勵文件中,按照bmp文件格式將圖片數據讀入,并且按照RGB時序輸入到系統中,將處理后的圖像數據以bmp文件的格式寫入。如圖7所示,第一行為添加不同概率椒鹽噪聲的原圖像,第二行圖為YCbCr彩色空間自適應中值濾波后的圖像,第三行為HSI彩色空間自適應中值濾波后的圖像。椒鹽噪聲的概率分別為20%、30%、40%、50%、60%、70%。從中可得出,HSI彩色空間自適應濾波后的圖像色彩較為鮮艷,色彩還原度好。當噪聲概率小于60%時,降噪后的圖像細節保留完整,且無明顯的噪聲點,當噪聲達到70%時,降噪后的圖像出現明顯的噪聲點。

圖7 降噪前后圖像對比
為了對比不同噪聲密度降噪效果,分別計算兩種色彩空間濾波后圖像與原圖像之間的MSE、PSNR、SSIM。如圖8所示,當椒鹽噪聲概率達到70%時,降噪效果明顯下降,HSI色彩空間降噪后圖像與原圖的結構相似度為76.7%。在噪聲概率小于60%時,HSI色彩空間降噪后圖像與原圖的結構相似度均可達到90%以上,而YCbCr色彩空間降噪后圖像與原圖的結構相似度僅達到80%以上。當噪聲概率為10%時,HSI色彩空間降噪后圖像與原圖的結構相似度可達到99%,而YCbCr僅為86%。當噪聲概率小于90%時,HSI彩色空間的各項指標(MSE、PSNR、SSIM)均優于YCbCr彩色空間。HSI彩色空間降噪后圖像細節保留完好,未出現圖像模糊,達到了在濾除噪聲的同時減少細節損失的目的。如表4,為2種不同的彩色空間(YCbCr和HSI)采用相同自適應濾波所消耗的硬件資源,由于HSI為非線性轉換,而YCbCr為線性轉換,故HSI所消耗硬件資源會更多。但是HSI彩色空間濾波效果提升較大,很好地保留了圖像細節,對后續的圖像處理影響較小。

圖8 濾波后圖像MSE、PSNR、SSIM

表4 消耗硬件資源對比
6 結束語
實時彩色圖像自適應中值濾波的FPGA實現具有重大的實踐意義和研究價值。本文在深入研究HSI彩色空間的基礎上,結合兩種不同的RGB-HSI轉換算法,在硬件上達到RGB-HSI高精度的轉換與還原。結合并行排序算法和快速中值濾波算法,在減少硬件資源消耗的同時,完成對7×7窗口內元素的快速排序。該系統在硬件資源、精度和速度等方面滿足FPGA的設計理念,可廣泛應用于光學條紋圖像的相位分析、智能監控等領域。

