基于改進動態系統穩定估計器的機器人技能學習方法

金聰聰 劉安東 LIU Steven 張文安

近年來,機器人產業高速發展,整體規模持續增長,在制造業和服務業等眾多領域都有廣泛應用.隨著工業產品迭代速度日益增長,個性化需要與日俱增,傳統依靠手工編程完成特定任務的方法難以適應新的需求.因此,迫切需要開發簡單實用,且可以靈活適用于多種任務的機器人技能學習方法.

機器人示教學習(Learning from demonstration,LfD)的靈感最初來源于人類的模仿學習,近幾年獲得學術界和工業界的廣泛關注[1–4].機器人通過觀察用戶演示來學習新技能,同時將新技能泛化到不同場景下的相似任務中去,一般包含演示、學習、復現三個階段.演示階段需要解決的問題是如何向機器人進行技能演示,常用的方法有視覺示教、動覺示教、遙操作示教和雙臂示教.學習階段是對技能進行建模,抽象的技能符號由示教數據具體表示,然后利用示教數據訓練模型參數.復現階段的性能主要體現在穩定性、復現精度、泛化能力和抗干擾性能4 個方面.

動態系統(Dynamical system,DS)是對機器人技能進行建模的常用方法[5],該方法將規劃和執行集成到一起,并將所有可能的解決方案嵌入到模型中以實現目標[6].在非線性DS 基礎上發展起來的動態運動原語只要進行一次演示就可以對運動進行建模[7],動態運動原語描述的運動模型由非線性DS和線性DS 組成,其中非線性部分保證了軌跡復現的相似度,線性部分則確保了模型全局穩定性,兩者的切換依靠相位變量平穩進行.盡管動態運動原語提供了一種有效而精確的方法來對復雜的動態進行編碼,但是單變量編碼丟失了各自由度之間的相關信息,而且該方法本質上仍依賴于時間,在面對時間擾動時需要用啟發式方法重置相位變量[8].

為彌補動態運動原語的缺陷,文獻[9]提出了動態系統的穩定估計器(Stable estimator of dynamical systems,SEDS).它首先利用高斯混合模型(Gaussian mixture models,GMM)和高斯混合回歸(Gaussian mixture regression,GMR)的概率學習方法對軌跡進行初步擬合.概率學習方法是軌跡編碼中的常用方法,它可以保留演示的固有可變性[10],但是無法確保訓練得到的動態系統具有全局穩定性.因此SEDS 在后續優化中加入了穩定性約束,確保機器人在不受擾動的情況下能夠到達目標點.然而,過于嚴格的穩定性約束可能會在學習過程中限制模型的精度.針對SEDS 方法中穩定性和精度難以平衡的問題,文獻[11]利用微分同胚變換改進了SEDS,稱作τ-SEDS.該方法在保證系統穩定性的同時,很大程度上克服了模型的精度問題.但是增加了模型復雜度,導致學習更加耗時,僅限于離線學習.DS 方法的快速穩定學習[12]同時考慮了估計DS 的穩定性、準確性和學習速度三個因素.DS方法快速穩定學習的快速學習能力在很大程度上方便了它的實際應用,但在穩定性和準確性方面還不夠優越.文獻[13]提出了一種基于流形浸沒和淹沒的學習方法來解決精度與穩定性的矛盾,該方法保證了有效提取動力學特征和穩定形式的高精度,而且能處理交叉運動的情形,但模型復雜度較高.

SEDS 中另一個值得注意的問題是混合高斯分量個數的選取,但是對于該問題的相關研究較少.過多或者過少的分量個數選取都會導致模型無法有效提取演示的動力學特征,因此該問題具有一定的研究價值.通常用于確定有限混合模型的最佳分量的方法是貝葉斯信息準則[14],然而這種模型選擇方法存在一些明顯的缺陷[15],常常過高估計模型分量的個數,導致過擬合.貝葉斯非參數模型是一種定義在無限維參數空間上的貝葉斯模型,其利用在適當數量的模型分量密度上產生后驗分布來調整模型大小,因此可以根據數據自適應聚類個數,其中狄利克雷過程混合模型是最常用的貝葉斯非參數模型之一[16?18].Figureoa 等[19]提出了一種物理一致的貝葉斯非參數混合模型,該方法可以自動估計最佳的混合分量個數,并且將相似性測度融入先驗信息,提高了復現和泛化的精度.但是該方法使用吉布斯采樣計算模型的后驗概率,計算復雜度較高.

鑒于SEDS 存在的上述缺陷,本文提出了改進的SEDS (Improved SEDS,i-SEDS).該方法有效地解決了SEDS 中穩定性和精度無法兼顧的問題,并且可以自動確定合適的分量個數.仿真以及Franka-panda協作機器人的實驗結果驗證了本文方法的有效性和優越性.本文的主要貢獻有:1)使用狄利克雷過程高斯混合模型(Dirichlet process GMM,DPGMM)代替GMM 擬合演示,并利用變分推斷(Variational inference,VI)訓練模型,該模型可以根據演示數據自動確定合適的混合分量個數.仿真分析超參數對DPGMM 的影響,為超參數的選擇提供了指導意義;2)采用參數化的李雅普諾夫函數修改了原SEDS 中的穩定性約束條件,從而提高了學習軌跡的精度,解決了穩定性和精度難以兼顧的問題.

1 問題描述

將機器人離散運動公式化為由自治動態系統驅動的控制律.考慮一個狀態變量ξ∈Rd,ξ通常表示笛卡爾空間中末端執行器的坐標.有時ξ也可用于定義機器人系統的廣義坐標(例如,機械手的關節角度或輪式機器人的姿勢)

式中,f(ξ) 是一個非線性連續可微函數,用于編碼特定行為,例如拾取搬運物品,伸手拿杯子等.從初始位置ξ0開始,機器人運動ξt,t∈[0,+∞) 由式(1)積分得到,運動最后收斂至單一吸引子ξ?,f(ξ?)0.本文需要估計該吸引子上全局漸近穩定的動態系統f(ξ).

通常,將基于一組M條演示軌跡的數據對f(ξ) 進行估計,Tm表示第m條演示軌跡的序列長度,估計得到的DS 為一般采用回歸算法進行估計,如高斯過程回歸[20]、局部加權映射回歸算法[21]和混合高斯回歸等.但這些標準的回歸技術在訓練過程中沒有考慮DS 的漸近穩定性,很可能是不穩定的或收斂至偽吸引子.因此SEDS 方法將不穩定DS 的建模轉換為非線性優化問題,構造了全局穩定的運動估計,具體流程如圖1 所示.

圖1 基于SEDS 的機器人示教學習流程圖Fig.1 Flow chart of LfD based on SEDS

上述方法有足夠的靈活性來建模各種運動,但是無法確保DS 的漸近穩定性,為此,SEDS 給出了在保證系統穩定性下的參數學習方法,即通過最小化帶非線性項約束的目標函數來估計參數 Θ.

式中,?0表示矩陣的負定,是全部訓練數據的總數量.目標函數J(Θ) 的選取有均方誤差(Mean square error,MSE) 和對數似然(Log likelihood,LL)兩種.

式中,對數ln 也可換成以其他常數為底的對數,上式的約束是全局穩定收斂的充分條件,這些條件由Lyapunov 第二穩定性方法推導得到,見定理1.

定理1.如果存在徑向無界且滿足式(5) 的Lyapunov 函數V(ξ):RdR,則DS 在ξ?點處全局漸近穩定.

SEDS 方法可以有效地從演示中估計出具有全局漸近穩定性的DS,是LfD 領域中的常用方法,但是該方法存在兩個問題:1) 用于估計初始DS 的GMM-GMR 方法需要人工指定混合分量個數K,當狀態ξ維度升高或演示軌跡變得復雜時,通過經驗確定超參數K將變得很困難;2)在SEDS 中,V(ξ)是二次李雅普諾夫函數(Quadratic Lyapunov function,QLF),即V(ξ)(ξ ?ξ?)T(ξ ?ξ?).在幾何學上,QLF 只允許L2范數(即 ‖ξ ?ξ?‖2)距離是單調遞減的軌跡[11].這導致了SEDS 在包含高曲率或非單調(暫時遠離吸引子)的高度非線性運動中表現不佳,不能同時保證穩定性和精度性.

針對問題1),本文利用貝葉斯非參數模型能根據數據自動確定最佳聚類個數的特性,采用了DPGMM 擬合演示數據,并推導GMR 估計初始DS;針對問題2),本文選擇參數化QLF (Parametrized QLF,P-QLF)來確保估計DS 的穩定性,即V(ξ)(ξ ?ξ?)TP(ξ ?ξ?).其中P的作用是將簡單的QLF重塑為“橢圓”形式,放松了約束條件,從而能夠精確復現不收縮(高曲率且朝向目標具有非單調性)的演示軌跡.

2 DPGMM-GMR 算法

DPGMM-GMR 算法由DPGMM 的建模過程、利用變分推斷進行模型求解和推導GMR 估計初始DS 三部分組成.

2.1 狄利克雷過程高斯混合模型

狄利克雷過程(Dirichlet process,DP)一般用DP(G0,α)表示,其中G0是連續的基分布,α是集中參數,用來控制從DP 中抽取的分布的離散化程度[22].假設從DP 中隨機抽取一個樣本分布G,然后再從G中獨立地抽取N個隨機變量

通過SBP,可以將獨立于G0繪制的原子θk視為混合模型分量的分布參數,該模型包含無限數量的分量,并且每個分量的權重為πk(v),從而建立了狄利克雷過程混合模型.

式中,Cat(·) 表示分類分布.

在狄利克雷過程混合模型的基礎上明確定義基分布G0為Normal-Wishart 分布,即θk～NIW(θ0),就得到了DPGMM,這意味著每個高斯分量的均值和精度都服從一個獨立的Normal-Wishart 分布,根據式(8),DPGMM 的公式化表示如下:

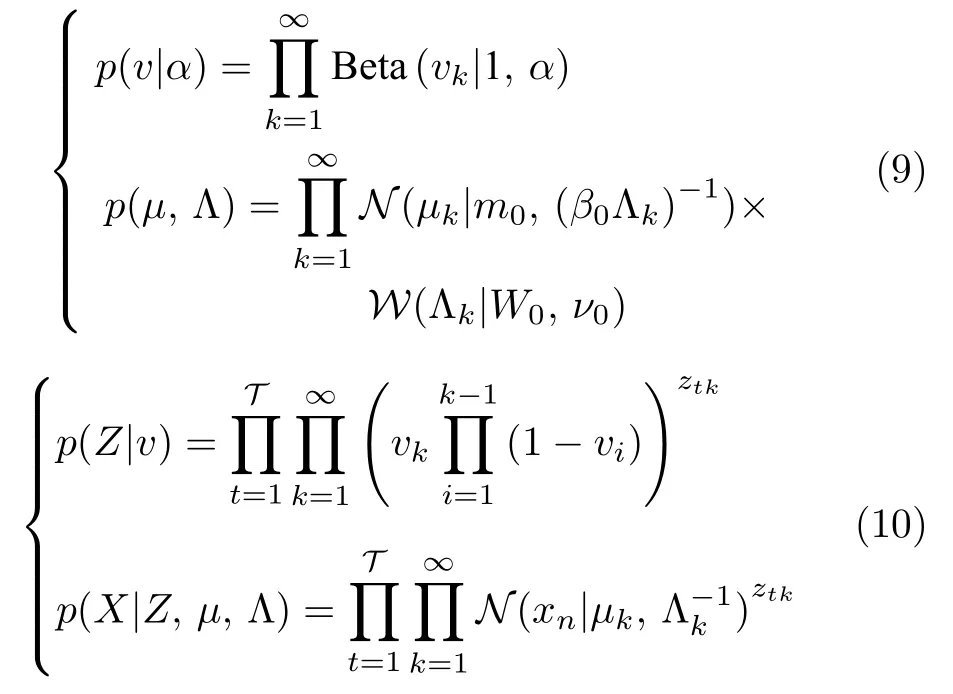
式中,μk和Λk分別表示第k個高斯分量的均值和精度,m0和β0分別是μk的高斯先驗的均值和方差,W0和ν0分別是 Λk的Wishart 先驗的精度矩陣和自由度.

式(9)是給定的共軛先驗分布,式(10)是模型的似然函數.DPGMM 的概率結構如圖2 所示.然而在無限維的設定下,實際中模型不易處理.因此本文采用一種常見的策略,即基于DP 的截斷SBP[24].預定義最大的混合分量數,并且令即對于所有k >,πk(v) 等于零.

圖2 DPGMM 概率結構圖Fig.2 DPGMM probability structure diagram

2.2變分推斷

第2.1 節已為所有隨機變量明確定義了共軛先驗和模型的似然函數,本節采用變分貝葉斯方法得出參數可靠的后驗分布.將隱變量和未知參數表示為 Θ{v,Z,μ,Λ},超參數表示為Ξ{α,m0,β0,W0,ν0}.由于實際后驗p(Θ|X,Ξ) 難以計算,因此變分推斷方法引入任意分布q(Θ) 以逼近p(Θ|Ξ,X).在此假設下,導出模型的對數似然值 lnp(X),即:

其中

KL(q||p)表示變分后驗q(Θ) 和實際后驗p(Θ|X,Ξ)之間的KL(Kullback-Leibler)散度,刻畫了兩個分布之間的相似程度.為降低求解難度,一般采用平均場理論限制概率分布q(Θ) 的范圍,然后尋找這個類別中使得KL 散度最小化的概率分布[25].因此需要將q(Θ) 分解為:

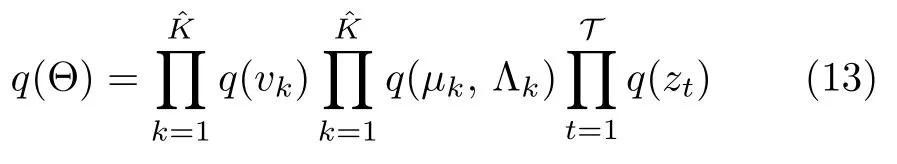
同時,考慮DPGMM 的共軛先驗配置,根據共軛的定義,期望后驗q(Θ) 與先驗p(Θ) 具有相同的函數形式[26],可得:

指示變量zt滿足[27]:

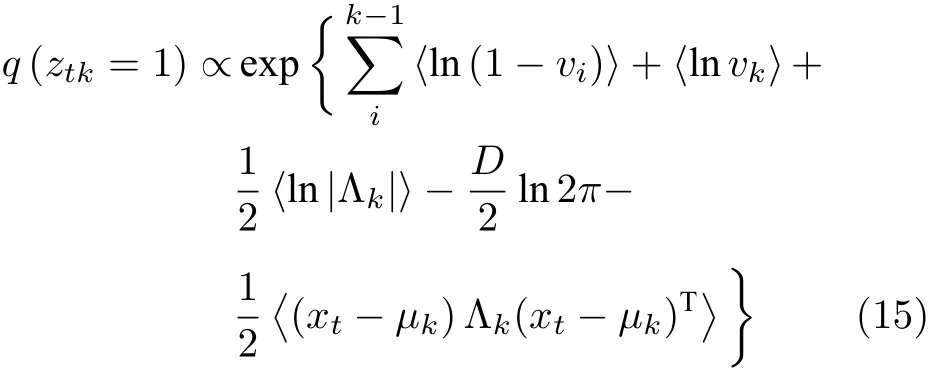
式中,〈·〉表示數學期望.

采用變分貝葉斯期望最大化(Expectation maximization,EM)算法.對該模型參數進行迭代求解.該算法類似于EM 算法,在E 步中,計算指示變量的期望;在M 步中,該期望值用于重新計算其他參數的變分分布.

期望通過變分推斷得到DPGMM 模型參數的后驗分布后,可以得到如下的模型聯合概率密度:

式中,St(·)是學生t分布,各分布的權重πk(v) 按下式計算:

式中,〈vk〉1/(1+α).

2.3 GMR 估計初始DS

與基于GMM 的GMR 一樣,先對式(16)的DPGMM 中的均值和方差進行劃分.

給定輸入位置ξt下輸出速度的條件概率分布為:

其中

DPGMM 在擬合演示軌跡時,自動確定最佳分量個數K,其余不相關高斯分量權重趨向于0,因此可以丟棄πk(v)〉 值過低的高斯分量來簡化計算.同時將式(20a)代入式(21)得到動態系統估計.

3 基于P-QLF 的穩定DS 估計

第2 節利用DPGMM-GMR 從演示中估計初始動態系統同其他的回歸算法一樣,訓練得到的不具有全局穩定性.SEDS 方法針對該問題構造了具有穩定性約束的非線性規劃問題,如式(3)所示.其不等式約束Ak+(Ak)T?0 通過QLF 推導得到,作為DS 穩定收斂的充分條件,該約束過于嚴格,導致學習的DS 為了確保穩定性而使生成的軌跡偏離了演示,尤其是面對不收縮(高曲率且朝向目標具有非單調性)的演示軌跡.本節使用PQLF 代替QLF 進行穩定性約束的推導,從而解決SEDS 中存在的穩定性和精度無法平衡的問題.

P-QLF 通常用于確保線性時不變(Linear timeinvariant,LTI)系統的穩定性,如命題1 所述.

命題1.形式為+b的線性DS 在吸引子ξ?處全局漸近收斂,當且僅當:

證明.見文獻[19].

命題1 易擴展到式(22)表示的線性參數可變系統中,即Ak為LTI 參數,混合系數hk(ξ) 是狀態相關的時變參數.如命題2 所述.

命題2.式(22)中定義的非線性DS 在吸引子ξ?處全局漸近收斂,當且僅當

式中,P為對稱正定矩陣.

證明.如果存在連續且可微的李雅普諾夫函數V(ξ)滿足定理1,即可證明命題2.通過考慮以下形式的P-QLF 候選函數:

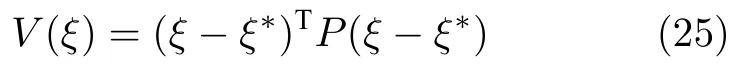
由于其二次形式,可以確保V(ξ)>0,第2 個條件是取V(ξ) 的時間導數:

將ξξ?代入式(25)和(26),可以確保V(ξ?)0,0.因此,如果滿足條件(24),則式(22)相對于吸引子ξ?是全局漸近穩定的.□

不難發現式(4)的約束條件是式(24)的一種特殊情況,即當P為單位矩陣時,式(24)就等同于式(4).SEDS 中穩定性和精度的兩難問題本質上是因為穩定性約束過于嚴格,使得可行的參數空間無法滿足精度要求.而基于P-QLF 推導得到的穩定性約束放松了對P的限制,只要滿足P為對稱正定矩陣即可,從而擴展了原問題的可行域.解決了SEDS學習不收縮軌跡時精度過低的問題.

4 實驗

仿真實驗在人類手寫數據庫(LASA 數據集)和Franka-panda 機器人上進行,實驗結果驗證了本文提出方法的有效性.

4.1 DPGMM-GMR 算法性能分析

盡管利用DPGMM 對演示進行擬合可以自動確定合適的聚類個數,但該方法引入了更多的超參數 Ξ{α,m0,β0,W0,ν0}.因此需要研究這些超參數對模型性能的影響,從而來指導超參數的選擇.訓練數據從LASA 數據集(該數據集是二維平面手寫軌跡數據)中隨機選取10 組演示.ξ表示二維笛卡爾位置,即ξ{ξ1,ξ2},演示數據集合X通常根據對稱性,超參數m0會選擇為X的均值.而超參數W0是一個 4×4 的矩陣,難以對所有矩陣元素進行分析,因此令W0ω×I,其中ω為縮放系數,是一個正標量.I是 4×4 的單位矩陣.只需要對α、β0、ω、ν0四個標量超參數進行研究.對10 組演示訓練得到10 個DPGMM,用對數似然值給模型打分,數值越高則說明模型擬合效果越好.10 個模型的對數似然值相對于各個超參數(固定其他超參數只變化一個超參數)的變化趨勢如圖3 所示.由圖3 可以看出:1)模型對于超參數的變化不敏感,一般ν0取數據維數即可,β0和ω取值不宜過大,α對模型影響最大,但只有在lnα>2時似然對數值才發生明顯下降;2)對于任意一個超參數,10 個模型的對數似然值對于該超參數具有相同變化趨勢,這意味著DPGMM 超參數具有可復用性,一組超參數能夠適用于相同場景下的不同演示數據集,例如LASA 數據集,同一個機械臂操作空間下的不同任務演示等.DPGMM 超參數的不敏感性和可復用性使其在實際任務中的使用更加便捷.

圖3 DPGMM 對數似然值關于超參數的變化趨勢Fig.3 The change trend of DPGMM log-likelihood value on hyperparameters

接著,在整個LASA 數據集上定量評估基于VI 的DPGMM-GMR 算法擬合初始DS 的效果,超參數均設置為αβ0ω1,ν04.對比算法包括基于貝葉斯信息準則的GMM-GMR (EM 算法)、狄利克雷分布GMM-GMR (VI)和DPGMM-GMR,其中貝葉斯信息準則高斯混合模型最大評估分量設定為15 個,其余方法的截斷分量也設置為15.性能指標采用以下形式均方根誤差(Root mean square error,RMSE):

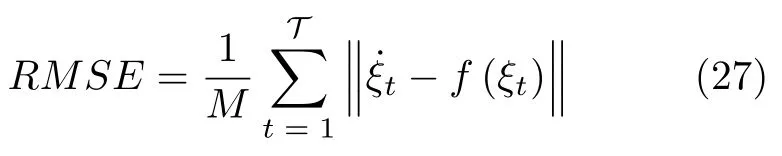
式中,M和T分別表示一組演示中軌跡的條數和所有的軌跡點個數.

4.2 i-SEDS 學習方法性能分析

本節i-SEDS 的性能分析同樣在數據集LASA上進行,如果算法能夠使復現的軌跡緊密(準確)地跟隨演示軌跡,則表明該算法可以令人滿意地解決穩定性和精度的難題.

由圖4 可以看出,所有復現軌跡緊密跟隨了演示軌跡,仿真結果說明了i-SEDS 的有效性.圖5給出了SEDS 和i-SEDS 在部分不收縮軌跡上的復現結果.可以看出,SEDS 生成的軌跡完全偏離了演示,這是由于遵循QLF 穩定性結果導致的.圖5定性地說明了i-SEDS 可以較好地解決SEDS 穩定性和精度的難題.

圖4 i-SEDS 方法在LASA 數據集上的復現效果Fig.4 The reproductions of i-SEDS method on LASA dataset

圖5 SEDS 和i-SEDS 在不收縮軌跡上的復現結果Fig.5 i-SEDS and SEDS reproductions on the non-contractive demonstrations

為了定量分析該方法的有效性,使用文獻[28]提出的掃描誤差區域(Swept error area,SEA).SEA 方法計算了演示軌跡和復現軌跡之間的面積,計算公式如下:

圖6 掃描誤差區域(SEA)示意圖Fig.6 Schematic diagram of Swept error area (SEA)

考慮到原始SEDS 中2 種不同的目標函數MSE 和LL,以及i-SEDS 在學習不收縮演示軌跡時具有明顯優勢.因此利用SEA 方法定量分析i-SEDS (MSE)、i-SEDS (LL)、SEDS (MSE)、SEDS(LL)四種方法分別在收縮和不收縮演示軌跡上的性能.從LASA 數據集中取收縮軌跡和不收縮軌跡各10 組,分別使用上述4 種方法學習穩定DS,計算相應的SEA,結果如結果如圖7所示.從圖7(a)可以看出,四種方法的SEA 在收縮軌跡上差別并不明顯,i-SEDS 僅略優于SEDS 方法.但在不收縮軌跡組的圖7(b)中,i-SEDS 方法的復現精度要明顯優于SEDS 方法.基于LL 的方法精度要略高于MSE,但MSE 的計算速度更快,因此,在實際使用中可以根據需求進行選擇.

圖7 4 種方法在收縮和不收縮軌跡上的SEA 分析Fig.7 Performance analysis of four methods on contraction and non-contraction demonstrations with SEA

4.3 機器人實驗

為了驗證本文方法的有效性,在7 自由度的機械臂Franka-panda 機器人上進行了實驗驗證.

機器人實驗是在操作空間中學習物塊搬運任務,如圖8 所示.這是一個點到點運動的任務,機械臂需要學會如何從機械臂初始位置到達物塊放置位置,然后拾取物塊將其放入目標容器中,整個過程由拾取物塊?放置物塊2 部分組成,并利用Kinect 攝像頭對物體進行跟蹤.

圖8 物品搬運任務示教流程圖Fig.8 The process of object transport task teaching

1)示教:首先設置panda 機械臂為示教模式,再由演示人員拖動機械臂完成拾取物塊?放置物塊2 個步驟,整個示教過程如圖8 所示.然后不斷調整物塊起始位置重復上述示教過程共8 次,同時以10 Hz頻率記錄機械臂末端位置和速度,獲取8 條演示軌跡數據,記作

2)學習:在對演示軌跡建模前,需要對數據進行一些預處理.a)軌跡平滑:使用移動均值濾波對采集到的演示數據進行平滑處理.b)任務分割:為了降低任務的學習成本,將物品搬運任務分解成拾取物塊?放置物塊2 個子任務.根據2 個子任務切換過程中機械臂末端速度為零這一特點將演示軌跡分成2 段,然后各自進行學習.c)目標位置原點化:為保證動態系統的參數不會隨目標位置的變化而變化,需要將參考坐標系的原點設在目標位置處.2 個子任務的演示軌跡都轉化為以原點為終點的軌跡.預處理后的演示軌跡如圖9 所示.

圖9 預處理后的物品搬運任務的演示軌跡Fig.9 Preprocessed demonstrations of object transport task

使用i-SEDS 方法對預處理后的演示數據進行建模,用于2 個子任務學習的超參數均設置為α0.1,β0ω1,ν06.

3)復現.機械臂從初始位置開始,通過模型不斷迭代得到當前位置下的期望速度將其作為逆運動學的輸入驅動機械臂按照期望軌跡到達目標位置.記錄每次生成的軌跡,獲得的結果如圖10 所示.所有復現軌跡都與演示具有相似的位置和速度輪廓,說明兩者均遵循相似的動力學.

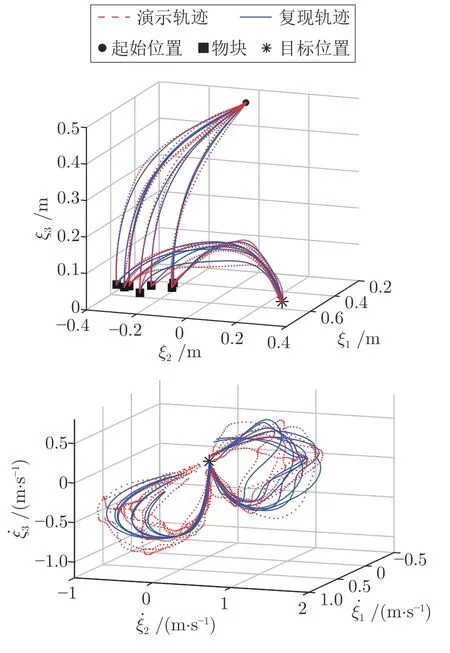
圖10 物品搬運任務復現位置和速度軌跡Fig.10 Position and velocity trajectories of reproduction in object transport task

a)目標位置的變化.圖11 顯示了模型對環境變化的魯棒性,其中虛線表示原始復現軌跡,實線表示在t4 s 時對目標位置進行轉移后由動態系統重新規劃的軌跡,可以看到該模型可以快速適應目標位置的變化,重新規劃軌跡使機械臂到達目標.

圖11 機械臂運行時改變目標位置后的軌跡變化Fig.11 Trajectory changes after moving the target container when the robot arm is running

b)抗擾動能力.圖12 顯示了模型對外界擾動的魯棒性,在t4 s 時,施加擾動使機械臂脫離原始軌跡,其中虛線表示原始軌跡,實線表示機械臂在脫離原始軌跡后模型重新規劃的軌跡,可以看到機械臂在受到外界擾動后仍能平穩到達目標位置,因此該模型具備一定的抗擾動能力.

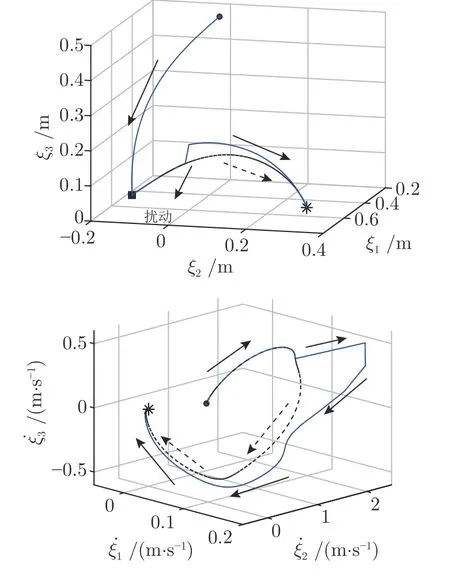
圖12 對機械臂施加外界擾動時的軌跡變化Fig.12 Trajectory changes when external disturbance is applied to the robot arm

上述機器人實驗展示了i-SEDS 方法在確保穩定性的前提下,仍具有良好的復現精度以及泛化能力和抗擾動能力.

5 結束語

本文分析了SEDS 方法中存在的缺陷,并給出了合理的解決方案.首先利用DPGMM 對演示數據進行擬合,并使用變分推斷求解模型參數,推導GMR 擬合初始DS.解決了基于EM 算法的GMM難以確定混合分量個數的難題.然后利用P-QLF推導新的寬穩定性約束取代原有約束,最后結合目標函數優化得到能精確復現的穩定DS.在LASA數據集中驗證了DPGMM 超參數的性質和其推導的GMR 算法的性能,以及i-SEDS 方法在不收縮軌跡上的優越性能.最后通過Franka-panda協作機器人上的實驗,驗證了本文方法在實際場景的有效性.在未來工作中,將降低本文方法模型的復雜度.