污水處理過程遞推雙線性子空間建模及無模型自適應控制

張 帥 周 平

活性污泥法是目前使用最為廣泛的污水處理方法,其工藝流程如圖1 所示.由污水管網收集的污水首先經過格柵、洗砂間、初沉池等工序去除碎石、砂子等固體懸浮物;然后,污水在生化池內通過厭氧反硝化作用和好氧硝化作用,分解有機氮和氨氮,去除大部分污染物;最后,經過生化反應處理的污水在二沉池內進行二次沉淀,進一步提高水質,從而排入收納河道.圖1 所示污水處理過程中,生化池厭氧區第二單元硝態氮濃度SNO,2和好氧區第五單元溶解氧濃度DO,5是關乎出水質量優劣的最重要過程變量[1?3].其中DO,5受控于五區溶解氧轉換系數KLa,5,SNO,2受控于由五區回流至二區的內回流流量Qa,因此它們之間有著較強的耦合性,這在一定程度上增加了SNO,2和DO,5建模和控制的難度.同時,由于生化反應過程的時變性、不確定性和復雜性,使得SNO,2和DO,5的機理建模和基于模型的控制難以實現.

圖1 污水處理工藝流程圖Fig.1 Wastewater treatment process

目前,針對難以建立機理和經驗模型的復雜工業過程,數據驅動子空間辨識方法得到了越來越廣泛的應用[4?8].子空間辨識技術不需要系統的先驗知識,可直接利用輸入輸出數據,通過統計、優化和線性代數的思想得到系統的動態模型,可有效避免傳統建模過程代價昂貴、計算復雜、應用范圍較窄的缺點,因而具有普遍的適用性和應用價值[9?10].目前,子空間辨識在污水處理過程中的應用主要集中于離線或線性子空間辨識建模[6,11],而污水生化反應過程是一個典型的時變、非線性過程;因此,基于線性子空間辨識的污水生化過程建模和控制效果存在一定的局限性.為此,本文采用一種遞推最小二乘雙線性子空間辨識方法,建立污水生化池SNO,2和DO,5的具有參數自適應能力的數據驅動遞推雙線性模型,以更好地捕捉污水處理過程的非線性時變動態特性.

近年來,針對污水處理過程SNO,2和DO,5的控制問題,基于數據驅動的控制策略引起了廣泛關注,如基于數據驅動的自適應神經網絡控制[12]、模糊神經網絡控制[13?14],神經網絡模型預測控制[15?16]等.這些方法雖然可以在不使用精確數學模型的條件下實現SNO,2和DO,5的自適應控制,但污水生化反應過程的模糊規則建立困難,神經網絡模型則需要大量的污水運行數據進行訓練.此外,預測控制在每一時刻都要求解一個非線性約束優化問題,計算成本較高.同時,上述算法控制器的設計依賴于模糊規則或神經網絡訓練模型,因此基于模型的控制器設計中的未建模動態等問題依然存在.其他在實際系統中應用較好的數據驅動控制和自適應控制方法,如文獻[17]事件驅動下的自學習最優調節控制和文獻[18]自適應非線性魯棒控制,同樣存在未建模動態等與上述方法中相同的問題.在這種背景下,針對污水處理過程研究直接數據驅動控制的無模型自適應控制(Model-free adaptive control,MFAC)具有十分重要的意義.MFAC 于1994 年由侯忠生教授首次提出[19],并在后期不斷發展和完善[20?25],現已形成一套新的針對非線性動態系統的控制理論與方法.MFAC 利用非線性系統的輸入輸出數據以及動態線性化技術[26],在受控系統的每個工作點處,建立虛擬動態線性化數據模型,然后基于此虛擬模型設計加權一步向前控制器.整個控制器設計過程僅依靠輸入輸出數據和動態線性化技術,不需要過程先驗知識和系統模型的參與,且控制器結構簡單、計算方便,可有效解決未建模動態問題.

綜上所述,本文針對污水處理過程難以機理建模和直接數據驅動控制的問題,采用一種改進的MFAC 方法,研究污水處理過程SNO,2和DO,5的直接數據驅動控制.由于MFAC 控制器待調參數眾多,且參數的取值直接影響控制系統的性能指標,為改善MFAC 控制器參數的調整效率,提高MFAC控制器性能,采用基于蒙特卡羅(Monte Carlo)實驗的多參數靈敏度分析(Multi-parameter sensitivity analysis,MPSA)和遺傳粒子群優化(Genetic algorithm?particle swarm optimization,GAPSO)方法整定控制器待調參數,對常規MFAC 方法進行改進,完成的主要工作如下:

1) 由于在控制器參數的整定過程中,需要基于污水處理過程做數千次Monte Carlo 實驗和數百次優化計算,而基于實際污水處理系統的參數整定實驗代價高昂,BSM1 (Benchmark simulation model No.1)標準模型[27]運行又較為復雜.因此,利用一種遞推雙線性子空間辨識(Recursive bilinear subspace identification,RBLSI)方法,建立污水處理過程SNO,2和DO,5的RBLSI 模型,與遞推線性子空間辨識(Recursive linear subspace identification,RLSI)的模型測試效果對比后,選擇效果更優的RBLSI 模型作為MFAC 控制器參數整定的被控對象模型.

2) 采用緊格式動態線性化無模型自適應控制(Compact form dynamic linearization MFAC,CFDL-MFAC)的方法,設計SNO,2和DO,5的CFDL-MFAC加權一步向前控制器;基于SNO,2和DO,5的遞推雙線性子空間模型,開展SNO,2和DO,5的CFDL-MFAC控制器待調參數靈敏度分析的Monte Carlo 實驗,并采用MPSA 方法,依據實驗結果選出控制器的敏感參數.

3) 為不敏感參數取適當的值,以敏感參數為優化變量,采用GA-PSO 優化算法,做CFDL-MFAC控制器敏感參數的優化整定實驗.

4) 將控制器參數整定的結果作用于CFDLMFAC 控制器,開展污水處理過程SNO,2和DO,5的設定值跟蹤和干擾抑制的控制實驗研究,以充分驗證所提方法的有效性和先進性.

本文基于多參數靈敏度分析(MPSA)和遺傳粒子群優化(GA-PSO)算法的無模型自適應控制(MFAC)方法在硝態氮和溶解氧濃度的控制中具有以下優勢.首先,控制器的設計僅需污水系統的Qa和KLa,5數據以及SNO,2和DO,5數據,不需要污水系統的模型信息,可避免傳統的未建模動態問題的存在,非常適用于污水處理系統的實際應用.其次,本文算法控制器結構簡單、計算量小、控制器設計不需精確的污水模型,控制器計算成本較低.最后,本文方法可實現帶有參數變化的非線性污水處理系統SNO,2和DO,5濃度的直接數據驅動控制.因此,本文方法無論在污水處理的理論研究方面還是實際應用方面都具有重要意義.

1 SNO,2和DO,5 的遞推雙線性子空間建模

為更加精確地描述污水處理過程的非線性時變動態特性,為后期CFDL-MFAC 控制器參數靈敏度分析的Monte Carlo 實驗和優化整定實驗做好模型準備,首先采用帶有遺忘因子的遞推最小二乘技術,改進常規雙線性子空間辨識方法[28?29],建立SNO,2和DO,5的RBLSI 模型,并與文獻[7]中遞推線性子空間辨識(RLSI)建模方法做模型測試對比,根據兩種方法的模型測試結果及其對比分析,選擇效果更好的RBLSI 模型作為控制器參數Monte Carlo 實驗和優化整定實驗的被控對象模型,具體過程如下.

1.1 基于最小二乘的遞推雙線性子空間辨識建模

1.1.1 遞推雙線性子空間辨識矩陣構造

用如下形式的MIMO 雙線性系統描述污水處理生化池內SNO,2和DO,5的變化過程:

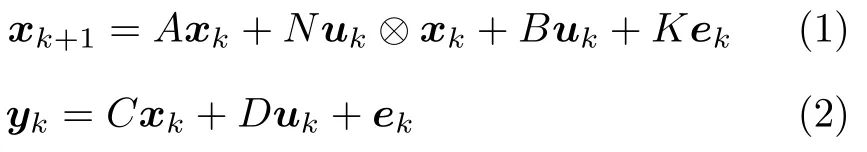
式中,uk∈Rm,yk∈Rl,xk∈Rn分別表示系統的輸入、輸出和狀態向量,ek表示獨立于輸入uk的零均值白噪聲序列,其方差E[ep,eq]Sδpq >0.A,B,C,D,K為具有適當維數的系統矩陣,N∈Rn×nm表示系統的雙線性特性矩陣,?表示克羅內克(Kronecker)積.

將式(2)中uk代入式(1),通過化簡,可將式(1)中uk ?xk項轉化為輸入和輸入以及輸入和輸出向量之間的Kronecker 積,由此得到如下具有線性系統結構形式的雙線性系統狀態空間方程:

由于式(3)和式(4)與線性狀態空間模型有著相同的結構形式,因此線性系統子空間辨識的一些原理也可應用于雙線性系統(3)和(4)的辨識.假定 {A,}能觀,{A,C} 能控,在不考慮噪聲影響前提下,將式(4)代入式(3),通過對輸出變量的前向迭代.可得類似于線性系統子空間辨識中的矩陣輸入輸出方程

式中,Up和Uf分別表示過去和當前時刻的輸入漢克(Hankel)矩陣,

Yp和Yf分別表示過去和當前時刻的輸出Hankel矩陣,其定義與上述Up和Uf的定義相似.和分別代表過去時刻和當前時刻的廣義輸入Hankel矩陣,其定義類似于Up和Uf的定義,只需將Up和Uf中的輸入向量uk(k0,···,2i+j ?2) 替換為式(3)中定義的廣義輸入向量(k0,···,2i+j ?2),便可得到和Xp,Xf分別表示過去和當前時刻的子空間狀態矩陣,其定義分別為

Γi,Δi分別表示廣義能觀和廣義能控矩陣,其定義分別為

1.1.2 遞推參數矩陣求解

將式(5)和式(7)代入式(6),在忽略噪聲影響的情況下,系統當前輸出Yf的行空間等價于過去輸入輸出Hankel 矩陣、當前輸入Hankel 矩陣以及過去和當前廣義輸入Hankel 矩陣行空間的組合,由此得到系統輸出Yf的預測方程為

1.2 SNO,2和 DO,5 的遞推雙線性子空間模型

將第1.1 節所述RBLSI 方法應用于污水處理過程SNO,2和DO,5的建模,以內回流流量Qa和五區溶解氧轉換系數KLa,5為控制變量,即u1Qa,u2KLa,5,u[u1u2]T,以SNO,2和DO,5為被控變量,即y1SNO,2,y2DO,5,y[y1y2]T,狀態向量x是輸入數據u和輸出數據y子空間矩陣的非線性組合,可由式(5)和式(7)求得.基于污水處理數據,建立SNO,2和DO,5的遞推雙線性子空間模型,并與文獻[7]中遞推線性子空間辨識(RLSI)建模方法做模型測試對比.

實驗共使用實際污水處理數據550 個,其中400 個為建模訓練用數據,150 個為模型測試用數據.由本文RBLSI 方法得到最終的SNO,2和DO,5預測模型結構如式(14)所示,基于最新一組數據得到的子空間參數矩陣為

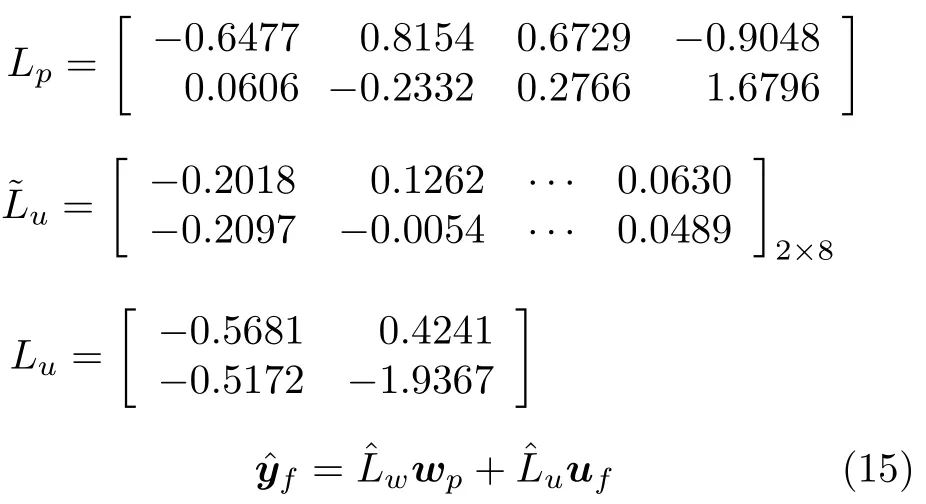
由文獻[7]算法得到的SNO,2和DO,5預測模型結構如式(15)所示,基于最新一組數據得到的子空間參數矩陣為

與式(14)描述的RBLSI 模型相比,式(15)描述的RLSI 模型在結構上缺少了這一部分,即未考慮到輸入、輸出數據向量的Kronecker 積對輸出預測的影響,對輸入、輸出數據的利用不充分,因此其預測效果相對于RBLSI 模型來說具有一定的保守性.

由預測模型表達式(14)和式(15),基于污水數據可得到兩種算法的模型測試曲線,如圖2 所示.由兩種算法實際的預測誤差,通過核心平滑密度估計技術,可得到兩種算法預測誤差的概率密度函數(Probability density function,PDF)形狀曲線,如圖3 所示.圖3 曲線服從高斯分布,使用數據擬合工具,通過核密度估計技術和高斯擬合算法,可得到文獻[7]的RLSI 算法和本文RBLSI 算法預測誤差的PDF 表達式,分別如式(16),(17)和式(18),(19)所示.

式中,ex代表相應變量的預測誤差,fpdf(ex) 表示對應該誤差的概率.

通過對比分析兩種算法的模型測試效果(圖2)、預測誤差PDF 形狀(圖3) 及測試均方根誤差(Root mean square error,RMSE) (表1)可知,在對SNO,2和DO,5的預測過程中,本文RBLSI 算法具有更加接近于真實值的預測輸出、形狀更好的預測誤差PDF 曲線以及數值更小的測試均方根誤差,因而能夠更加精確地描述SNO,2和DO,5的變化過程.所以,最終選擇RBLSI 模型作為CFDL-MFAC控制器參數靈敏度分析和優化整定實驗的被控對象模型.

圖2 不同算法 SNO,2和 DO,5 的模型預測效果Fig.2 Model prediction effects of SNO,2and DO,5 with different algorithms

圖3 不同算法 SNO,2和 DO,5 的預測誤差PDF 曲線Fig.3 Error PDF shapes of SNO,2 and DO,5 prediction with different algorithms

表1 不同算法的RMSE 比較Table 1 Comparison of RMSE based on different algorithms

2 SNO,2和 DO,5 的CFDL-MFAC 控制

本節首先給出了CFDL-MFAC 控制器的設計方法,設計了SNO,2和DO,5的CFDL-MFAC 控制器.其次,為提高控制器參數調整效率,基于1.2 節建立的RBLSI 模型,詳細介紹了采用MPSA 方法對CFDL-MFAC 控制器參數做Monte Carlo 實驗,并依據實驗結果選擇靈敏參數的過程.最后,描述了采用GA-PSO 方法對控制器靈敏參數做優化整定,并利用整定好的參數對SNO,2和DO,5濃度進行跟蹤控制的過程,整個系統的控制框圖如圖4 所示.圖4 中,①表示輸出信號流,② 表示輸入信號流,③表示CFDL-MFAC 控制器參數更新信號流,其中包含偽雅可比矩陣 Φ(k)的初值 Φ(0),④ 表示偽雅可比矩陣 Φ(k) 更新信號流.

圖4 控制系統框圖Fig.4 The control flow chart

2.1 CFDL-MFAC 控制器設計

假設污水處理SNO,2和DO,5控制過程的離散非線性輸入輸出方程為

式中,yk∈Rl,代表被控輸出SNO,2和DO,5,uk∈Rm代表控制輸入Qa和Ka,5,ny、nu分別表示系統輸出和輸入階次,f(·) 表示一個未知非線性向量函數.

2.1.1 緊格式動態線性化(CFDL)

由文獻[20,25]可知,SNO,2和DO,5的CFDLMFAC 控制器的設計需要滿足如下兩個假設.

假設 1[20,25].系統(20)中的非線性函數f(·) 對輸入u(k) 存在連續偏導數.

假設 2[20,25].系統(20)滿足廣義Lipschitz 條件,即在任意時刻k,若‖Δu(k)‖‖u(k)?u(k ?1)‖0,則 ‖Δy(k+1)‖‖y(k+1)?y(k)‖≤b‖Δu(k)‖,b是一個大于零的常數.

上述假設條件分別是對常規非線性控制系統設計和被控輸出變化率的典型約束,對實際污水處理系統來說,由于它滿足能量守恒定律,有限范圍內的輸入變化必然引起有限范圍內的輸出變化.因此,任意兩個時刻SNO,2和DO,5的輸出變化量與Qa和Ka,5的控制變化量之間,一定存在有界的系數關系.故污水處理系統滿足假設1 和假設2,由此可得如下引理.

引理 1[20,25].對SNO,2和DO,5非線性控制系統(20),若滿足假設1 和假設2,且在任意時刻k,‖Δu(k)‖0,則存在一個偽雅克比矩陣(Pseudo Jacobian matrix,PJM) Φc(k),可將系統(20)化為一種如下形式的虛擬CFDL 模型:

式中,Φc(k)∈Rl×m是一個時變、有界的參數矩陣.

2.1.2 控制器推導與偽雅可比矩陣(PJM)的估計

控制系統的首要目標是要控制SNO,2和DO,5的濃度跟隨其設定值,保證污水處理系統的順利運行,提高出水水質;同時,考慮到如果相鄰兩個時刻控制增量過大會引起系統輸入劇烈跳變,增加執行機構的負擔,因此,以SNO,2和DO,5跟蹤誤差的二范數以及控制增量的加權二范數作為控制器推導的目標函數.

式中,yr表示系統輸出SNO,2和DO,5的目標值,λ為權重因子,λ>0.

將虛擬模型(21)代入目標函數(22),并對輸入u(k)求偏導,令其偏導數為零,得到SNO,2和DO,5的加權一步向前控制器

式中,ρ代表為避免求逆運算引入的步長因子,0<ρ ≤1.

由控制器(23)可知,CFDL-MFAC 算法的實現依賴于偽雅可比矩陣 Φc(k),而 Φc(k) 是一個未知、時變的參數矩陣,因此需要利用SNO,2和DO,5控制系統的輸入輸出數據對 Φc(k) 進行實時估計.考慮如下 Φc(k) 估計的目標函數:

對目標函數(24),關于 Φc(k) 求極值,得到Φc(k)的估計式為

式中,0<η ≤2 表示為避免求逆運算引入的步長因子.

由于SNO,2和DO,5模型是一個典型的時變系統,參數變化較大,為了使偽雅克比矩陣的估計式(25)能夠更好地跟蹤SNO,2和DO,5控制系統的時變參數,引入以下算法重置機制:

至此,式(23),(25) 和式(26) 組成SNO,2和DO,5控制系統的CFDL-MFAC 控制方法.其穩定性的證明與文獻[20,25]中基本相同,此處不再贅述.假設CFDL-MFAC 控制器求解時間為t0,則該算法控制時間復雜度為 O(t0).而對基于神經網絡模型的預測控制而言,若求解非線性約束優化問題時間為t1,預測時域為P,則其控制時間復雜度為O(P ×t1).此外,預測控制中非線性約束優化問題一般采用SQP 方法求解,需要一個基于變尺度法的迭代過程,而本文算法控制量求解僅需簡單的矩陣運算即可,因此其控制量求解時間t0要小于非線性約束優化問題的求解時間t1,這在第3.2 節實驗結果所得的控制量平均求解時間上也得到了驗證.因此本文CFDL-MFAC 算法控制環節的時間復雜度要低于基于神經網絡的模型預測控制.

2.2 CFDL-MFAC 控制器靈敏參數的選擇和遺傳?粒子群優化整定

由第2.1.2 節可知,SNO,2和DO,5控制系統的CFDL-MFAC 控制算法共有包含PJM 初值在內的11 個待調參數,而且并沒有MFAC 算法應用于實際污水處理過程的先例,參數的選取毫無經驗可循,這給控制器參數調整帶來極大的不便.為此,引入CFDL-MFAC 控制器參數的靈敏性分析算法和參數優化整定算法,對常規CFDL-MFAC 算法進行改進.首先,采用文獻[30]所描述的MPSA 算法,分析CFDL-MFAC 控制器參數的靈敏度,根據每個參數的累計頻率曲線分離程度(Degree of separation,DS)選出對控制器性能較為敏感的參數,以降低參數優化的復雜度;然后,采用GA-PSO 算法對敏感參數做優化整定,得到靈敏控制器參數的優化解;有效改善了控制器參數的調整效率,提升了控制器的性能.

2.2.1 CFDL-MFAC 控制器參數靈敏度分析

為選出CFDL-MFAC 控制器的靈敏參數,以第2.1 節CFDL-MFAC 控制算法控制第1.2 節SNO,2和DO,5遞推雙線性系統,以滿足控制器參數范圍的N組服從均勻分布的隨機參數集驅動CFDL-MFAC 控制器,將控制時長為T的SNO,2和DO,5的累計跟蹤誤差平方和作為損失函數指標,在該損失函數的基礎上,做Monte Carlo 實驗.

損失函數的計算式為

式中,para(λ,μ,η,ρ,b1,b2,α,φii(0),φij(0)) 表示控制器的待調參數,表示在控制器(23)作用下SNO,2和DO,5遞推雙線性系統的輸出,yr(k)表示的設定值,T表示控制時長.待調參數para中各控制器參數的約束范圍依次為

依據式(27)計算得到的N個損失函數值的數值大小,將其對應的參數集分為可接受參數集和不可接受參數集.考察每個參數在兩個參數集中的分布情況,若某個參數在兩個參數集中分布情況相同,則該參數為不靈敏參數,反之,該參數是靈敏的.具體過程如下.

按式(29)計算某參數的累計頻率cfj

其中,vi表示第i個參數值在其對應的參數集中出現的頻數.

繪制每個參數的累計頻率曲線,按下式計算其分離程度DS:

2.2.2 CFDL-MFAC 控制器靈敏參數的GA-PSO優化

以式(31)為適應度函數,對控制器的靈敏參數進行GA-PSO 優化整定

式中,pi(i1,···,7)分別對應para中的前7 個控制器參數,g(·)為分段函數,滿足g(pi)|pi>00,g(pi)|pi≤01;K1,K2和K3為控制器參數的約束懲罰系數,其作用就是在任一參數不滿足約束條件時,在適應度函數值上增加一個較大的懲罰值,使該參數對應的優化解不能進入最優解空間,將式(27)和式(28)組合而成的靈敏控制器參數的約束優化問題轉化為無約束優化問題,使優化過程更加簡便.需要指出的是,在優化之前需根據靈敏度分析結果,將適應度函數(31)中不靈敏參數變量取為適當的固定值,并去除其對應的約束懲罰項.

雖然常用智能優化算法粒子群和遺傳算法均可應用于目標函數(31)的優化求解,但由于單一粒子群優化(Particle swarm optimization,PSO)算法[31?32]和遺傳算法(Genetic algorithm,GA)[33?34]易陷入早熟收斂和局部最優,為提高控制器參數優化的收斂速度和優化精度,將兩種算法相結合,采用收斂速度更快、優化精度更高的GA-PSO 混合優化算法,對敏感控制器參數做優化整定.GA-PSO 算法首先使用GA 對適應度函數進行遺傳優化,在達到設定精度或優化指定代數之后,將得到的最優種群作為后續PSO 算法的初始種群;然后,以PSO 算法繼續尋優,直到滿足終止條件,此時得到的最優解為控制器參數最優值.此算法繼承了GA 染色體變異的特點和PSO 算法粒子具有記憶功能的特點,可有效提升算法搜索能力和收斂速度.單獨GA 和PSO 算法的迭代過程可分別參考文獻[33?34]和文獻[31?32],GA-PSO 混合優化算法的具體實現步驟如下.

算法1.GA-PSO 混合優化算法

步驟1.初始化GA-PSO 算法的參數.

步驟2.對靈敏控制器參數變量進行實數編碼.

步驟3.根據式(31)選擇染色體,并對染色體進行交叉和變異操作.

步驟4.判斷是否達到指定代數或優化精度,若未達到,返回步驟2;若達到,則將得到的最優種群作為PSO 的初始化粒子種群.

步驟5.計算粒子群適應度值,并作出評價.

步驟6.更新粒子的位置和速度.

步驟7.判斷是否達到終止條件,若未達到,返回步驟5;若達到,則即得到最優控制器參數.

3 數據實驗分析

由于第1.2 節中已經完成SNO,2和DO,5的遞推雙線性子空間建模實驗,這里只需在第1.2 節所建立的SNO,2和DO,5遞推雙線性子空間模型的基礎上,完成SNO,2和DO,5控制過程的CFDL-MFAC控制器參數敏感性分析實驗和敏感參數優化整定實驗,然后對參數優化整定后的CFDL-MFAC 控制器做性能分析實驗即可.本文采用戴爾臺式電腦XPS 8930 進行實驗,其CPU 為:i7-8700 (6 核),內存:16 GB,顯卡:NVIDIA GTX1070 (獨立8 GB),操作系統為win10 64 位家庭中文版,實驗時采用軟件為MATLAB 2016b.

3.1 CFDL-MFAC 控制器參數靈敏度分析和優化整定實驗

基于污水處理數據,按照第2.2.1 節中所述的參數靈敏度分析方法,做SNO,2和DO,5的CFDL-MFAC控制器參數靈敏度分析實驗,Monte Carlo 實驗的次數N取5 000,得到的參數累計頻率分布情況如圖5 所示,其中實線對應某參數在可接受參數集內的累計頻率分布情況,虛線對應不可接受參數集內的累計頻率分布情況.由圖5 可知,控制器參數(8)～(11)在兩個參數集內的累計頻率分布曲線差別較大,其余控制器參數在兩個參數集內的分布曲線形狀較為接近,由此可初步判斷控制器參數(8)～(11)比較靈敏.

圖5 控制器參數累計頻率分布曲線Fig.5 Cumulative frequency distribution curve of controller parameters

用式(30)計算圖5 中各參數累計頻率曲線的分離程度DS,依據計算結果分析各參數的靈敏情況,并為不靈敏的參數取值.靈敏度分析結果如表2所示,由表中第4 列可選出對應DS 值較小的參數作為CFDL-MFAC 控制器的靈敏參數,即φ11(0),φ12(0),φ21(0),φ22(0),同時對不靈敏的參數給出固定值,如表2 第5 列.以式(31)為適應度函數,分別按第2.2.2 節的GA-PSO 混合優化算法、文獻[33]中的GA 和文獻[31]中的慣性權重線性遞減PSO算法對靈敏參數做優化整定實驗.GA-PSO 算法的參數設置如表3 所示,終止條件為連續180 次迭代適應度值誤差不超過0.002,或達到最大迭代次數300,則終止迭代.GA 和慣性權重線性遞減PSO算法的最大迭代次數均為300,其他參數值與表3中對應參數相同.

表2 CFDL-MFAC 控制器參數靈敏度分析結果Table 2 Sensitivity analysis results of CFDL-MFAC controller parameters

表3 GA-PSO 算法參數Table 3 GA-PSO algorithm parameters

圖6 給出了混合GA-PSO 優化過程、GA 優化過程和PSO 優化過程的收斂曲線.由圖6 可知,所提CFDL-MFAC 控制器靈敏參數的GA-PSO 優化終止于第281 次迭代,最優適應度值為fitopt2.100.而GA 優化至最大迭代次數300 時,最優適應度值為fitopt2.181,且算法仍未收斂.PSO 優化終止于第300 次迭代,最優適應度值為fitopt2.114.由此可見,在CFDL-MFAC 控制器靈敏參數的優化過程中,GA-PSO 算法無論在收斂速度還是優化精度上都要優于單獨的GA 算法和PSO 算法,因此,最終CFDL-MFAC 的敏感控制器參數的最優解為GA-PSO 算法的優化結果:φ11(0)0.0835,φ12(0)?0.3469,φ21(0)?0.6992,φ22(0)?0.0467.

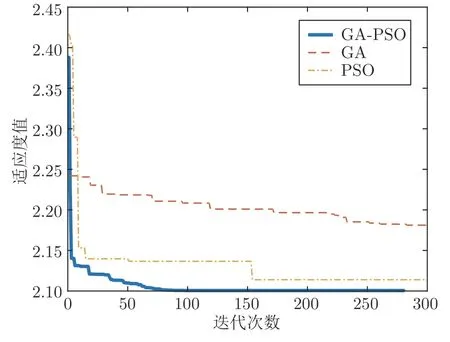
圖6 CFDL-MFAC 控制器靈敏參數優化收斂過程Fig.6 The optimization convergence process of sensitive parameter based on CFDL-MFAC controller

3.2 CFDL-MFAC 控制器性能分析實驗

采用控制器參數優化整定后的CFDL-MFAC控制器對污水處理過程SNO,2和DO,5的設定值做跟蹤控制實驗,實驗采樣間隔為0.25 h,實驗控制時長為62.5 h.實驗中,以跳變的階躍信號作為SNO,2和DO,5的跟蹤目標yr(k),以幅值為0.02 的隨機白噪聲序列描述污水處理過程存在的噪聲.同時,為考察改進CFDL-MFAC 控制器針對不同類型擾動的魯棒性,在系統輸出端分別施加幅值為0.1、周期為30 h 的方波擾動和幅值為0.15、周期為60 h 的正弦擾動,做CFDL-MFAC 控制器的抗擾性分析實驗.實驗時,方波擾動和正弦擾動在初始時刻即施加于系統SNO,2和DO,5的輸出值.跟蹤目標yr(k)的具體設置為

為進一步展現本文改進CFDL-MFAC 算法對SNO,2和DO,5的控制性能,在相同噪聲和擾動下,與文獻[7]中基于數據驅動的預測控制(Recursive bilinear subspace identification based model predictive control,RBL-MPC)算法進行比較.兩種算法在方波擾動和正弦擾動下的抗擾性控制結果對比如圖7 和圖8 所示,控制性能指標對比如表4 所示.由于實驗輸出與擾動變量數值不在同一數量級,為清晰地展現擾動變量對輸出值的影響,圖中擾動變量曲線均為加上輸出設定值之后的數值.

表4 不同算法控制性能對比Table 4 Comparison of control performance based on different algorithms

圖7 方波擾動抗擾性實驗Fig.7 Immunity test with square wave disturbance

圖8 正弦擾動抗擾性實驗Fig.8 Immunity test with sine disturbance

圖7 描述了在隨機噪聲和方波擾動的影響下,兩種算法對SNO,2和DO,5設定值的跟蹤效果.由圖7(a)可知,本文提出的改進CFDL-MFAC 算法雖然在方波擾動的切換處和跟蹤目標的跳變處有較大波動,但能在控制輸入的實際可操作范圍內,自適應地調整控制量的輸入值(如圖7(b)所示),并快速收斂于設定目標,完成對SNO,2和DO,5的穩定跟蹤,可有效抑制方波擾動信號的影響,而RBL-MPC 算法則無法在方波擾動下平穩地跟蹤SNO,2和DO,5的設定目標,抑制方波擾動的能力較差.此外,由兩種算法在方波擾動下的跟蹤誤差絕對值曲線圖7(d)可知,除部分設定值的跳變時刻和擾動信號幅值的切換處之外,RBL-MPC 方法的跟蹤誤差絕對值均大于本文CFDL-MFAC 算法,由此可進一步表明本文CFDL-MFAC 算法在SNO,2和DO,5跟蹤控制中的有效性和優越性.

由圖8 正弦擾動信號下的抗擾性實驗結果可知.在對SNO,2和DO,5的控制過程中,改進CFDLMFAC 算法能有效抑制外部正弦擾動的影響,實現對SNO,2和DO,5的精確跟蹤,且控制輸入滿足實際可操作范圍(如圖8(b)所示),而RBL-MPC 算法在正弦擾動下,雖然能實現對DO,5設定值的穩定跟蹤,但對SNO,2的跟蹤過程一直存在較大跟蹤誤差,無法實現對SNO,2和DO,5的同時跟蹤.兩種算法在正弦擾動下的跟蹤誤差絕對值曲線如圖8(d)所示,本文CFDL-MFAC 算法僅在個別設定值的切換處有較大波動,其余時刻的誤差絕對值均趨于零,而RBL-MPC 方法的跟蹤誤差則一直存在較大波動,且除少數設定值的切換時刻外,其跟蹤誤差絕對值均大于本文CFDL-MFAC 算法的跟蹤誤差絕對值.由此可見,本文CFDL-MFAC 算法在污水處理SNO,2和DO,5控制中的跟蹤效果要優于RBL-MPC 算法.

由上述SNO,2和DO,5的設定值跟蹤和抗擾性控制實驗的對比分析可知,與RBL-MPC 方法相比,本文提出的改進CFDL-MFAC 算法不僅控制性能更加精確(見表4 第3 行和第4 行),控制量求解速度更加迅速(RBL-MPC 方法控制量求解時間數量級為 10?2s,而CFDL-MFAC 算法控制量求解時間數量級為 10?5s,見表4 第2 行),且具有較強的抑制外部干擾的能力.兩種算法具體的控制性能指標可由表4 所知.

4 結束語

針對污水處理過程SNO,2和DO,5難以機理建模和直接數據驅動控制的問題,本文提出一種改進CFDL-MFAC 污水處理過程控制方法,即在傳統CFDL-MFAC 算法的基礎上,引進控制器參數靈敏度分析和GA-PSO 優化整定機制,采用MPSA 方法分析控制器參數的靈敏度,并使用GA-PSO 混合優化算法對敏感控制器參數做優化整定,以改進傳統CFDL-MFAC 算法控制器參數的調整效率,提高控制器的控制性能.同時,為便于進行靈敏度分析的Monte Carlo 實驗和靈敏參數的GA-PSO 優化整定實驗,采用一種RBLSI 建模方法,建立SNO,2和DO,5的遞推雙線性子空間模型,為參數優化整定實驗和控制器性能分析實驗提供較為精確的被控對象模型.基于污水處理數據的控制器性能分析實驗表明,本文基于遞推雙線性子空間數據驅動建模的改進CFDL-MFAC 算法不僅可以精確跟蹤SNO,2和DO,5的目標值,而且能夠有效抑制外部擾動的影響,具有優良的控制性能和良好的魯棒性.