超聲蘭姆波檢測電路板缺陷的有限元仿真研究*

朱妍妍 陳 曉

（南京信息工程大學電子與信息工程學院 南京 210044）

1 引言

電路板的制造過程，包括元件的焊接以及電路板的組裝不可避免地會出現焊接缺陷或者質量上的缺陷，為了盡可能地找出電路板中的缺陷，電路板制造商正在加大對電路板的檢測、測試和分析。覆銅板是在印制電路板制造中的基板材料，在印制電路板中有著互連導通、絕緣和支撐的作用，并且電路中的信號傳輸速度、能量損失和特性阻抗等有很大的影響，所以電路板的各項性能在很大程度上取決于覆銅板。覆銅板具有一定厚度，可以看作一種薄金屬板，目前超聲檢測技術是國內外應用最廣泛的一種金屬板檢測技術，具有穿透力強，靈敏度高，成本低，響應速度快等優點［1～2］。由于蘭姆波是一種非平穩信號，具有多模式和頻散特性，傳播過程中遇到缺陷和端面會發生反射、散射以及模式轉換現象，多種模式信號疊加和頻散，使蘭姆波信號的分析變得十分復雜［3～4］。

有限元分析作為一種有效的數值分析方法［5］，利用仿真建模研究金屬板中蘭姆波的傳播特性，進而研究蘭姆波與缺陷之間的作用機理，為實際的缺陷檢測提供理論基礎。近年來許多學者利用有限元分析軟件在金屬板中激發單一模式蘭姆波［6］，研究了低頻模式下蘭姆波在金屬板中的傳播特性，并利用實驗驗證了相關結論。Roshan Joseph［7］提出了疲勞裂紋擴展的聲發射分析模型，利用有限元建模，在1mm厚鋁合金板上激發400kHz激勵信號，發現疲勞裂紋擴展過程中聲發射信號具有較強的S0蘭姆波模態。Yi Yang［8］利用三維有限元建模，在3mm 厚的鋁板上激發240kHz 的蘭姆波，研究了S0模式蘭姆波產生的二次諧波幅值與疲勞裂紋長度以及入射波角度之間的關系。王高平［9］利用有限元研究了健康鋁板和損傷鋁板中S0模態的傳播特性，實現了大小為12mm×8mm 的缺陷定位。陳澤宇［10］利用有限元模擬焊接模型，在2mm 厚鋼板上激發100kHz 對稱和反對稱蘭姆波，實現了裂紋的損傷定位和成像。顧建祖［11］利用數值仿真在1mm鋁板上激發150kHz 蘭姆波，驗證了利用導波成像算法對鋁板進行單損傷、雙損傷以及全域損傷成像。

以上學者的研究都是通過建立有限元模型，研究單一對稱S0模式在板中的傳播特性，并且進行了金屬板的損傷定位，但其頻厚積都低于1MHz·mm。具有一定的局限性。本文通過建立有限元模型，研究了無損鋼板在0～2MHz·mm 頻厚積下的頻散特性，隨后在鋼板上設置兩種不同缺陷，研究了蘭姆波在缺陷處的模式轉換現象，提出在頻厚積大于1MHz·mm 下反對稱A0模式比對稱S0模式蘭姆波對缺陷有更高的識別靈敏度，且A0模式對埋藏缺陷的靈敏度比表面缺陷高，為電路板的缺陷檢測提供理論基礎。

2 蘭姆波基本理論

2.1 蘭姆波的頻散特性

頻散是超聲蘭姆波的固有特性，當蘭姆波的激勵頻率發生變化時，其信號的傳播速度也會發生改變，因此檢測信號的波包會產生的時域展寬現象。實際檢測中通常設置窄帶脈沖信號來激勵蘭姆波特定模態，但一定帶寬中存在不同頻率成分，其信號頻散特性隨傳播距離的變化而變化，導致蘭姆波信號的包絡不斷發生變化，峰值也不斷減小［12～13］。

在超聲蘭姆波的理論研究中，相速度和群速度是兩個最基本的參數。相速度即相位變化速度，是波包上固定相位點在傳播方向上的速度。群速度是指脈沖波的包絡上具有某種特征點的傳播速度，也是波群能量的傳播速度［14］。蘭姆波的傳播速度不僅取決于板的密度、彈性和組織，還與板厚以及波的頻率特性有關。相速度cp和群速度cg可以表示為

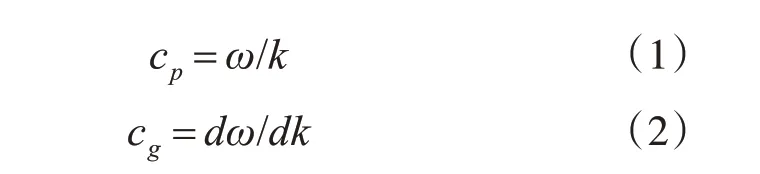
代入角頻率ω=2πf，波數k=ω/cp，群速度還可表示為

根據上述關系，繪制1mm 厚鋼板中蘭姆波的相速度和群速度頻散曲線如圖1所示。

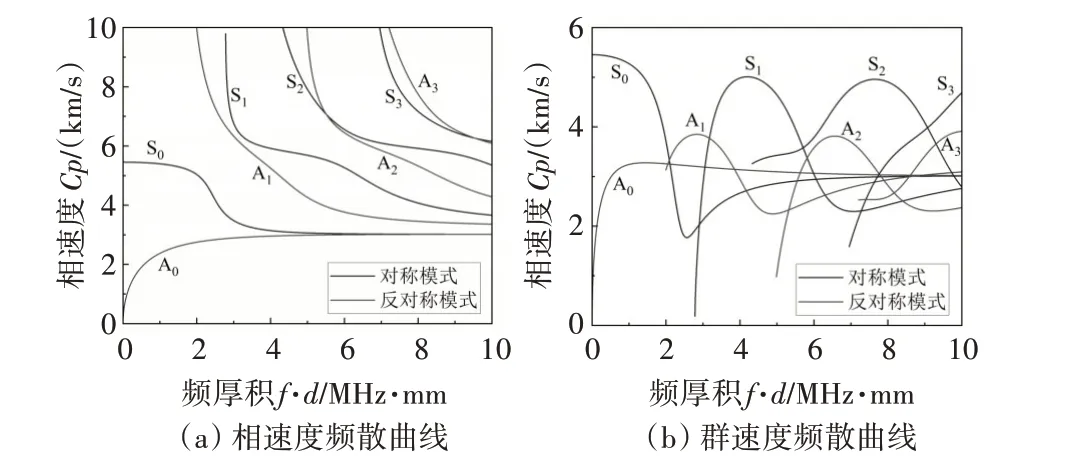
圖1 1mm厚鋼板中蘭姆波的頻散曲線

2.2 單模態蘭姆波

激發蘭姆波的方式有三種：單側激勵，對稱激勵和反對稱激勵，不同激勵方式如圖2 所示。使用單側激勵時，板中同時存在對稱模式和反對稱模式的蘭姆波。使用對稱激勵時，板中產生單一模態的對稱蘭姆波。使用反對稱激勵時，板中產生單一模態的反對稱蘭姆波［6］。

圖2 蘭姆波激勵方式

3 蘭姆波有限元仿真

3.1 鋼板有限元模型的建立

使用有限元軟件［15］建立鋼板有限元模型，研究不同激勵條件下蘭姆波信號的頻散特性。首先建立二維無損鋼板模型，如圖3 所示，尺寸為4mm×1000mm，材料屬性參數如下：密度ρ=7850kg/m3，彈性模量E=2×1011Pa，泊松比ν=0.3。

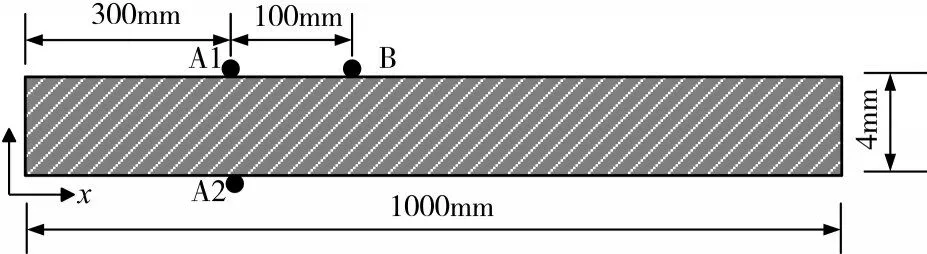
圖3 二維無損鋼板模型

在距鋼板左端300mm 處上下表面A1 和A2 分別進行單側激勵，對稱激勵和反對稱激勵，在距離激勵點100mm 處設置接收點B 采集響應信號。為了方便定位不同波包峰值的到達時間，激勵信號采用中心頻率為250kHz 的漢寧窗調制的3.5 周期正弦信號，模型網格劃分采用CPE4R 平面應變四邊形單元，網格尺寸為0.8mm，時間步長為0.01ms。建立動力顯式分析步，創建作業對模型進行求解。

3.2 仿真結果分析

3.2.1 不同激勵方式仿真結果

利用單側激勵對稱激勵和反對稱激勵方式的接收波形分別如圖4 所示。單側激勵由于同時存在S0和A0模式，兩種模式疊加較難區分，而對稱激勵和反對稱激勵只存在S0模式和A0模式，容易提取波峰到達時間計算其波包群速度。S0模式第一個直達波的波峰到達時間為26.3ms，激勵信號的波峰到達時間為7ms，通過計算可得S0模式波包的群速度為5181m/s，由頻散曲線可知當頻厚積為1MHz·mm時S0模式的理論群速度為5272m/s，相對誤差為1.7%，A0模式直達波的群速度為3154m/s，理論群速度為3244m/s，相對誤差為2.8%，因此之后的激勵方式采用對稱激勵和反對稱激勵進行研究。

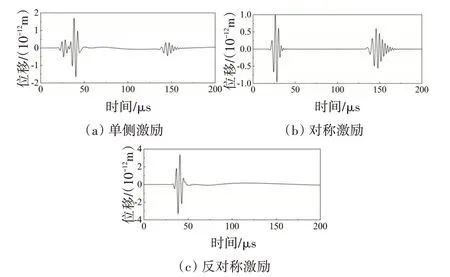
圖4 不同激勵方式接收波形

3.2.2 不同板厚下的群速度

為了研究不同板厚下的群速度頻散曲線，分別將板厚設置為1mm、2mm、3mm、4mm，依次設置激發頻率，使頻厚積在0～2MHz·mm 下，根據仿真測得的鋼板傳播10cm 處的波峰到達時間計算不同激發頻率下的群速度，和計算出來的理論群速度進行對比。仿真計算結果和理論計算結果如圖5 所示。從結果可以看出，蘭姆波傳播10cm 時的有限元仿真計算的S0模式群速度都比理論群速度小，A0模式群速度都比理論群速度大。

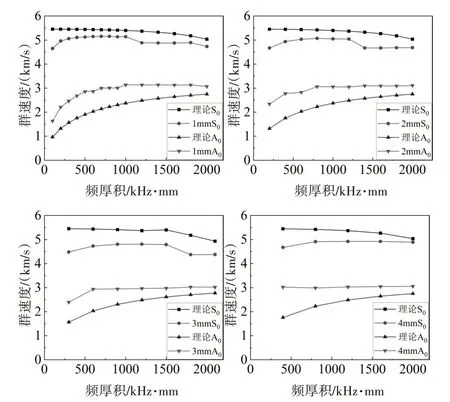
圖5 不同板厚下的群速度頻散曲線

3.2.3 不同傳播距離對頻散曲線的影響

上節頻散曲線是在傳播距離為10cm 時的測量結果，仿真結果與理論結果存在一定誤差，本節研究不同傳播距離對仿真測得的群速度是否有影響。本節選用2mm 厚度板，在傳播距離為2cm、4cm、6cm、8cm、10cm 處設置接收點，進行有限元仿真，利用得到的時域波形計算群速度，分析頻散曲線的變化情況。計算結果如圖6所示。

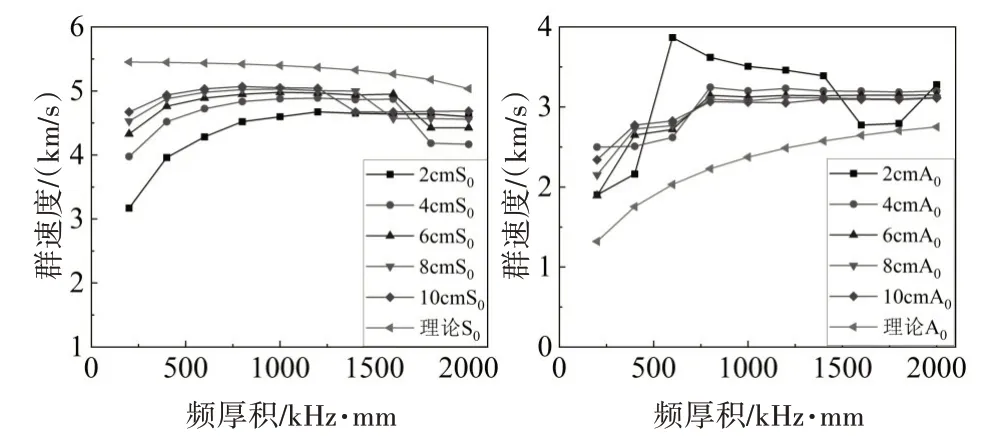
圖6 2mm板厚不同傳播距離測得的群速度頻散曲線

由仿真結果可知，蘭姆波在板中的傳播距離越短（2cm、4cm），仿真計算的群速度與理論群速度誤差越大，傳播距離增大時（6cm、8cm、10cm），仿真得到的群速度逐漸趨于一致。因此在有限元仿真時設置的接收點距激勵點的距離最好大于6cm，此時信號的變化趨勢更具有穩定性。

3.2.4 激發頻率對波峰幅值的影響

由于隨著頻厚積的變化，蘭姆波的頻散特性也是不斷變化的，頻散會導致波包在時域上展寬以及信號包絡峰值的減小，本節研究不同頻厚積下直達波波峰幅值的變化情況，傳播距離設置為10cm，仿真結果如圖7 所示，從結果可以發現在頻厚積小于1MHz·mm 情況下，S0模式的幅值都比A0模式的幅值大，當頻厚積大于1MHz·mm時，A0模式的幅值變大。從而也驗證了前人在頻厚積小于1MHz·mm時，采用S0模式進行蘭姆波傳播特性研究以及缺陷散射特性研究的合理性。

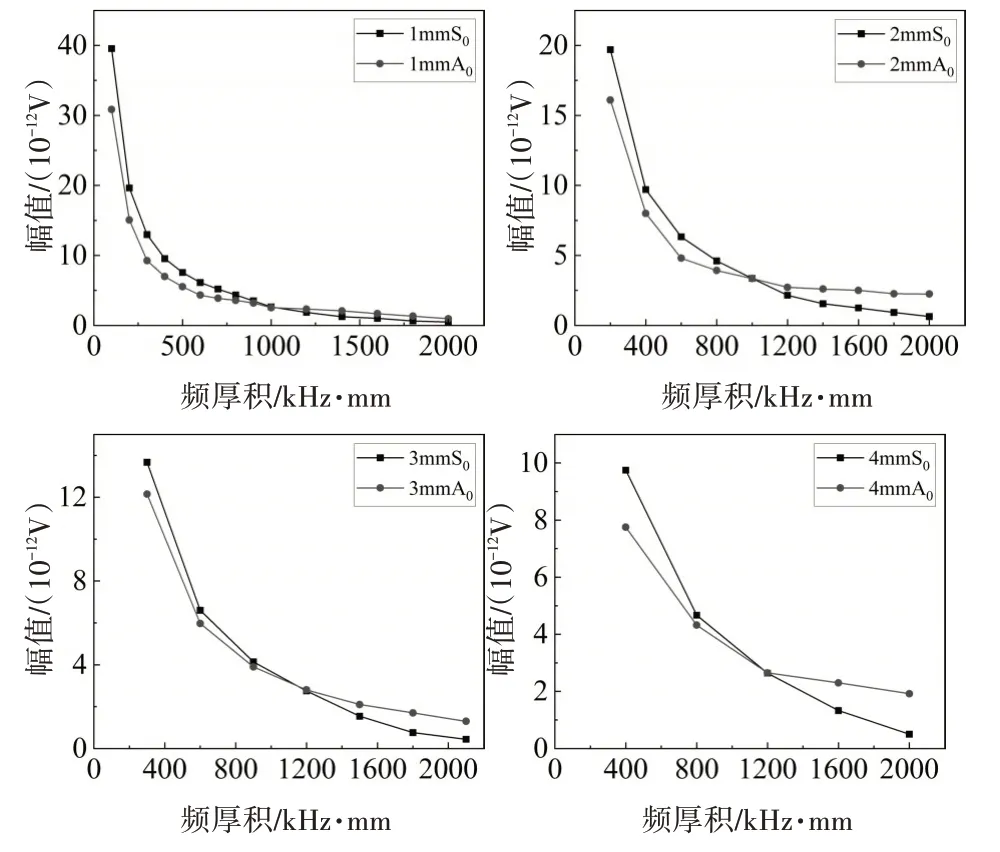
圖7 不同板厚下的波峰幅值變化曲線

3.3 缺陷鋼板的有限元仿真

在第3.1 節的基礎上，在距激勵點左端80mm處設置一個長1mm、寬0.5mm的表面缺陷和埋藏缺陷，埋藏缺陷深度位于板厚1mm 處（距上表面），缺陷示意圖如圖8 所示。首先利用有限元仿真模擬存在表面缺陷時，分析采用對稱激勵和反對稱激勵得到的結果，接收點采集到的時域波形如圖9 所示。

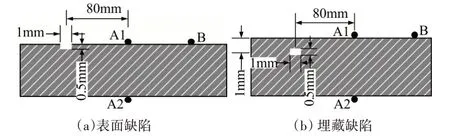
圖8 缺陷示意圖

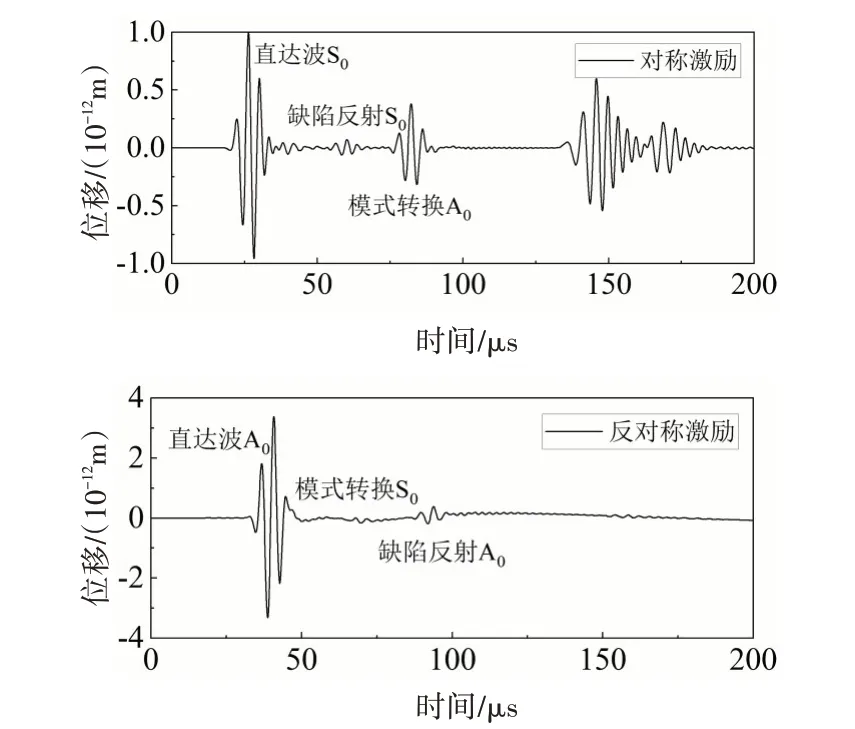
圖9 不同激勵方式下表面缺陷接收波形圖

對稱激勵接收波形圖中第一個波包和無缺陷接收波形相同，即S0模式的直達波信號，群速度為5181m/s，第二個波包波峰的到達時間為60.3μs，計算可得該波包的傳播距離為276mm，因此該波包是經缺陷反射的S0模式，理論傳播距離為260mm，誤差為6.1%。第三個波包波峰的到達時間為82.4μs，并不是S0模式經邊界反射的蘭姆波，根據蘭姆波缺陷傳播理論，無論是單一模式激勵還是多種模式激勵，當蘭姆波與缺陷發生交互作用后，模態轉換出的信號將同時包含入射頻率下的所有蘭姆波模式，在對稱S0模式傳播了80mm 后發生了模式轉換，部分信號轉換成了A0模式，經模式轉換后的S0和A0模式同時傳播180mm，根據不同模式的傳播速度，S0模式和A0模式波峰的到達時間相差22.3μs，實際到達時間相差22.1μs，誤差為0.9%，因此第三個波包為經缺陷模式轉換后的A0模式［16］。同理，反對稱激勵時第一個波包為A0模式的直達波信號，第二個波包為經缺陷發生模式轉換后的S0模式，第三個波包為經缺陷反射的A0模式。

對比經缺陷模式轉換后的S0和A0模式，無論是對稱激勵還是反對稱激勵，A0模式的波包幅度都比S0模式的波包幅度大，因此A0模式的轉換能量比S0模式的轉換能量大。結合圖7 所示波峰幅值的變化情況，在頻厚積大于1MHz·mm 時，反對稱模式A0比對稱模式S0更適合進行缺陷檢測。

利用有限元仿真研究不同缺陷類型下的反對稱A0模式蘭姆波反射波幅值的變化情況，仿真時域波形結果如圖10 所示，觀察可知A0模式對埋藏缺陷更敏感，因此利用有限元仿真研究反對稱A0模式與埋藏缺陷尺寸之間的關系。

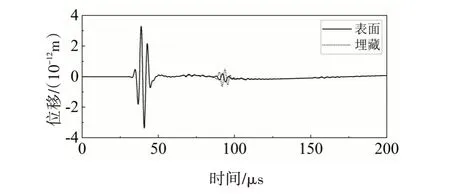
圖10 不同缺陷類型反對稱激勵接收波形

3.4 反對稱模式反射波與缺陷尺寸的關系

通過設置不同長度和寬度的埋藏缺陷來研究其與A0模式反射波之間的關系。設置缺陷寬度固定為0.5mm，長度分別為0.6mm、0.8mm、1mm、1.2mm、1.4mm、1.6mm，然后將缺陷長度固定為1mm，寬度分別為10mm、50mm、100mm、200mm、300mm、400mm、500mm，不同長度和寬度缺陷得到的仿真時域波形如圖11 所示，提取反射波波峰幅值以及功率譜峰值，繪制兩者與缺陷尺寸之間的關系，如圖12所示。

圖11 不同缺陷尺寸對應的時域波形圖

圖12 不同缺陷尺寸下A0模式反射波波峰以及功率譜峰值

從圖11 仿真結果可以看出，不同缺陷尺寸大小對A0模式的直達波幅值影響不大，主要影響的是缺陷反射波的幅值，擬合波峰幅值以及功率譜峰值與缺陷長度和寬度之間的關系如圖12 所示，反射波波峰與功率譜峰值與缺陷長度之間的關系可以進行線性擬合，反射波波峰與功率譜峰值與缺陷寬度之間的關系可以進行三次方擬合。通過建立波峰和功率譜峰值與缺陷尺寸的關系，在缺陷尺寸未知的情況下，通過時域波形的包絡以及頻譜分析可以推測缺陷的長度和寬度，為電路板的缺陷檢測提供參考。

4 結語

為了檢測覆銅電路板中的缺陷，本文利用金屬板中蘭姆波頻散方程，繪制了1mm 厚鋼板的蘭姆波理論頻散曲線，利用有限元軟件建立鋼板有限元模型，通過仿真結果研究鋼板中的不同模式的在缺陷處的傳播特性，得到如下結論：利用有限元仿真計算得到的對稱蘭姆波S0模式的群速度都比理論群速度小，反對稱A0模式群速度都比理論群速度大。接收點距激勵點的距離越短（2cm、4cm），仿真計算的群速度與理論群速度誤差越大，傳播距離增大時（6cm、8cm、10cm），仿真得到的群速度逐漸趨于一致；在0～1MHz·mm頻厚積下，對稱S0模式的峰值都比反對稱A0模式的峰值大，當頻厚積大于1MHz·mm 時，A0模式的峰值變得比S0模式大；無論是對稱激勵還是反對稱激勵，遇到缺陷模式轉換的A0模式都比S0模式能量大，在頻厚積大于1MHz·mm 時，反對稱A0模式比對稱S0模式更適合進行無損檢測；對于同樣大小的表面缺陷和埋藏缺陷，反對稱A0模式對埋藏缺陷更敏感，A0模式的反射波波峰與功率譜峰值與缺陷長度之間的關系可以進行線性擬合，與缺陷寬度之間的關系可以進行三次方擬合。未來可以結合其他智能算法［17～26］進一步提高缺陷檢測的精度。