基于貝葉斯優化的LSTM高速交通流量預測

沈 括，朱怡帆，孟祥毅，李海濟

（安徽大學互聯網學院，合肥 230031）

0 引言

由于城市可利用土地不斷減少，而機動車流量持續增加，城市的交通系統建設速度無法滿足日益增長的交通需求，交通擁堵的情況日益常態化。百度地圖公布數據顯示，2020 年中國交通擁堵排名前三的城市分別是重慶、貴陽和北京，長期的交通擁堵不僅增大了交通管理難度，還容易發生交通事故。如何緩解交通擁堵、提高通行效率是如今智慧交通面臨的重要課題。

在現如今的大數據時代背景下，交通數據的規模不斷增大，累積的數據顛覆了傳統數據的規模，甚至可以達到PB 級別。基于傳統統計模型的數學方法已很難處理這些海量數據，而利用大數據平臺所提供的強存儲和強計算能力，結合一些神經網絡模型、機器學習算法等，可以較好地對大規模交通流量進行預測。

早期的交通流量預測模型，如整合移動平均自回歸法（ARIMA）、支持向量機（SVM）、馬爾科夫鏈模型（Markov chain model）等，雖然取得了不錯的預測效果，但無法深入挖掘數據之間的內在聯系。長短期記憶神經網絡LSTM 可以挖掘大數據之間的深層關系，而且能滿足神經網絡需要大量數據訓練的特征，因此該模型在交通、電力等領域的預測中應用廣泛，并呈現出良好的長期與短期預測性能。

目前，國內外很多學者對LSTM 模型及應用領域都開展了廣泛的研究。瑞典首都斯德哥爾摩、東京、紐約等一些國際性大都市，近些年來也一直致力于交通信息系統解決交通擁堵問題。Altché 和Fortelle在第20 屆智能運輸系統國際會議上提出利用LSTM 模型預測車輛行駛軌跡。Santosh 等使用大數據技術結合LSTM 模型預測瘧疾發病率。國內，程肇蘭等基于LSTM研究鐵路貨運量預測。本文在LSTM 基本模型基礎上，構建了基于貝葉斯優化的LSTM 模型，探究交通流量預測，并驗證模型的有效性與準確性。

1 基礎理論簡介

1.1 LSTM神經網絡

LSTM是一種在RNN的基礎上提出的特殊循環神經網絡。相較于傳統的循環神經網絡，LSTM 可以很好地解決梯度消失和梯度爆炸的問題。其核心之處在于設計一個記憶細胞，具備選擇記憶的功能，可以選擇記憶重要信息，過濾掉噪聲信息，減輕記憶負擔。LSTM 使用遺忘門、輸入門、輸出門來控制信息，完成該網絡功能的實現。圖1給出了LSTM的工作原理。

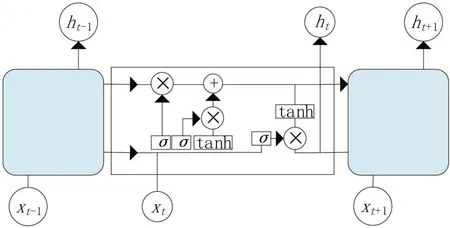
圖1 LSTM工作原理

（1）遺忘門。遺忘門的作用是選擇性保留細胞中的信息并舍棄價值低的信息，其計算公式為：

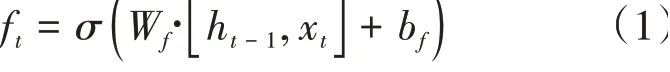
W為遺忘門的權重矩陣，h為上一時刻輸出向量，x為當前輸入向量，b為偏置項，為激活函數。

（2）輸入門。輸入門的作用是將重要的信息選擇性地記錄到細胞中，根據細胞狀態決定當前時刻的輸入，其計算公式為：

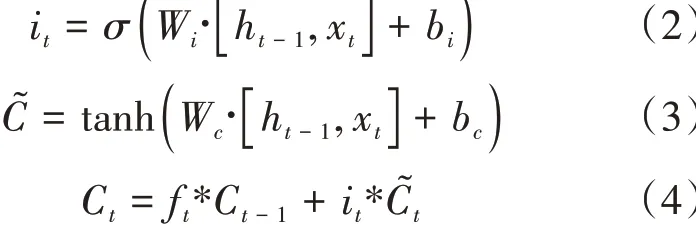
W為輸入門的權重矩陣，x為當前輸入向量，h為上一個時刻輸出向量，b、b為偏置項，、tanh為激活函數，f為遺忘門的輸出，i是要保留下來的新信息，?是新數據形成的控制參數，最終實現狀態的更新。

（3）輸出門。輸出門的作用是基于細胞狀態決定最終輸出結果。其計算公式為：

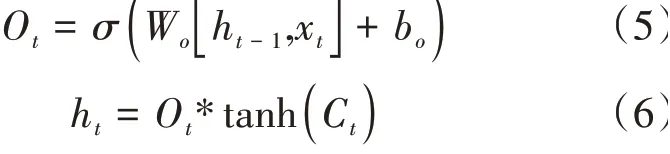
W為輸出門的權重矩陣，b為偏置項，最終得到h可以作為LSTM 的輸出值和下一個狀態的輸入值。

1.2 貝葉斯優化算法

普通求函數極值的問題，可以利用基于梯度的優化來解決。但在LSTM 模型調參的過程中，不能夠直接確定對應的函數關系，所以無法使用傳統的優化算法來對超參數進行調優。而貝葉斯優化算法是一種black box 優化算法，不需要知道目標函數的表達式，以極其簡潔的框架來尋找全局最優解，非常適用于LSTM 模型的調參。

算法的思路是利用目標函數的先驗概率分布及已知觀測點來更新后驗概率分布，然后根據后驗概率分布尋找下一個極小值點，使極小值不斷減小，最終得到最優超參數。定義貝葉斯優化目標為：

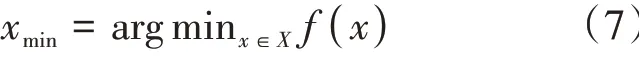
式中是最終優化的超參數，( )是待優化的目標函數。

式中Σ(,)是協方差矩陣：

由貝葉斯定理可知：

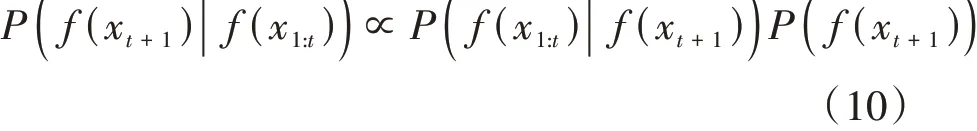
通過不斷的迭代更新使= x,最終得到最優化的超參數。

算法流程如下：

表示模型未知的目標函數，即所謂的black box；表示所要優化超參數的搜索空間；表示數據集；表示采集函數；表示高斯模型。

1.3 評價指標

本文采用均方根誤差和平均絕對誤差指標來對不同模型的預測結果進行評估。

（1）均方根誤差（RMSE）

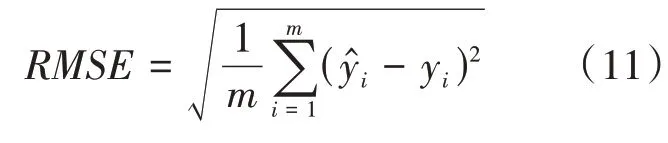
均方根誤差指預測值與實際值偏差平方的平均值再取平方根，用來衡量預測值和實際值之間的偏差。

（2）平均絕對誤差（MAE）

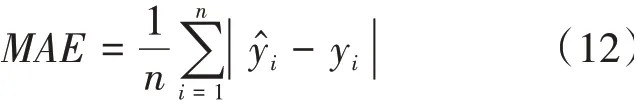
平均絕對誤差指各次預測值與實際值的絕對偏差的平均值，可以避免誤差相互抵消的情況。

2 基于貝葉斯優化的LSTM模型

在傳統的LSTM 神經網絡訓練過程中，需要人為調節超參數。超參數的取值對模型的性能有很大的影響，但超參數的選擇無規律性，且具有很大的偶然性，這對人為調參很不友好，往往無法得到最優超參數。針對這一問題，本文引入貝葉斯優化算法，貝葉斯優化算法主要包含概率代理模型和采集函數兩個部分。概率代理模型可以利用高斯過程尋找目標函數的近似，得到目標函數的后驗概率分布；采集函數根據后驗概率分布，在未知區域和已觀測到出現最優結果的區域進行采樣，選擇合適的樣本點使得目標函數取極值。綜上分析，本文引入基于貝葉斯優化的LSTM模型。

該模型分為三個階段，第一階段訓練LSTM模型，第二階段將需要進行優化的超參數傳入貝葉斯優化模型，第三階段利用優化后的LSTM模型輸出預測結果。圖2給出了基于貝葉斯優化的LSTM模型流程。

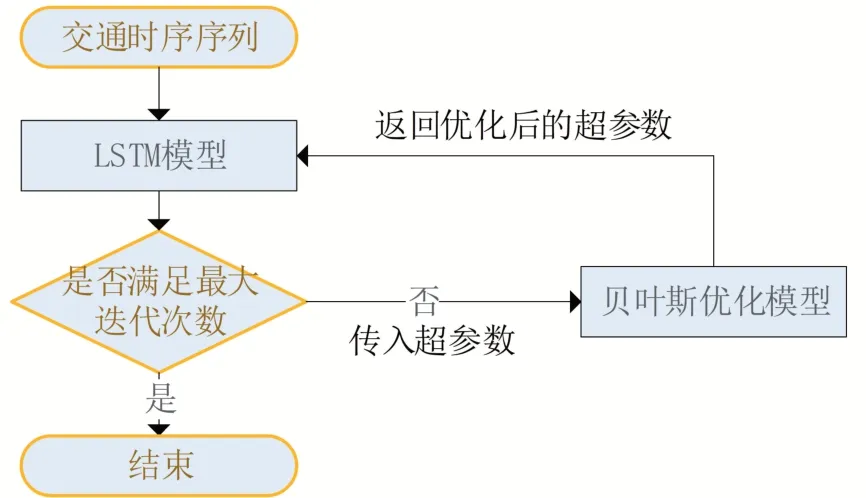
圖2 基于貝葉斯優化的LSTM模型流程

（1）LSTM訓練階段

步驟1 超參數初始化。

步驟2 輸入訓練集進行LSTM 神經網絡的訓練。

步驟3 輸出與訓練集維度一致的數據，并不斷地對超參數進行更新。

（2）貝葉斯優化階段

步驟1 定義需要優化的超參數，并設置參數空間。

步驟2 定義優化目標函數，并將定義的超參數帶入LSTM模型進行訓練。

步驟3 利用高斯過程求目標函數的后驗概率分布，根據后驗概率分布對超

參數樣本點進行采樣，優先選擇最優超參數，實現對超參數的更新。

步驟4 不斷更新目標函數的后驗概率分布和超參數，直至滿足模型的要求。

（3）LSTM預測階段

步驟1 將驗證集傳入訓練好的LSTM模型，輸出預測結果。

步驟2 根據預測結果求出誤差。

3 實例分析

3.1 數據來源

本文使用的數據集是2018 年英國高速公路數據集，該數據集以十五分鐘為周期，連續觀測高速公路的流量。其基本信息如表1所示。

表1 數據集的基本特征

3.2 數據的預處理

（1）原數據集主要包含時間、不同種類車流量和速度等信息，但存在某些缺失值和異常值，需要對數據集進行清洗，去除缺失值和異常值。

（2）根據原數據集的不同種類的車流量計算某一時刻的總車流量。

（3）對數據進行歸一化處理（按最大最小值中心化，再按極差縮放），去除量綱影響。

（4）將前90%的數據集作為訓練集，后10%的數據集作為驗證集。

3.3 模型對比

本文使用keras 框架來進行神經網絡模型的訓練，引入序貫模型來描述各層網絡。為了進一步探究貝葉斯優化的LSTM 模型處理時序序列的優越性，本文建立了RNN 神經網絡模型、GRU神經網絡模型與其進行對比。

3.3.1 RNN神經網絡模型

RNN 是指隨時間推移重復發生的結構，一般適用于處理序列數據。RNN 記憶模塊可以獲取計算過的信息，具體表現為對上一時刻的信息進行記憶并應用到當前時刻的輸出。其最大的特點是循環利用不同時刻的信息，但隱含層的輸入會隨著時間的推移覆蓋原有信息，造成梯度消失問題。

3.3.2 GRU神經網絡模型

與LSTM相似，GRU的設計也是為了解決長期記憶依賴中的梯度消失和梯度爆炸等問題。相較于LSTM復雜的重復網絡模塊，GRU只有更新門與重置門，結構大大簡化的同時也保持了較好的效果。更新門的作用是決定更新的效果，控制上一時刻的特定信息保存到當前時刻，重置門的作用是控制上一時刻的特定信息被忽略。通過兩個門函數，GRU 最終將重要信息保存下來。

4 實驗結果與分析

4.1 實驗結果

圖3給出了不同模型在驗證集上的預測效果，表2 給出了不同模型預測結果的誤差指標，可以看出貝葉斯優化的LSTM 模型預測的結果最優。

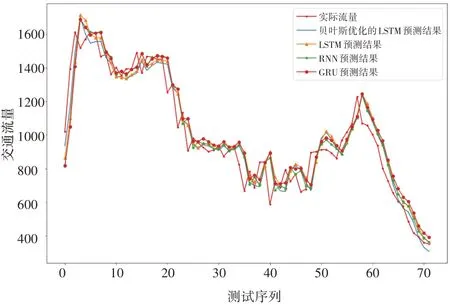
圖3 各模型流量預測結果

根據表2 的結果可知，貝葉斯優化的LSTM模型預測結果的RMSE、MAE 分別為95.683、75.373。相較于LSTM 模型，均方根誤差降低了6.30%，平均絕對誤差降低了5.67%；相較于RNN 模型，均方根誤差降低了10.10%，平均絕對誤差降低了7.44%；相較于GRU 模型，均方根誤差降低了16.12%，平均絕對誤差降低了13.20%。可以看出貝葉斯優化的LSTM模型預測結果更接近真實值，精度更高。

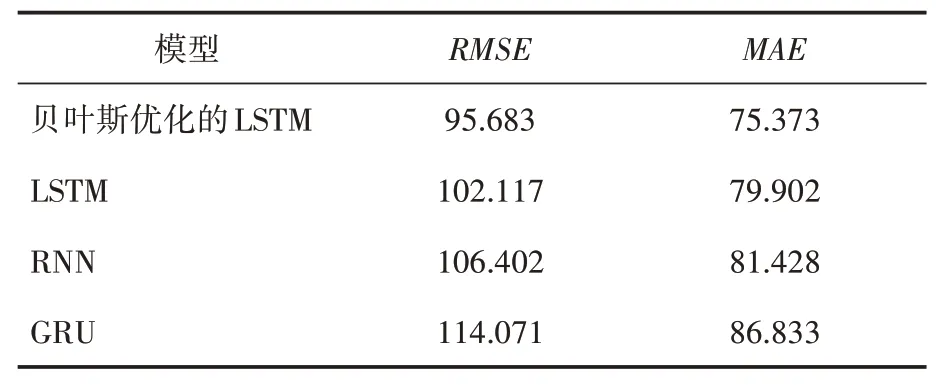
表2 對高速公路時間序列預測結果

4.2 誤差分析圖

圖4給出了不同模型的誤差對比柱狀圖，圖中的柱狀圖越高則說明誤差越大。從圖4可以看出，GRU 模型的RMSE 和MAE 對應的柱狀圖最高，貝葉斯優化的LSTM 模型的RMSE 和MAE對應的柱狀圖最低，說明貝葉斯優化的LSTM 模型誤差最小，相較于其他模型優勢明顯。

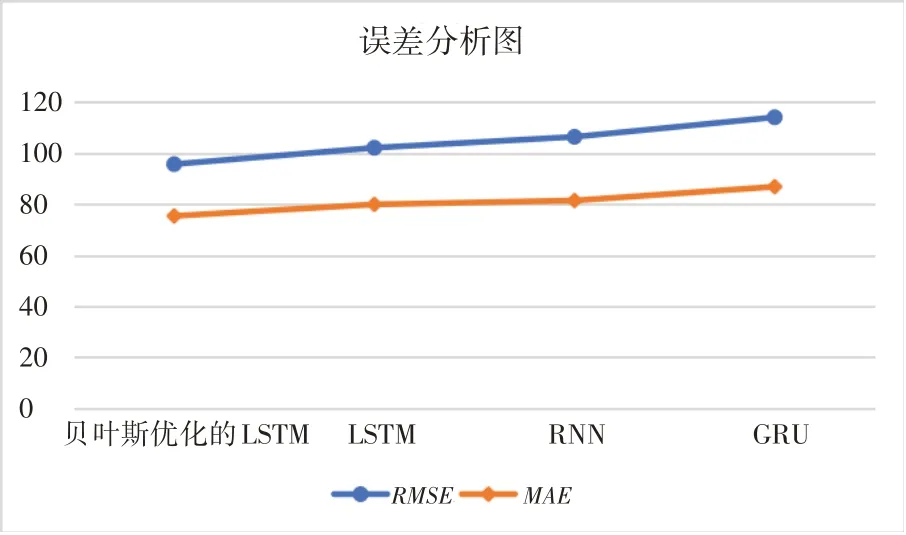
圖4 不同模型的誤差分析

5 結語

本文提出了基于貝葉斯優化的LSTM 模型，用于探究高速交通流量預測問題。首先對模型的基本理論進行了分析，然后引入貝葉斯優化的LSTM 模型，最后進行實例分析來驗證模型的優越性。通過實驗結果可以看出，基于貝葉斯優化的LSTM 模型預測精度高于其它模型，能夠準確地預測高速交通流量，具有一定的應用價值。在高速交通流量預測過程中，影響因素復雜多變，探究多因素模型對預測精度的影響將是下一步的研究方向。