一種空間匹配的高速飛行目標軌跡估計方法

鄧 步，李弘毅，顧亞平

（1.中國科學院聲學研究所東海研究站，上海 201815；2.中國科學院大學，北京 100049）

0 引言

相對于光學和雷達目標探測，低空目標聲探測采用被動探測方法，受環境影響較小，因此受到廣泛關注[1-3]。當目標離測點陣列的距離較近時，可將傳感器陣列所獲得的信號視為滿足球面波，此時可將測得的信號到各個陣元的時間差作為先驗信息 進行參數估計，得到運動參數[4]或定位參數[5-6]。當目標離測點陣列的距離較遠時，聲信號視為平面波，進而測得信源方位[7]，再利用陣列網絡進行定位[8]。

文獻[9]提出了一種基于聲多徑傳播模型的目標運動參數估計方法。該方法利用不同路徑聲信號的到達時間估計值，實現對目標運動參數的估計，該方法要求布設盡可能多的長基線聲傳感器陣。

文獻[10]對瞬時頻率方法進行了拓展，提出了一種基于單聲傳感器陣列的目標運動軌跡估計方法。該方法首先利用多普勒效應估計目標飛行參數，結合波達方向（Direction of Arrival,DOA）估計目標軌跡方向、水平偏置和高度，依據幾何模型確定其運動軌跡。該方法主要適用低速飛行目標。

文獻[11]提出了基于五元十字陣的低空目標聲測無源定位算法。在時延估計方面，該文獻提出了基于維納加權的頻域自適應時延估計算法和基于雙譜的時延估計算法。在小尺寸高精度定向方面，該文獻首次將壓差式矢量聲傳感器引入低空目標側向研究中，提出基于矢量傳感器陣的寬帶相干信號子空間最優波束形成算法。

文獻[12]利用布設于有限空間內的聲傳感器陣實現低空高速目標跟蹤為背景，通過對某典型低空高速目標噪聲波形的分析，發現其噪聲呈現寬帶低頻譜特征。因此，該文獻主要研究了基于時延估計的目標定位跟蹤方法，提出了多面交匯的目標軌跡估計方法。

目前對低空飛行目標的研究主要集中在直升機、無人機等低速目標，而低空高速飛行目標威脅性更高，且更加難以跟蹤。高速飛行目標的噪聲是一類瞬態信號[10]，難以準確獲取其信號特征，給定位跟蹤帶來了較大困難。

影響高速目標軌跡測量精度的原因很多，但主要因素有：（1）目標高速運動，會產生多普勒頻移；（2）環境中的風速是時變的，且風向具有不確定性，造成聲音傳播各向異性。兩者均會引起陣列中陣元的測量誤差。

因此，在對高速飛行目標進行波達方位估計時，不可避免地存在估計誤差。同時，當目標高速運動的速度接近聲速時，在某一時刻上，不同陣列所接收到的信號并非信源在同一時刻所發出，難以在時間維度上進行對齊。針對上述問題，借鑒點云數據處理的思想[13]，本文在探測范圍內建立字典，提出了一種基于空間匹配的軌跡估計方法。仿真結果表明，在一定誤差范圍內，軌跡估計結果依然表現良好，達到預期目的。

1 字典建立

假設目標的探測范圍已知，即目標出現在100 m×100 m×200 m 的空間范圍內，在探測區域頂點處安裝相同的測向陣列，如圖1 所示。目標從任意方向飛過探測區域時，至少從兩個陣列之間穿過。將陣列1 位置視為坐標原點。每個陣列從字典建立到平面擬合流程一致，本文以陣列1 進行推導說明。

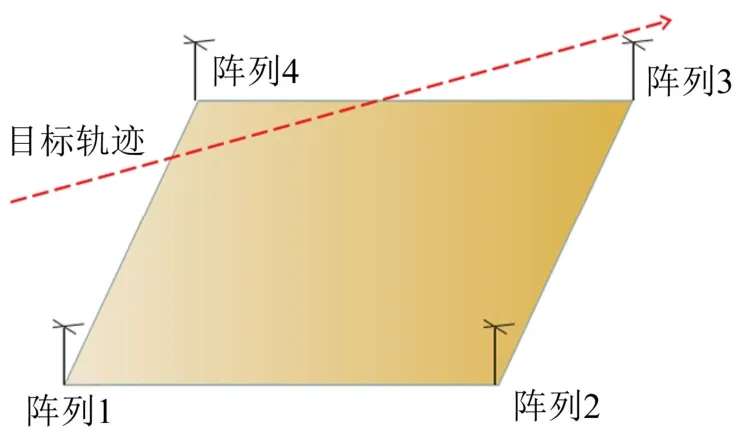
圖1 目標探測區域示意圖 Fig.1 Schematic diagram of target detection area

將空間內水平和垂直距離以設定間距d1為間隔進行劃分，即若d1=1 m，該空間被劃分為2×106個具有獨立坐標的確定的空間點，表示為：（xi,yi,zi）,i=1,2,…,N。空間點示意圖如圖2 所示。

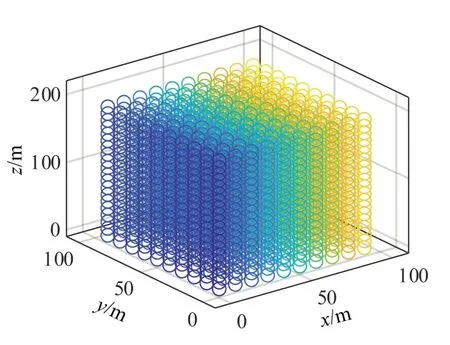
圖2 空間點示意圖 Fig.2 Space point diagram

每個點相對于位于原點的陣列1 的方位角與俯仰角可通過坐標轉換公式進行轉換，投影到極坐標下。將N個空間點的方位角θ與俯仰角?構成字典進行數據存儲。即：

2 軌跡估計

將接收到的信號進行分幀處理，計算每一幀數的波達方位，設有K幀數據，結果表示為

計算每幀數據得到的波達方向與字典中每個空間點方位角與俯仰角的均方誤差，表示為

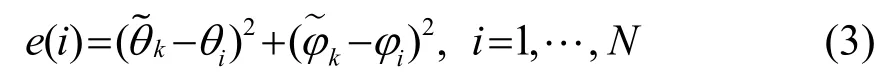
單幀數據計算得到的波達方位與空間點字典產生N個誤差結果。再進行最小誤差匹配，即將計算得到的誤差進行排序，搜索誤差最小的n個點進行存儲，表示為

當n=100 時，最小誤差分布圖如圖3 所示。從圖3 中可以看到，匹配得到的n個誤差最小空間點在空間中沿著一定方向進行分布且分布密度與空間點和陣列1 的幾何距離成正比。

圖3 最小誤差分布圖 Fig.3 Schematic diagram of the minimum error distribution

2.1 三維空間直線擬合

本文使用整體最小二乘法[14-15]，對單幀數據得到的n個誤差最小空間點進行擬合，以獲得空間直線的幾何參數，為后續平面擬合做準備。

將空間直線的點向式方程變形為

式中：x0、y0、z0為空間直線的已知點；A、B、C為待求參數。

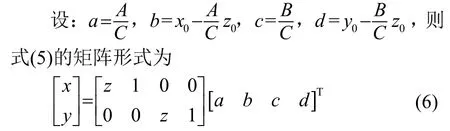
設V為擬合誤差，I為單位矩陣，對存儲的n個誤差最小空間點進行構造誤差方程。根據最小二乘理論中的間接平差模型[16]，令：

則誤差方程表示為

整體最小二乘法是同時顧及觀測值和系數矩陣誤差的一種平差方法，相比于最小二乘法，其參數估值是統計最優解。本文采用易于編程實現的整體最小二乘迭代法，解算式（8）中的空間直線的誤差方程，平差準則為

代入式（8），對系數矩陣B和參數向量X中各元素進行求導，獲得迭代方程式：

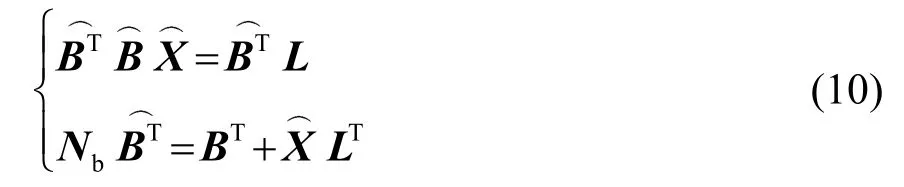
其中：

設初始值為X0，使用整體最小二乘迭代法對誤差最小的n個點進行擬合，結果如圖4 所示。

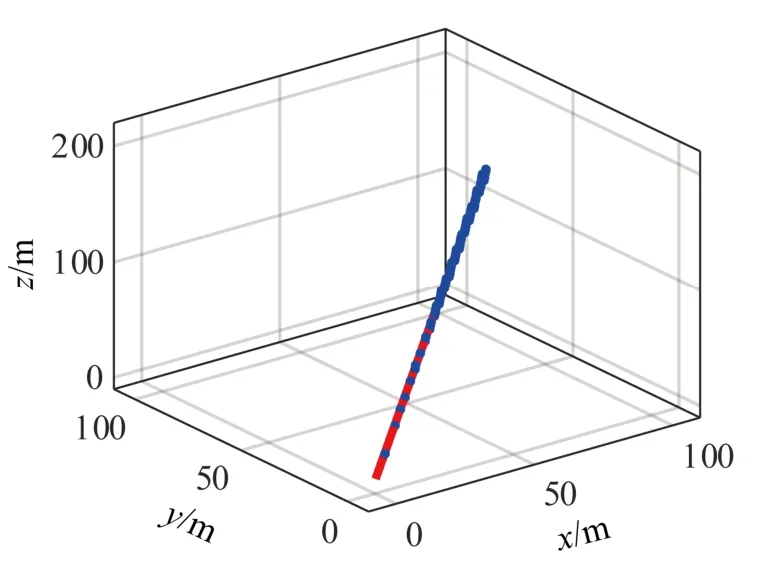
圖4 整體最小二乘直線擬合結果 Fig.4 The result of overall least squares linear fitting

該直線的方向向量可視為目標與陣列坐標的矢量方向，即可視為真實目標位置估計點位于該擬合直線上。

同理對K幀數據連續進行上述處理，擬合結果如圖5 所示。

圖5 對K 幀數據進行的整體最小二乘直線擬合結果 Fig.5 The result of overall least square linear fitting for the K-frames of data

2.2 穩健最小二乘平面擬合

由于高速飛行目標在探測范圍內為直線運動，在一個陣列的條件下，多幀最小二乘擬合直線理想情況下共面，即均在同一個平面上。理想條件下，兩條共面直線即可確定平面，但在2.1 節中對直線進行擬合時存在一定誤差，因此直線共面條件不可能實現。此時使用空間直線上的采樣點來對平面進行擬合，得到由方向直線構成的近似平面。本文在每幀數據所確定的直線上均勻采樣100 個點構成空間點數據集M，該數據集中不存在異常點，受文獻[13,17-18]啟發，采用一種穩健最小二乘平面擬合方法。理論上，兩幀數據所構成的空間點數據集即可確定相應平面。

使用多項式函數表示平面：

式中：u、v、w為待求參數。

設數據集：

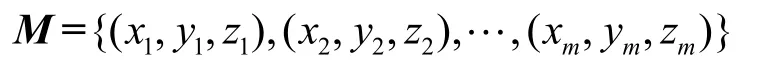
其最佳擬合平面應滿足：

由式（12），式（13）可以表示為

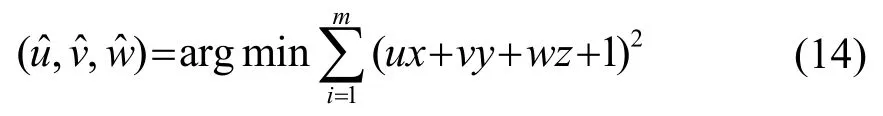
對式（14）中的u、v、w求偏導使其為0。整理后設：

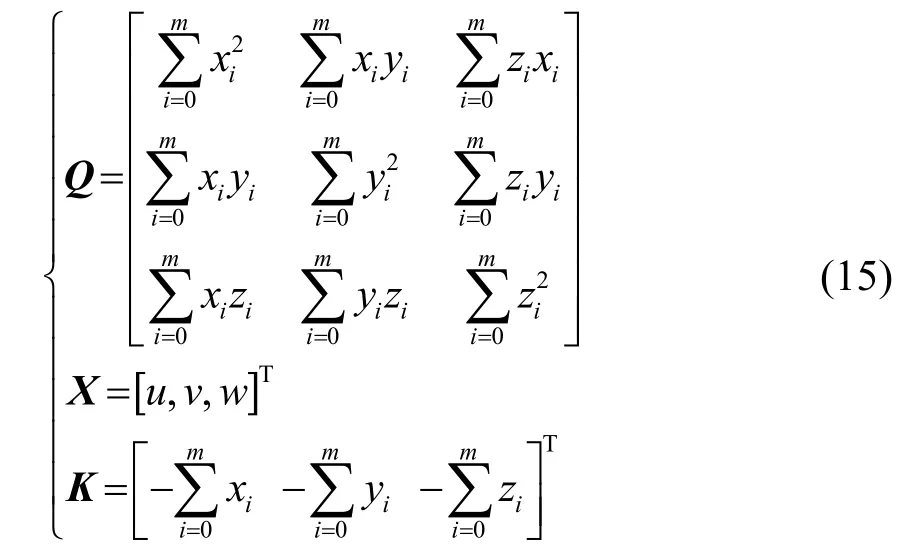
則可得：

可解得平面方程系數為

設Di為數據集M中點到擬合平面的距離，為數據集M中點到擬合平面的平均距離。精度評定距離標準偏差為

利用式（17）求得的u、v、w對平面特征向量進行初始化，計算出數據集M中每個點至擬合平面的距離Di。當Di≥ 2σ時，此點被認為是異常點并刪除；反之,則保留。再利用所有保留下來的點通過式（13）—式（18）重新計算進行迭代，直到剩下所有點的Di都在規定的閾值之內，即Di都小于標準偏差的2 倍時為止，獲得最佳的u、v、w構造平面特征向量，進而獲得擬合平面。

對2.1 節中所得擬合直線進行平面擬合，結果如圖6 所示。

圖6 擬合直線的平面擬合 Fig.6 Plane fitting by fitted lines

2.3 軌跡估計

由圖1 可知，目標從任意方向進入探測區域時，始終位于至少兩個陣列的中間區域。高速飛行目標在探測區域內可以視為直線運動，而空間中兩個不平行平面即可確定一條相交直線，即為估計得到的目標運動軌跡，算法流程圖如圖7 所示。

圖7 估計目標飛行軌跡的算法流程圖 Fig.7 Algorithm flowchart for target flying trajectory estimation

設陣列1 位于坐標點（0,0,0），陣列3 位于坐標點（0,100,0），對于單個陣列，分別使用兩幀數據與多幀數據進行軌跡估計，目標軌跡估計與顯示如圖8、9 所示。

如圖8（a）、8（b）所示，兩平面交線即為估計軌跡。如圖9（a）、9（b）所示，紅色點為真實軌跡點，綠色點為本文算法估計得到的軌跡點。仿真結果驗證了兩個陣列分別僅使用兩幀數據即可估計出目標軌跡。可以通過增加使用的數據幀數提高估計精度，該方法可較為準確地對目標進行軌跡估計。

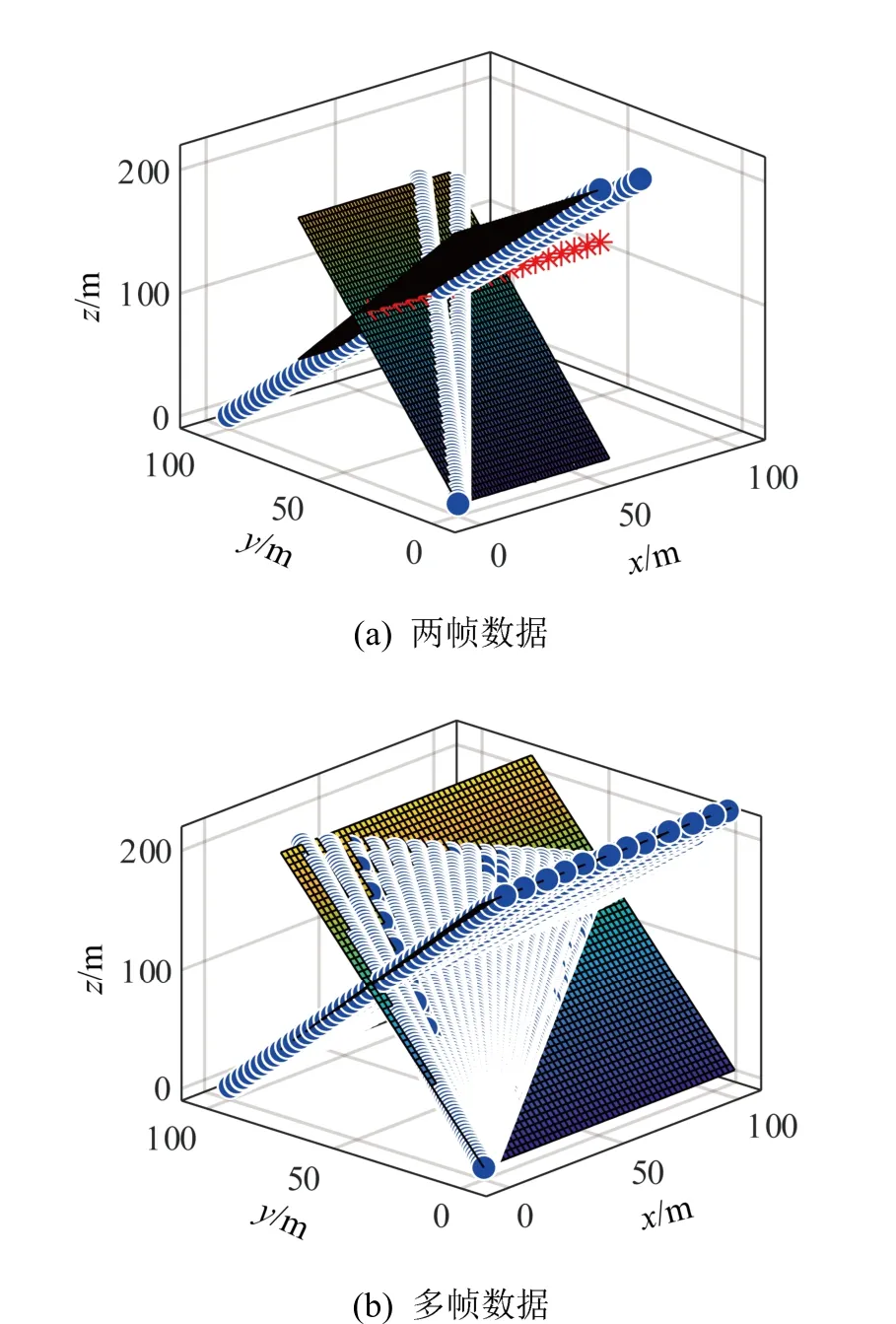
圖8 不同幀數據的軌跡估計結果 Fig.8 Trajectory estimation results by different frames of data

圖9 真實軌跡與估計軌跡 Fig.9 Real trajectory and the estimated trajectory

3 誤差分析

3.1 軌跡誤差

高速飛行目標在探測范圍內為直線運動，軌跡估計結果也為空間中的直線方程。由于探測范圍已知，設在x軸上[0,100]范圍內，同樣以d1為間隔，對估計的軌跡ME與真實軌跡MT進行采樣，數據點數為n，分別表示為

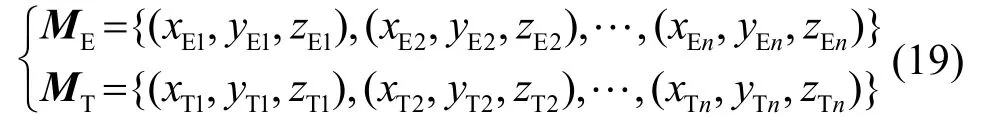
軌跡估計誤差表示為

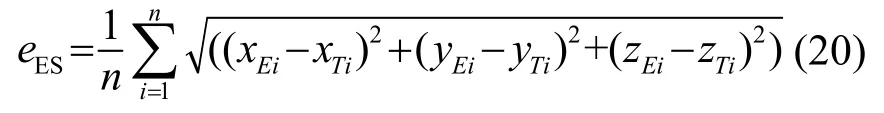
3.2 數據幀數對誤差的影響

由于直線擬合與空間擬合均存在誤差，估計得出的軌跡誤差與數據幀數有直接關系，如表1 所示。

表1 數據幀數對軌跡估計誤差影響 Table 1 The influence of the number of data frames on the trajectory estimation error

3.3 單陣列安裝誤差對軌跡估計結果影響

由2.3 節可知，使用兩個陣列（陣列1、陣列2）即可估計出目標軌跡。若忽略陣列1 誤差，陣列2 由于陣列設備安裝產生方位估計誤差。設陣列2 對每幀數據進行方位估計誤差相同，俯仰角與方位角誤差范圍均為[? 3°,3°]，誤差分辨率為0.1°。目標飛行高度分別為60.9、90.9、120.9 m，誤差結果如圖10 所示。

圖10 單陣列波達方位估計誤差對軌跡估計誤差的影響 Fig.10 Influence of DOA estimation error of a single array on trajectory estimation error

3.4 雙陣列安裝誤差對軌跡估計結果影響

若考慮陣列1、2 由于陣列設備安裝產生的方位估計誤差。設陣列1、2 對每幀數據進行方位估計誤差相同，俯仰角與方位角誤差范圍均為[? 3°,3°]，誤差仿真步長為0.1°。目標飛行高度分別為60.9、90.9、120.9 m，誤差結果如圖11 所示。

圖11 雙陣列波達方位估計誤差對軌跡估計誤差的影響 Fig.11 The influence of double-array DOA estimation error on trajectory estimation error

3.5 雙陣列隨機誤差對軌跡估計結果影響

同時考慮陣列1、2 產生的波達方位估計誤差對軌跡估計造成的影響。設陣列1、2 對每幀數據進行波達方位估計誤差為隨機誤差，設俯仰角、方位角隨 機誤差 范圍均 為[? 5 °,5 °]、[? 7 °,7 °]、[? 9 °,9 °]，誤差仿真步長為0.1°，進行蒙特卡洛仿真。軌跡估計誤差數值分布與軌跡估計誤差統計分布如圖12～14 所示，軌跡估計平均誤差與最大誤 差如表2 所示。

圖12 波達方位估計隨機誤差在[-5°,5°]對軌跡估計影響 Fig.12 Influence of the random error of DOA estimation on the trajectory estimation in [-5°,5°]

圖13 波達方位估計隨機誤差在[-7°,7°]對軌跡估計影響 Fig.13 Influence of the random error of DOA estimation on the trajectory estimation in [-7°,7°]

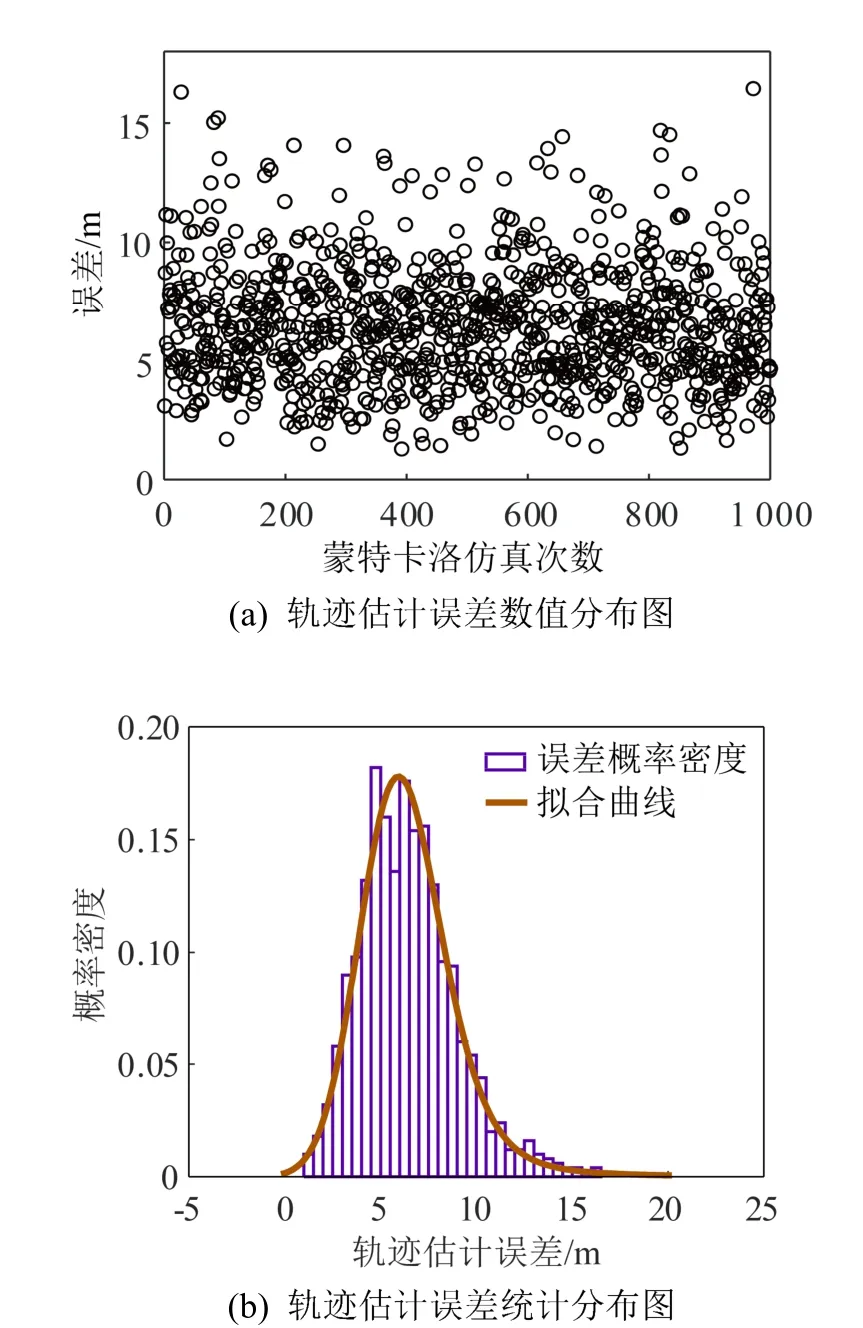
圖14 波達方位估計隨機誤差在[-9°,9°]對軌跡估計影響 Fig.14 Influence of the random error of DOA estimation on the trajectory estimation in [-9°,9°]

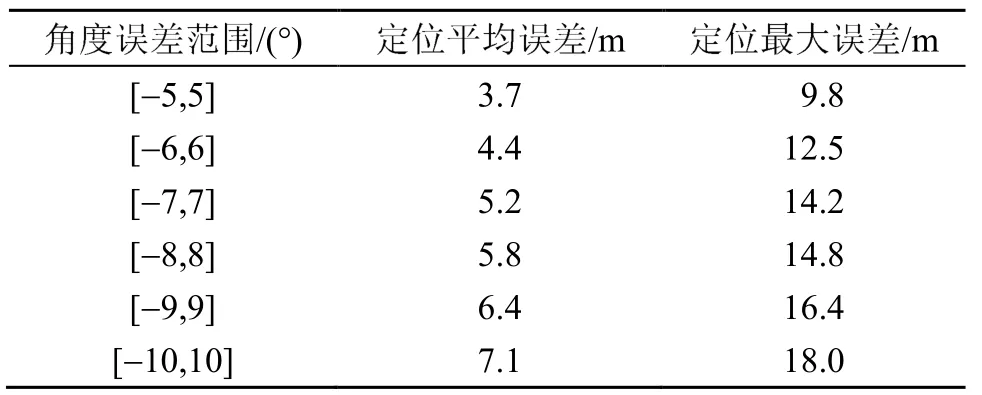
表2 1 000次蒙特卡洛仿真中軌跡估計的平均誤差與最大誤差 Table 2 Average error and maximum error of trajectory esti-mation in 1 000 times of Monte Carlo simulations

4 結論

本文針對高速飛行目標計算波達方位時由于目標高速運動，不同陣列所接收到的信號并非聲源在同一時刻所發出，難以在時間維度上進行對齊等問題，不可避免存在誤差。借鑒點云數據處理的思想，提出了一種基于空間匹配的高速飛行目標軌跡估計方法。對于單個陣列而言，對每一幀數據計算得到的波達方向在字典上進行匹配，找到誤差最小的N個空間點進行直線擬合。再對兩幀以上的數據所擬合的直線進行空間點采樣，得到空間點數據集，通過空間平面擬合，得到估計平面。兩個陣列解算得到的平面相交，相交直線即為高速飛行目標的軌跡估計結果。仿真結果表明：

（1）由于空間點直線擬合與平面擬合存在誤差，造成軌跡估計結果存在誤差。當陣列使用的數據幀數增加時，軌跡估計的誤差減小。

（2）該算法可以減小單次波達方向估計誤差對軌跡估計的影響。單陣列與雙陣列的陣列安裝誤差造成的軌跡估計誤差隨飛行高度的降低而減小。目標飛行高度為120.9 m 時，單陣列與雙陣列的陣列安裝誤差范圍為[? 2 °,2 °]，軌跡估計誤差小于10 m。對于隨機誤差，該算法表現出了較好的魯棒性。

仿真結果驗證了高速飛行目標的軌跡估計算法的有效性。