基于憶阻器陣列的下一代儲池計算*

任寬 張握瑜 王菲 郭澤鈺 尚大山?

1) (中國科學院微電子研究所,微電子器件與集成技術重點實驗室,北京 100029)

2) (西南交通大學超導與新能源研究開發中心,磁浮技術與磁浮列車教育部重點實驗室,成都 610031)

3) (中國科學院大學,北京 100049)

儲池計算是類腦計算范式的一種,具有結構簡單、訓練參數少等特點,在時序信號處理、混沌動力學系統預測等方面有著巨大的應用潛力.本文提出了一種基于存內計算范式的儲池計算硬件實現方法,利用憶阻器陣列完成非線性向量自回歸過程中的矩陣向量乘法操作,有望進一步提升儲池計算的能效.通過憶阻器陣列仿真實驗,在Lorenz63 時間序列預測任務中驗證了該方法的可行性,以及該方法在噪聲條件下預測結果的魯棒性,并探究憶阻器陣列阻值精度對預測結果的影響.這一結果為儲池計算的硬件實現提供了一種新的途徑.

1 引言

理解生物大腦中信息的加工、處理模式,并在此基礎上構建類腦計算硬件系統是現代信息科學的前沿研究之一[1].研究表明,生物大腦等效于一個復雜神經網絡動力學系統[2],其處理外界信息的機能依賴于神經網絡的動力學過程[3].如何理解大腦的神經動力學過程、構建類腦動力學系統,是類腦計算硬件系統實現的核心問題[4].自然界中的信息大部分是用時序數據來定義的.大腦的動力學系統受外部時序信號刺激,并將刺激產生的數據進行編碼和存儲[5,6],進而形成各類認知過程.循環神經網絡(recurrent neural network,RNN)[7]是一種具有短時記憶能力的神經網絡,其中的神經元通過具有環路的網絡結構,不僅可以接受其他神經元的信息,也可以接受自身的信息,從而使網絡具有處理時序數據的能力,因此,更加適合模擬大腦的動力學系統.當前,RNN 已經被廣泛應用于語音識別、自然語言處理等任務中.然而,由于梯度消失和爆炸問題[8],RNN 需要的超參數多,而且訓練過程復雜.因此,RNN 在硬件系統實現上依然面臨結構復雜、訓練時間長和能耗高等問題[9].

儲池計算(reservoir computing,RC)是RNN的一種簡化形式.RC 概念最初的提出是為了模擬生物大腦中具有大量循環連接的皮質紋狀體系統處理視覺空間序列信息的過程[10].隨后人們基于RNN 的框架,構建了統一的RC 計算框架[11?13](如圖1(a)).RC 的核心是一個被稱為“儲池”的循環神經網絡隱藏層.該網絡能夠將時序輸入信號轉換到高維空間中.經過高維轉換后,輸入信號的特征就可以更容易地通過簡單線性回歸方法有效讀出.目前,RC 在時序信號處理[14]、混沌動力學系統預測[15]等動力學系統學習方面有良好的功能.值得注意的是,與標準RNN 相比[16],RC 中只需要訓練輸出層權重,并且不需要反向傳播算法,有效避免了梯度消失問題,因此,可以有效降低訓練復雜度和訓練時間.

圖1 三種RC 結構 (a) 傳統RC 結構;(b) 單節點延時RC結構;(c) 非線性向量自回歸RC 結構Fig.1.Three types of RC frameworks:(a) Conventional RC;(b) RC using a single nonlinear node reservoir with time-delayed feedback;(c) NGRC,which is equivalent to nonlinear vector autoregression.

傳統RC 主要包括由Jaeger[11]提出的ESN 模型（echo state network）和Maass 等[13]提出的LSM（liquid state machine）模型,他們的結構都如圖1(a)所示,包含輸入、儲池和輸出三部分.ESN模型的儲池和LSM 模型的儲池都為基于RNN 框架,由多個神經元隨機連接而成的結構.所不同的是,ESN 模型中的神經元是離散時間人工神經元,而LSM 模型中的神經元是具有興奮性和抑制性的脈沖神經元.儲池計算模型結構(以ESN 為例)可以用以下公式描述:

其中,u(n)為輸入向量,n為離散的時間,f表示儲池層單元的非線性激活函數,Win為輸入連接儲池的權重矩陣,x(n)是所有離散時間人工神經元的回聲狀態向量,W為神經元間的連接矩陣,Wout為儲池連接輸出的權重矩陣,y(n)為輸出向量.儲池計算只需要訓練輸出權重矩陣Wout,其性能取決于儲池神經元間的連接矩陣W.當W的譜半徑小于1 時(即特征值的絕對值的最大項),對任意輸入都可以得到對應的回聲狀態屬性[17].節點的回聲狀態屬性等效于節點具備“衰退記憶”[18].人們從理論上證明了,由離散時間“衰退記憶”節點構成的RC 網絡在輸入有界的情況下具備動力學通用逼近能力[19].

這類RC 的硬件實現方法可大致分為兩種:一種方法是通過使用神經網絡硬件或神經形態計算技術實現,如用模擬電路[20]、FPGA（fieldprogrammable gate array）[21,22]、大規模集成電路[23]、憶阻器[24?26]等直接構造儲池中多個隨機連接的神經元.這種方法可靈活調整神經元間連接的拓撲結構以改善性能,但是構造神經元需要的器件眾多,并且計算中每一個時間步都需要進行大量計算以及存儲大量神經元的狀態.另一種方法是采用具備“衰退記憶”的物理節點代替隨機連接的神經元,構成儲池的動力學系統,如納米線網絡[27,28]、光學器件網絡[29]、易失性憶阻器網絡[30]等.這種方法利用物理節點的“衰退記憶”特性進行計算.儲池的存與算在節點網絡中同時進行.然而由隨機連接的物理節點構成的動力學系統無法調整節點連接的拓撲結構,故這種方法在面對不同任務時,RC 的性能具有一定的不穩定性.

為了提高RC 的性能,研究人員對RC 結構進行了多種改進(如多儲池計算[31]、進化儲池計算[32]等),以及將RC 與其他特征提取方法(如卷積神經網絡[33]、強化學習[34]、注意力學習[35]等)相結合.目前,傳統RC 及其改進方法已經成功地被應用于眾多領域,如生物醫學、聲音識別、無線電等[36].然而,由于儲池結構中神經元很多,神經元狀態存儲以及更新需要大量的硬件資源,并且由于神經元連接拓撲結構難以調整,導致儲池計算的參數優化困難.

RC 中神經元節點間相互作用產生的高維信號可以通過延時動力學系統來實現.其狀態方程描述為[37]

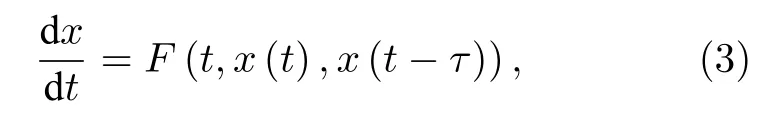
其中,t為連續時間信號,x(t)為系統的狀態,F為系統函數,τ為延時時間.2011 年,Appeltant 等[38]提出基于延時動力學系統的單延時節點RC 結構(見圖1(b)).輸入信號通過掩碼函數(masking)進行時間復用,然后輸入到單個物理節點在時間維度上展開的虛擬節點中.虛擬節點通過平等分割τ的N個時間點上來設置.兩個虛擬節點之間的時間間隔為θ=τ/N.所有虛擬節點x[t-(N-i)θ],i=1,···,N共同作為t時刻節點狀態,并通過輸出層得到計算結果.

單節點延時RC 的提出,使得RC 的硬件實現變得更加便捷,在一定程度上解決了傳統儲池硬件實現中,由于神經元數量多而導致的神經元狀態存儲和更新硬件資源問題.這種單節點延時儲池已經在光子器件[39]、FPGAs[40]中得到硬件實現,用于語音識別、圖像分類和混沌預測等任務中.我們在前期工作中,利用鐵電隧道結(FTJ)中超薄鐵電層的退極化效應產生的電流延時特性,實現了單節點延時儲池計算功能[41].為了拓展單節點延時RC功能,我們采用了多個單延時節點儲池并聯的方式,提高了計算的維度,實現了對動態數字序列的識別功能[41].然而,由于虛擬節點是通過時間切分獲得,所以其連接拓撲結構是按時間順序固定的.這意味著這種延時儲池同樣存在著參數優化困難的問題.

最近,Gauthier 等[42]提出了一種新型RC,稱為下一代儲池計算(NGRC).NGRC 是一種特殊的非線性向量自回歸過程,其等效于具有線性激活節點的儲池與一個非線性讀出層的結合,如圖1(c)所示.NGRC 模型描述為

其中,i為離散時間,Olin,i為線性特征向量,X(i)為第i時刻的輸入向量,s為時間間隔,k為構成線性特征向量的組數,Ononlin,i為第i時刻非線性特征向量,功能為將符號兩邊項進行外積、并收集外積結果的唯一單項式的運算符號,Ototal,i為第i時刻總特征向量,c為常數修正項,Y (i)為輸出值,Wout為儲池連接輸出的權重矩陣.NGRC 目前被證實在完成短期動態預測、長期混沌預測、推斷動力學系統不可見數據等三個方面有很好的性能.相對于傳統RC 和延時RC,NGRC 使用更小的數據集進行訓練,并避免了RC 的參數優化困難問題.然而,非線性向量自回歸過程本身仍需要大量硬件計算資源用于乘法計算操作.

憶阻器是近年廣受關注的一種具有記憶功能的器件[43].由憶阻器器件構成的交叉陣列[44],可以通過歐姆定律和基爾霍夫定律,以存內計算的方式原位、并行、物理地完成矩陣向量乘運算,有效減少了計算過程中數據的搬運,從而具有功耗低、速度快的優點[45?47].本文將NGRC 過程通過矩陣向量乘法操作簡化,提出了一種NGRC 的存內計算硬件實現方法,并利用憶阻器陣列完成矩陣向量乘法操作.通過進行憶阻器陣列仿真完成了Lorenz63時間序列預測任務,驗證了該方法的可行性,并研究了憶阻器件電阻精度和波動性對NGRC 預測精度的影響.這一結果為高能效RC 提供了一種新的途徑.

2 NGRC 的存內實現方法

傳統RC 過程中,每一個時間步都需要更新大量具有“衰退記憶”特性的神經元的狀態,然而具有“衰退記憶”特性的線性神經元組成的儲池與二次非線性讀出層組合,在數學上等效于一種特殊的非線性向量自回歸過程.NGRC 是對這種特殊的非線性向量自回歸過程的優化[42].NGRC 過程與傳統儲池計算過程的相同點在于都只需要訓練輸出權重,但是在輸入數據的選擇和將輸入數據進行高維空間非線性轉換的方式上有所不同.

輸入數據方面,傳統儲池輸入數據一般為當前時刻的數據,而NGRC 的輸入數據中,除了當前時刻的數據,還包括之前時刻所對應的數據.高維空間非線性轉換方式方面,傳統儲池的高維空間非線性轉換通過儲池中具備“衰退記憶”神經元的非線性激活函數達成.NGRC 結構儲池的高維空間非線性轉換可分為3 個過程(見圖1(c)):1) 選擇不同時刻輸入數據構成線性特征向量Olin;2)由線性特征向量構造非線性特征向量Ononlin;3) 由線性特征向量與非線性特征向量構造總特征向量Ototal.3 個過程中,線性特征Olin向量是由選擇的輸入數據直接拼接而成;總特征向量Ototal是由固定常數c、線性特征向量Olin與非線性特征向量Ononlin直接拼接而成;而由線性特征向量Olin構造非線性特征向量Ononlin則需要經過一個非線性轉換過程.NGRC中的非線性轉換過程將線性特征向量Olin通過外積操作映射到一個高維空間中,并在高維空間中去除對應映射向量的重復部分,得到非線性特征向量Ononlin.

NGRC 的非線性轉換過程雖然避免了傳統儲池中隨機連接的性能不確定性與需要同時更新多個神經元狀態的復雜性,但其向量間的外積操作與除去高維向量重復部分的操作仍然需要大量硬件開銷與時間開銷.我們注意到相同向量間的外積可以用矩陣向量乘法(matrix vector multiplication,MVM)來表示,去除重復映射向量的操作可以通過保留外積后固定位置元素的值(保留元素操作)來實現.硬件上,使用憶阻器陣列進行MVM 操作,使用憶阻器陣列的選擇線電路進行保留元素操作.

2.1 線性特征向量的構建

圖2(a)為三維空間時序數據預測任務的NGRC儲池的存內實現結構.其中,ti=i×Δt,Δt為采樣間隔,i為離散時間數,s為時間間隔數,x(t),y(t),z(t)分別表示預測點在t時刻的x軸、y軸、z軸三維空間坐標,k為每個線性特征向量所取數據的組數.當已知ti時刻及之前時刻點的軌跡坐標,要預測ti+1時刻點的坐標時,取k=2,即令ti時刻和ti-s時刻空間點的三維坐標構建第i個線性特征向量Olin,i,有

其中,[xi,yi,zi]與[xi-s,yi-s,zi-s]為ti時刻與ti-s時刻點的三維坐標.將構建的線性特征向量Olin,i用時序電壓脈沖幅值編碼和電導編碼,編碼的電壓序列矩陣Vlin,i為

其中列向量Vlin,i,a的第a行的值,為線性特征向量Olin,i中第a個元素對應的量化電壓值,列向量中的其他值為零.線性特征向量Olin,i編碼的電導矩陣為

其中,Glin,i,a為Olin,i中的第a個元素對應的量化電導值.將電導序列使用差分編碼存儲到憶阻器陣列中;再將電壓序列Vlin,i通過Bitline 輸入到憶阻陣列中,具體過程如圖2(b)所示.需要指出的是,電壓脈沖幅值編碼需要經過一個數模轉換器(DAC).DAC 的精度與憶阻器本身的精度影響著整體精度.

2.2 非線性特征向量的構建

構建非線性特征向量需要對線性特征向量進行外積操作與保留元素操作.憶阻器陣列中,每通過一個電壓序列向量Vlin,i,a,能從陣列輸出端(SL)得到一個電流向量Ilin,i,a,總電流矩陣由歐姆定律和基爾霍夫定律可表達為

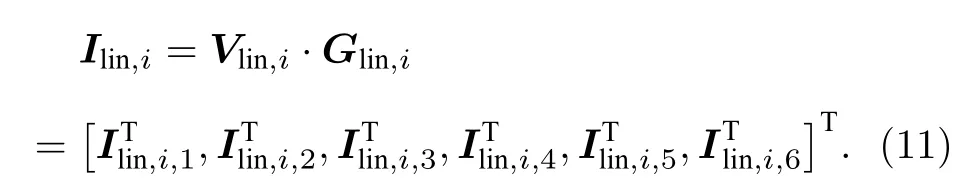
保留Ilin,i矩陣中的非零元素,Ilin,i,a保留元素操作后的向量為Ilin,i,ap,保留元素操作可通過只讀取憶阻器陣列電流輸出中對應位置的輸出實現,過程如圖2(a)中綠框部分所示,將選擇讀取的輸出電流組成非線性特征向量Ononlin,i,可表達為

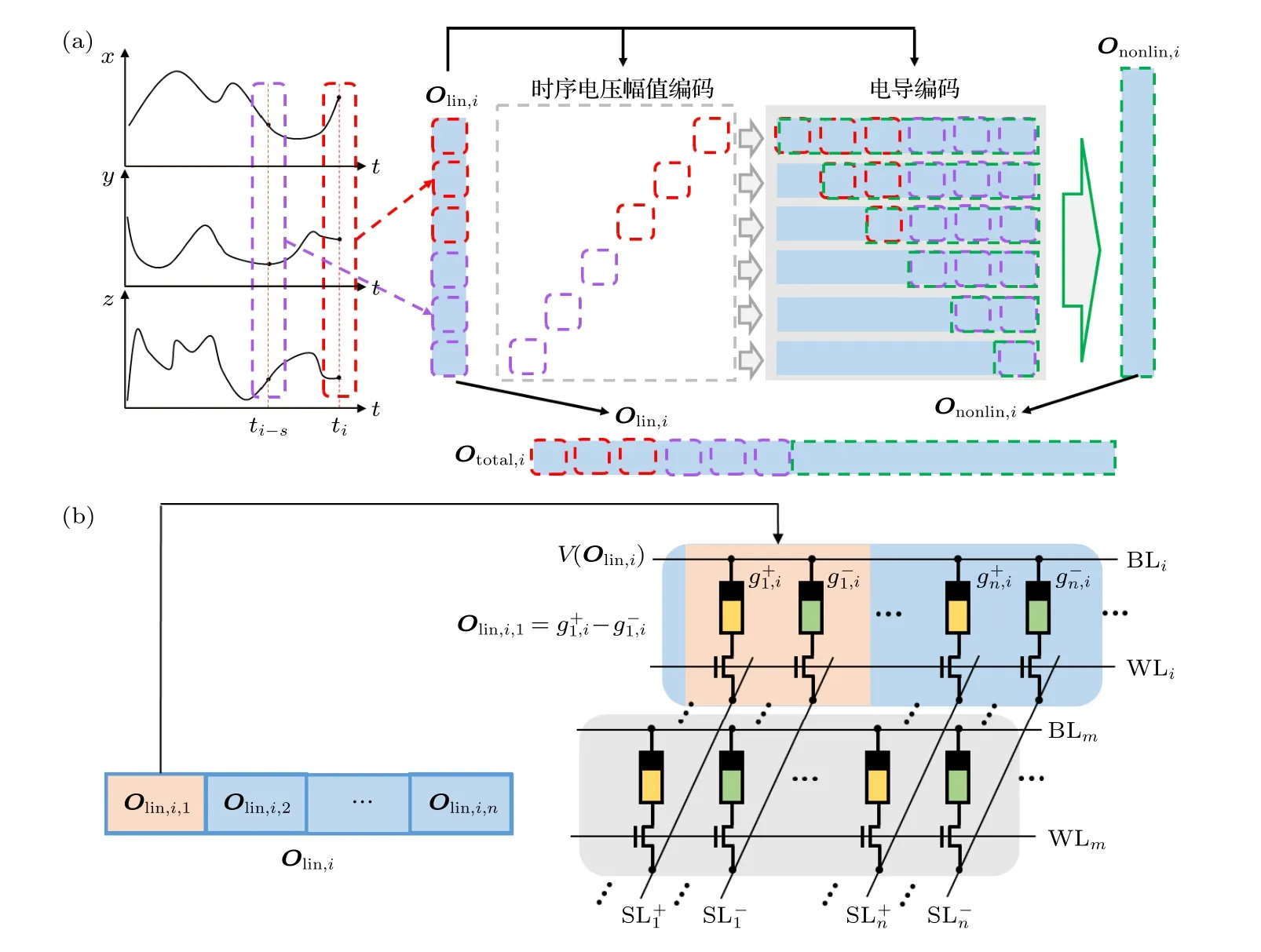
圖2 基于憶阻陣列的NGRC 儲池結構 (a)用于預測三維時序信號的NGRC 儲池結構.輸入為三維時序信號;提取ti 時刻(紅色框)和ti-s(紫色框)時刻信號的值組成線性特征向量Olin,將第i 個線性特征向量編碼為時序電壓和電導,時序電壓作為憶阻器陣列的輸入,電導映射到憶阻器陣列上作為權重;非線性特征向量Ononlin由憶阻器陣列特定單元(綠色方框)的輸出構成;總特征向量由Olin與Ononlin直接拼接而成.(b) 圖(a)中的線性特征向量Olin,i映射到憶阻器陣列的方式.Olin,i中的每一個值都由兩個憶阻器電導的差分g+,g–表示Fig.2.Structure of the NGRC based on memristor-based crossbar.(a) Structure of the NGRC reservoir for three dimensional (3D)timing signals predicting.The input is a 3D timing signal.The linear feature vector Olin is formed by extracting the signal values of ti time (red box) and ti-s time (purple box).The ith linear feature vector is encoded as timing voltage and conductance,and the timing voltage is the input of the memristor array,and the conductance is mapped to the memristor array as weight.The nonlinear feature vector Ononlin consists of the outputs of specific elements of the memristor array (green boxes).The total feature vector is directly spliced by Olin and Ononlin.(b) The way the linear feature vector Olin, i in panel (a) mapping to the memristor array.The g+and g– represent the device conductance values for the positive and negative weights in the differential pair,respectively.

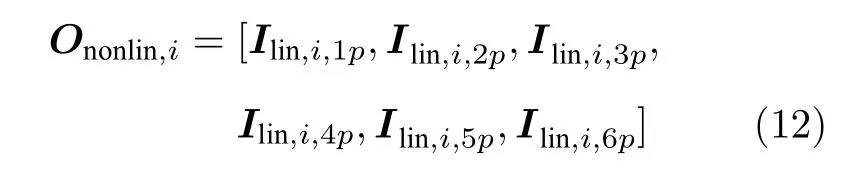
2.3 總特征向量的構建及輸出

ti時刻的總特征向量Ototal,i是由固定常數c、線性特征向量Olin,i與非線性特征向量Ononlin,i直接拼接而成,表示為

ti+1時刻點的預測位置可直接由總特征向量乘以輸出權重得出:

其中,[xi+1,yi+1,zi+1]為所預測的ti+1時刻點的三維坐標,Wout為預先用嶺回歸方法訓練好的輸出權重矩陣.值得注意的是,憶阻器電流值的讀出需要一個模數轉換器(ADC),ADC 的精度也會對最終預測精度造成一定影響.

2.4 訓練過程

儲池訓練過程只訓練輸出層Wout,訓練采用嶺回歸方法,先用訓練數據集得到由特征向量組成的特征矩陣Ototal,以及所有特征向量對應的輸出組成的結果矩陣Yd,嶺回歸方法表達為

2.5 仿真平臺

仿真平臺基于python 3.8,pytorch1.9.1(主機GPU 型號NVIDIA GeForce RTX 3080,CPU 型號i9-11980HK)構建,其結構示意圖如圖3 所示,可分為輸入部分、權重部分和輸出部分.

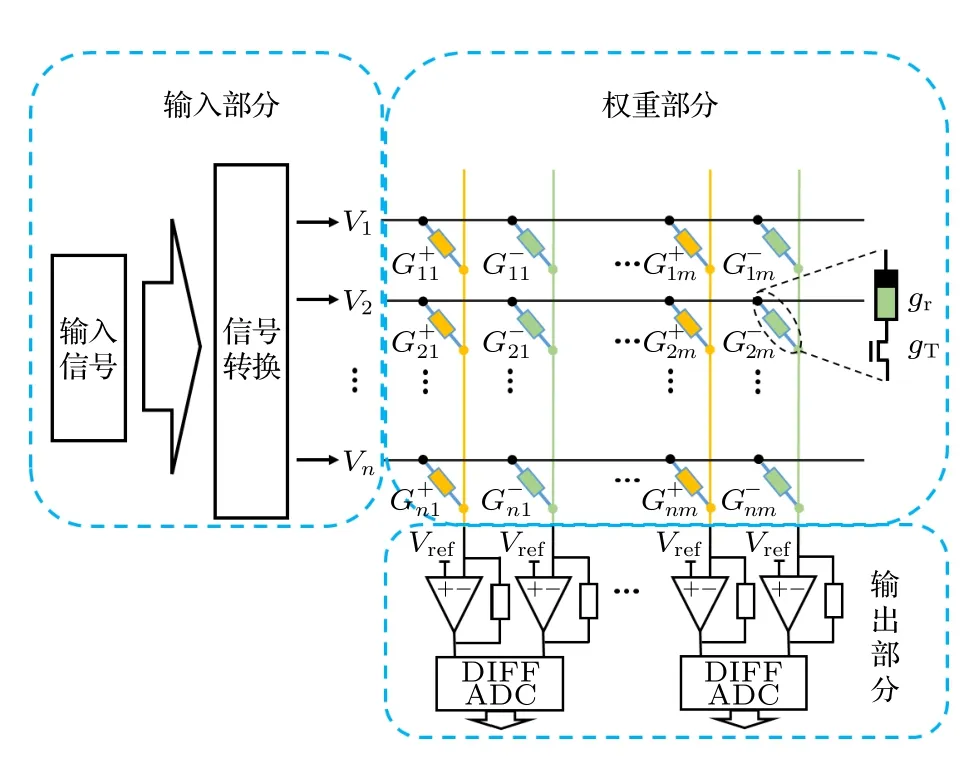
圖3 基于憶阻器陣列(包括正、負列)的矩陣乘法運算仿真平臺結構示意圖,gr 為憶阻器的電導,gT 為晶體管電導Fig.3.Simulation platform of memristor array (including positive and negative arrays) as analog dot-product engine.The memristor conductance corresponds to gr and the transistor conductance corresponds to gT.

輸入部分模擬將外界信號轉換為電壓信號的過程,最高轉換精度為定點32 bit.權重部分模擬將外界信號映射到憶阻器陣列中(將帶符號的權重映射到一對憶阻器差分電導上)并進行運算的過程,量化電導映射公式為

其中n為權重精度(單位 bit),Gmax和Gmin為憶阻器可變化的最大電導與最小電導,[x]為取整操作,W為需要映射的權重,G為映射到憶阻器陣列對應位置的電導值.輸出部分模擬憶阻器陣列輸出經過ADC 轉變為電腦可處理數據的過程,輸出精度為所使用ADC 的精度.

3 實驗結果與討論

動力學系統的短期預測能力與動力學系統的長期預測能力通常被用來作為衡量RC 性能的基準,我們將用經典混沌動力學系統模型-Lorenz63模型的短期預測任務與長期預測任務,驗證基于憶阻器陣列實現的NGRC 結構的可行性及其對噪聲的魯棒性.Lorenz63 是1963 年洛倫茲[48]提出來的天氣預測模型,由3 個方程組成:

其中狀態X(t) ≡ [x,y,z]T是一個分量為Rayleigh-Bénard 的對流可觀測量的矢量,a=10,b=28,c=8/3.Lorenz63 模型確定性的混沌行為體現在其對初始條件的敏感依賴(蝴蝶效應),以及在相空間軌跡形成奇異吸引子(圖3).

動態系統的預測任務中,用原序列(由動態系統方程得到的序列)與預測序列(儲池不斷將此時刻輸出值作為下一時刻的輸入值進行預測得到的序列)之間的結構相似度來衡量預測效果.就Lorenz63 時間序列預測任務而言,歸一化均方根誤差(NRMSE)可在一定程度上衡量短預測期內的結構相似度,但難以反映長期預測的結構相似度.Lorenz63 時間序列預測的z回歸圖能直觀地反映z變量的長期行為,比較原序列與預測序列的z回歸圖可以定性地比較兩個序列長時段的結構相似度.在之后的Lorenz63 時間序列預測任務中,NRMSE衡量短期預測(1 個李雅普諾夫周期)的結構相似度,通過比較量原序列與預測序列的z回歸圖衡量長期預測的結構相似度.

在基于憶阻器陣列實現的NGRC 結構的可行性驗證實驗中,維持系統的輸入精度不變,通過改變系統的權重精度(憶阻陣列中憶阻器的量化映射比特數)和輸出精度(憶阻器陣列輸出ADC 比特數),研究不同權重精度和輸出精度對預測結果的結構相似度的影響.在基于憶阻器陣列實現的NGRC結構對噪聲的魯棒性驗證實驗中,維持輸入精度和輸出精度不變,研究不同權重精度以及不同噪聲大小對預測結果的結構相似度的影響.

3.1 可行性驗證實驗

保持輸入精度為定點32 bit,輸出精度為定點64 bit,在權重精度為4,6,8,16,32 和64 bit 情況下進行預測實驗.800 個時間步的預測結果及其xz截面圖如圖4 所示.可以看出,權重精度在4 和6 bit 時無法產生混沌現象(無洛倫茲吸引子);當權重精度達到8 bit 及以上時,開始產生明顯的洛倫茲混沌吸引子.這一結果意味著權重精度對混沌的產生有重要影響.當憶阻器陣列對應的權重精度達到一定值時,基于憶阻器陣列實現的NGRC 結構構成的系統能由穩定狀態過渡到混沌狀態.

圖4 輸入精度為定點32 bit,輸出精度為定點64 bit,不同權重精度下800 個時間步的預測XZ 截面圖 (a) 64 bit;(b) 32 bit;(c) 16 bit;(d) 8 bit;(e) 6 bit;(f) 4 bitFig.4.The XZ cross sections of 800 time steps with different weight precision,when input precision of integer is 32 bit and output precision of integer is 64 bit:(a) 64 bit;(b) 32 bit;(c) 16 bit;(d) 8 bit;(e) 6 bit;(f) 4 bit.

保持輸入精度為定點32 bit,通過改變權重精度以及輸出精度,在達到混沌狀態的前提下探究短期預測結構相似度與權重精度的關系.圖5 為短期預測(1 個李雅普諾夫周期)的NRMSE 隨不同權重精度(8,16,32,64 bit)和不同輸出精度(8,16,32,64 bit)的變化.結果顯示,當基于憶阻器陣列實現的NGRC 結構構成的系統達到產生混沌所需的權重精度和輸出精度時,短期預測的性能隨著權重精度、輸出精度的增加而增加.在權重精度不變的情況下,當輸出精度達到16 bit,輸出精度的增加對短期預測結構相似度幾乎無影響;在輸出精度不變的情況下,短期預測結構相似度隨著權重精度的增加而變高(NRMSE 變小),8 bit 權重精度下的NRMSE 低于0.05,16 bit 權重精度下的NRMSE接近于0,當權重精度超過16 bit 時,權重精度的增加對短期預測結構相似度幾乎無影響.

圖5 短期預測(1 個李雅普諾夫周期)的NRMSE 隨不同權重精度(8,16,32,64 bit)和不同輸出精度(8,16,32,64 bit)的變化Fig.5.The variation diagram of NRMSE for short-term prediction (1 Lyapunov cycle) with different weight precision (8,16,32,64 bit) and different output precision (8,16,32,64 bit).

Lorenz63 系統的z分量在連續的局部極大值之間具有函數關系,通過找到z分量的連續局部極大值Mi并根據Mi+1畫出Mi形成z回歸圖,可以簡潔地展現z變量的長期行為.Lorenz63 系統的z回歸圖如圖6 所示,紫色點為真實序列z回歸圖,其他顏色為輸入精度為定點32 bit,輸出精度為定點64 bit,權重精度分別為8,16,32,64 bit 的z回歸圖.結果顯示,權重精度為8 bit 時的z回歸圖相比真實序列的回歸圖有明顯偏移;當權重精度在16 bit 及以上時,預測的回歸圖幾乎完全覆蓋了真實序列的回歸圖;隨著權重精度的增加,預測的回歸圖往真實序列的回歸圖收斂.

圖6 (a) Lorenz63 的z 回歸圖(紫色)與不同權重精度下預測的z 回歸圖;(b)圖(a)紅框區域標記中的放大圖Fig.6.(a) The z return map of Lorenz63 (purple) overlaid with the z return map under different weight accuracy;(b) detail of the region marked in Fig.(a).

3.2 噪聲魯棒性驗證實驗

在保持輸入精度為定點32 bit,輸出精度為定點64 bit,給權重(即憶阻器電導G)添加高斯噪聲NoiseN(0,σ),其中σ=G×10-4×percent為方差,percent 表示噪聲強度百分比.短期預測結構相似度的NRMSE 隨權重噪聲強度變化的結果如圖7所示.當權重精度在8 bit 時,隨著σ的增大,短期預測結構相似度的NRMSE 會先降低后升高;當權重精度在16 bit 時,短期預測結構相似度的NRMSE也會先降低后升高,但降低點對應的噪聲強度比權重精度在8 bit 時小;當權重精度在16 bit 以上時,短期預測的NRMSE 會隨著percent 的增大而增大.由于量化本身具備一定的抗噪聲能力,故權重精度越低,噪聲對短期預測結構相似度的NRMSE的影響越小;值得注意的是,一定程度的噪聲有利于提升短期預測性能,并且量化的比特數越高,能帶來增益的噪聲強度越小.

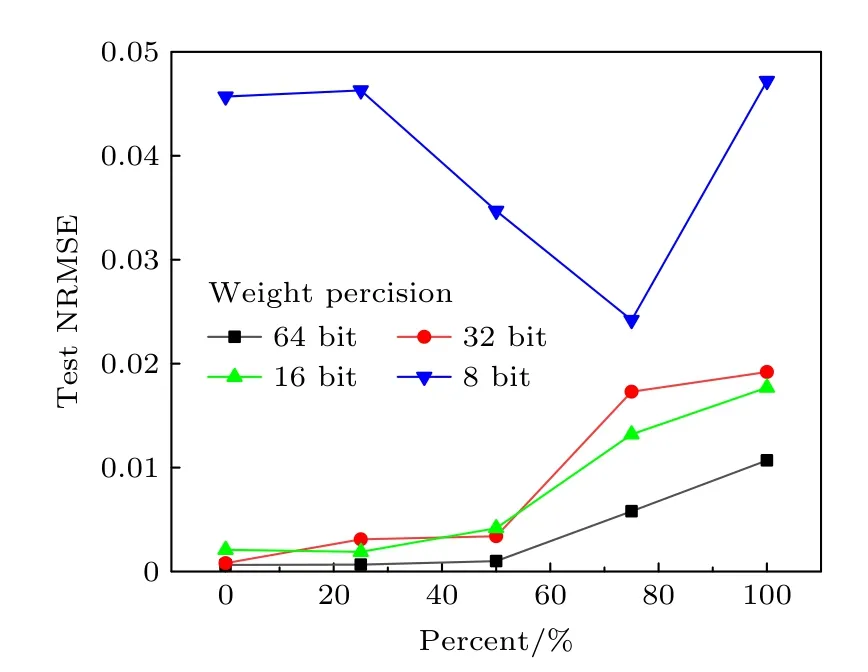
圖7 短期預測結構相似度的NRMSE 在不同權重精度條件下隨權重噪聲強度的變化Fig.7.The variation of NRMSE under different weight precision conditions for short-term prediction with increasing weight noise intensity.

3.3 討論

基于憶阻器陣列的NGRC 存內實現具備兩方面的優勢:第一,就NGRC 算法本身而言,相對于傳統儲池計算和基于延時的儲池計算,NGRC 的儲池具備更短的激活時間、更少的參數訓練量以及更快的訓練和推理速度[42];第二,就存內計算方面而言,NGRC 中提取非線性特征向量的過程需要大量的乘法操作,而憶阻器陣列相比傳統CMOS電路,在矩陣向量乘法方面具備更快的計算速度和更低的功耗[49].然而,使用憶阻器陣列進行NGRC的過程中,每一次推理過程都需要在憶阻器陣列中寫入采樣數據;同時,仿真結果表明,憶阻器陣列中每個憶阻器精度達到8 bit,Lorenz63 才能有較好的預測結果.考慮到當前憶阻器還存在各種非理想性因素,因此,如何進一步提高寫入效率,同時降低所需憶阻器的阻值精度還需進一步探索.

4 結論

儲池計算自提出至今可以分為傳統儲池計算、延時儲池計算和下一代儲池計算三個階段.儲池計算性能上的優勢不僅來自于算法自身,而且與硬件的實現方式密切相關.本文在總結儲池計算發展歷程的基礎上,提出一種基于存內計算范式的硬件實現方法,將NGRC 過程通過矩陣向量乘法操作簡化,并利用憶阻器陣列完成矩陣向量乘法操作.憶阻器陣列仿真實驗驗證了這一方法在Lorenz63 三維時間序列預測任務中的可行性.仿真實驗結果表明,預測效果與輸出精度和權重精度密切相關.當輸出精度達到16 bit,進一步提高輸出精度對預測效果的影響可忽略不計,并且具有良好的抗噪聲能力;當權重精度達到8 bit,對Lorenz63 三維時間序列預測的短期預測(1 個李雅普諾夫時間)就可以有良好的預測效果(NRMSE 小于0.05),并可以在一定程度進行長期預測.這些結果為NGRC 的硬件實現提供了一種新的途徑,同時也展現了憶阻器陣列在開發基于儲池計算的實時、低能耗邊緣計算系統方面的潛力.