三維Boussinesq型水波方程的改進
劉忠波, 劉澤, 王鋮龍, 王彥, 房克照
(1.大連海事大學交通運輸工程學院, 大連 116026; 2.大連理工大學海岸和近海國家重點實驗室, 大連 116024)
Boussinesq型水波方程是一類時域水波模型,此類模型最顯著的基本特征是控制方程中變量不對垂向坐標z求導,等同于將三維波浪問題降至水平二維問題,同時Boussinesq模型也無需追蹤自由面問題,從而大大降低了計算時間,這促進了其在海岸波浪水動力模擬研究的廣泛應用。
考慮到模型在實際工程應用的可能性,Boussinesq型水波方程的變量對空間坐標求導一般不超過3,關于這一點,很多理論和數值應用文獻均有陳述[1-4]。吳昕煒等[5]利用Boussinesq波浪(Boussinesq wave,BW)模型對波浪在實際地形中的傳播變形規律進行了數值模擬研究,并利用相關試驗結果進行了驗證,該模型最高空間導數為3。最高空間導數為2的弱非線性Boussinesq型水波方程由Zhao等[6]給出,該方程具有Padé(2,2)的色散性能,一些學者研究泥沙動力學問題前選擇了這個模型開展相關的波浪水動力研究,但弱非線性是該模型的主要限制。Liu等[2]、Chazel等[7]給出最高空間導數為2的多層三維Boussinesq水波方程;Liu等[8]進一步分析了Liu等[2]多層方程的理論性能,多層模型顯著提高了方程的線性和非線性性能。作為代價,層數越多,計算時間也會相應增加。Liu等[8]模擬水槽聚焦波算例的結果表明,3層(11個方程)比2層(9個方程)計算時間增約為23%。因此,選擇單層模型也具有研究價值,盡管在1%色散誤差下原方程的適用最大因次水深kh=3.8,但精確的色散關系僅在kh<1.23左右(0.1%誤差)。與色散性能更為優良的多層模型不同,單層模型在實際工程中被選擇應用的概率更大,因此有限水深時的性能更應予以重視。
除色散性外,淺化和非線性等性能是推導Boussinesq型水波方程必須檢測的重要指標[2,8-10]。以變淺性能為例,劉忠波等[11]對水平二維Boussinesq方程[9,12-13]中的速度用變換速度取代,并通過分析變淺性能獲取了相關參數值。事實上,變換速度中引入水深變化項使得控制方程含有的獨立色散參數和獨立變淺參數的個數相等,這是方程具有更優良變淺性能的關鍵因素。與水平二維方程不同,三維Boussinesq型方程含垂向速度,確保了方程具有更優良的非線性性能[2,7-8,14]。
為了平衡效率和模型精度,現選擇Liu等[2]給出最高空間導數為2的單層三維Boussinesq水波方程為研究對象,對其理論性能的改進方面進行初探,并建立相應的數值模型,通過相關試驗來驗證理論模型的改進。
1 三維Boussinesq型方程的改進
Liu等[2]在無旋、無黏假設下,首先沿垂向方向將水體分為N層,并規定每層中點水深處的速度為特征速度,在每一層中,對該特征速度關于z做泰勒展開,并利用連續方程和無旋假定,則可消除掉變量對垂向坐標z的導數,可以得到一組以N層特征速度表達的Boussinesq型水波方程。其次,對N個特征速度變量引入L變換算子得到N個變換速度(又稱為偽速度或計算速度),引入變換速度的核心目的是提高方程的色散性,最終推導出具有更高性能的三組N層Boussinesq型水波方程。選取最高導數為2的單層方程作為研究對象,方程中的主要變量為波面位移η、自由表面處水平和垂向速度uη和wη、靜止水位處的速度u10和w10以及變換速度uE和wE。
在自由表面處,精確的運動學和動力學邊界條件為

(1)

(2)
U=uη+wη?η
(3)
式中:U為定義在自由表面處速度勢的水平梯度;g為重力加速度;?為水平梯度算子。
在海底,邊界滿足條件為
ub·?h+wb=0
(4)
式(4)中:ub和wb分別為海底水平速度和垂向速度;h為靜止水位下的水深。
自由表面處速度與靜止水位處速度滿足的關系表達式為
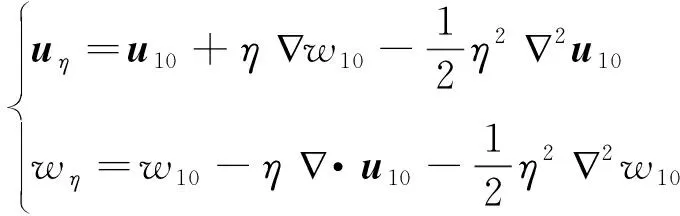
(5)
從水底到靜止水平面的速度場可表達為

(z-zα)?zα?·uE+(z-zα)?wE+

(6)

(z-zα)?zα·?wE-(z-zα)?·uE-

(7)

將z=0和z=-h分別代入式(6)和式(7)可得到靜止水位處和海底處的速度。在式(6)和式(7)中,引入的變換速度(uE,wE)與靜止的中間水深處速度(uα,wα)之間的L變換表達式為

(8)

(9)
與式(8)和式(9)給出的L變換表達式不同,引入的變換如下。
uα=uE+α1(αh)2?(?·uE)+β1α2h?h?·uE
(10)
wα=wE+α2(αh)2?·(?wE)+β2α2h?h·(?wE)
(11)
式中:α1、α2為色散參數;β1、β2為變淺參數。
由此,速度場表達式為

(z-zα)?zα?·uE+(z-zα)?wE+
[-2α2(z-zα)αh+(z-zα)2]?zα?·
(?wE)+β1α2h?h?·uE+
β2α2h(z-zα)?h?2wE
(12)

(z-zα)?zα·?wE-(z-zα)?·uE-
[-2α1(z-zα)αh+(z-zα)2]?zα·
?(?·uE)+β2α2h?h·(?wE)-
(z-zα)β1α2h?h·?2uE
(13)
類似于文獻[10],在水底方程中引入變淺系數β3,最終水底運動學方程可寫為




(14)
式(1)、式(2)、式(5)、式(14)以及靜止水位處速度與變換速度的表達式[z=0代入式(12)和式(13)],構成了新三維Boussinesq型水波方程,當α1=α2=1/6,β1=β2=0時,則可以轉化為原來的方程。
2 方程的基本性能
在立面二維和常水深情況下,通過傅里葉分析,則可分析出方程的相速度、和差頻、速度分布特征等,分析的詳細過程參見文獻[10]。
2.1 相速度
方程的色散關系表達式可寫為

(15)
式(15)中:ω為波浪圓頻率;k為波數。
當表達式(15)確定的相速度與解析相速度在0 圖1 無因次相速度Fig.1 Non-dimensional wave phase celerity 為了表征速度分布的精度,采用Madsen等[14]給出的公式考察本文方程與解析解之間的誤差,公式為 (16) 式(16)中:us(0) 和ws(0)分別為z=0時的Stokes波線性解。圖2給出了改進值與原參數下的速度分布誤差的比較,整體來看,改進參數后的水平速度和垂向速度誤差更小。 圖2 速度分布誤差Fig.2 The error of the velocity profiles 一般來說,對于不含垂向速度的Boussinesq水波方程,差頻性能是核心短板,關于這一點,文獻[9,12,15]中均有表述。當選取色散參數α1=0.170,α2=0.158(改進值)和α1=α2=1/6(原參數)情況下的,Boussinesq方程的和差頻解析結果如圖3所示,其中,k1和k2是兩個不同頻率波浪的波數。無因次和頻和差頻均以對角線為對稱線,對角線上面部分為和頻,下面部分是差頻,圖3僅給出一半的圖形。改進后,1%誤差下和頻、差頻適用范圍均超過了kh=4。1%誤差下原參數方程的和頻、差頻適用范圍僅約等kh=1.7和kh=2.2。這表明,本文方程具有更優良的和差頻特性。此外,無論是原方程還是本文方程,在非線性性能方面特別是差頻性能方面均優于傳統型的Boussinesq水波方程,以Gobbi等[16]的方程為例進行說明,該方程精確到4階保留了所有非線性項,色散適用水深約為kh=6,其1%誤差下差頻的適用范圍僅為kh=1左右。 圖3 無因次和差頻Fig.3 Non-dimensional amplitudes of sub-harmonics and super-harmonics 變淺性能代表著線性波浪由深水到淺水演化過程中的淺化特征,在0 圖4 方程的變淺梯度Fig.4 The shoaling gradient of the present model 對Boussinesq型水波方程可構建相應的垂向二維模型,數值模型中對時間差分采用3階Adams-Bashforth格式和4階Adams-Moulton格式,分別用于預報和校正階段。當預報和校正的所有變量的誤差控制在一定范圍內,則當前計算步結束。波浪的產生采用Hsiao等[17]的域內造波法,并在兩邊界上采用2倍波長的海綿邊界層進行消波。 為對比改進前后模型的差別,選擇了對Luth等[18]潛堤上規則波傳播變形的試驗數值模擬。先簡要分析波浪在潛堤上的演化過程,波浪的傳播變形是一個復雜的物理過程,其演化過程中主要包括波-波相互作用、變淺與反變淺、相位鎖定與解鎖甚至波浪破碎等。為了精準模擬演化過程,數值模型應具有足夠精度的色散性、變淺性和非線性性能。 圖5 計算波面位移與文獻[14]試驗結果的比較Fig.5 The comparisons of the computed surface elevations with reference[14] 數值模擬中,選取了周期T=2.02 s,波高為0.02 m的工況,時間步長采用0.01 s,空間步長采用0.03 m。圖5所示為改進前與改進后的計算波面位移與實驗結果的比較。改進后的本文方程和原方程的模擬結果與實驗結果吻合程度均較高,但在浪高儀位置x=19.0 m和x=21.0 m處,本文方程比原方程在3次峰波形的準確性上更高。具有Padé (2, 2)色散關系的各種Boussinesq數值模型無法準確捕捉到最后3個位置點的波面位移。具有Padé (4, 4)色散關系的方程,若變淺性和非線性性能足夠,則可以較為精確捕捉到這3個位置點的波面,倘若變淺性能不佳,則也無法精準模擬這一過程[19]。 通過引入帶參數的變換速度,導出了一組最高空間導數為2的三維Boussinseq型方程。并進行了理論分析和潛堤上波浪傳播變形模擬研究,主要得出以下結論。 (1)本文方程比原文獻在線性(相速度和速度分布)、和差頻等方面均有不同程度的改善,特別是相速度與解析解在0 (2)以實驗結果為標準,潛堤后方高次諧波釋放,原方程對三次峰的捕捉不夠精確,這反映出原方程在色散性精度不足,但值得注意的是,本文方程模擬的主峰與實驗結果吻合程度在最后兩個浪高儀位置與實驗結果的吻合程度略次于原方程,關于這一點,更廣泛的數值模擬驗證將會在下一步研究中進行。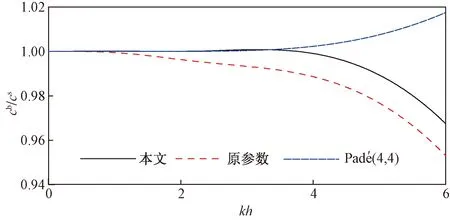
2.2 速度分布


2.3 不規則波中的和差頻

2.4 變淺性能

3 數值驗證

4 結論

