智能反射面輔助的無人機無線攜能通信網絡吞吐量最大化算法研究

劉志新 趙松晗 楊 毅 袁亞洲

(燕山大學電氣工程學院 秦皇島 066004)

1 引言

未來智慧城市的發展和大規模低功耗物聯網技術的應用，將導致無線終端節點數量的激增。然而，復雜的通信環境以及終端用戶能量受限等問題，將極大制約其發展。為此，無人機(Unmanned Aerial Vehicle, UAV)由于其高機動性和靈活性，在復雜的通信網絡中得到了廣泛的應用。目前針對UAV通信網絡的研究已取得了很多有價值的結果，文獻[1]中，UAV同時作為移動的數據收集者與能量供應者，通過聯合優化UAV的時間分配和軌跡設計，最大化多UAV無線供電網絡中的上行鏈路傳輸速率。文獻[2]研究了UAV最小能耗問題，并通過優化UAV懸停位置，最終實現系統的整體節能優化。以上工作證實了UAV路徑的合理設計是系統提升系統性能關鍵因素之一。然而，在復雜的通信環境中，如城市建筑密集區，UAV與地面用戶(Ground Users, GUs)之間的直接鏈路可能會受到障礙物的遮擋，從而嚴重影響通信質量。

智能反射面(Intelligent Reflecting Surface,IRS)技術由于其低功耗、高能效、可重構傳輸環境等特點，已受到學術界和工業界的廣泛關注[3]。IRS由一系列離散反射元件組成，每個反射元件都能獨立地反射入射信號。在微處理器的控制下，所有反射元件可以調控其入射信號的振幅和相移，從而達到理想的多徑效果[4]。為解決復雜環境中UAV與GUs間通信鏈路受阻問題，將IRS融入現有的UAV系統中將成為有效的解決方案。文獻[5]針對IRS輔助下的UAV通信網絡，聯合優化IRS相移和UAV飛行軌跡，研究了系統最大化安全速率問題。文獻[6]研究了IRS輔助下的邊緣計算(Mobile Edge Computing, MEC)場景，其中UAV作為空中的MEC服務器。仿真結果表明，IRS的輔助可以有效降低系統總能耗。

然而，上述工作并沒有考慮IRS以及GUs的能源受限問題。事實上，雖然IRS以其低功耗的特性為人熟知，當反射單元數量的提升，便不再可以忽略IRS的能耗[7]。然而，使用傳統布線或電池供應方案為IRS供電，不僅會增加維護成本，而且不便于IRS的靈活部署，難以應用到通信環境較為惡劣的場景。因此無線能量收集(Wireless Energy Harvesting, WEH)技術可成為上述問題的解決方案。綜上所述，本文基于城市環境中，提出一種新型的IRS輔助的UAV通信系統，通過適當部署IRS，以解決UAV與GUs間通信鏈路受阻問題。同時，IRS與GUs可以利用WEH從UAV的射頻信號中收集能量。本文的主要貢獻點如下：(1)本文建立了IRS輔助下UAV無線供能通信模型，通過聯合優化IRS的相移、GUs的發射功率和時間分配以及UAV路徑規劃，提升系統總吞吐量。(2)本文提出一種基于塊坐標下降法(Block Coordinate Descent,BCD)的資源分配算法來求解上述耦合且非凸的問題。其中，通過引入松弛變量、1階泰勒表達式和連續凸近似(Successive Convex Approximation,SCA)的方法將非凸的子問題轉化為凸問題進而求解。(3)數值仿真證明了本文所提算法具有較好的收斂性，并且與對比算法相比，可獲得更高的總吞吐量。

2 系統模型及問題描述

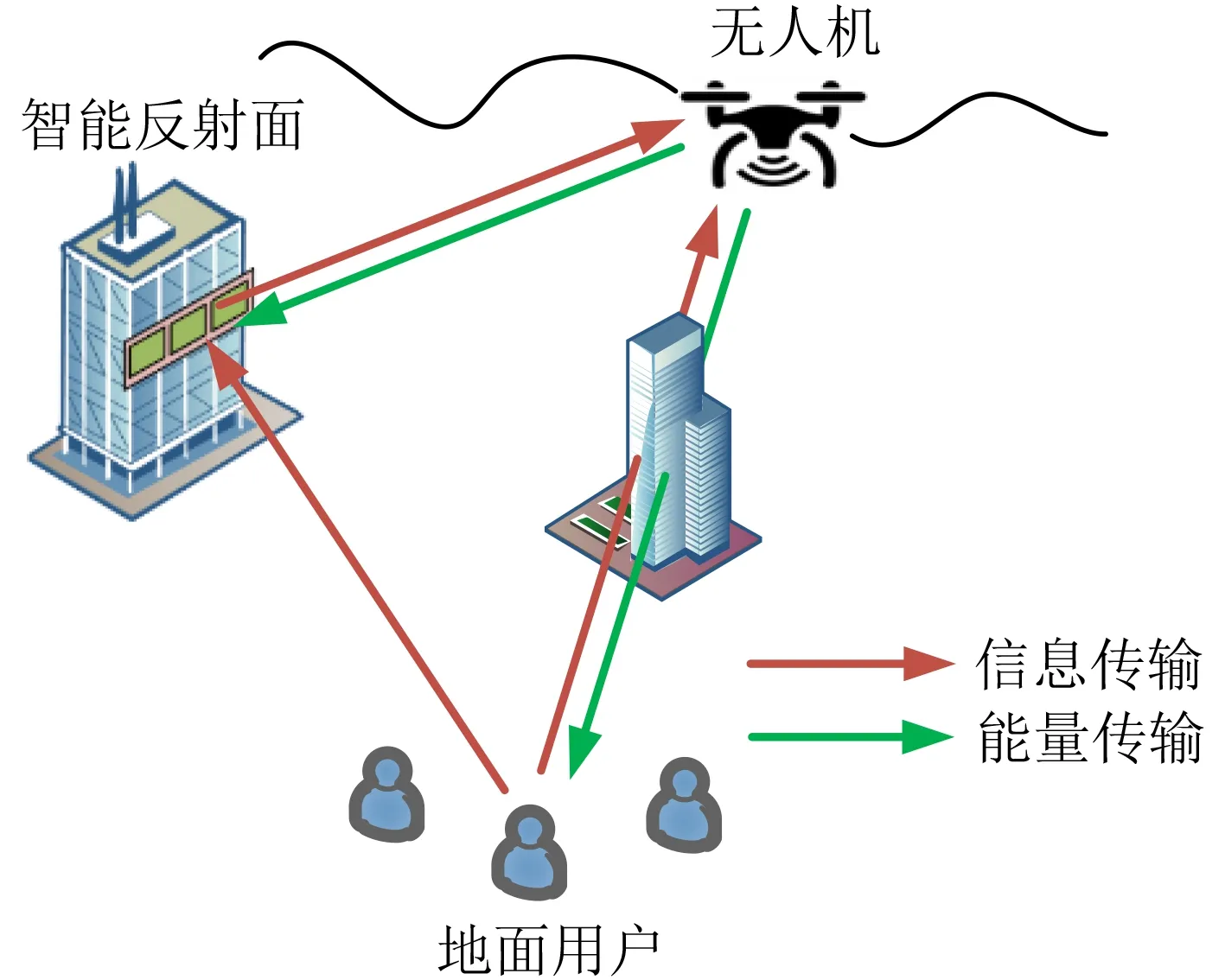
圖1 IRS輔助的UAV供能通信網絡

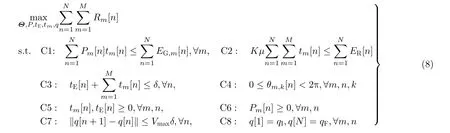
C7和C8表示UAV移動約束。由于目標函數與約束中多處存在變量耦合，因此優化問題式(8)難以直接求最優解。

3 優化問題轉換及求解

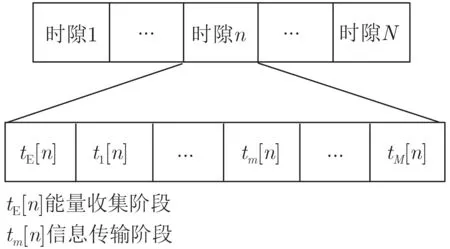
圖2 時隙分配

由于優化問題式(8)存在變量之間的耦合與非凸性，難以用傳統凸優化方式直接求解。為解決這一問題，本文利用BCD資源優化方法，將原問題解耦為3個易于求解的子問題，通過對子問題之間進行交替優化，最終求解原問題。

3.1 IRS相移矩陣優化

首先固定變量P,tE,tm和q，問題式(8)轉變為關于變量Θ的子問題，即

3.2 功率和傳輸時間優化

3.3 UAV飛行軌跡優化

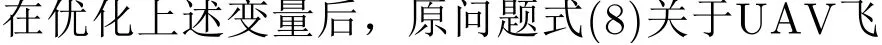
此時由于具有線性的目標函數與仿射約束，子問題式(20)是一個凸優化問題，可利用標準凸優化求解工具CVX求解。為了保證問題式(20)對子問題式(14)具有較好的近似效果，此處采用SCA在每次迭代中多次逼近原問題。通過對上述3個子問題進行交替優化直至收斂，可獲得問題式(8)較為精確的次優解。

3.4 算法分析

綜上所述，基于BCD的資源優化算法如表1所示。所提算法的總計算復雜度主要取決于步驟(3)—步驟(5)。其中步驟(3)的計算復雜度為O{KMN}；步驟(4)與步驟(5)利用CVX中的內點法進行求解，因此其計算復雜度分別為O{(MN)3.5}和O{L1(MN)3.5}[14]，其中L1是步驟(5)中SCA過程的逼近次數。綜上，所提算法的總計算復雜度為O{(KMN+(L1+1)(MN)3.5)ln(1/ε)}， 其中ε為收斂精度。接下來，對所提算法的收斂性進行證明。此處將問題式(8)的目標函數值記為ψ，問題式(20)的目標函數記為ψlb，在第l次迭代中可得到如式(21)的關系

表1 基于BCD的資源分配算法

4 數值仿真及分析

,

圖3展示本文所提算法優化后的UAV軌跡。當U-G鏈路為瑞利衰落模型時，飛行時間充足條件下(N=50)，UAV傾向以直線形式抵達IRS和GUs，并在每個IRS和GU上方懸停一定時間。這是因為UAV靠近傳輸節點以減少路徑損耗，同時有利于能量傳輸和信息收集。在飛行時間不足時(N=20)，UAV仍然可以會發揮其移動性盡量靠近IRS以提高傳輸效率。當U-G鏈路為LoS信道模型時，UAV不再傾向靠近IRS。這是因為在U-G鏈路具有較好的信道環境下，UAV從U-G鏈路可獲得比IRS輔助的反射鏈路更多的性能收益。因此，IRS輔助的UAV系統更加適用于U-G鏈路受阻場景下。

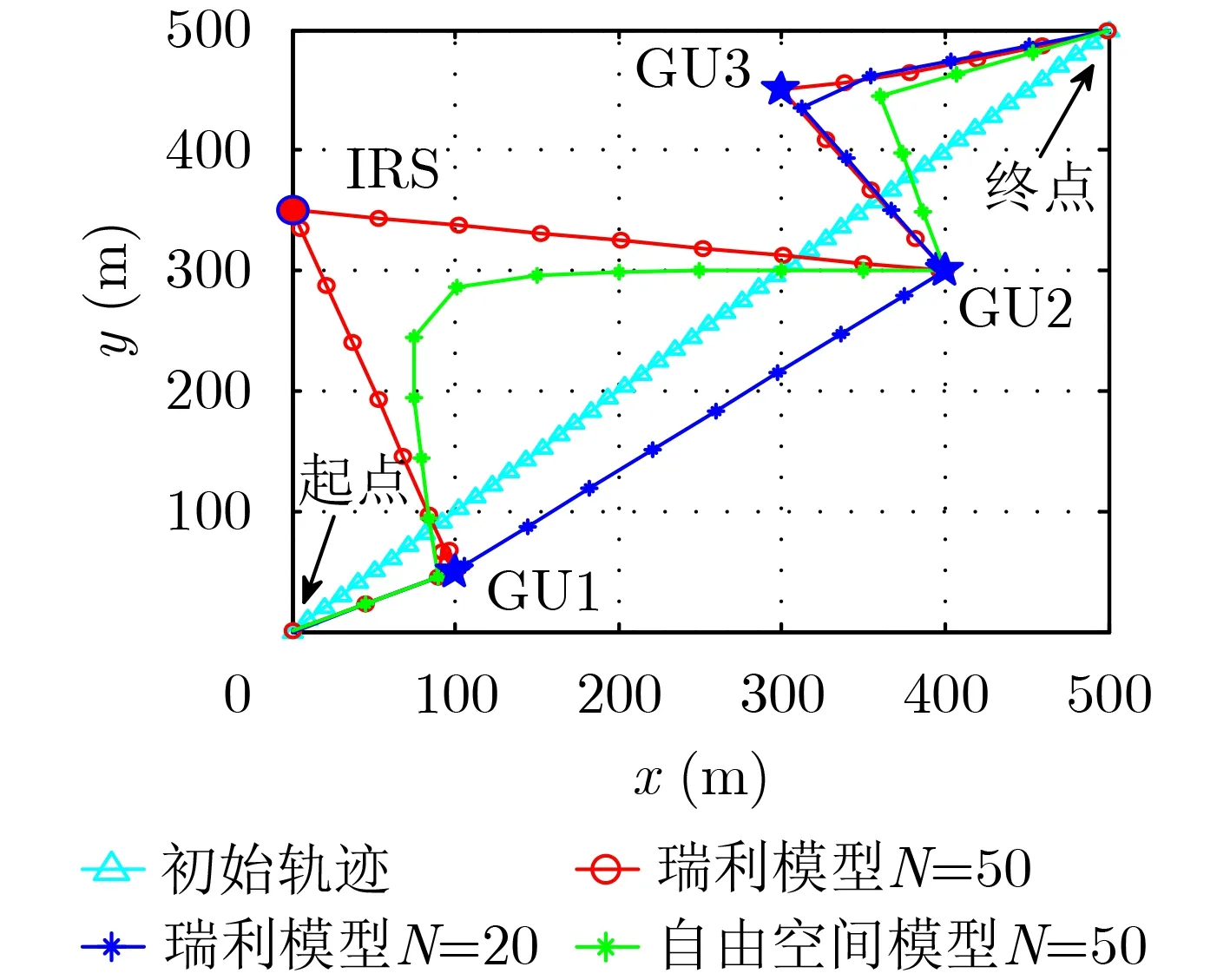
圖3 不同參數下UAV軌跡

圖4給出了不同情況下系統總吞吐量與迭代次數的關系。隨著迭代次數增加，系統總吞吐量升高并最終收斂。由圖可知，所有算法可以在4次迭代后收斂到唯一值，說明所提基于BCD的資源分配算法具有良好的收斂性。

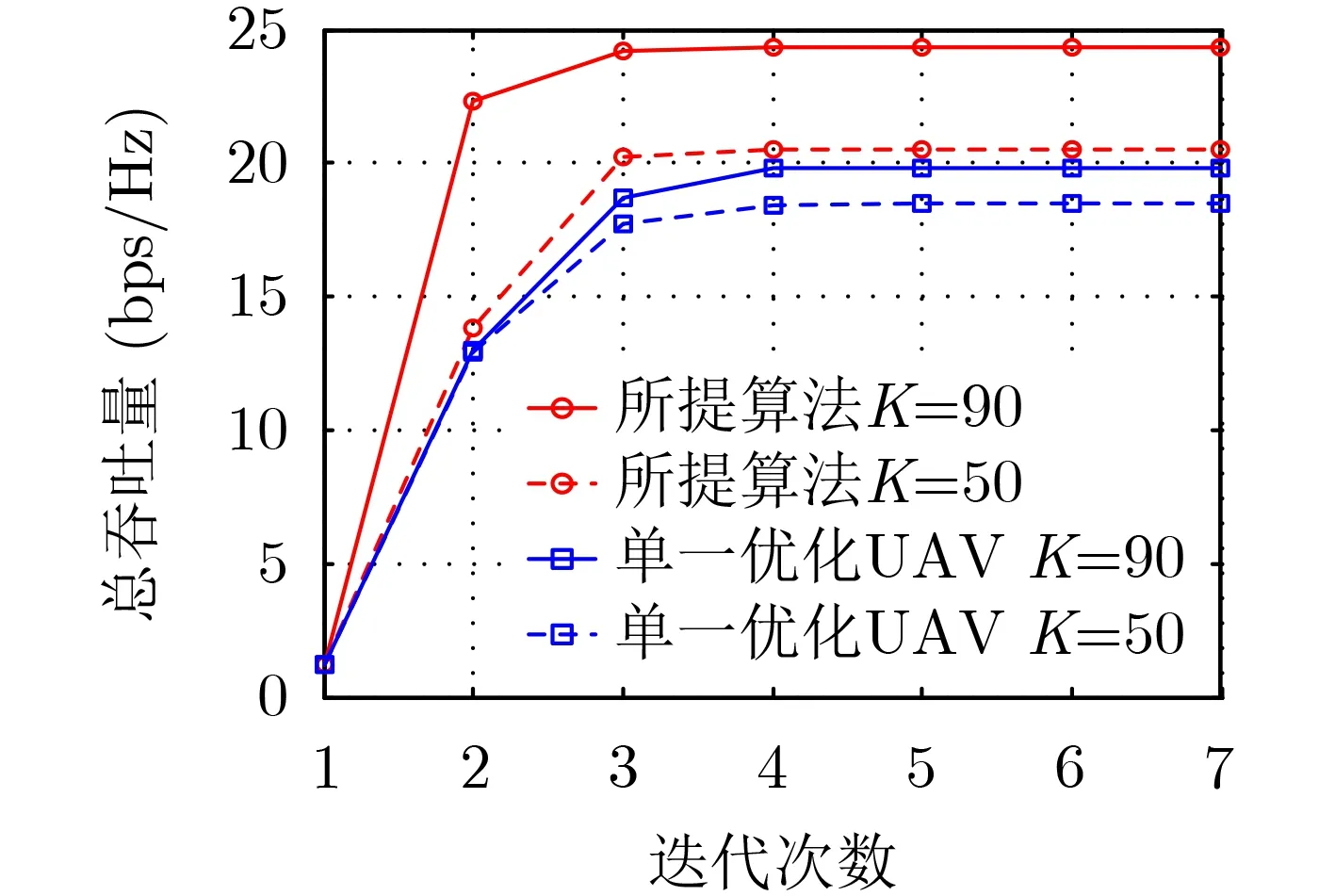
圖4 算法收斂性驗證

圖5給出了使用SCA對原函數的逼近結果。由于1階泰勒展開只能保證近似函數在展開點與原函數相等，而不能保證在整體定義域內對原函數有較好的擬合程度，因此本文采用SCA在每一次迭代中對原子問題式(14)進行多次逼近。如圖5所示，近似值為子問題式(20)最優條件下的目標函數值，將其最優解代入子問題式(14)可得到準確值。可以看到，通過SCA后，近似值與準確值可以保持在很小的誤差范圍，說明1階泰勒展開后的近似函數在通過SCA后，可以很好地逼近原問題，驗證了所提算法的合理性。

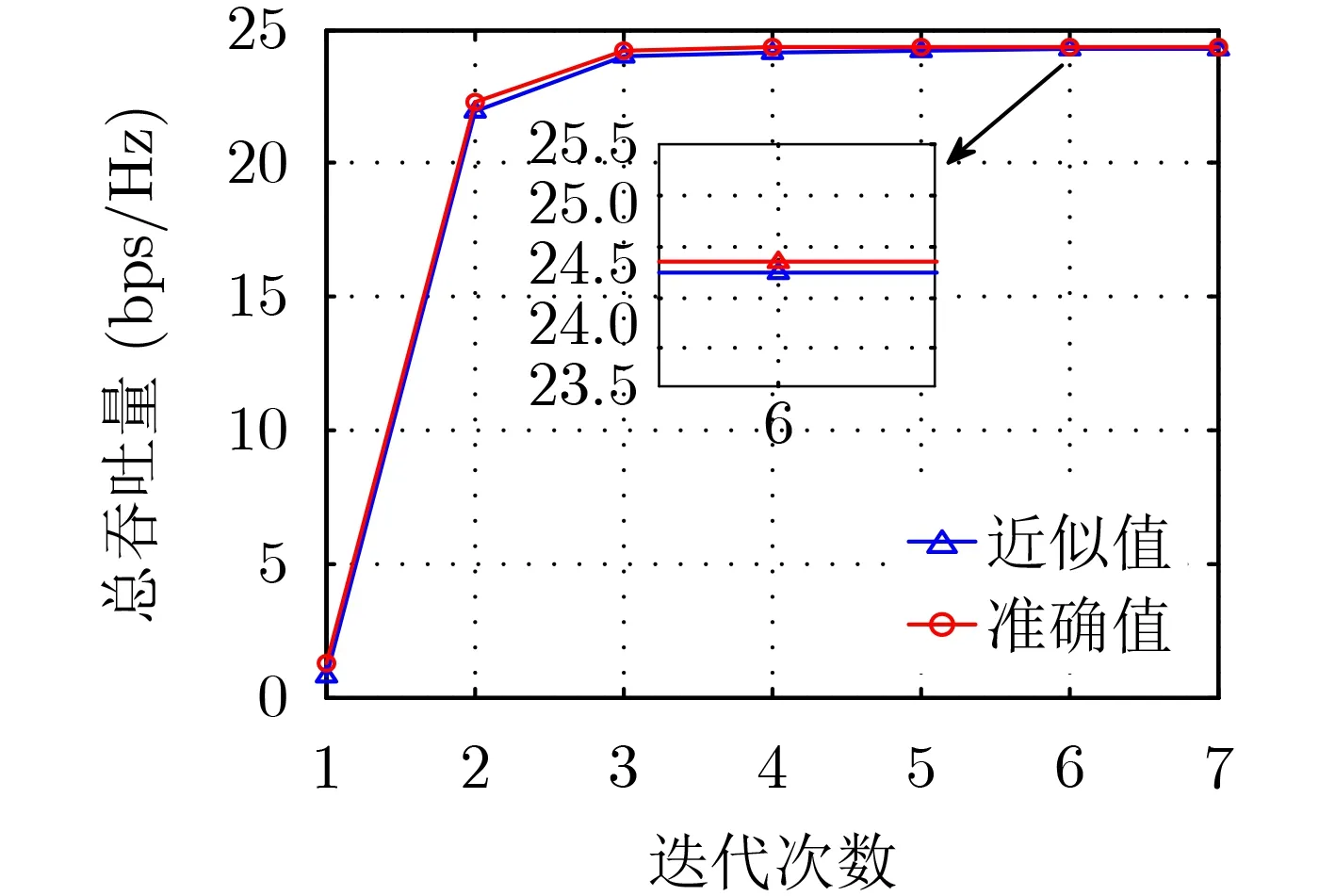
圖5 SCA逼近程度驗證圖

圖6給出了不同算法下，系統總吞吐量與IRS元件數量的關系。隨著IRS元件數量提升，所提算法的總吞吐量提升速度高于單一優化IRS方法實現的總吞吐量。這是因為，單一優化IRS的方法采用初始UAV的飛行軌跡，這導致UAV始終與IRS保持較遠的距離，當UAV信號通過IRS反射至GUs時，會經歷嚴重的路徑損耗。而所提出算法通過發揮UAV移動性，使得UAV靠近IRS與GUs來獲得更好的信道條件，因此其吞吐量隨IRS元件數量提升明顯。同時，單一優化UAV的方法所獲得的總吞吐量和IRS元件數量間沒有明確關系，這是由于隨機優化IRS相移不能保證信號在UAV處對齊合并，甚至相互抵消。綜上所述，與單一優化方法相比，所提出算法通過聯合優化IRS相移與UAV軌跡，可以實現更好的性能。

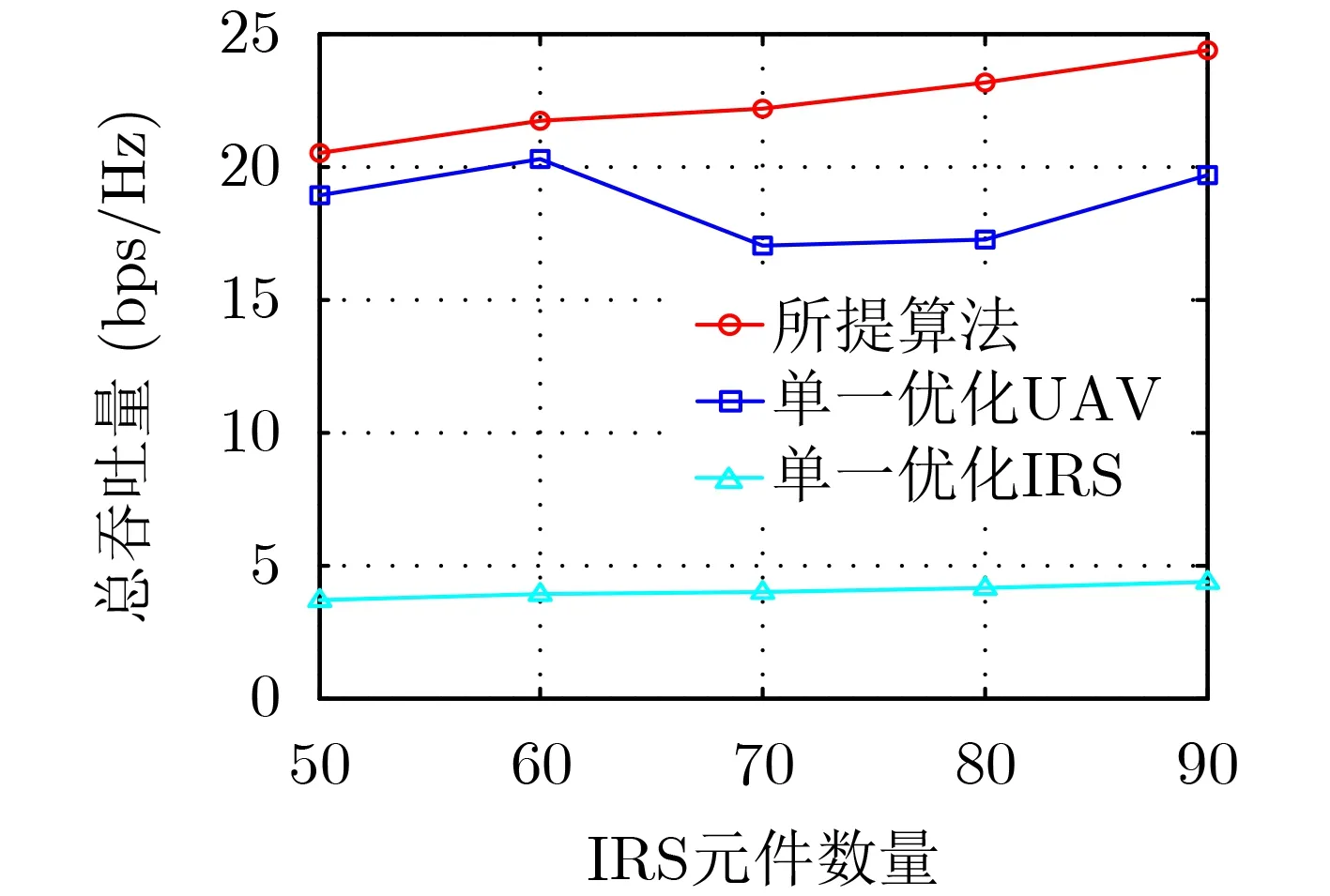
圖6 總吞吐量與IRS元件數量的關系

5 結論

本文研究了IRS輔助的UAV無線供能通信系統下資源分配問題。考慮了IRS和GUs的能量因果、IRS相移和UAV移動性等約束，建立了多變量耦合的系統最大化總吞吐量問題。通過BCD方法將原問題分解為3個易于處理的子問題，并利用三角不等式、引入松弛變量、1階泰勒展開和SCA方法對子問題進行求解。數值仿真表明，所提算法具有良好的收斂性，且可以有效地提高系統總吞吐量。