風電機組傳動鏈振動故障特征提取方法

國家電投集團江蘇新能源有限公司 顧漢富 陳 誠 程 晨

風電機組傳動鏈的旋轉部件容易出現振動故障問題，釋放振動故障信號，這一信號需要通過非線性非平穩動態技術加以識別，如果診斷得當，在早期就能識別了解風電機組傳動鏈旋轉部件故障問題。本文中主要分析了風電機組的傳動鏈部件故障機理與表現特征，分別從迭代數學形態學以變分模態分解兩方面分析風電機組傳動鏈振動故障問題，闡述故障特征提取方法，滿足機組故障診斷與檢查要求。

1 風電機組傳動系統中的故障特征分析

風電機組傳動系統中的故障問題主要存在于軸承和齒輪中。

1.1 風電機組傳動系統中的軸承故障特征

當風電機組傳動系統中主軸處于不同速率運轉階段，其主軸中的支撐軸承都會在時變載荷與重載狀態下承受交變沖擊力作用，此時系統運行安全可靠性就會逐漸降低，出現故障問題。其中比較常見的軸承故障形式就包括了疲勞、腐蝕、磨損、電磨損失效，甚至還會出現變形以及裂縫問題。

在仔細觀察了解軸承故障過程中會發現其內圈、外圈、滾動體以及保持架部分都會出現故障，一旦故障出現，系統滾動體就會通過周期性裝機故障點產生脈沖沖擊信號，參考故障位置不同，其軸承故障特征頻率也會發生變化。如果運用理論計算會發現這一故障與系統的軸承轉速、滾動體個數、接觸角等等因素息息相關。以外圈故障特征頻頻率為例，計算公式應參考如下[1]：f0=frN/2(1-d/Dcosa)。

在上述公式中，fr代表了軸承旋轉率，N代表了滾動體個數，D代表了軸承節徑，d代表了滾動體直徑；a代表了接觸角。軸承振動故障發生的主要原因是軸承運行過程中產生了滾動體與軸承內外圈之間的相互激勵作用。而像軸承過分粗糙、存在表面波紋、軸承安裝過程發生傾斜亦或是主軸彎曲等等問題也會造成軸承振動故障問題發生。故障點在受到周期性撞擊時也會產生激勵作用，進而引發軸承部分劇烈振動。

1.2 風電機組傳動系統中的齒輪故障特征

在風電機組傳動系統中也會出現齒輪故障問題，它是在受交變應力及摩擦力瞬時沖擊作用與影響所產生的，即導致齒輪表面出現各種不同程度的損傷與變形問題。一般來說，系統中比較常見的齒輪故障形式就包括了疲勞點蝕、齒面磨損、膠合以及斷齒。以疲勞點蝕為例，它指代齒輪間在嚙合過程中出現齒輪表面及根部的周期性時變載荷作用，而其內部也會形成交變應力，當這種交變應力一旦超過齒輪材料疲勞極限范圍時，齒輪表面就會出現明顯的金屬剝落現象。而在齒輪齒面接觸點發生相對滾動與相對滑動時，其齒輪齒面的接觸壓力也會發生變化，進一步導致齒輪表面“坑狀”點蝕故障呈現，形成大面積區域金屬剝落，齒輪斷裂故障就此產生。

齒輪發生故障頻率很高，這主要與它的嚙合頻率fm有關，其具體的計算公式應參考如下[2]：fm=n1/60Z1=n2/60Z2，在上述算式中，n1、n2分別代表了主、從動輪轉速，Z1、Z2分別代表了主、從動輪齒數。在發生定輪故障過程中就需要診斷其嚙合頻率，從兩側邊頻帶的頻率內容進行有針對性判斷，發現齒輪之間可能發生的重復性相互沖擊作用，為故障診斷提供重要參考依據。從生產操作過程中看，齒輪發生振動故障的主要原因就是在制造生產過程中產生了誤差，比較常見的是齒輪距偏差，即齒輪質量偏心或者齒形誤差問題，當然潤滑系統表現不佳也會導致齒輪振動問題出現。

2 風電機組傳動系統故障特征提取方法的研究

針對上述所提及的風電機組傳動系統故障問題，下文主要圍繞軸承故障與齒輪故障進行針對性提取，深度研究其故障特征的有效提取方法。

2.1 基于迭代數學形態學的軸承故障特征提取方法研究

2.1.1 迭代數學形態學的基本特征

迭代數學形態學中主要利用結構元素形狀展開分析，例如它會為軸承選擇扁平型結構，基于這一結構元素高度為0的特征確定故障參數。當迭代形態學要求結構尺寸越小時，其所保留的信號特征就越好。在只考慮長度因素條件下，需要基于最小長度中的多個采樣點對結構元素構造進行分析，并建立數據集合即（0 0 0）。在這一數據集合中，要基于傳統形態學中的結構元素定義來分析迭代形態濾波特點，分析結構元素定義內容，確保在單位長度內調整結構元素尺度大小，最大限度保留原始信號特征信息內容，如此對于簡化形態應用操作性有好處，全面提升形態學特征提取能力。

2.1.2 軸承故障的多尺度迭代數學形態學故障特征提取方法

在多尺度形態下，應該合理利用迭代數學形態學內容對擁有不同尺度結構元素的信號系統信號內容進行分析，專門對信號具有良好分析解釋能力的軸承展開有效調整，影響多尺度形態分析濾波效果，形成多尺度迭代形態濾波技術方法。在軸承故障特征提取過程中，可采用自適宜性多尺度迭代形態濾波算法，分析普通多尺度形態背景下的濾波變化情況，并提取其中的迭代數學形態濾波數據內容。這一部分濾波數據內容對于抑制軸承故障特征具有利好，一旦迭代次數達到理想值以后，就會繼續迭代，表現出軸承故障數量遞減趨勢。在迭代過程中，由于自適應情況導致不同尺度下的迭代次數增加，進而達到了最佳的故障提取效果，然后重構系統信號即可，如圖1[3]。

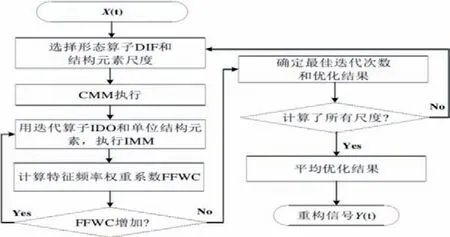
圖1 基于多尺度迭代形態下的濾波流程示意圖

下文結合一實例來談，進一步了解風電機組傳動鏈軸承的故障特征提取方法。

某風電機組傳動鏈軸承存在故障問題，采用兩個不同的傳感器采集振動信號并進行分析，在實驗過程中設置采樣頻率為12kHz，采樣時間控制在1s，將軸承外圈與內圈故障點設置于驅動端，其故障點直徑控制在0.1887mm，負載轉軸速為2000rpm。這里通過計算可以了解到傳動鏈軸承外圈故障特征頻率 =105.4Hz與內圈故障特征頻率 =168.2Hz。

結合上述數據情況，對軸承外圈故障特征進行提取，具體操作如下：首先處理軸承外圈故障內容，安裝驅動端振動傳感器并提取其中信號。考慮到某風電機組傳動鏈傳感器與故障點設置距離相對偏近，因此其振動信號沖擊特性表現非常強，故障特征容易被提取出來。而故障信號在經過CMM處理以后，還需要對信號中的短時傅里葉變換故障特征進行提取，并重構信號，基于多個頻率切片對外圈特征頻率與諧波分量進行分析，了解驅動端振動信號中的高信噪比情況，利用普通多尺度方法有效去除噪聲，發現其中故障特征表現十分明顯。在對頻率切片個數進行觀察計算過程中，發現軸承外圈存在4個頻率切片，其故障特征頻率 中應該包含至少3個諧波，此時應該采用迭代形態方法繼續處理故障問題，基于所有尺度下展開多達60次迭代計算過程，并重構信號，清晰顯示頻率切片的頻率信號情況。

上述結果就表明一點，在強噪聲環境下基于多尺度形態學對軸承故障信號進行分析，其濾波能力比較閑較差，殘余噪聲較多，如果進行優化后平均迭代次數在4次以上。而迭代次數與噪聲強度相關，當噪聲強度越強時，迭代次數也就越大，反之。所以在強噪音背景環境中，可采用上述方法提取軸承故障信號，特征提取效果表現良好[4]。

就整體而言，風電機組傳動鏈系統結構是相當復雜的，其工況條件動態時變性相當強，這就導致傳動鏈內部出現了傳動件故障問題，例如軸承故障。軸承故障往往表現為特征微弱、不易于被識別和診斷，針對這一問題才提出了迭代數學形態學概念，基于此構建濾波技術體系，基于普通單尺度與多尺度形態上展開濾波操作，構造形成兩個或兩個以上的優化算法，主要用于對電動機軸承與風電機組傳動支撐軸承故障進行診斷分析，并獲得相應診斷結論。就目前的自適應多尺度迭代形態濾波方法可以有效解決多尺度形態背景下的濾波問題，基于小尺度結構元素對欠濾波問題進行分析，提高故障特征提取過程自適應性。特別是要在強噪聲環境下對故障特征表現進行分析，以此獲得頗為理想的故障特征提取效果。

2.2 基于變分模態分解的齒輪故障特征提取方法研究

2.2.1 變分模態分解的基本特征

基于風電機組傳動系統中傳動鏈的趨勢濾波發生情況，需要結合相關算法簡化信號參數，改進傳動系統的整體自適應性與安全可靠性，由此就提出了具有試探屬性的變分模態分解算法，通過動態時間規整處理模式混疊問題，對傳動系統中的齒輪故障時域與頻譜特征進行全面提取分析，獲得提取結果，證明這一結果是具有有效性與安全可靠性。

2.2.2 齒輪故障的變分模態分解故障特征提取方法

基于變分模態分解方法，要對齒輪故障特征進行提取，從最初的原始信號頻譜結構中原始信號簡化出發思考問題，直接定義方法內容，從信號分解過程中的變化過程來建立自適應定義分析機制。在結合機械故障診斷領域中的信號參數自適應定義方法缺點分析計算效率相對較低問題，同時對齒輪故障所缺乏的可靠性與健壯性問題進行深度分析，在其過程中也要注意特征信息遺失問題，深度考慮指標對比結果后所表現出的正向效應結果。

而為了提升計算效率，需在計算前后對多個指標的差與預設閾值進行進一步對比，分析結果正向效應，在利用變分模態分解方法過程中建立自適應定義，分析其中的弱可靠性問題，建立試探性變模態分解模型，最大限度減少模式混疊問題。最終，還要利用動態時間調整信號重構方法，結合仿真信號與風電機組齒輪箱故障信號分析表明相應方法，進一步診斷齒輪故障，對齒輪故障中的自適應性與安全可靠性內容進行調整[5]。

在針對齒輪故障的動態時間規整處理過程中，需要對現實信號中的復雜性問題進行分析，基于分解過程了解最終分析結果，實現信號重建過程。在這一過程中，要有效解決模式混疊問題，基于動態時間規整對信號進行重構，同時建立并評估不同時間序列，提出相似性故障提取方法。在故障提取環節，需要圍繞齒輪故障的連續性約束與單調性兩點進行分析，確保序列之間的最佳匹配定義為兩個序列，同時找到所有規劃路徑中的最小累積距離規劃路徑，結合動態時間規整機制分析故障提取特征問題，例如要對不同時間序列長度進行分析，同時對不同實驗參數應用序列采集過程健壯性進行分析。

考慮到風電機組傳動系統中傳動鏈的機械故障沖擊信號表現相對敏感，所以要在變分模態分解故障過程中了解特征信息量評價指標，對相關算法參數進行設置，始終保證信號保真約束平衡滿足參數設置要求，避免信號丟失現象出現。

3 結語

本文中研究了風電機組傳動系統傳動鏈中軸承與齒輪部件的故障問題，在分析故障問題之余運用迭代數學形態學以及變分模態分解兩種方法計算提取故障特征，希望借此機會對系統中所出現的早期故障進行診斷識別，結合理論基礎之上深入分析診斷故障，并取得了一些頗有價值的創新性成果。上述兩種故障提取方法都是區別于傳統方法的，在計算方法方面有所創新，具有連續性特征。例如在充分考慮到迭代學中的自我優化特征與強去噪能力，在經過較少次數迭代后就能輕松將故障特征提取出來，這對于結構元素定義相對復雜的風電機組傳動系統傳動鏈軸承故障檢查是十分有利的。