基于響應面法的高精度齒輪成型工藝設計及優化

0 引 言

隨著聚合物制造工藝技術的發展，塑料齒輪在市場中的份額逐漸增加。與金屬齒輪相比，塑料齒輪具有質量輕、制造成本低、自潤滑性能好、吸收沖擊和振動能力強等優點，因此被廣泛應用于汽車、航空航天、醫療等領域

。增材制造是塑料齒輪制造的重大突破，但主要用于小批量生產

。目前，塑料齒輪主要采用注射成型的方法生產，但對于小模數塑料齒輪（模數≤1mm），在微注射成型中仍存在較多問題

，其中最大問題是尺寸精度不足。由于聚合物的固有收縮，待成型齒輪在保壓冷卻階段會發生非線性收縮，在冷卻階段由于溫度分布不均勻會產生殘余應力，導致最終成型齒輪與模具型腔幾何形狀產生偏差，影響齒輪傳動的穩定性，產生振動和噪聲，縮短小模數塑料齒輪的使用壽命

。

該類研究主要是日本移民美國和拉美地區的相關研究。日本移民美國的研究集中在政策演變過程研究、史學研究、國際關系研究，在時間序列上學者主要研究了19世紀末20世紀初這段時間美國的日裔移民問題以及這一時期美中日三國的國際關系；日本移民拉美地區的研究則關注日本移民對拉美地區的社會結構和農業生產造成的影響研究，日本移民的文化認同和融合研究等。

BBD（box-benhnken design）是一種常用的響應面設計方法，通過對主要影響因素進行試驗，回歸擬合全局范圍內各因素與目標間的函數關系，可獲得精度高、預測性好的非線性數學模型，從而分析各因素對試驗結果的影響規律

。現通過Design-Expert12軟件，采用BBD響應面法設計試驗并對結果進行分析，研究注射工藝參數及其交互作用對翹曲變形的影響規律

。

針對某汽車尾門驅動器的行星齒輪，設計了注射成型工藝，借助Moldflow有限元軟件對其成型過程進行模擬分析，通過響應面法探究工藝參數對塑件成型質量的影響，并在此基礎上開展成型試驗驗證，制備了合格的行星齒輪。

1 注射工藝優化設計

1.1 有限元模型建立

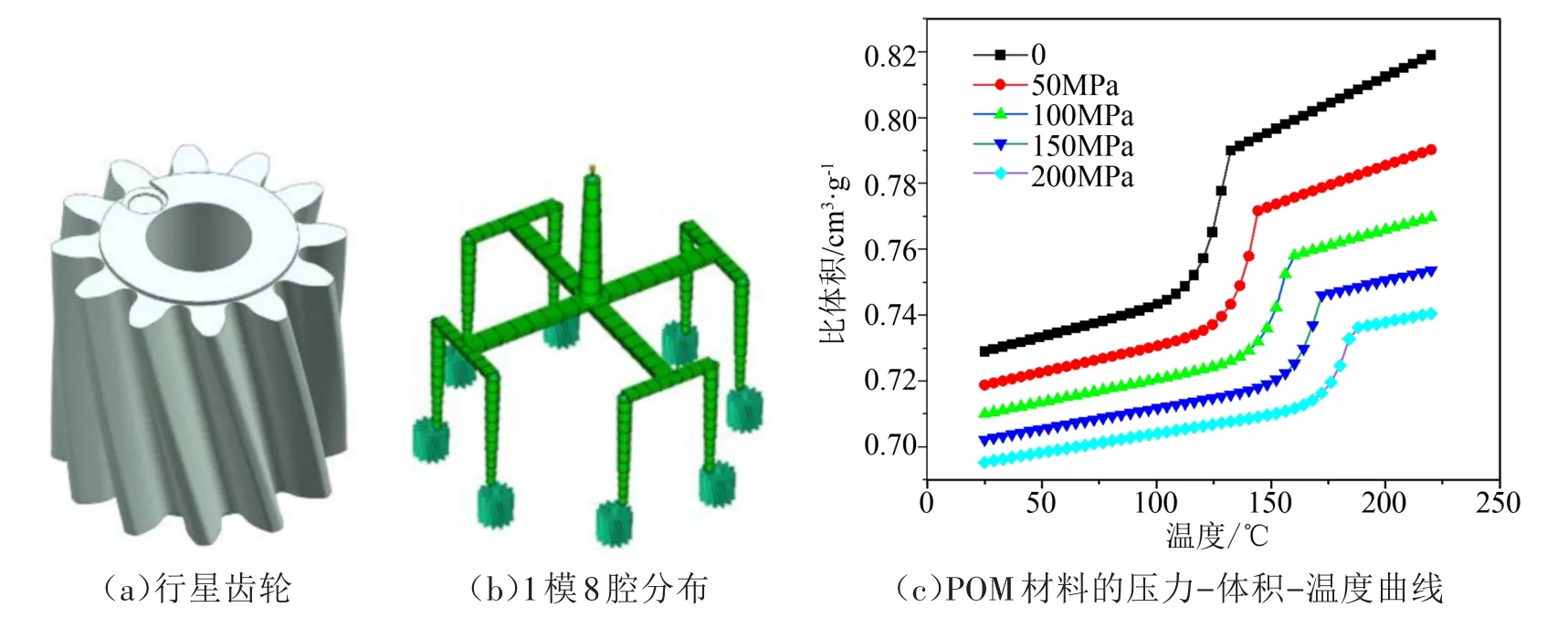
圖1（a）所示為汽車尾門驅動器中的行星齒輪，采用NX12.0建立齒輪模型，主要幾何參數如表1所示。將模型導入Autodesk Moldflow Insight中進行流道澆口設計、網格劃分以及冷卻系統的建立。選擇“Cool+Fill+Pack+Warp”工藝方案進行數值模擬，以小齒輪的翹曲變形量為研究對象建立有限元模型。

根據本工程實際條件，借助易工軟件對沉箱基礎結構受力以及抗滑、抗傾覆情況進行計算，計算結果見表1。分析可知：

為了提高生產效率，模具采用1模8腔布局

，如圖1（b）所示。澆注系統采用平衡式進料，以保證熔體能快速平穩填充型腔。根據性能要求，塑件材料選用POM（聚甲醛），該材料的相關性能參數如圖1（c）所示，根據其物理與化學特性選擇推薦工藝參數，如表2所示。

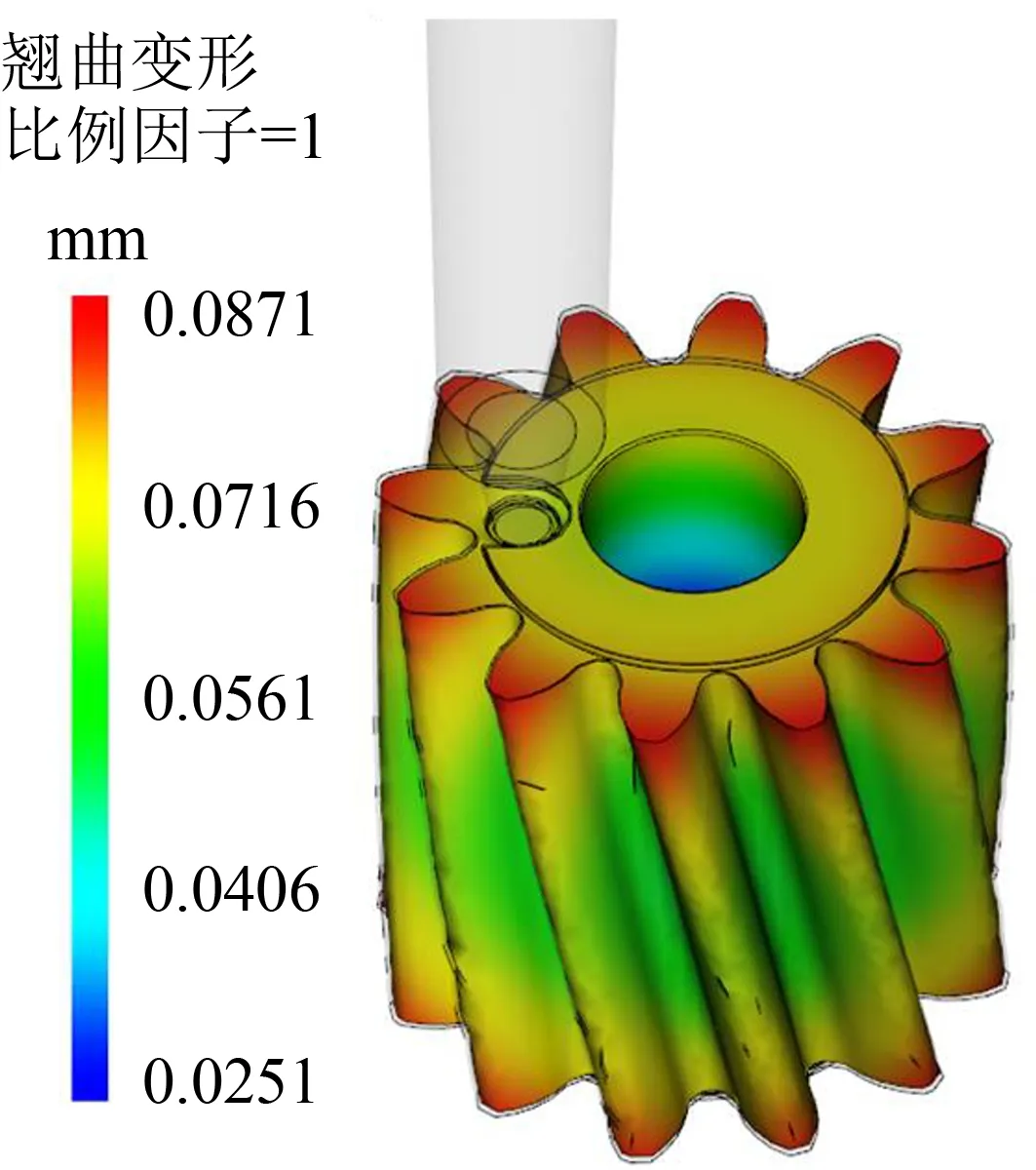
1.2 數值模擬結果

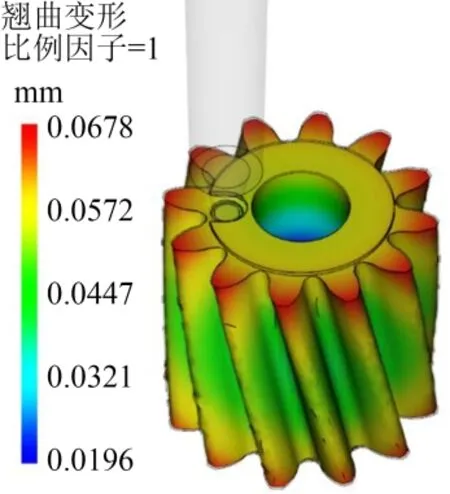
推薦工藝參數的數值模擬結果如圖2所示，其中黑色輪廓線為材料收縮前理想的輪廓，齒輪在冷卻過程中產生收縮導致翹曲變形。從圖2可以看出，在齒輪上、下表面的輪齒部分變形最嚴重，翹曲變形為0.087 1 mm，而中間部分變形較小。這是因為在各種外界因素的作用下，熔融材料分子鏈的無序和弛豫被破壞，使熔體處于不穩定狀態，產生不均勻的殘余應力；而在分子鏈松弛或再結晶過程中，應力會被釋放，相應部位會收縮，導致翹曲變形

。

1.3 工藝參數耦合優化設計

采用BBD中心組合進行試驗，運用Design-Ex?pert12軟件設計方案，選擇對翹曲變形具有影響的4個因素：熔體溫度

、模具溫度

、保壓壓力

和保壓時間

，進行4因素1水平的響應面分析，以翹曲變形量(

)為響應目標

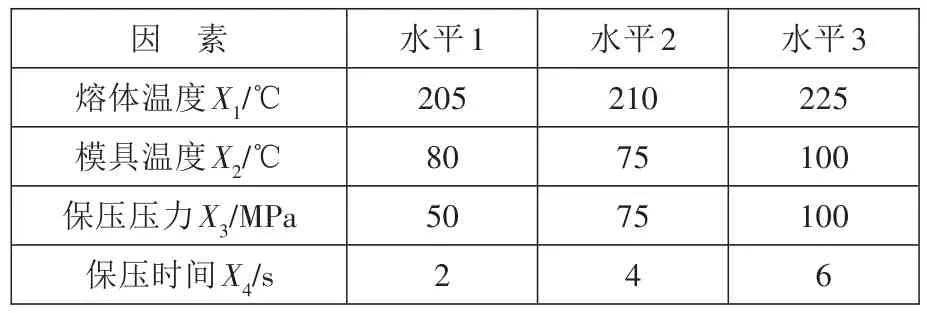
。各試驗因素水平表如表3所示，水平1、2、3分別對應低值、中間值和高值，冷卻液溫度均為25℃。

試驗模型采用二次回歸線擬合，公式如下：

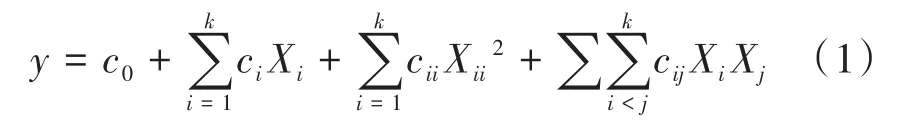
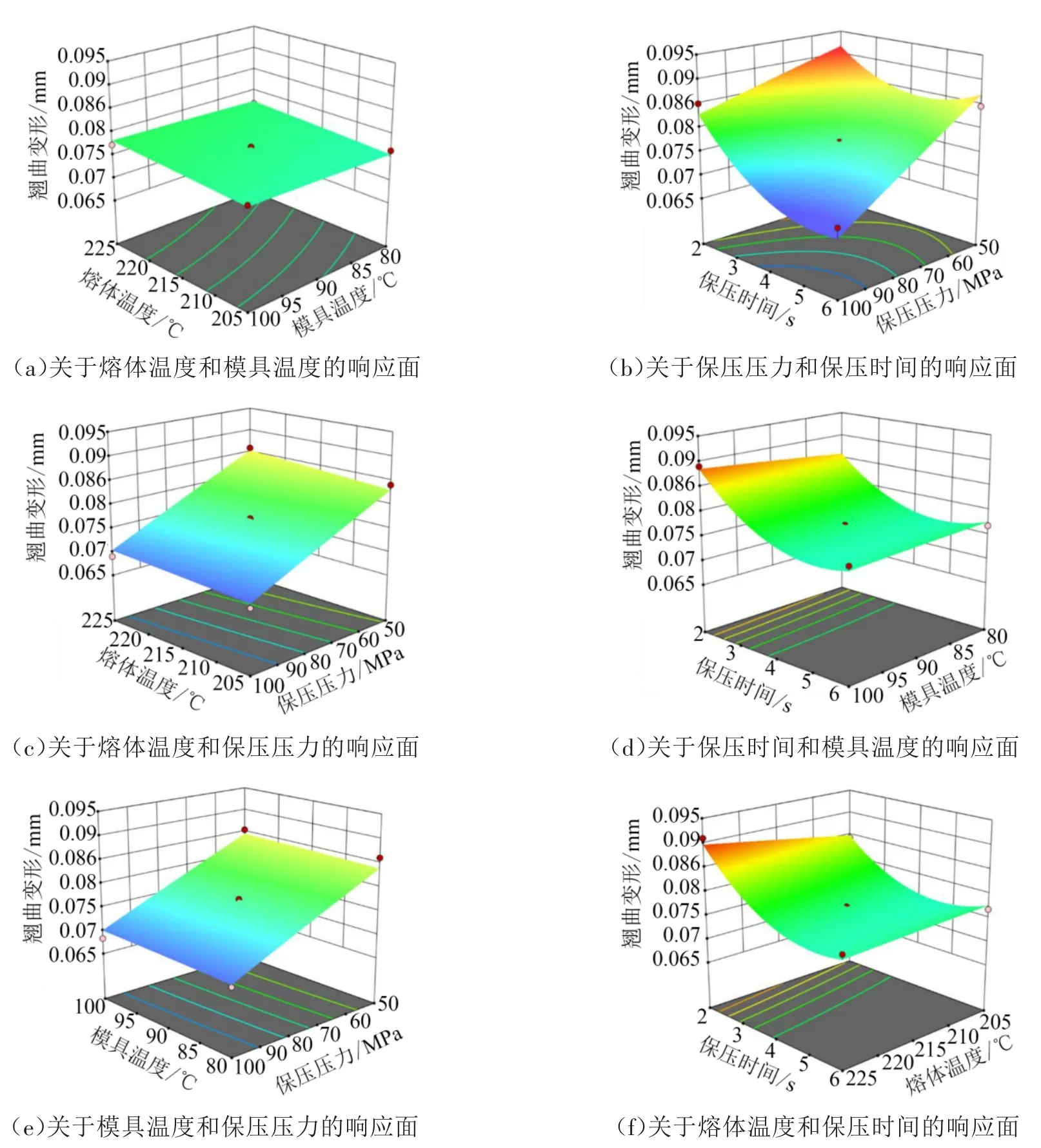
圖4所示為翹曲變形關于不同設計變量的響應面。從圖4（a）可以看出，翹曲變形隨著熔體溫度與模具溫度的升高而增大，但增大的效果不明顯。由圖4（b）～（d）可以對比發現，保壓壓力和保壓時間對翹曲變形的影響較大，當保壓時間一定時，翹曲變形隨著保壓壓力的增大，呈現先減小后增大的趨勢，且隨著保壓時間的增大，極小值呈現向左移動的趨勢。根據方差分析可以得出最優注射成型工藝參數：模具溫度為87.229℃，熔體溫度為217.613℃，保壓壓力為98.528 MPa，保壓時間為5.595 s。將最優工藝參數組合輸入到Moldflow軟件中進行分析，得到的翹曲變形為0.067 8 mm，模流分析結果如圖5所示。

1.4 響應面模型建立

由表6可知，響應面預測的響應值與有限元分析驗證的響應值近似，誤差率僅為1.18%，擬合精度為98.82%，具有較高的接近度，故建立的響應面模型具有較高的預測精度。驗證結果表明所構建的響應面模型可靠，驗證的最優工藝方案的翹曲變形相較于推薦工藝方案的翹曲變形降低了22.16%。因此，該方法能較準確和高效地預測不同工藝條件下的齒輪成型質量、縮短分析周期和提高生產效率，降低反復試驗或分析帶來的成本。

1.5 響應面模型驗證

模具為1模8腔三板模結構，如圖6所示。旋轉型芯13和螺旋齒套15的導程與齒型鑲件18相同，推出時由螺旋齒套15對旋轉型芯13施加旋轉力矩，使旋轉型芯13帶動塑料齒輪同步旋轉，避免齒型在脫模時受到齒型鑲件的扭力而導致齒型變形的情況。

通過

值判斷對象的顯著性、

值判斷對象被拒絕的概率，由均方差判斷影響因子對于響應面模型的影響程度，均方差越大，表明對響應的影響越顯著。失擬項用以評估擬合方程的可靠性，利用復相關系數

2、修正的復相關系數

2

、預測的復相關系數

2

統計估計量評價響應面模型的有效性，信噪比

的信號值大于4才能用于模擬

。

值越大表明模型擬合度越高，

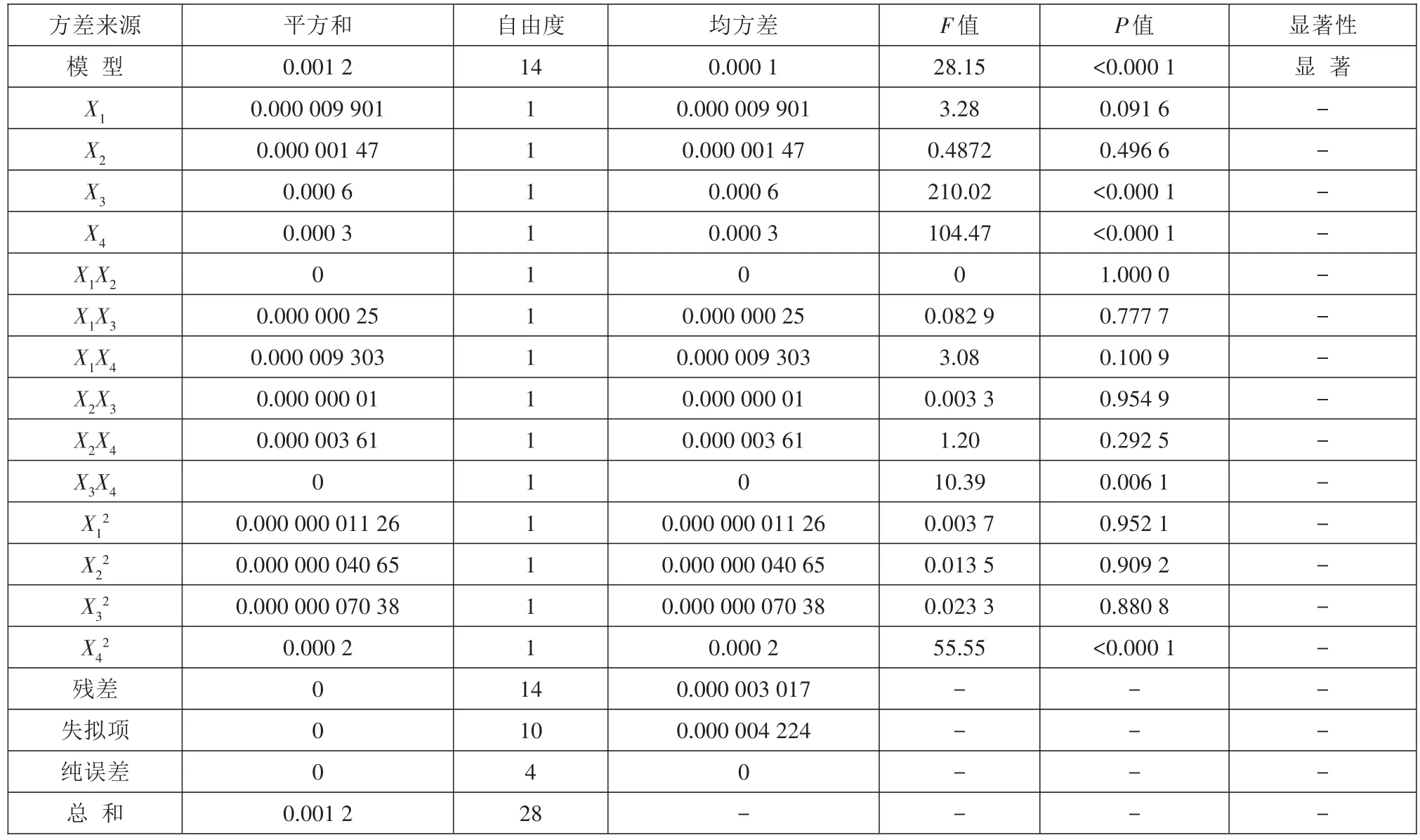
值小于0.05表明模型顯著。根據表5可知，最小翹曲變形的模型

值為28.15，且

值均小于0.000 1，說明該響應面模型均具有顯著性；最小翹曲變形的

2為 0.965 7、

2

為 0.931 4，表示該模型的

2與

2

吻合較好，模型的相關性較好，因此最小翹曲變形的響應面模型（回歸方程）有效。此外，

2

與

2

在最小翹曲變形上也有較好的一致性，說明模型合適。最小翹曲變形的響應模型的信噪比

為19.839，表明模型具有足夠的分辨能力。

3.沿著虛線裁下評刊表，郵寄到：浙江省杭州市下城區西湖文化廣場32號樓6樓633室《幽默大師·漫話國學》編輯部（郵編：310006）。（還可以附上來信，寫上你想對小編說的話、對雜志的建議、想看的其他國學知識等等，小編都會一一回信并贈送小禮品哦！）

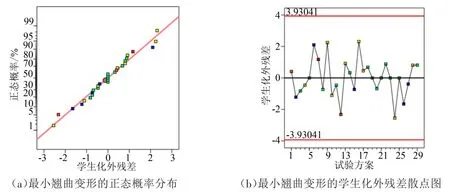
正態概率與學生化外殘差關系如圖3所示，散點分布在直線上或均勻分布在直線兩側，該模型擬合程度較好，可信度較高。

2 優化結果及分析

模具溫度控制在80～100℃，熔體溫度控制在205～225℃，保壓壓力設置為50～100 MPa，保壓時間設置為2～6 s。經過迭代，獲取全域范圍的數值，得出最優注射成型工藝參數，對比BBD得到的29個樣本工藝參數分析結果，響應面模型優化得到的塑件翹曲變形更小

，即該收縮率更小，品質更佳。

其中，

為響應平均值；

c

為線性系數；

c

為二次回歸系數；

c

為交互回歸系數；

X

和

X

為設計變量；

為響應值；

為設計變量個數；

、

c

、

c

、

c

通過逐步回歸方法獲取。

BBD試驗設計及結果如表4所示，采用Design-Expert12軟件根據式（1）對試驗數據進行二次回歸分析，獲得翹曲變形的非線性二次回歸模型，對試驗數據進行精確的統計分析，提供具有連續性特征的圖像分析，直觀地表征研究因素與響應目標之間的對應關系

，如式（2）所示。

3 試驗與討論

3.1 模具設計

由于行星齒輪具有一定的螺旋角，注射完成后脫模難度大，常用的脫模方法有齒型鑲件旋轉和齒輪制品旋轉2種方式

。該塑料行星齒輪精度要求高，需求量大，對其模具要求較高。齒輪分度圓螺旋角

=12.5°，直接推出會導致齒面受力過大而變形，引起齒型精度超差，需要設計同步脫模機構。該模具設計了一種型腔錯位推出結構，利用同步脫模結構的軸向間隙，在旋轉型芯復位的過程中讓齒圈與制品產生錯位將成型制品推出，解決了制品推出的問題。

近年來，快遞行業隨著電商的發展而壯大，其市場競爭也日趨激烈，許多快遞企業都面臨著轉型的問題。與此同時，即時配送伴隨O2O經濟和“懶人經濟”迅速興起，具備著極大的市場發展潛力。因此，某些面臨轉型的快遞企業為了盡快搶占即時配送的市場份額，從而迅速開拓了這一新的業務領域。因即時配送具有即時性、短距離、高頻次等特點，較之傳統快遞還有著很大的區別。所以，某些快遞企業雖然組建了自己的專職配送團隊，卻因缺乏相關的經驗，造成其面臨著很多問題：運力投入不合理、配送路線雜亂、難以保證服務時效、配送成本居高不下等問題。

針對該模型進行最小翹曲變形回歸方程的方差分析和顯著性檢驗，結果如表5所示。

值表示原假設被拒絕的概率，

值表示模型的可靠性與因素的顯著性，

值與

值之間通過一定的統計學原理相關聯。

值越小、

值越大表示二次回歸模型越可靠

。

本文主要研究智力資本、戰略柔性對中小企業技術創新能力的影響。從目前的研究文獻來看，針對中小資企業技術創新能力的研究主要集中在創新過程中存在的問題及原因方面，很少有研究從微觀層面對中小企業技術創新能力的影響因素進行分析。本文按照相關學者的觀點對智力資本和戰略柔性這兩個因素進行維度的劃分，并分別研究它們對技術創新能力的影響。本文首先對研究要素進行概念的界定，然后提出研究假設，最后進行結果分析。

以“95后”為主體的當代大學生群體，生活在一個“大眾創業，萬眾創新”的競爭時代，而且這種競爭是全球性的，在這種現實下，他們能夠很清晰地看到這個社會所需要的能力，也意識到多一份技能將更有利于自己將來的競爭，因此對于學校提供的服務不再限于專業學術性知識的傳授，轉而希望獲得一種綜合能力，如圖2所示，包括人文素養、人際交往能力、國際視野、組織領導能力等。

齒輪推出時，由于型芯和螺旋齒套中間設計有2.5 mm的軸向間隙，塑料齒輪從齒型鑲件18推出后，型芯回退而齒型鑲件18不動，使塑料齒輪和齒型鑲件18的牙型出現相位差，使齒型鑲件18將塑料齒輪從旋轉型芯13上推出。這種脫模方式避免了旋轉脫模時齒面受到的旋轉扭力，保證了塑料齒輪的齒型精度。

3.2 檢測與結果對比

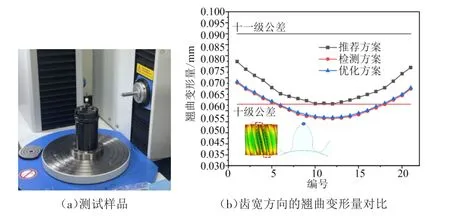
在模具設計制造完成后，采用注塑機對行星齒輪進行試制，得到的樣件如圖7所示。從圖7可知，采用最優工藝參數所生產的行星齒輪整體順滑無瑕疵，外觀良好無飛邊，壁厚均勻，斜齒規整。

通過檢測儀對試制樣品進行相應的注射精度檢測，從行星齒輪的齒寬方向依次選取21個齒頂點，如圖8所示，齒輪兩側的翹曲變形量較之中間部分大，齒寬方向呈現鼓形狀，與檢測結果的輪廓曲線相似；優化方案的翹曲變形量相較于推薦方案減小，表明優化方案具有良好效果；檢測方案的翹曲變形量相較于優化方案略小，趨于吻合。成型的齒輪達到十一級公差，符合工藝要求。

總之，通過在血液與腫瘤疾病OSC橫向整合聯合CBL的教學改革，使血液與腫瘤疾病這門專科性極強的醫學知識更有效地為學生所接受。但在實踐教學過程中仍存在問題，需要進一步完善和探索。

4 結束語

（1）基于BBD響應面法建立的成型工藝參數與翹曲變形之間的二次回歸模型顯著，其擬合精度為98.82%，表明構建的響應面模型可靠。

（2）通過響應面預測的最優工藝參數為：熔體溫度217.613℃、模具溫度87.229℃、保壓壓力98.528 MPa、保壓時間5.595 s。分析注射成型工藝參數對最小翹曲變形的影響規律，得出對翹曲變形影響最大的工藝參數為保壓壓力和保壓時間。

（3）采用模流分析技術與響應面模型技術相結合的方式優化工藝參數，優化后的翹曲變形減少了22.16%。

[1]項麗萍,楊紅菊.基于神經網絡技術的塑料齒輪模型工藝參數優化[J].工程塑料應用,2021,49(5):92-96,107.

[2]趙 建,張勤星.注塑制品的翹曲優化與分析[J].高分子材料科學與工程,2010,26(10):167-170,174.

[3]HE X,WU W.A practical numerical approach to character?izing non-linear shrinkage and optimizing dimensional de?viation of injection-molded small module plastic gears[J].Polymers,2021,13:2092.

[4]鄭 玲,鄧 鑫,焦曉嵐,等.基于正交試驗優化PLA的3D打印工藝參數[J].工程塑料應用,2021,49(10):68-72,80.

[5]石照耀,張萬年,林家春.小模數齒輪測量:現狀與趨勢[J].北京工業大學學報,2008(2):113-119.

[6]吳守軍,馮輔周,吳春志,等.行星輪系動力學分析與響應表示方法研究[J].振動工程學報,2021,34(6):1177-1186.

[7]高 貴,龔 俊,李瑞紅,等.表面織構對PTFE復合材料摩擦磨損行為的影響[J].摩擦學學報,2020,40(6):697-706.

[8]戴亞春,王 勻,周建忠,等.微齒輪注射成型正交優化及數值模擬[J].材料工程,2010(7):46-48,53.

[9]左繼紅,劉麗麗,蔡 頌.基于Moldflow交流接觸器底蓋最佳澆口的研究[J].塑料工業,2021,49(1):85-88.

[10]WANG T H,YOUNG W B.Study on residual stresses of thin-walled injection molding[J].European.Polymer.Jour?nal,2005,41:2511-2517.

[11]劉 強,陳洪榮,梅 端,等.基于正交試驗與BPNN-GA的航標燈外殼注射工藝參數優化[J].塑性工程學報,2020,27(7):123-129.

[12]FENG Y Y,ZHANG H G,LUO Z G,et al.Loading path opti?mization of T tube in hydroforming process using response surface method[J].The International Journal of Advanced Manufacturing Technology,2019,101(58):1979-1995.

[13]王若寒,畢 超,李 翱.基于響應面法的對乙酰氨基酚片劑FDM成型的工藝優化研究[J].中國塑料,2021,35(9):69-74.

[14]張 池.大膨脹率薄壁管脹鐓復合內高壓成型工藝研究[D].南昌:江西理工大學,2021:34-46.

[15]傅建鋼.基于響應面模型的注塑件精密成型工藝優化[J].合成樹脂及塑料,2021,38(2):58-61.

[16]胥樹志,顧來法,徐平均,等.帶金屬螺桿塑料斜齒輪注射模設計[J].模具工業,2021,47(11):60-64.