焊管冷彎回彈曲線方程構建及工藝優化

趙月偉，帥美榮，楚志兵，桂海蓮，趙曉東，高虹，鄔莉華，翟麗麗

塑性成形

焊管冷彎回彈曲線方程構建及工藝優化

趙月偉1，帥美榮1，楚志兵1，桂海蓮1，趙曉東1，高虹2，鄔莉華3，翟麗麗2

（1.太原科技大學 重型機械教育部工程研究中心，太原 030024；2.武進不銹股份有限公司，江蘇 常州 213111；3.中鋼不銹鋼管業科技山西有限公司，太原 030600）

研究316L奧氏體不銹鋼板材JCOE彎曲卸載回彈和應力分布特征，對預彎曲量實施相應補償，以提高彎曲成形精度。基于彈塑性變形理論，利用有限元模擬研究各關鍵成形參數對板材彎曲卸載回彈的影響規律，將影響指標線性/非線性擬合疊加，構建回彈曲線方程。板料回彈量與上模下壓量、下模開口量呈線性關系，與上模下行速度、摩擦因數呈指數關系。優化后的最佳冷彎成形工藝參數如下：上模下壓量為12 mm，下模開口量為150 mm，上模下行速度為4 mm/s，摩擦因數為0.15。對于徑壁比值≤10的板料成形，理論計算得到的彎曲回彈量與實測平均值吻合較好，構建的模型可以為實際生產奠定理論基礎。

焊管冷彎；回彈解析；回彈方程構建；工藝優化

海洋油氣資源開發工程裝備是海洋經濟的先導性產業之一，其蓬勃發展將直接推動各類配套管材制造業的快速發展[1-2]。美國、日本和歐洲油氣輸送管材生產商普遍采用直縫埋弧焊管，其主要生產工藝是UOE和JCOE工藝[3-5]。無論采用哪一種制管工藝，成形路徑都比較長，多次彎曲回彈歷史的累積效應與板坯初始形狀、材料性能參數、模具結構參數以及工藝參數等影響因素有關。因此，確定多種因素及其耦合作用對管坯成形與回彈的影響、提高產品精度是工業生產中迫切需要解決的問題。

Gattmah等[6]研究了鋼板在不同幾何參數下的變形行為，采用雙面漸進成形方法，提高了彎曲過程的幾何誤差。Pourboghrat等[7]根據板料曲率與橫截面彎矩關系，分別利用各向同性強化和線性隨動強化2種方式對板料彎曲回彈量進行計算，結果表明，在有明顯包辛格效應的情況下，線性隨動強化材料模型對回彈預測效果更好。Padghan等[8]根據板料材料特性和幾何參數計算彎曲力，研究了一種人工神經網絡和有限元方法，估算了鋼板彎曲過程中的回彈值。劉克進[9]對凸弧翻邊、凹弧翻邊、V形彎曲和U形彎曲等典型沖壓工藝進行了回彈試驗研究，同時結合遺傳算法，獲得了具體材料和工藝條件下的回彈經驗公式。

近年來國內外學者圍繞耐腐蝕焊管成形技術進行了大量研究，該工藝技術在市場上得到了廣泛應用。但國產同類不銹鋼管材質量與國外先進水平相比還有一定差距，特別是部分大中口徑、厚壁管材成形后的尺寸誤差、表面缺陷等問題比較突出，在一定程度上影響了產品質量。文中針對316L奧氏體不銹鋼直縫焊管JCOE生產技術，采用ANSYS有限元數值模擬技術，通過構建模型以及對彎曲成形質量進行深入分析，構建冷彎回彈曲線方程，對預彎曲量實施相應補償，實現JCOE管材精確成形，從而為該類型焊管成形技術奠定理論基礎。

1 彎曲回彈解析

板料彎曲是一種典型的彈塑性變形過程，當外力載荷卸除后，板料的體積和形狀必然產生部分回復，具體表現為彎曲角度和曲率半徑的變化。在彎曲初始階段，彎曲半徑比較大，內外部邊緣應力強度要遠遠低于屈服極限，在變形時表現出較強的全彈性彎曲[10-11]；隨著彎曲半徑的減小，變形區內外邊緣先進入塑性變形狀態，并向板料原始中性層位置擴展，此時板料處于彈塑性變形階段，且靠近中性層區域屬于純彈性應變狀態，應力隨厚度呈線性分布，這一區域外為彈塑性變形區，其應力大于屈服應力，應力–應變不再是線性關系[12-13]。下面為簡化彎曲回彈過程，進行如下假設[14]：（1）板料變形區的應力–應變狀態為“三向應力，平面應變”，在板料寬度方向上應變為0，在厚度方向上應變呈線性分布，遵循=/，其中為質點與中性層的距離，為中性層半徑，為應變；（2）靠近中性層區域，應力沿厚度方向呈線性分布，在此區域外呈非線性關系；（3）在彎曲過程中板料縱向纖維無擠壓，不存在纖維之間的橫向應力；（4）板料的彎曲變形被認為是理想彈塑性變形。

彎曲切向應力在彎板橫截面上合力必為0，即凸側拉應力與凹側壓應力之和為0，只需計算1/2截面上的應力再乘2即可，彎曲回彈反彎矩的計算見式（1）。

式中：為板料厚度；θ為切向應力。

可分解為彈性與彈塑性變形對應的瞬時回彈與滯后回彈所產生的彎矩，如式（2）所示。

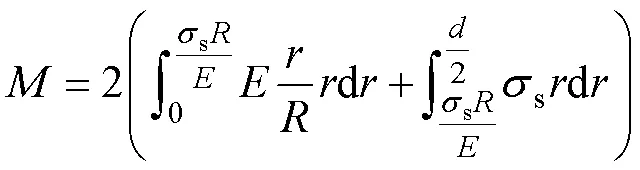
式中：為彈性模量；為回彈前彎曲半徑；s為屈服應力。對式（2）積分可得：

在彎曲后卸載過程中，可以認為在塑性變形反方向上增加一個理想的彈性彎矩?[15]，產生的等效彈性變形滿足式（4）。

進而求得等效彈性應變為：

式中：為回彈后彎曲半徑。

式（6）兩端同乘并整理后，得到關于回彈前彎曲半徑的一元三次方程，如式（7）所示。

根據回彈后彎曲半徑的屈服強度s以及板厚，可以直接計算獲得變形尺寸所需的彎曲半徑。

板料彎曲撓度分為直邊段與圓弧段2部分，且隨彎曲半徑的變化而變化，由幾何關系建立彎曲半徑與撓度的關系式見式（11），回彈量表征如圖1所示。

式中：為板料弧長；為板料直邊長；Δ0為回彈量；1為回彈后撓度；2為回彈前撓度。

圖1 回彈量表征

2 有限元模型

304L、316L、S32205、S31803等奧氏體不銹鋼具有耐低溫、抗氧化、耐腐蝕等特點，適用于海洋的復雜環境，而且具有超低溫韌性，在–100 ℃甚至更低的工作溫度下，能有效防止惡性脆性斷裂[16-18]，文中研究材質為316L不銹鋼，尺寸規格為20 mm× 400 mm×80 mm。

JCOE冷彎上模曲率半徑為250 mm，下模圓角半徑為30 mm，為保證變形精度，網格劃分選用六面體主導且中間密兩端疏的形式，板料中心150 mm段局部加密，該段網格劃分沿寬度方向、長度方向、厚度方向分別為120、32、8層，板料整體劃分共16 618個單元，上下模均為剛體。材料模型為雙線性強化模型，可以同時反映材料的彈性屬性和硬化效應，使材料變形前后應力分布更接近真實情況。設定彈性模量為196 GPa，塑性模量為1.87 GPa，初始屈服強度為238 MPa，抗拉強度為552 MPa，泊松比為0.3。假設在整個彎曲過程中板料與周圍介質無熱交換，接觸類型為有摩擦接觸，接觸法向剛度為0.1，構建的有限元模型如圖2所示。隨著上模持續下移，板料開始發生彈塑性變形，通過改變單一變量，提取有效節點應力、回彈量等數值，分析關鍵工藝參數對成形過程中應力–應變以及卸載回彈的耦合影響。

圖2 有限元模型的建立

3 工藝參數對板料回彈的影響

3.1 上模下壓量

在JCOE冷彎模擬中，上模下壓量以凸模剛接觸板料處為起點，凸模依次向下壓8、12、16 mm。此時下模開口量為150 mm，上模下行速度為4 mm/s，摩擦因數為0.15。如圖3a所示，隨著下壓量的增加，外層金屬承受的拉應力與內層金屬承受的壓應力均增大。當上模下壓量增大到16 mm時，如圖3b所示，最大應力沿接觸寬度向外大幅擴展，這主要是因為隨著上模下壓量的增加，板料彎曲角度過大，但由于受到下模開口量的限制，凸模中間區域與板料產生間隙，凸模兩側與板料發生部分接觸，如圖3c中板料中心位置與凸模之間的白色區域，此時板料變形區已不是此前的包覆狀態，彎曲塑性變形區增大。隨著下壓量的增加，加載時彎曲區最大周向應力向兩側擴展，致使所需成形彎曲力急劇增加，材料發生彈塑性變形，如圖3d所示。

以板料中性層中點作為中心，取長度100 mm作為彎曲回彈測試范圍，用撓度D來表示彎曲回彈量。如圖4a所示，沿著變形區，板料回彈分布大致呈二次函數曲線，回彈由彎曲中心向兩側減小。從圖4b可以看出，當上模下壓量為8～14 mm時，上模下壓量與板料彎曲最大回彈量呈線性關系，此時上模下壓量每增加2 mm，板料卸載回彈變化幅度不大，這對回彈控制十分有利，可以通過適當增加下壓量對彎曲進行補償，提高管材尺寸精度。然而，當下壓量增大到16 mm時，回彈量顯著增大，將不再遵循線性回彈規律。

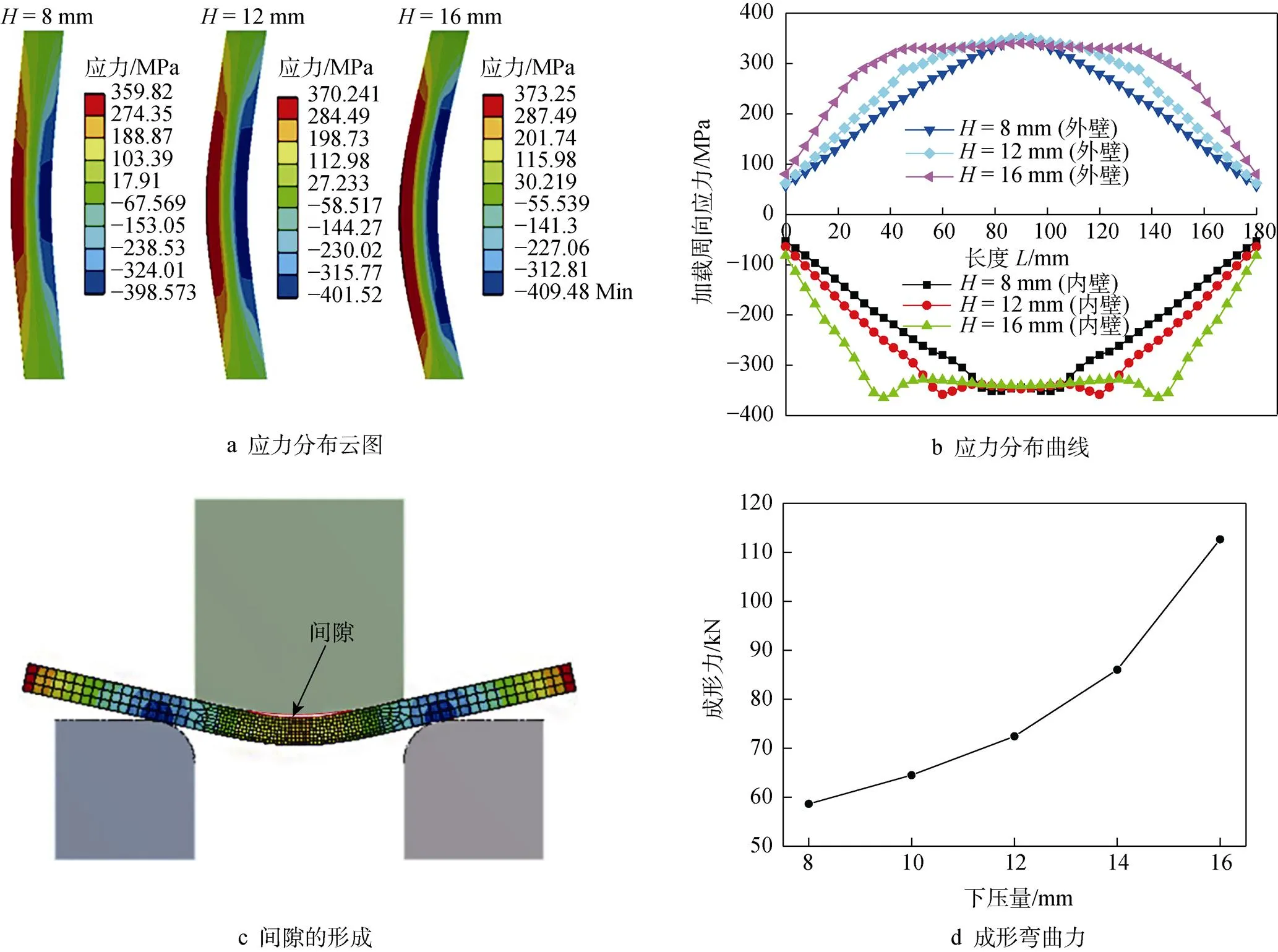
圖3 不同下壓量變形區應力分布

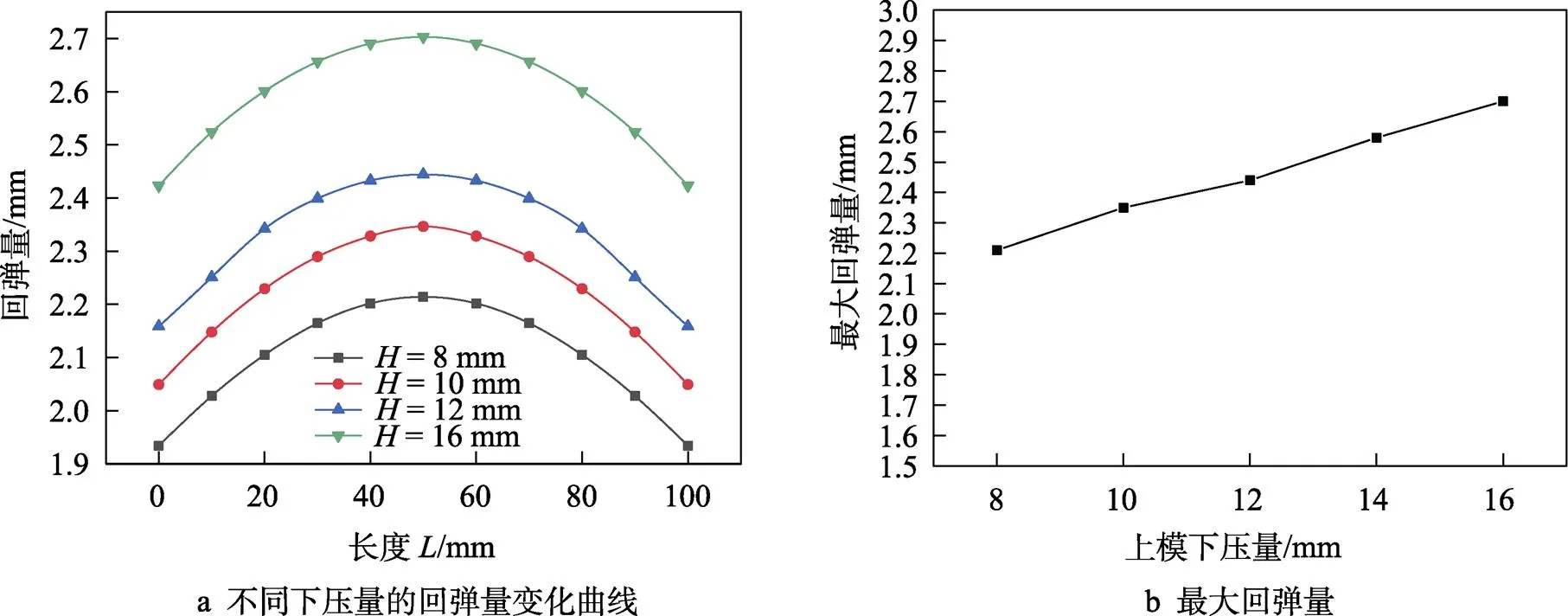
圖4 變形區回彈變化

3.2 上模下行速度

由于受到三點彎曲工藝及調速限制，模擬上模下行速度為2、4、6、8 mm/s，此時下模開口量為150 mm，上模下壓量為12 mm，摩擦因數為0.15。從圖5a可以看出，彎曲回彈量由彎曲中心向兩端迅速減小，且隨著下行速度的增大，板材回彈量有效降低。

考慮到模擬過程中上模下行速度變化范圍較小，材料屈服強度變化不大，因此可以認為隨著下行速度的增大，材料彈性變形能增大，彎曲回彈增大。在高速彎曲過程中，板材會產生變形熱和摩擦熱，促使金屬軟化，而且當這種高速變形軟化效應大于硬化效應時，卸載回彈減小[19-21]。如圖5b所示，當上模下行速度高于6 mm/s時，最大回彈量顯著降低，這正是由軟化效應導致的。此外，提高變形速度也會增加慣性效應，在一定程度上減小回彈量。

圖5 彎曲速度與回彈的關系

3.3 下模開口量

選取下模開口量為150～200 mm，以為10 mm為間隔，保證上模下壓量為12 mm、上模下行速度為4 mm/s、摩擦因數為0.15不變，進行有限元模擬。通過有限元模擬板料彎曲中間段回彈量如圖6a所示，可以看出，下模開口量在150～180 mm時板料回彈量變化較小，變化幅度約在0.05～0.17 mm之間。圖6b為不同開口量下彎曲中心區的最大回彈量，可以明顯看出，當開口量增至200 mm時，最大回彈量接近4 mm，卸載回彈最為顯著。

當上模下壓量一定，下模開口量越大，板料彎曲區變形程度越小，材料彈性變形所占比例越大，卸載后彎曲回彈量越大。過大的開口量會引起彎曲曲率半徑變化增大，與理想曲率偏差更大。相反，如果彎曲變形區減少，兩邊的直邊段會加長，如圖1所示，多道次成形影響管材圓度，為后續焊接和擴徑工藝造成質量隱患。為更好地控制冷彎回彈量，應使開口量控制在150～180 mm之間。

圖6 下模開口量與回彈的關系

3.4 摩擦因數

在板料彎曲變形過程中，發生的主要摩擦是下表面與下模圓角的相對滑移和上表面與上模之間的摩擦，模具及板料的粗糙程度對彎曲成形性及板材外表面質量有一定的影響。摩擦因數為0.05、0.15、0.25時的板料回彈量如圖7所示。可以看出，當摩擦因數為0.25時，回彈影響顯著，板料回彈量最大值為3.06 mm。這是由于在板料彎曲過程中，上模對板料的摩擦力沿切向方向向外，而內表面積不斷減小，板料表層的摩擦力將阻礙彎曲變形，卸載后回彈顯著。

綜合考慮，板料最佳冷彎成形工藝參數如下：上模下壓量為12 mm，下模開口量為150 mm，上模下行速度為4 mm/s，摩擦因數為0.15。

圖7 不同摩擦因數的彎曲回彈變化

4 回彈模型建立及驗證

4.1 回彈方程構建

在成形過程中，板料不僅受到材料力學性能的影響，還受到上述諸多幾何參數對回彈成形質量的耦合影響，因此需要對式（10）進行優化以提高計算精度。采用解析表達式逼近離散數據的方式對曲線擬合，通過方差分析曲線的擬合程度。

板料冷彎成形回彈量變化擬合曲線如圖8所示，由圖8可知，曲線擬合誤差不超過0.2%，對板料回彈影響顯著的因素依次為上模下壓量、下模開口量、上模下行速度和摩擦因數。上模下壓量和下模開口量與回彈量呈線性關系，上模下行速度和摩擦因數與回彈量呈指數關系。

圖8 各因素對回彈影響的擬合曲線

對回彈公式（10）進行修正，得到式（12）。

式中：?為優化后回彈計算值；?0為優化前回彈理論值；為綜合影響因子；k為上模下壓量影響因子；k為下模開口量影響因子；k為上模下行速度影響因子；k為摩擦因數影響因子。

根據圖8的擬合曲線，可以得到各影響因子的計算見式（13）。

4.2 試驗驗證

為驗證所構建的冷彎回彈曲線方程的精度，在JCOE成形機上，選擇尺寸規格分別為10 mm× 300 mm×1 800 mm、20 mm×450 mm×1 800 mm、30 mm×600 mm×1 800 mm的316L不銹鋼進行多道次冷彎實驗。

在多道次冷彎過程中，板料清潔平整不需做任何潤滑處理，在接觸區增加不同粗糙度的墊片來改變摩擦因數；在板料彎曲中心和直邊端點安裝發光標靶，采用發光成像儀記錄位移變化并記錄回彈量，求取平均值。多道次冷彎后樣品如圖9所示，徑壁比值≤10。

針對試驗使用的3種板材規格分別進行有限元回彈模擬和理論計算。圖10為冷彎回彈測量平均值與模擬值、計算值的對比情況。當板厚為20 mm時，模擬值、計算值和實測值數據吻合較好；當板厚為10 mm時，彎曲回彈模擬值偏差最大，但不大于5.5%。從圖10可以看出，理論計算值更接近于測量值，這主要是由于優化后的理論模型綜合考慮了諸多關鍵影響因素的耦合作用，更接近于真實彎曲工況。

圖9 JCOE成形試驗回彈測定

圖10 回彈對比

5 結論

1）基于寬板彎曲回彈理論，根據板料不同彎曲初始階段、彈塑性變形階段和塑性變形階段的應力–應變分布特征，綜合材料固有性能和板料幾何參數對回彈的影響，利用反彎矩及塑性變形條件，推導并建立了理想狀態下的冷彎回彈方程。

2）針對316L奧氏體不銹鋼直縫焊管JCOE生產技術，對該類板材的彎曲工藝過程進行深入研究。采用有限元仿真技術研究影響板材彎曲質量的因素，包括材料本身內在性能、上模下壓量、上模下行速度、下模開口量以及摩擦工況等對彎曲變形區應力分布、回彈分布以及最大回彈量的影響規律，闡明板料回彈變化特征，獲得了徑壁比值≤10時板料最佳冷彎成形工藝參數，即上模下壓量為12 mm，下模開口量為150 mm，上模下行速度為4 mm/s，摩擦因數為0.15。

3）有限元模擬結果表明，回彈量與上模下壓量、下模開口量呈線性關系，與上模下行速度、摩擦因數呈指數關系。綜合考慮影響回彈的主要工藝參數變化特征，對理想狀態下的冷彎回彈方程進一步優化，并在JCOE試驗機上進行多道次冷彎試驗，回彈計算結果與實測結果吻合較好。因此，構建的冷彎回彈方程可以為同類焊管冷彎質量控制提供重要理論基礎。

[1] LIU Yi-ke, ZHU Wei-lin, MI Li-jun, et al. Migration of Multiples from the South China Sea[J]. Science China Earth Sciences, 2015, 58(3): 482-490.

[2] 曾曉光, 金偉晨, 趙羿羽, 等. 海洋開發裝備技術發展現狀與未來趨勢研判[J]. 艦船科學技術, 2019, 41(17): 1-7.

ZENG Xiao-guang, JIN Wei-chen, ZHAO Yi-yu, et al. Current Situation and Development of Marine Development Equipment Technology[J]. Ship Science and Technology, 2019, 41(17): 1-7.

[3] REN Q, ZOU T, LI D, et al. Numerical Study on the X80 UOE Pipe Forming Process[J]. Journal of Materials Processing Technology, 2015, 215: 264-277.

[4] PHANITWONG W, BOOCHAKUL U, THIPPRAK-M-A-S S. Design of U-Geometry Parameters Using Statistical Analysis Techniques in the U-Bending Process[J]. Metals, 2017, 7(7): 235.

[5] ZHAO J, LI Jian, QU Xiao-yang, et al. Study on Intelligent Control Technology for Forming Steel Pipe of Pipeline with JCO Process[J]. Science China (Technological Sciences), 2011, 54(10): 2754-2759.

[6] GATTMAH J, OZTURK F, ORHAN S. Numerical Simulation of Bending Process for Steel Plate Using Finite Element Analysis[J]. Arabian Journal for Science and Engineering, 2019, 44(12): 10285-10292.

[7] POURBOGHRAT F, CHU E. Springback in Plane Strain Stretch/Draw Sheet Forming[J]. International Journal of Mechanical Sciences, 1995, 37(3): 327-341.

[8] PADGHAN N, DESHPANDE P, SAKHALE C. Force Analysis of Metal Sheet in Bending Operation on Sheet Bending Machine[J]. International Journal of Engine Research, 2015, 4: 267-270.

[9] 劉克進. 薄板沖壓回彈試驗研究及數值模擬對比分析[D]. 長沙: 湖南大學, 2004: 34-53.

LIU Ke-jin. Experimental Study on Springback and Its FEM Simulation Contrast in Sheet Matal Forming Process[D]. Changsha: Hunan University, 2004: 34-53.

[10] SU C, ZHAO J, GUO S. Analytical Description of Intelligent Controlled U-Free Bending Process in Wide Plate[J]. Materials Research Innovations, 2015, 19(5): 726-733.

[11] 馬海寬, 李培力, 隋健, 等. JCOE預彎成型工藝理論分析與有限元計算[J]. 化工設備與管道, 2014, 51(3): 65-69.

MA Hai-kuan, LI Pei-li, SUI Jian, et al. Theoretical and Finite Element Analysis for JCOE Pre-Bending Forming Process[J]. Process Equipment & Piping, 2014, 51(3): 65-69.

[12] 范利鋒, 梁培, 王葛, 等. 直縫焊管JCO成形非對稱彎曲變形過程分析[J]. 塑性工程學報, 2020, 27(2): 94-101.

FAN Li-feng, LIANG Pei, WANG Ge, et al. Research on Asymmetric Bending Process of JCO Forming for Straight-Seam Welded Pipe[J]. Journal of Plasticity Engineering, 2020, 27(2): 94-101.

[13] 李聰, 趙宏偉, 孫琳琳, 等. 45號鋼承載能力的原位三點彎曲試驗研究[J]. 東北大學學報(自然科學版), 2019, 40(6): 869-874.

LI Cong, ZHAO Hong-wei, SUN Lin-lin, et al. Research on Load Capabilities of 45#Steel via In-Situ Three-Point Bending Tests[J]. Journal of Northeastern University (Natural Science), 2019, 40(6): 869-874.

[14] 鄂大辛. 金屬管材彎曲理論及成形缺陷分析[M]. 北京: 北京理工大學出版社, 2016: 184-191.

E Da-xin. Metal Tube Bending: Theory and Forming Defects Anaiysis[M]. Beijing: Beijing Institute of Technology Press, 2016: 184-191.

[15] 馬燦. 大直徑厚壁管的成型技術[D]. 合肥: 合肥工業大學, 2010: 8-14.

MA Can. Forming Technology of Large-Diameter and Thick-Wall Tube[D]. Hefei: Hefei University of Technology, 2010: 8-14.

[16] WANG Jia-mei, ZHANG Le fu. Effects of Cold Deformation on Electrochemical Corrosion Behaviors of 304 Stainless Steel[J]. Anti-Corrosion Methods and Materials, 2017, 64(2): 252-262.

[17] 夏正文, 許全光, 馬世龍, 等. 316L不銹鋼焊管應變時效狀態的耐晶間腐蝕性能研究[J]. 焊管, 2021, 44(8): 7-10.

XIA Zheng-wen, XU Quan-guang, MA Shi-long, et al. Intergranular Corrosion Resistance of 316L Stainless Steel Welded Pipe under Strain Aging State[J]. Welded Pipe and Tube, 2021, 44(8): 7-10.

[18] ?RNEK C, ENGELBERG D. Towards Understanding the Effect of Deformation Mode on Stress Corrosion Cracking Susceptibility of Grade 2205 Duplex Stainless Steel[J]. Materials Science & Engineering A, 2016, 666: 269-279.

[19] FATHI H, EMADODDIN E, MOHAMMADIAN H R, et al. Effect of Punch Speed on the Formability Behavior of Austenitic Stainless Steel Type 304L[J]. Metals and Materials International, 2016, 22(3): 397-406.

[20] LIU B, VILLAVICENCIOC R, SOARES C G. Experimental and Numerical Analysis of Residual Stresses and Strains Induced during Cold Bending of Thick Steel Plates[J]. Marine Structures, 2018, 57(3): 121-132.

[21] 孔政, 張杰, 李洪波, 等. 摩擦系數對DP780鋼拉深成形極限的影響[J]. 塑性工程學報, 2018, 25(2): 252-259.

KONG Zheng, ZHANG Jie, LI Hong-bo, et al. Effects of Friction Coefficient on the Deep-Drawing Forming Limit of Dual-Phase Steel[J]. Journal of Plasticity Engineering, 2018, 25(2): 252-259.

Construction of Springback Curve Equation and Process Optimization of Welded Pipe during Cold Bending

ZHAO Yue-wei1, SHUAI Mei-rong1, CHU Zhi-bing1, GUI Hai-lian1, ZHAO Xiao-dong1, GAO Hong2, WU Li-hua3, ZHAI Li-li2

(1. Engineering Research Center of Heavy Machinery of the Ministry of Education, Taiyuan University of Science and Technology, Taiyuan 030024, China; 2. Wujin Stainless Steel Co., Ltd., Jiangsu Changzhou 213111, China; 3. Sinosteel Stainless Steel Pipe Technology (Shanxi) Co., Ltd., Taiyuan 030600, China)

The work aims to study the bending unloading springback and stress distribution characteristics of 316L austenitic stainless steel plate JCOE and impose corresponding compensation to pre-bending value, to improve the bending accuracy. Based on the elastic-plastic deformation theory, the effects of key forming parameters on plate bending and unloading springback were studied by finite element simulation method. The equation of springback curve was also established through linear/nonlinear fitting and superposition of affecting parameters. The springback had a linear relationship with the displacement of upper mold and the opening degree of lower mold, but had an exponential relationship with the speed of upper mold and the friction coefficient. The optimal parameters are as follow: the displacement of upper mold is 12 mm, the opening degree of lower mold is 150 mm, the speed of upper mold is 4 mm/s, and the friction coefficient is 0.15. The calculated bending springback value is in good agreement with the measured average value for the plate with diameter-wall ratio ≤10. The established model can provide a theoretical foundation for the practical production.

cold bending of welded pipe; springback analysis; construction of springback equation; optimization process

10.3969/j.issn.1674-6457.2022.07.014

TG316

A

1674-6457(2022)07-0098-08

2021–11–29

國家自然科學基金（U1710113）；常州市領軍型創新人才引進培育項目（CQ20200042）；山西省重點研發計劃（201903D121043）；山西省研究生教育改革研究課題（2020YJJG241）

趙月偉（1996—），男，碩士生，主要研究方向為金屬彎曲成形。

帥美榮（1978—），女，博士，教授，主要研究方向為金屬塑性變形理論與技術。

責任編輯：蔣紅晨