與等腰三角形相關(guān)的結(jié)論

劉頓

等腰三角形是一類特殊而又十分重要的三角形，它除了我們在課本中學(xué)習(xí)到的性質(zhì)外，還有許多的特殊結(jié)論，這些結(jié)論在今后的學(xué)習(xí)與運用中都可以起到重要的作用，現(xiàn)就等腰三角形的常見結(jié)論簡單歸納如下，供大家學(xué)習(xí)時參考！

1 等腰三角形底邊的中線上一點到兩腰的距離相等，這里的中線也可以改成頂角的平分線或底邊上的高

例1 圖1

已知如圖1，在△ABC中，AB=AC，AD為BC邊上的中線，P為AD上的任一點，PE⊥AB，PF⊥AC.

求證：PE=PF.

分析 依題意，由AB=AC，D為BC中點，利用等腰三角形的“三線合一”性質(zhì)得到AD為頂角的平分線，根據(jù)角平分線上的點到角兩邊的距離相等即可得到DE=DF.

證明 因為AB=AC，AD為BC邊上的中線，

所以AD平分∠BAC，

因為PE⊥AB，PF⊥AC，

所以PE=PF.

說明 本題主要考查等腰三角形的性質(zhì)的應(yīng)用，關(guān)鍵是掌握等腰三角形的腰相等且底邊上的兩個角相等，及角平分線上的點到角兩邊的距離相等.

2 等腰三角形一腰上的高與底邊的夾角等于頂角的一半

例2 圖2

已知如圖2，△ABC是等腰銳角三角形，AB=AC，CD是腰AB上的高.求證：∠BCD=12∠A.

分析 依題意，可通過輔助線構(gòu)建直角三角形來求解.如圖，過點A作底邊BC的垂線AE，垂足為E，那么∠EAB和∠DCB同為∠B的余角，因此這兩角相等;根據(jù)等腰三角形三線合一的特點，可得出∠EAB是頂角的一半，由此可得出所求的結(jié)論.

證明 過點A作AE⊥BC于點E，

所以∠EAB+∠B=90°，

因為CD⊥AB，

所以∠DCB+∠B=90°，

所以∠DCB=∠EAB，

因為AB=AC，AE⊥BC，

所以∠EAB=∠BAC，

所以∠DCB=12∠BAC.

說明 此題主要考查學(xué)生對等腰三角形性質(zhì)的理解及運用;作出輔助線是正確解答本題的關(guān)鍵.另外，在本題中無需考慮等腰三角形的頂角是銳角或直角或鈍角.

3 等腰三角形底邊上一點到兩腰的距離之和等于一腰上的高;等腰三角形底邊延長上一點到兩腰的距離之差等于一腰上的高

例3 已知在△ABC中，AB=AC，D為BC上任意一點，DE⊥AB，DF⊥AC，垂足為E，F(xiàn)，CG⊥AB于G，求證：CG=DE+DF.

分析 可依題意畫出符合題意的圖形，連接AD，由圖形結(jié)合三角形的面積公式，利用等腰三角形的性質(zhì)即可求解.

證明 如圖4，因為ED⊥AB，

所以S△ABD=12AB·ED;

因為DF⊥AC，

所以S△ACD=12AC·DF;

因為CG⊥AB，

所以S△ABC=12AB·CG.

又因為AB=AC，

S△ABC=S△ABD+S△ACD，

所以12AB·CG=12AB·ED+12AC·DF，

所以CG=DE+DF.

說明 “等腰三角形底邊延長上一點到兩腰的距離之差等于一腰上的高”同樣可以利用三角形的面積關(guān)系，依照本題的證明方法求解.

4 以直角三角形的直角邊為腰銳角頂點為頂點在形內(nèi)分別作等腰三角形，所得公共角等于45°

例4 圖5

如圖5，在Rt△ABC中，∠ACB=90°，點D，E在邊AB上，且AD=AC，BE=BC，求∠DCE的度數(shù).

分析 依題意可由等腰三角形的性質(zhì)得出∠ACD=∠ADC，∠BCE=∠BEC，再利用三角形內(nèi)角和定理進一步求出∠ACD+∠BCE=135°，進而求解.

解 （1）因為AD=AC，BC=BE，

所以∠ACD=∠ADC，

∠BCE=∠BEC，

所以∠ACD=12（180°-∠A），

∠BCE=12（180°-∠B），

因為∠A+∠B=90°，

所以∠ACD+∠BCE=180°-12（∠A+∠B）

=180°-45°=135°，

所以∠DCE=∠ACD+∠BCE-∠ACB

=135°-90°=45°.

說明 本題考查了等腰三角形的性質(zhì)，三角形內(nèi)角和定理，運用數(shù)形結(jié)合、整體思想是解題的關(guān)鍵.

5 等腰三角形一腰上的垂直平分線與底邊相交所成的銳角等于頂角的一半

例5 在△ABC中，AB=AC，AB的垂直平分線交AC于點N，交BC的延長線于點M，∠A=40°.

（1）求∠NMB的大小.

（2）如果將（1）中的∠A的度數(shù)改為70°，其余條件不變，再求∠NMB的大小.

（3）你認(rèn)為存在什么樣的規(guī)律？試用一句話說明.（請同學(xué)們自己畫圖）

（4）將（1）中的∠A改為鈍角，對這個問題規(guī)律的認(rèn)識是否需要加以修改？

分析 （1）由在△ABC中，AB=AC，∠A=40°，根據(jù)等腰三角形的性質(zhì)，可求得∠ABC的度數(shù)，又由AB的垂直平分線交AC于點N，交BC的延長線于點M，即可求得答案;

（2）由在△ABC中，AB=AC，∠A=70°，根據(jù)等腰三角形的性質(zhì)，可求得∠ABC的度數(shù)，又由AB的垂直平分線交AC于點N，交BC的延長線于點M，即可求得答案;

（3）由在△ABC中，AB=AC，根據(jù)等腰三角形的性質(zhì)，即可用∠A表示出∠ABC，又由AB的垂直平分線交AC于點N，交BC的延長線于點M，即可求得答案.

（4）由以上證明方法可得答案.

解 （1）因為在△ABC中，

AB=AC，

∠A=40°，

所以∠ABC=∠ACB=70°，

因為AB的垂直平分線交AC于點N，交BC的延長線于點M，

所以MN⊥AB，

所以∠NMB=90°-∠ABC=20°.

（2）因為在△ABC中，

AB=AC，

∠A=70°，

所以∠ABC=∠ACB=55°，

因為AB的垂直平分線交AC于點N，交BC的延長線于點M，

所以MN⊥AB，

所以∠NMB=90°-∠ABC=35°.

（3）等腰三角形一腰上的中垂線與底邊延長線所成夾角度數(shù)是頂角的一半，即

∠NMB=12∠A.

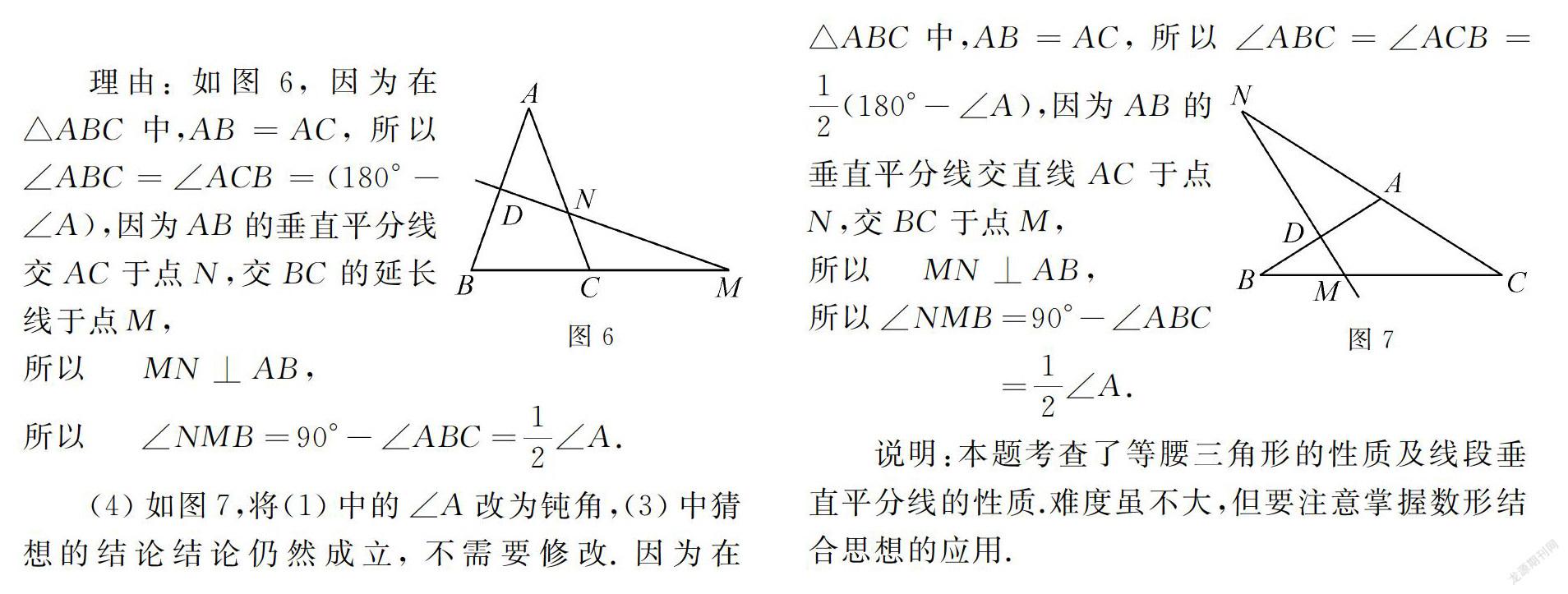
理由：如圖6，因為在△ABC中，AB=AC，所以∠ABC=∠ACB=（180°-∠A），因為AB的垂直平分線交AC于點N，交BC的延長線于點M，

所以MN⊥AB，

所以∠NMB=90°-∠ABC=12∠A.

（4）如圖7，將（1）中的∠A改為鈍角，（3）中猜想的結(jié)論結(jié)論仍然成立，不需要修改.因為在△ABC中，AB=AC，所以∠ABC=∠ACB=12（180°-∠A），圖7因為AB的垂直平分線交直線AC于點N，交BC于點M，

所以MN⊥AB，

所以∠NMB=90°-∠ABC

=12∠A.

說明：本題考查了等腰三角形的性質(zhì)及線段垂直平分線的性質(zhì).難度雖不大，但要注意掌握數(shù)形結(jié)合思想的應(yīng)用.