MATLAB 在數學建模中的應用

周瀛

（長春建筑學院,吉林 長春 130604）

1 MATLAB 的功能和特點

MATLAB 是一種用于算法開發、數據可視化、數據分析及數值計算的高級技術計算語言和交互式環境，具有如下特點：

a.計算功能強大。

b.圖形展示功能強大。MATLAB 強大的繪圖功能使得數據的可視化變得非常簡單。

c.工具箱功能強大。MATLAB 包含大量已編寫程序，用戶可直接進行計算、圖示建模仿真及其他相關研究。

d.幫助功能完整。

2 數學建模的一般步驟

數學建模的過程大概可以分為以下幾個步驟：

a.根據實際問題，明確建模目的，收集必要數據資料。

b.分析數據資料，提出若干符合實際背景的假設。

c.抽象并簡化變量及參數間的關系，建立數學模型。

d.根據模型特點選取適當方法進行模型求解。

e.模型分析與檢驗，即用實際問題的實測數據驗證模型是否可靠。

3 建模實例：道路交通流問題

為解決城市道路交通擁堵問題，提高預測道路交通流狀態的準確性，交警部門提供了局部區域7 日內道路的互聯網導航平臺數據、浮動車數據以及交通卡口監測數據。根據所提供的數據進行以下問題的研究：

a.構建模型描述道路交通流實際狀態，并比較分析說明模型特點。

b.構建指標用以直觀描述路段的暢通程度，基于采集數據計算所有路段的暢通程度。

c.構建模型進行道路擁堵預測，在道路發生擁堵后的任何時間點，基于已獲取的歷史監測擁數據，可以進行道路堵變化的預測。

3.1 問題假設

3.1.1 每條道路都沒有車輛出現故障或發生交通事故。

3.1.2 卡口數據、浮動車數據等實時數據在采集過程中不受極端天氣影響。

3.1.3 車輛在單位小時內的運動為勻速運動。

3.1.4 各變量因素之間不存在間接影響。

3.2 模型的建立與求解

3.2.1 問題一

3.2.1.1 數據處理

第一，整理不同時間段各個路段的交通流量數據，并對缺失數據作出缺失處理；第二，將時間段進行劃分，以1 小時為單位作為觀測時長，將七天時間劃分成168 個時間段；第三，結合卡口數據，統計各個道路單位時間內駛向不同方向的車輛數。

3.2.1.2 模型建立

交通流必須具備兩個條件：一是在道路上，二是在運行中。本文認為在足夠短的時間內交通流保持連續性不變。定義交通流量Q 的計算方法：

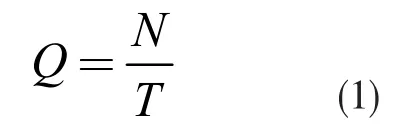
其中，T 為觀測時長(小時)；N 為T 小時內通過的車輛數。

3.2.1.3 模型求解

城市道路基礎設施狀況是影響交通流量的因子，很大程度上決定了交通流量具有非線性和不確定性[4]，但人們出行行為具有總體規律性，一定程度上又決定了交通流量具有時空相似性。經過求解公式(1)，得到各條路段在不同時間段內的交通流量，利用MATLAB 繪制出每個路段七天的交通流量圖如圖1 所示（以路段一為例，其余各路段類似）：

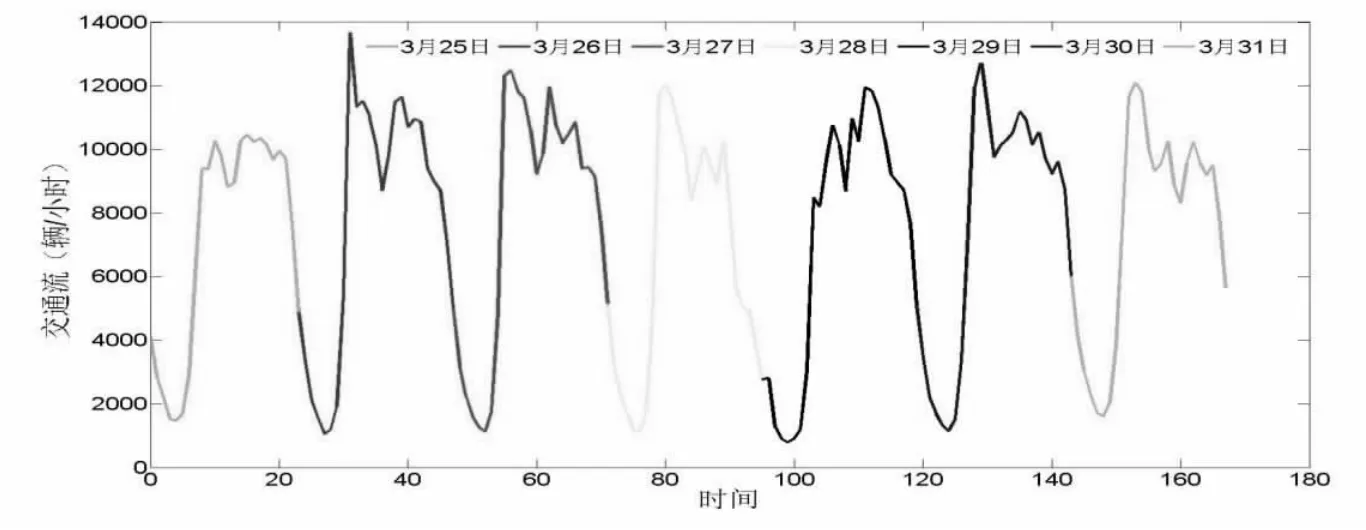
圖1 路段一交通流實際狀態

通過分析發現，交通流量具有時間相似性，即同一地理位置或同一區域的人們出行時間具有規律性，例如各路段在通勤日或雙休日具有相似的交通流特點，在同一天內達到流量高峰的時間段基本相同。

3.2.2 問題二

3.2.2.1 數據處理

基于問題一歸納整理出任一位置的實際交通流量，利用MATLAB 軟件中的“max”函數統計出每條道路的最大交通流量。依據道路所占權重進行回歸擬合，統計出通勤日與周末的車流量，進而衡量道路暢通程度。

3.2.2.2 模型建立

同一條件的道路同一時刻不同位置截面所通過的車輛數目不同，則這條道路任一位置的暢通程度[5]不同。路網中有n 條路段，i 時刻道路j 的暢通概率定義為道路在某一時刻交通狀態等級處于可接受狀態的路段暢通程度，計算方法如下：

其中，Q(i,j)為實際交通流量；為道路j的最大交通流量且=maxQ(i,j)；-Q(i,j)表示道路剩余交通流量。

為了使評價結果具有一致性，基于問題一所統計的數據，利用卡口數據進行平均交通流量(i,j)的回歸擬合分析，如下：

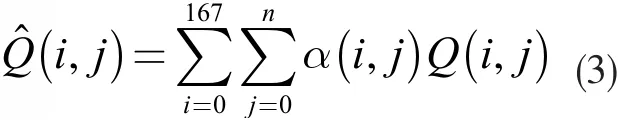
其中，α (i,j)表示道路j第i 時刻交通流量所占權重值。通過隸屬函數 μ建立起與暢通概率P(i,j)之間一對一的關系，公式如下：

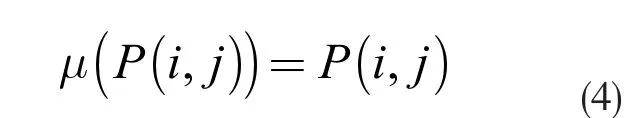
用隸屬函數 μ作為評價道路路段暢通程度的指標，將隸屬度區間[0,1]劃分為四個區間，每個區間對應一類評估詞，劃分結果見表1：

表1 擁堵程度表

3.2.2.3 模型求解

利用MATLAB 擬合出隸屬度關于時間的函數圖像，如圖2（以路段一為例，其余各路段類似）：

對比表1，由圖2 可以發現，該路段在通勤日的暢通程度如下：00:00～06:30 期間車輛來往較少，路段處于暢通狀態；06:30～07:00 期間開始進入早高峰，路段變得非常擁堵；07:00～11:00 期間路段持續非常擁堵；11:00～13:00 期間車輛稍有減少，路段進入擁堵狀態；13:00～21:00期間路段再次進入非常擁堵狀態，21:00 以后路段逐漸由非常擁堵狀態進入基本暢通狀態。

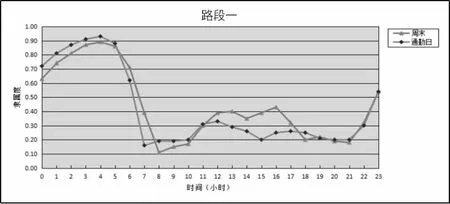
圖2 路段一暢通程度

3.2.3 問題三

3.2.3.1 數據處理

對道路網數據以及浮動車軌跡數據進行篩選與關聯，剔除部分異常數據，將車速小于或等于某一特定值時作為判斷為堵車時的速度，將速度為0 的數據全部篩選出來。在道路發生擁堵后的任一時間點，統計出同一時刻不同道路的當前車流量，進一步與最大交通流作比較，分析擁堵程度并預測擁堵變化。

3.2.3.2 模型建立

聚類分析可根據對象之間的相似程度將對象劃分為幾個類別，是一種非常重要和有效的無監督分類方法[6]。本文采用模糊聚類分析理論中的FCM 算法進行道路擁堵預測。考慮樣本集X= {x1,x2,…,xn}，其中xi={xi1,xi2, …,xik}，將X 分為k個模糊子集，聚類結果由聚類中心矩陣C= {c1,c2, …,ck}及隸屬度矩陣μ共同表示：

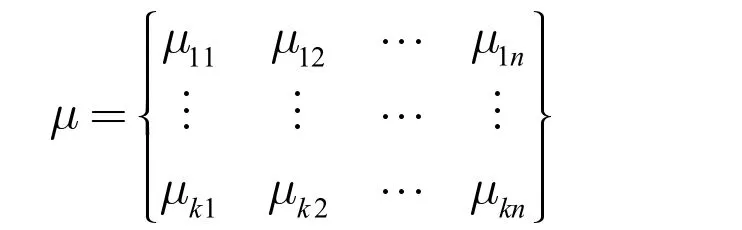
FCM 算法的數學描述為：

(1) 設定聚類數k、指數權重m 及停止閾值 ε；初始化聚類中心C(0)；設置計數器b=0。

(2) 計算模糊隸屬度矩陣 μ(b)：

(3) 計算新的模糊聚類中心C(b+1)：

本文選擇模糊綜合評判方法實現對路網交通狀態的實時評價，步驟如下：

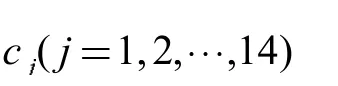
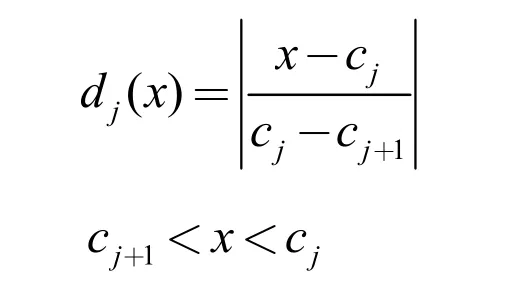
并認為兩者的關聯度越高，指標x 屬于類別j 的隸屬度越高。

步驟2：計算模糊隸屬度矩陣

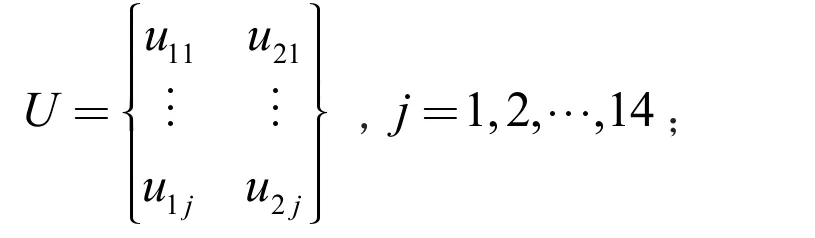
步驟3：為路網暢通率和路網負荷裕度賦予權重W=(w1,w2)，對于不同的指標，如果交通管理者對其關注程度高，則賦予其較高的權值；否則，賦予較低的權值。

步驟4：計算綜合評價矩陣B=W?U，其中

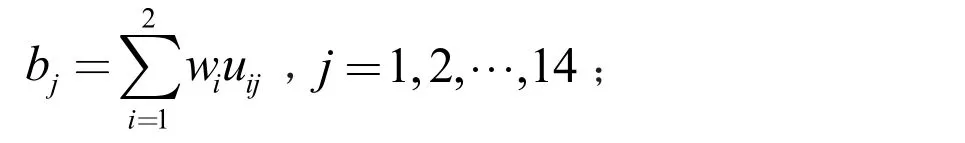
步驟5：確定最終輸出結果b*=max (b1,b2, …,b14)。

3.2.3.3 模型求解

采用K 均值聚類分析法，利用MATLAB[5]軟件實現，經過對坐標和時間的兩次聚類后，得到聚類結果。為了刻畫不同路口在各個時間段的擁堵程度，用表示路口，時間段為t= {t0,t1, …,t23}，將同一時間段內的不同路口的交通流量最大值記為qmax(t,l)，最小值記為qmin(t,l)，不同路口在各個時間段的擁堵程度，記作ω(t,l)，關系式如下：

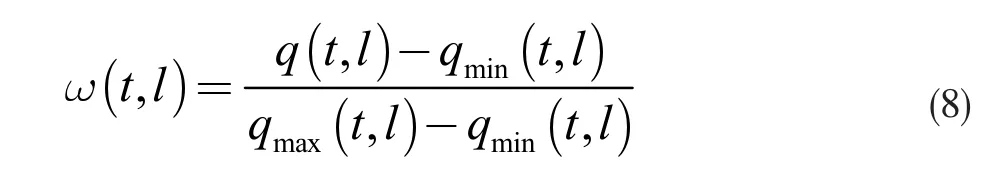
其中，q(t,l)為第l 個路口的第t 個時間段內的交通流量以其中一個路口L1為例，給出t1～t12交通擁堵程度表(其余類似)如表2。

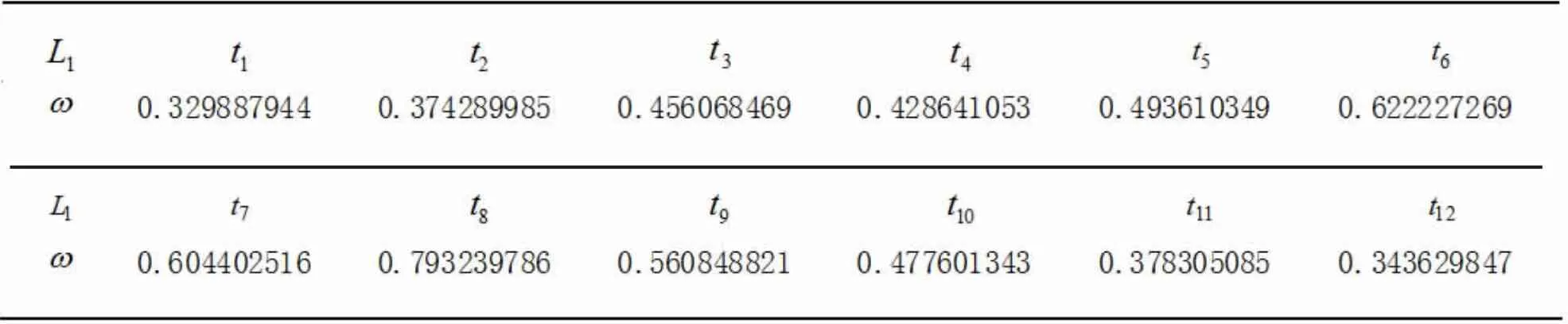
表2 路口L1 交通擁堵程度

3.2.4 模型的分析檢驗

第一，模型的穩定性好。利用MATLAB 軟件對處理后的數據進行畫圖分析，輸出的圖像能準確地看出實際交通流的變化特征，易發現其規律性；第二模型的層次性好，試用范圍廣，易于推廣。利用MATLAB 軟件對大數據進行K 均值聚類法，算法快速簡單；第三，模型尚有不足之處，對缺失數據的處理方法有待改進，改進后可減小由于數據缺失造成的誤差。

4 結論

通過上述模型的求解過程不難發現，MATLAB 強大的數值計算功能、圖形展示功能及編程功能使其在解決數學建模問題時展現出其它軟件無法比擬的優勢。將MATLAB 應用于數學建模的過程中必將能夠使數學模型更好地反映實際問題的本質屬性。