基于GWO-MLP的光伏系統輸出功率短期預測模型

張惠娟，劉琪，岑澤堯，李玲玲

(1.河北工業大學 電氣工程學院 省部共建電工裝備可靠性與智能化國家重點實驗室，天津 300130； 2.河北省電磁場與電器可靠性實驗室，天津 300130)

0 引 言

隨著社會進步與經濟發展，傳統能源對環境的污染嚴重影響人類的日常生活，如何高效利用清潔能源、實現綠色GDP是當今社會的重要目標。太陽能作為當今世界發展較為迅猛的可再生清潔能源之一，憑借其自身無需開采運輸、無噪聲、無污染等優點而被作為替代能源得以廣泛地接受，這是實現綠色經濟、完善低碳產業鏈的一條十分重要且關鍵的途徑。對此，為了減輕已建成的光伏發電系統對現有電力系統運行方面的安全性、穩定性所造成的影響，對其輸出功率進行高精確度、強準確性的短期預測就成為一項重要的工作。該工作可以有效提高清潔能源的滲透水平，實現電網調度的安全、實時、動態運行，進而增強電力系統的穩定性、可靠性、安全性以及經濟性[1]。

在眾多預測方法中，中短期預測往往結合數值天氣預報，并且采用物理方法進行預測，短期和超短期預測則常采用統計法。文獻[2]中所述的預測方法是將與目標日相似的歷史數據用于預測目標日的輸出功率，此方法在小型光伏發電系統中達到了比較滿意的預測精度和準確度。針對統計方法的光伏發電系統輸出功率預測，已有的預測方法包括：馬爾科夫鏈模型[3]、灰色理論[4]、多元線性回歸模型[5]、自回歸滑動平均模型、人工神經網絡[6]、貝葉斯模型[7]等。上述方法各有其特點，但也存在一些不足。直接預測方法中用到的神經網絡和支持向量機等均屬于淺層機器算法，這些算法的建模和表征能力有限，無法對高維數據進行有效的特征提取，訓練過程也比較復雜，要想對具有間歇性、隨機性特點的光伏發電系統輸出功率進行可靠預測，就會有一定難度， 無法得到十分準確的預測結果。對于一些外在隨機因素或極端天氣情況，多元回歸方法會由于考慮不足而導致預測結果誤差較大。自回歸滑動平均模型對結果預測的準確性高，但預測誤差會因為高密度的歷史數據和較大時間跨度的待預測時間而增大。原始數據的準確程度以及天氣條件的復雜程度對基于馬爾科夫鏈方法預測的精度有著很深的影響，當馬爾科夫鏈轉移矩陣具有較高階數時，對光伏發電的輸出功率進行預測將無任何意義。基于灰色理論的光伏輸出功率預測模型不要求輸入大量的光伏數據，預測的精確程度相對較高，但是預測的準確程度不穩定，此外，預測結果會由于天氣狀況具有較大的起伏。解決這一問題的可行途徑是將上述方法中的幾種(多為兩種)結合起來使用，或者在原有算法的基礎上增加一個“預處理”環節，從而在預測時把數值天氣預報和氣象因素歷史數據等信息考慮在內。文獻[8]提出一種基于灰色理論和神經網絡的組合模型，首先依據相似日來建立各時刻出力的灰色模型，得到輸出結果，再用此結果和樣本日的溫度數據搭建神經網絡。文獻[9]提出的預測方法是把小波分解和神經網絡相結合，在尺度方面分解光伏功率序列，以此得到一種低頻分量和兩種高頻分量，各層神經網絡的輸入為太陽輻照量序列，通過神經網絡和小波重構預測光伏輸出功率。文獻[10]人提出將人工神將網絡與模擬組合法相結合的預測方法，生成一個以氣象和環境為參數的預測函數，人工神經網絡用于進行確定性預測，模擬組合法用于進行確定性和概率性預測。文獻[11]將多層感知機(Multi Layer Perceptron，MLP)應用于光伏功率短期預測中，取得了較為滿意的結果，但由于MLP的初始權重和偏置量為隨機初始形成，在訓練過程中常常容易陷入局部最優解的困境，進而導致訓練誤差的增大。灰狼優化算法(Grey Wolf Optimizer，GWO)[12]是近幾年提出的一種種群優化算法，已經在光伏發電系統的最大功率點追蹤[13]、智能電網控制[14]等領域取得了不錯的效果。

針對現有預測方法的缺陷，文章提出一種基于改進灰狼優化算法優化MLP的初始權重和偏置量的光伏系統輸出功率短期預測模型。預測結果表明，所提出的方法具有更快的收斂速度和更高的預測精度。

1 MLP神經網絡模型

MLP[15]作為一種具有深度學習能力的前向神經網絡，在多層網絡中包含大量神經元，可映射一組輸入向量到一組輸出向量，理論上可以任意精度近似任何線性連續函數，這一優勢促進MLP神經網絡在語音分析、影像分析、智能器械等方面的應用發展。

MLP一般為三層或者多層，其模型如圖1所示。

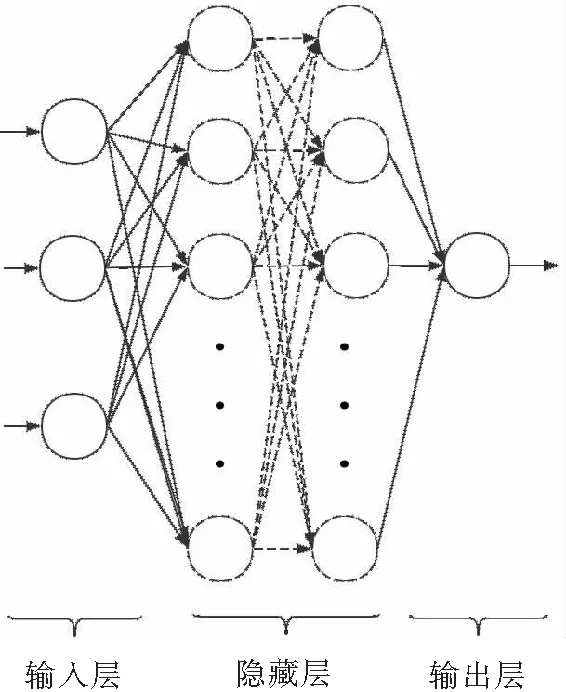
圖1 MLP模型結構圖Fig.1 Structure diagram of MLP model

由輸入層(一層)、隱藏層(一層或多層)和輸出層(一層)三部分組成。位于同一層的神經元，彼此之間無直接聯系，相鄰層的神經元之間經過權值加和實現全連接。數據由輸入層進入MLP后，隱藏層的神經元對其進行分析傳遞，最后由輸出層進行數據輸出，從而實現數據的多層優化處理。MLP神經網絡可以有多個輸入量和多個輸出量，依據需求目標來確定輸入層和輸出層的神經元個數；至于隱藏層的層數和每層的神經元個數，則是根據設定的誤差要求而定。MLP模型中，上一層的輸出即為下一層的輸入，對于隱藏層和輸出層中的神經元，第i層中第j個神經元的輸出公式為：

(1)

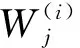
(2)

假設MLP神經網絡有m層(m≥3)輸出層只有一個神經元，類比式(1)可知，輸出層的輸出公式為：

Y=f(m)(W(m)·y(m-1)+b(m))

(3)

式中Y表示輸出；W(m)為第m層的權重向量，y(m-1)為第m-1層的輸出向量；b(m)為第m層偏置向量。

除了輸入層的神經元，其余神經元均為多輸入-單輸出，并且帶有非線性激活函數。權重向量W和偏置向量b由MLP的訓練過程確定，MLP神經網絡在訓練中能夠進行自學習與反饋調節，從而對各個神經元的權重和偏置量進行修正與調整，此過程可采用算法優化MLP的權重和偏置量，使MLP的輸出值更加逼近真實值，提高MLP模型的后期預測精度。

2 灰狼優化算法優化MLP模型

2.1 灰狼算法基本原理

灰狼優化算法(Grey Wolf Optimizer，GWO)作為一種新興、高效算法，其按照灰狼種群內部階層、狩獵特征和搜索行為進行建模。其狩獵過程大致分為：追蹤、接近獵物；圍捕獵物；捕獲獵物。

(1)社會等級。灰狼種群內部根據等級制度進行個體劃分，在GWO算法中，將狼群分為4種等級：α狼代表目前最優解，β狼表示第二優解，δ狼代表第三優解，其余解為ω狼。在GWO算法中，α狼、β狼和δ狼的任務是指引ω狼對獵物進行追趕捕捉，最后取得目標獵物。

(2)圍捕行為。圍捕行為的數學模型如下：

D=|C·Xp(t)-X(t)|

(4)

X(t+1)=Xp(t)-A·D

(5)

式中D表示灰狼與獵物相隔的長度；t表示目前迭代次數；Xp表示獵物的坐標矢量；X表示灰狼的坐標矢量；矢量A和C為參數。A和C的計算公式如下：

A=2a·r1-a

(6)

C=2·r2

(7)

在迭代過程中，a由2依次遞減到0，r1和r2為區間[0,1]內的隨機向量。

(3)狩獵行為。灰狼有很強的辨認獵物坐標的能力，一旦搜尋到獵物的蹤跡，就立刻對獵物進行捕捉。為了清晰表述灰狼捕捉獵物的過程，設定α、β和δ狼已經清楚獵物所處地點，其余灰狼位置的更新則會根據這三者的坐標來進行。灰狼群體更新自身坐標的公式如下：

Dα=|C1·Xα(t)-X(t)|

(8)

Dβ=|C2·Xβ(t)-X(t)|

(9)

Dδ=|C3·Xδ(t)-X(t)|

(10)

X1=Xα(t)-A1·Dα

(11)

X2=Xβ(t)-A2·Dβ

(12)

X3=Xδ(t)-A3·Dδ

(13)

(14)

(4)攻擊獵物。當獵物位置不再變化時，灰狼群體會通過逐漸縮小圍攻的范圍來完成狩獵。在GWO中表現為通過減小a的值來模擬灰狼靠近獵物的過程，這樣A的變化范圍也隨之縮小。在迭代過程中，當a從2減小到0的過程中，A是[-a,a]內的一個隨機數。當|A|<1時，灰狼的下一個坐標可以是當前所處坐標和獵物坐標之間的任意一點，狼群開始向獵物發起圍攻。

(5)尋找獵物。灰狼通過α 、β 和δ 狼的位置來尋找獵物。它們先各自搜索，再集體攻擊獵物。為了在數學模型上模擬灰狼的搜索行為，當|A|>1時迫使灰狼群體遠離獵物，以此來加強算法的全局搜索能力，尋找最為合適的獵物。在GWO算法中，利于搜索、追蹤的另一參數是C。C是隨機向量，位于區間[0,2]內，為α 、β 和 δ 狼提供隨機的權重，幫助GWO在優化過程中展現一個隨機的行為，更好地探索和避免陷入局部最優。

2.2 GWO的改進

在解決實際問題時，往往不能通過先前的經驗知識去了解GWO全局最優解的范圍，因此，初始種群的質量在一定程度上影響著GWO算法的收斂速度、收斂精度和尋優方向。初始種群的多樣性好、品質高，GWO算法尋找最優解的能力就越強，迭代次數越少。傳統GWO算法存在缺點：不能歷遍群體內的每個個體，容易陷入局部最優解的困境，并且初始種群的產生具有很強的隨機性，不利于提高算法的搜索速度和搜索所用時間。

具有隨機性和普適性的混沌理論是對沒有準確預測可能并且無規律可循的現象及過程的認識，其在優化目標、改進函數方面有著廣泛應用[16]，其中， Logistic映射[17]可產生滿足一定統計要求的序列，其表達式如下:

x(t+1)=μx(t)(1-x(t))

(15)

因此，針對傳統GWO算法的不足，可以選擇Logistic映射來優化GWO的初始種群，從而獲得質量較好的初始種群，具體過程如下：

(1)給定參數μ和迭代次數k；

(2)設置種群迭代的初始值；

(3)使用式(15)對初始值進行映射運算；

(4)判斷是否滿足迭代停止條件，如滿足迭代條件，執行(5)，否則返回(3)；

(5)獲得高質量的GWO初始種群。

2.3 改進GWO優化MLP

改進后的GWO作為一種優化算法，其優化對象為MLP模型中每層神經網絡的初始權重和偏置量，將每層網絡中的權重矩陣和偏置量矩陣依次展開并組成行向量，將此行向量作為GWO初始種群的一個個體，GWO依次歷遍所有個體，根據適應度函數值選出本代的α狼、β狼和δ狼。GWO重復迭代至滿足停止所要求的條件，輸出的最優解即為挑選出的α狼。隨后將α狼個體依次拆分成為MLP神經網絡的初始權重矩陣和偏置量矩陣，分配給MLP進行訓練。

GWO尋優的流程如下：

(1)搭建MLP模型結構。根據待解決問題的輸入參數數量以及輸出目標個數來確定MLP輸入層和輸出層的神經元數目，并設置隱藏層的層數和每層神經元的個數；

(2)設置GWO參數。如最大迭代次數；

(3)初始化GWO狼群的位置；

(4)計算灰狼種群中每個個體的適應度函數值，挑選出α狼、β狼和δ狼；

(5)根據式(8)～式(14)更新狼群中每個個體的位置信息；

(6)判斷是否滿足結束所需條件，如滿足執行(7)若不滿足，返回步驟(4)；

(7)輸出α狼的位置向量；

(8)根據MLP結構拆分α狼行向量組成初始權重矩陣和偏置量矩陣。

3 基于GWO-MLP的光伏系統輸出功率短期預測

3.1 預測流程

采用GWO-MLP預測光伏系統輸出功率的流程圖如圖2所示。

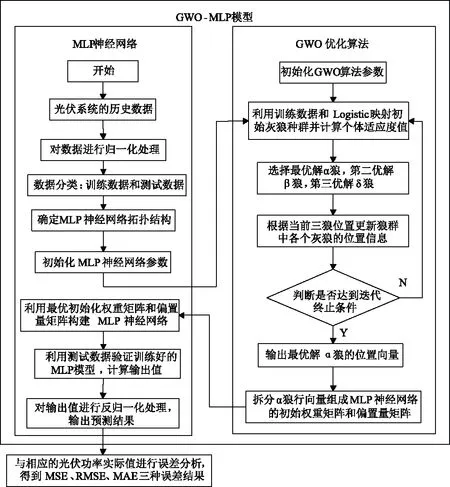
圖2 GWO-MLP模型預測流程圖Fig.2 Flow chart of GWO-MLP model forecast

預測流程如下：

(1)對光伏電站的歷史數據進行歸一化處理；

(16)

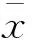
相應地，在MLP神經網絡訓練及測試過程結束后，對輸出值進行反歸一化處理，得到光伏系統功率預測值。反歸一化表達式如下：

(17)

(2)將歸一化后的光伏電站歷史數據按照7：3的比例分為訓練數據和測試數據；

(3)確定MLP神經網絡的拓撲結構；

(4)初始化MLP神經網絡參數；

(5)按照2.2節及2.3節所述方法，使用GWO優化算法優化MLP神經網絡的初始權重矩陣和偏置量矩陣；

(6)運用測試數據驗證訓練好的GWO-MLP模型，計算輸出值；

(7)對輸出值進行反歸一化處理，得到光伏輸出功率預測值，并以MSE、RMSE、MAE作為預測精度評價標準，與相對應的光伏功率真實數據進行誤差結果對比分析。

3.2 模型參數設定

在GWO-MLP模型中，選用光伏電站歷史數據中的溫度、光照強度和風速作為模型的三個輸入量，輸出量為GWO-MLP模型所預測的光伏輸出功率。因此，MLP模型中輸入層和輸出層神經元個數分別設定為3和1；隱藏層的層數設置為2，每層隱藏層包含10個神經元；MLP模型的最大訓練次數設置為1 000，訓練誤差為1e-10，訓練算法為Levenberg-Marquardt算法[18]；GWO的種群數目為10，最大迭代次數為1 000。ELM、 Elman-NN的神經元數目設置與MLP保持一致。SVM的核函數為徑向基核函數，γ設置為0.25。

4 結果分析

為驗證GWO-MLP模型的預測性能，對光伏電站的歷史數據每隔15 min記錄一次，選取1 000組光伏電站的歷史數據，其中每一組數據代表某一時刻光伏電站的實際情況，對選取的1 000組歷史數據進行歸一化處理，隨機選70%數據作為訓練數據，余下數據作為測試數據，1 000組歷史數據如圖3所示。利用MATLAB編程分別建立MLP、Elman、SVM、ELM和GWO-MLP預測模型，并對此5種模型的訓練結果和測試結果進行對比。

圖3 歷史數據Fig.3 Historical data

4.1 訓練結果分析

GWO-MLP 、MLP和Elman-NN三種模型的訓練誤差曲線分別如圖4～圖6所示。由圖4～圖6可以看出，GWO-MLP的訓練誤差最終為9.9e-11，訓練次數為267；Elman-NN的訓練誤差最終為2.35e-5，訓練次數為1 000；MLP的訓練誤差最終為2.01e-10，訓練次數為425。由以上數據對比可得，GWO-MLP的訓練結果和訓練速度均優于Elman-NN和MLP。

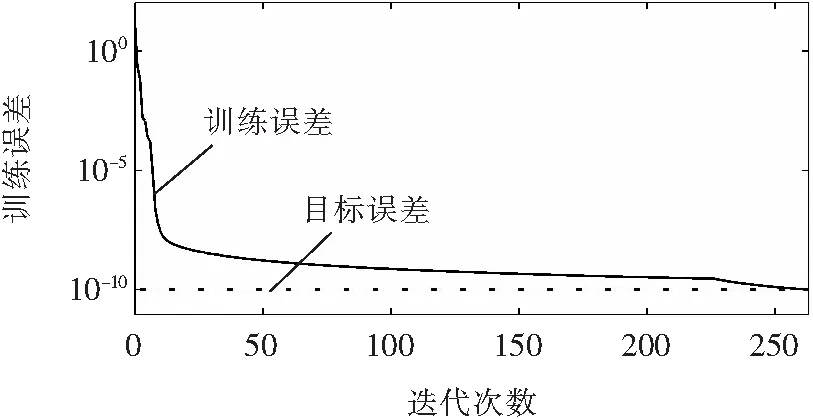
圖4 GWO-MLP的訓練誤差曲線Fig.4 GWO-MLP training error curve

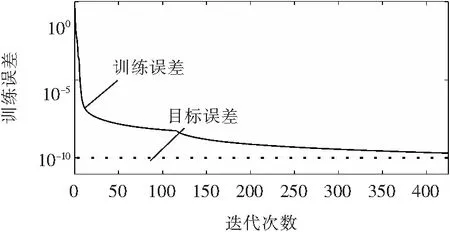
圖5 MLP的訓練誤差曲線Fig.5 MLP training error curve

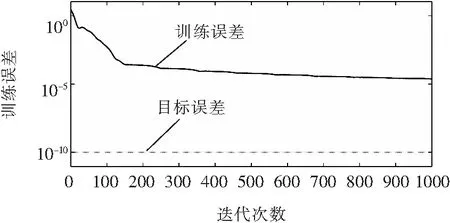
圖6 Elman-NN的訓練誤差曲線Fig.6 Elman-NN training error curve

4.2 測試結果分析

文中選取MSE、RMSE和MAE作為模型的評價標準。

表1為5種模型的預測結果對比。由表1可知，GWO-MLP的MSE為27.102 3，在5種模型中是最低的，與MLP、Elman-NN、SVM和ELM相比，分別降低了7.564 1%、75.463 4%、2.635 4%、33.944 2%；GWO-MLP的RMSE為5.208 3，是5種模型的RMSE中最低的；GWO-MLP的MAE為3.295 4，同樣是5種模型的MAE中最低的。

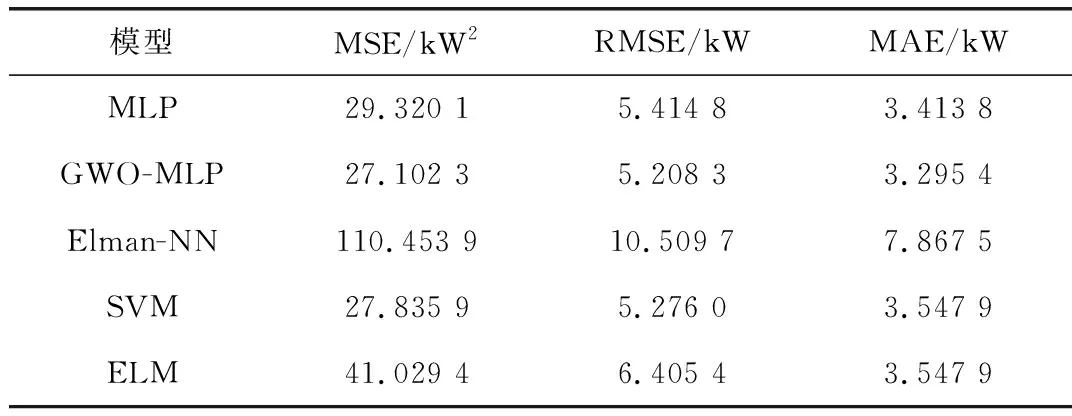
表1 5種模型的預測結果對比Tab.1 Comparison of prediction results of five models

由表1和圖4～圖6可知，在GWO-MLP、MLP、Elman-NN、SVM、ELM這5種模型中，GWO-MLP與MLP的測試效果較為接近，但是由于GWO-MLP模型的初始權重和偏置量是通過GWO給出的，在訓練的尋優速度方面要明顯優于MLP模型；Elman-NN神經網絡與GWO-MLP模型相比，在相同的訓練次數內，Elman-NN神經網絡無法實現預定的目標誤差；SVM的各項指標雖然與GWO-MLP的各項指標接近，但SVM中超參數的選擇十分困難，并且產生的結果不具有規律性，隨機性太強，難以人為把控；將ELM與GWO-MLP進行對比可知，在相同的神經元數目的情況下，ELM的結果比GWO-MLP的結果略差一籌，ELM對光伏系統輸出功率預測的準確性沒有GWO-MLP高。

5 結束語

提出基于GWO-MLP的光伏系統輸出功率短期預測模型，為了減小MLP模型的隨機初始權重和偏置量對光伏系統輸出功率精確度和準確性的影響，將經過混沌理論優化的GWO用于對MLP的初始權重和偏置量進行優化，得到最優的初始權重和最優的偏置量，以此提高MLP的預測速度和預測精度。預測結果表明，與MLP、Elman-NN、SVM、ELM4種模型相比，GWO-MLP在MSE、RMSE、MAE這3種指標上有著更為優秀的表現，在光伏系統輸出功率預測中能夠達到更高的預測精度。根據GWO-MLP預測得到的光伏輸出功率對微網系統的日前調度進行安排是下一步研究工作的重點。