雙饋異步發電機新等效（值）電路及其電力潮流定量分析計算

成健

（東方電氣風電股份有限公司， 四川德陽， 618000）

0 引言

隨著國內風電市場迅速發展和裝機容量逐漸增加， 目前一半以上風電機組采用了雙饋異步發電機， 抽水儲能水力發電機也可采用雙饋異步發電機， 風電/水電與電網的相互影響已不容忽視。搞好雙饋異步發電機電氣方面的基礎性理論研究，對更好地發揮雙饋異步發電機性能優勢具有重要的現實意義。

1 方法綜述

通常， 經過定量分析計算可以確定雙饋異步發電機常規型等效（值）電路上定子端口、 定子支路和轉子端口、 轉子支路的有功功率和無功功率；由于， 其等效（值）電路上激磁支路沒能部分或全部分解為定子側激磁支回路和轉子側激磁支路，所以， 常規型雙饋異步發電機激磁支路中的定子側發電機激磁支回路內電勢、 轉子側激磁支回路發電機內電勢或電動機電勢和相應的有功功率和無功功率， 以及其相互定量關系， 還不能準確定量分析計算出來。

目前， 基于雙饋異步發電機與繞線式異步電機一脈相承的等效（值）電路圖， 按照電路等效原則， 創新地建立了雙饋異步發電機新等效 （值）電路[1]。其中， 基本型雙饋異步發電機等效（值）電路，可以無條件地部分分解其激磁支路； 簡化型雙饋異步發電機等效（值）電路， 在激磁電阻為零的條件下， 也可以把其激磁支路完全分解為定子側激磁支路和轉子側激磁支路。

通過雙饋異步發電機新等效（值）電路及其電力潮流定量分析計算， 可以確定定子側激磁支路發電機內電勢、 轉子側激磁支路發電機內電勢或電動機電勢和相應的有功功率和無功功率， 以及其相互定量關系。

2 雙饋異步發電機常規型等效(值)電路

根據許實章編著《電機學》[2]論述， 變壓器的基本方程式從電路觀點和數學方法2 個方面導出了變壓器的等效（值）電路； 感應電機的基本方程式和變壓器的完全一樣， 只是把變壓器中的負載阻抗改成代表總機械功率的純電阻， 可以直接利用變壓器的“T” 形等效（值）電路， 改成感應電機的“T” 形等效（值）電路。

但是， 上述的感應電機實際上是感應電動機，而不能包括繞線式感應發電機， 即雙饋異步發電機。 由于雙饋異步發電機結構與繞線型感應電動機相似， 定子、 轉子均為三相對稱繞組， 磁路、電路對稱、 均勻[3]； 因此， 雙饋異步發電機與繞線式異步電機的 “T” 形等效（值）電路圖是一致的。不同的是： 在雙饋異步發電機超同步運行時轉子端口輸出有功功率， 在次同步運行時轉子端口輸入有功功率， 同步運行時轉子端口只是輸入少許有功功率， 其值等于轉子支路銅損有功功率和轉子側激磁支路鐵損有功功率； 而雙饋異步發電機定子端口在超同步運行、 次同步運行、 同步運行時始終是輸出有功功率。

2.1 雙饋異步發電機常規型等效(值)電路轉子回路參數折算

雙饋異步發電機常規型等效（值）電路的參數等效變換。

第一步先把雙饋異步發電機轉子繞組頻率f2折算到定子繞組頻率f1， 稱為 “頻率折算”， 其折算值是把原來轉子回路各物理量的符號 “s” 除掉后來表示。 第二步再把雙饋異步發電機轉子繞組折算到定子繞組， 稱為“繞組折算”， 其折算值是用原來轉子回路各物理量符號加上一個 “＇” 來表示。

圖1 是常規型雙饋異步發電機 “繞組折算”和“頻率折算” 后的等效（值）電路。

圖1 常規雙饋異步發電機等效（值）電路

依據圖1， 可以列出式（1）：

定子回路由定子端口、 定子支路、 激磁支路定子側組成； 轉子回路由轉子端口、 轉子支路、激磁支路轉子側組成。 雙饋異步發電機常規型等效（值）電路的激磁支路定子側與激磁支路轉子側是完全耦合一起的。

雙饋異步發電機常規型等效 （值） 電路式（1）中， 假設雙饋異步發電機常規型等效（值）電路激磁支路上有A、 B、 C 3 點。

2.2 雙饋異步發電機常規型等效（值）電路激磁支路等效轉換存在的問題

上述雙饋異步發電機常規型等效（值）電路實際上是一個有源兩端口電路， 即激磁支路是有源回路。 雙饋異步發電機在超同步運行時， 其激磁支路對于定子端口是發電機內電勢， 對于轉子端口是發電機內電勢； 在次同步運行時， 其激磁支路對于定子端口是發電機內電勢， 對于轉子端口是電動機電勢。 由于雙饋異步發電機常規型等效（值） 電路中激磁支路， 沒有考慮定子側激磁支路發電機內電勢和轉子側激磁支路的發電機內電勢或電動機電勢； 因此， 雙饋異步發電機激磁支路定子側和轉子側都存在相互關聯的感應電勢， 在等效轉換過程中不能只用電壓降和激磁電抗表示，應該至少是定子側激磁支路既有電壓降和又有發電機內電勢， 轉子側激磁支路既有電壓降和又有發電機內電勢或電動機電勢。 根據發電機原理，雙饋異步發電機常規型等效（值）電路的定子回路電流、 有功功率流向由激磁支路指向定子端口，根據電動機原理， 雙饋異步發電機常規型等效（值） 電路的轉子回路電流、 有功功率流向由轉子端口指向激磁支路。

3 雙饋異步發電機新等效（值）電路

雙饋異步發電機新等效（值）電路分為基本型、簡化型。

3.1 雙饋異步發電機基本型等效（值）電路

依據式（1）可以推導得出式（2）， 建立雙饋異步發電機基本型等效（值）電路（轉子回路參數是經過“繞組折算” 和“頻率折算” 后得到的）； 并得到圖2， 其中， 定子側激磁支路的激磁電抗為xm，轉子側激磁支路的激磁電抗為xm。 另外， 定子回路A 點與轉子回路A 點之間同電位但沒有電流，等效（值） 電路圖2 中的激磁支路A 點至B 點， 初步實現激磁支路的部分分解。

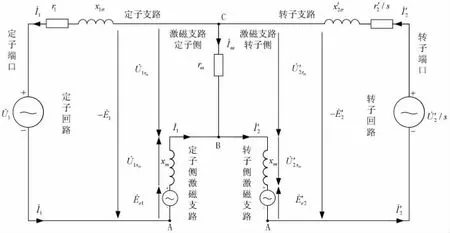
圖2 基本型新雙饋異步電機等效（值）電路

3.2 雙饋異步發電機簡化型等效（值）電路

假設圖2 中的激磁支路激磁電阻為rm=0 時，圖2 變成圖3， 并可得公式（3）。 這樣就實現等效（值）電路圖1 激磁支路從A 點至B 點以及C 點完全分開， 即有條件實現其激磁支路分解為無耦合的定子側激磁支路和轉子側激磁支路。

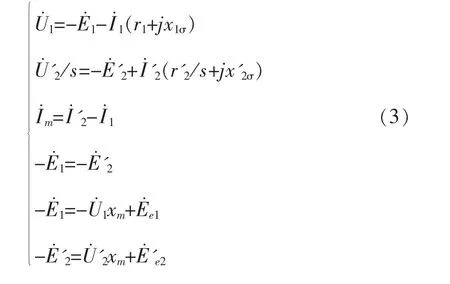
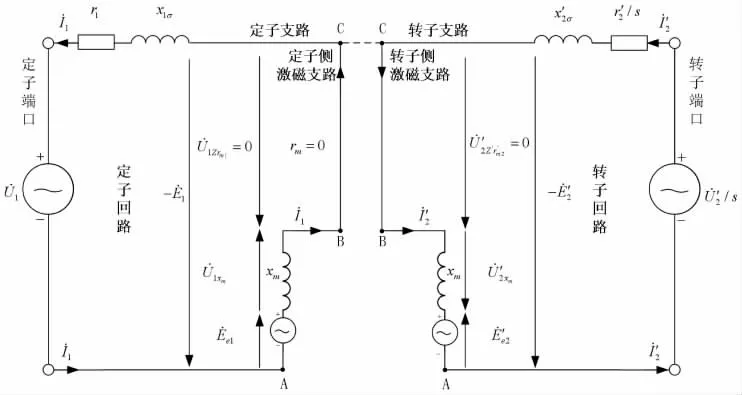
圖3 簡化型新雙饋異步等效（值）電路

4 雙饋異步發電機新等效(值)電路電力潮流計算

雙饋異步發電機定子支路相數m1與轉子支路相數m2相等且為3 相的情況下， 電機電勢變比kc與電流的變比ki相等， 且 “繞組折算” 后， 轉子支路電壓變化量與電流的變化量正好成反比； 也可以這樣講， “繞組折算” 前后， 發電機轉子支路的功率（包括視在容量、 有功功率、 無功功率）不變。

為了便于雙饋異步發電機新等效（值）電路電力潮流計算結果的一致性， 同時又要能保證雙饋風電/水電機組實際輸入機械有功功率、 雙饋異步發電機定子氣隙磁場的有功功率、 無功功率和轉子氣隙磁場的有功功率、 無功功率在圖中得到完整體現， 因此在雙饋異步發電機氣隙磁場與雙饋異步發電機新等效（值）電路的轉子側激磁支路之間引入 “頻率折算” 變換 “-1／s”。 其中， 雙饋異步發電機新等效（值）電路轉子回路參數是在經過“頻率折算” 和“繞組折算” 后計算而得； 而雙饋風電/水電發電機組輸入機械有功功率后， 得到氣隙磁場有功功率， 再由滑差變成定子氣隙磁場的有功功率和轉子氣隙磁場的有功功率 （其與經過“繞組折算” 的轉子氣隙磁場的有功功率相等），然后經過引入等效的 “頻率折算” 變換 “-1／s”后， 它就可以與經過“頻率折算” 和 “繞組折算”后的雙饋異步發電機新等效（值）電路中的轉子回路的氣隙磁場有功功率無差別對接； 而氣隙磁場無功功率， 由滑差變成定子氣隙磁場的無功功率和轉子氣隙磁場的無功功率 （其與經過 “繞組折算” 的轉子氣隙磁場的無功功率相等）， 然后它經過引入等效的 “頻率折算” 變換 “-1／s” 后， 就可以與經過 “頻率折算” 和 “繞組折算” 后的雙饋異步發電機新等效（值）電路中的轉子回路的氣隙磁場無功功率無差別對接。

4.1 雙饋異步發電機基本型等效（值）電路電力潮流計算

雙饋異步發電機基本型等效（值）電路和相應電力潮流定量分析計算， 可以確定通過雙饋異步發電機轉動軸上的轉子繞組與定子繞組之間的氣隙磁場， 風力或水力輸入風電/水電機組機械有功功率Pmec轉換成三相電路中每相的氣隙磁場有功功率Pe后， 又實時轉換成每相定子氣隙磁場有功功率Pe1和每相轉子氣隙磁場有功功率Pe2s（P'e2s）或“頻率折算” 變換 “-1／s” 后為P'e2， 即Pe2s＝P'e2s＝－sPe1。

4.1.1 定子回路

4.1.2 轉子回路

因此， 根據以上推導， 可得雙饋異步發電機基本型等效（值）電路電力潮流計算公式（4）和圖4。

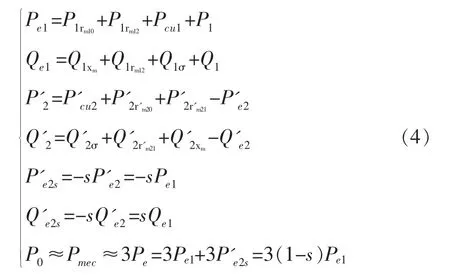
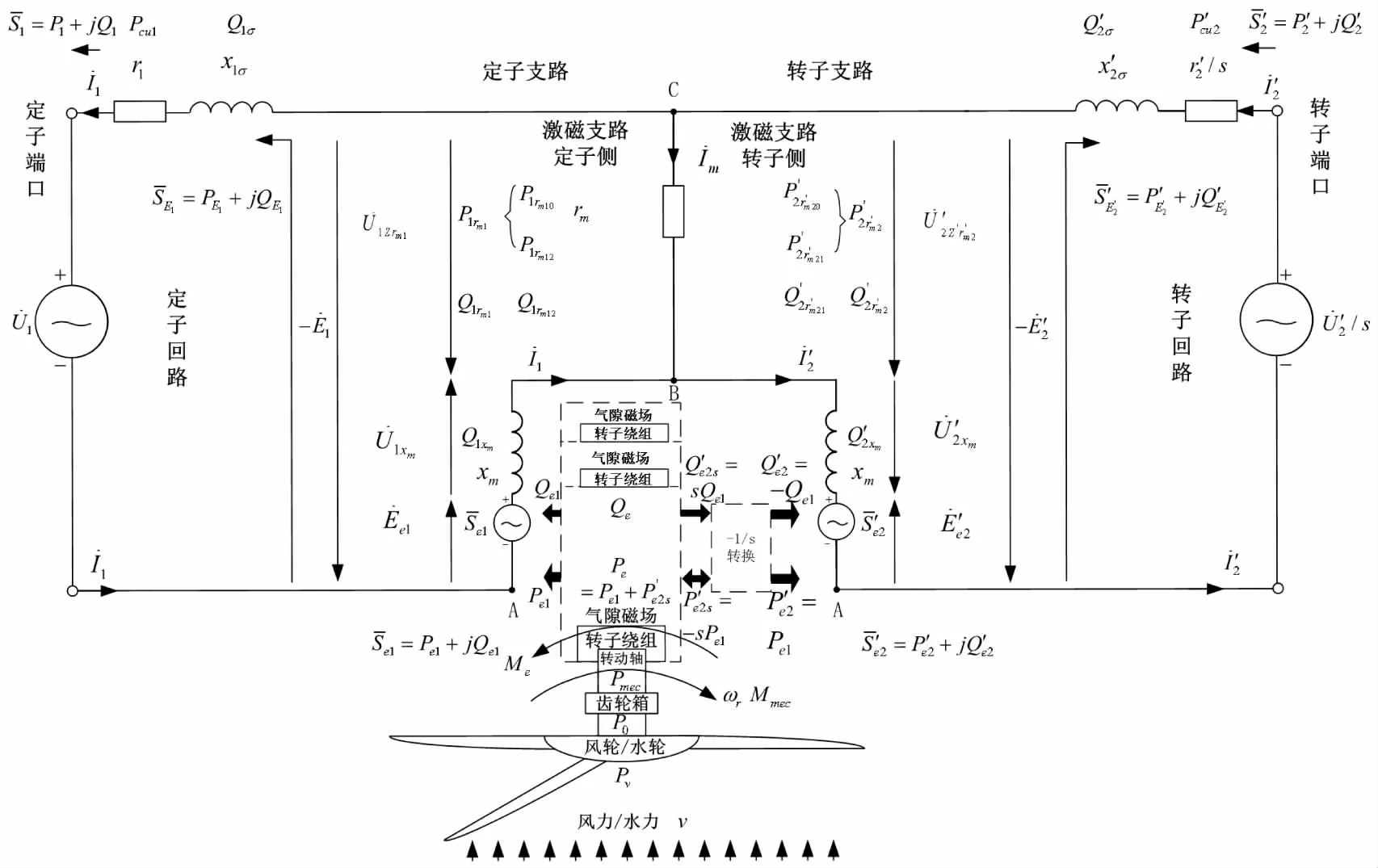
圖4 基本型新雙饋異步發電機等效（值）電路及其功率潮流定量分析計算

4.2 雙饋異步發電機簡化型等效(值)電路及其電力潮流計算

雙饋異步發電機簡化型等效（值）電路是雙饋異步發電機基本型等效（值）電路特例， 即rm=0，因此可得， P1rm10=0， =P1rm120， P'2r'm20=0， P'2r'm21=0； Q1rm12=0， Q'2r'm21=0； 由公式（4）簡化后， 可得雙饋異步發電機簡化型等效（值）電路電力潮流計算公式（5）和圖5。

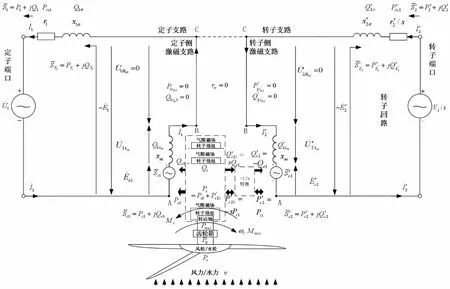
圖5 簡化型新雙饋異步發電機等效（值）電路及其功率潮流定量分析計算

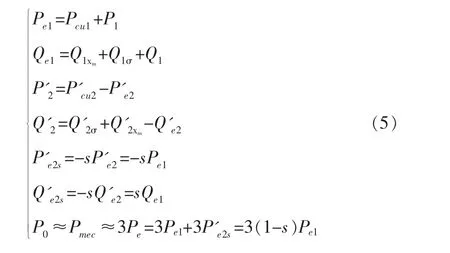
5 小結

通過上面所述， 創新地建立了雙饋異步發電機新等效（值）電路[1]。 雙饋異步發電機基本型等效（值） 電路， 可以無條件地部分分解其激磁支路；雙饋異步發電機簡化型等效（值）電路， 在激磁電阻為零的條件下， 也可以把其激磁支路完全分解為定子側激磁支路和轉子側激磁支路。 通過雙饋異步發電機新等效(值) 電路及其電力潮流定量分析計算， 可以確定定子側激磁支路發電機內電勢、轉子側激磁支路發電機內電勢或電動機電勢和相應的有功功率和無功功率， 以及其相互定量關系；尤其是可以確定三相定子側激磁支路發電機內電勢產生的氣隙磁場有功功率與三相轉子側激磁支路發電機內電勢或電動機電勢產生的氣隙磁場有功功率之和等于風能輸入的機械有功功率關系。

而且， 可以完整地做出雙饋風電/水電機組運行輸入機械功率和雙饋異步發電機等效 （值） 電路及其電力潮流定量分析計算。 通過應用雙饋異步發電機新等效(值) 電路， 我們在實際工程應用中， 可以更好地理解風電/水電機組雙饋異步發電機定子發電輸出功率和轉子發電輸出或受電輸入功率的運行原理。