空化螺旋槳噪聲特性的研究

齊天成，吳思源，張懷新

（1.上海交通大學 海洋工程國家重點實驗室，上海200240；2.高新船舶與深海開發裝備協同創新中心，上海200240）

0 引言

伴隨著船舶大型化和高速化的發展，螺旋槳的負荷與轉速相應提高。當螺旋槳槳葉表面某處的壓力低于水的飽和蒸汽壓力時，水汽通過界面，進入氣核并使之膨脹，形成氣泡，稱為空泡[1]。螺旋槳槳葉表面空泡的產生和消失引起的壓力變化是引發螺旋槳空泡噪聲的重要原因[2]，且空泡噪聲作為船舶輻射噪聲的重要組成部分，嚴重影響到船員的舒適性和艦艇的隱蔽性。螺旋槳的空泡和噪聲特性始終受到眾多研究者的關注。

隨著計算流體力學的不斷發展，利用數值計算的方法模擬螺旋槳空泡現象并預報空泡噪聲已經得到了廣泛的應用。吳崇建等[3]基于等效聲源法探究了螺旋槳“水母模態”被激發時誘導出的低頻窄帶聲輻射特性。朱江波等[4]在驗證螺旋槳敞水水動力性能的基礎上，運用聲學軟件Actran分析了螺旋槳的無空泡噪聲特性。張成等[5]通過大渦模擬求解螺旋槳流場壓力信息，利用Light-Hill聲類比理論計算了研究域的噪聲分布情況。侯知音等[6]使用Fluent計算了CRP-7對轉槳在均勻來流下的瞬態水動力性能，并利用Fluent的聲學仿真模塊對無空泡線譜噪聲進行了數值模擬分析。王順杰等[7]采用動網格模型對對轉槳進行了空化數值分析，并基于FW-H方程探究了空泡噪聲聲壓脈動特性和聲壓功率譜特性。姚慧嵐[8]等以槳葉表面脈動壓力為聲源，對螺旋槳的低頻離散線譜噪聲、低頻寬帶噪聲和高頻渦流噪聲進行了預報分析。Savas Sezen等[9-10]結合雷諾時均N-S方程和FW-H方程，研究了非空化和空化條件下船用螺旋槳的噪聲譜以及螺旋槳葉片數量對噪聲譜的影響。Bal Sakir等[11]采用Brown方程計算了空化螺旋槳的噪聲譜和總聲壓級，并討論了螺旋槳側斜角對噪聲的影響。

將基于德國波茨坦水池在2011年組織的螺旋槳空泡研討會上選用的算例螺旋槳PPTC螺旋槳，利用StarCCM+軟件計算得到其在均勻來流下的空泡性能，將得到槳葉表面的脈動壓力后導入聲學軟件Virtual.Lab Acoustics中，運用邊界元方法（BEM）計算螺旋槳的空化噪聲特性。通過建立準確可靠的數值模擬計算方法，為相關研究提供參考。

1 流場計算

1.1 數值方法

連續性方程是質量守恒定律在流體力學中的表現形式，而在空泡發生時，空間中存在著氣液兩相，因此基于均質混合流的連續性方程如下：

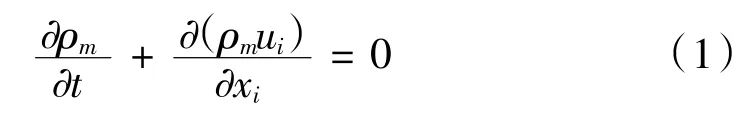
式中：ρm為混合密度，即ρm=ρ（l1-α）+ρvα，ρl和ρv分別是液相和氣相的密度，α是氣相的體積分數。動量方程為：

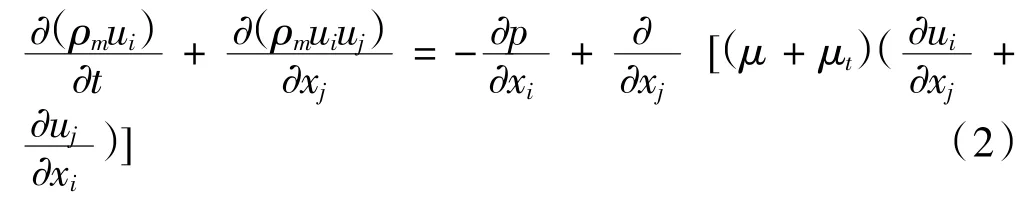
式中：μ為混合動力黏性系數；μt為湍流引起的混合渦流黏性系數，需要通過求解湍流模型得到。

空泡模型選擇StarCCM+軟件中內置的Schnerr&Sauer模型，該模型是基于質量輸運方程的多相流模型，輸運方程由下式表示：

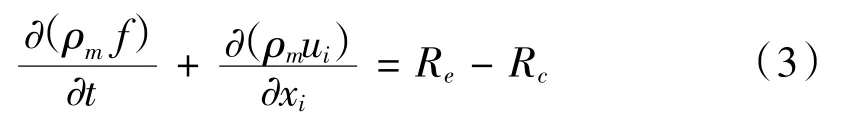
式中：f為蒸汽的質量分數，與體積分數α的關系：f=，Re、Rc為源項汽化率和冷凝率，由Schnerr&Sauer模型計算。

1.2 計算模型

本研究選定的研究對象PPTC螺旋槳是型號為VP1304的可調螺距螺旋槳，在2011年德國召開的船舶推進器國際研討會上以此槳展開了豐富的試驗和數值計算研究，并公布了用以驗證數值計算方法的相關試驗結果。槳的主要參數為：直徑為0.25 m，葉數為5，轂徑比為0.3，盤面比為0.77896，側斜角為18.837°，0.7R螺距比為1.635，選擇方向右旋。

對均勻流場下螺旋槳的空化模擬，首先建立相應的計算域。考慮螺旋槳的運動模式是周期性的旋轉運動，因此整個計算域由旋轉域和靜止域兩部分組成。計算域的具體設置見圖1。本研究對計算域的網格劃分采用切割體網格，設置槳葉壁和第一層網格的Y+值高于30，并對葉梢部分網格的進一步加密。經網格無關性驗證，綜合考慮計算成本、計算精度，選取了一套疏密程度合理的網格，總單元為286萬個。

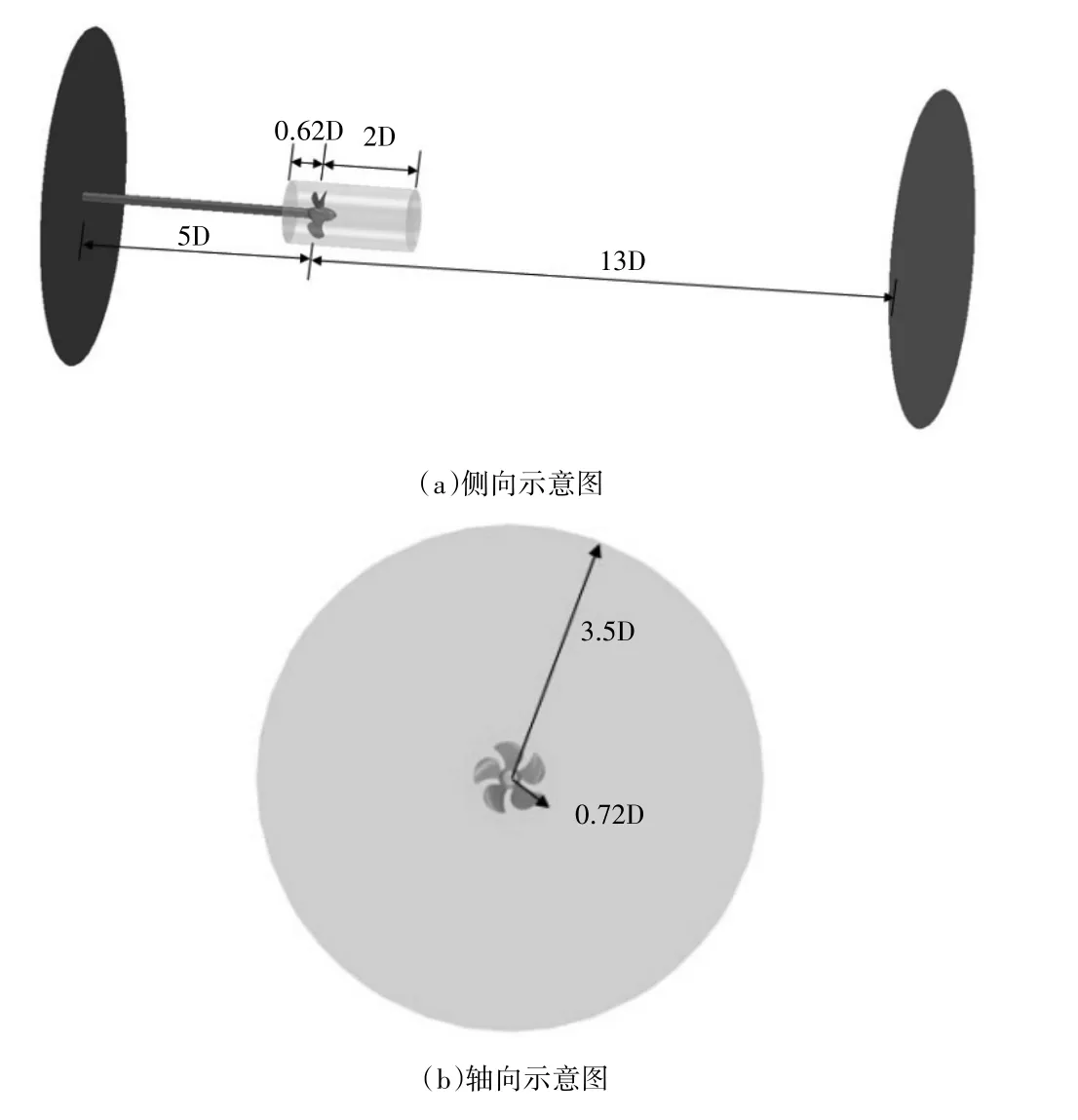
圖1 流場計算域示意圖

1.3 螺旋槳空泡性能計算結果

螺旋槳的空泡現象會產生一系列危害，比如導致螺旋槳的水動力性能惡化，槳葉表面材料的剝蝕等，甚至會致使諧鳴并誘導船舶的尾振。因此，對螺旋槳的空泡性能預報具有重要意義[12]。基于課題組已做出的相關研究，本節將螺旋槳空泡性能的數值模擬結果與現有的螺旋槳模型的空泡性能試驗數據進行對比，驗證模擬空泡的數值模擬方法的準確性，并給出空泡分布隨空泡數變化的規律，為下一小節中對螺旋槳空泡噪聲的預報提供基礎。

德國漢堡舉辦的船舶推進器國際研討會上對PPTC螺旋槳在3種工況下的空泡性能進行了試驗與觀測[13-14]，選取其中的Test case2.3.1工況進行數值計算和分析，具體參數為：進速系數J=1.019，密度ρ=997.44 kg/m3，運動黏性系數ν=9.337×10-7m2/s，飽和蒸汽壓力pv=2818 Pa，螺旋槳轉速n=255 s-1。σ為空泡數，定義為，其中，p0為遠場環境壓力，根據給定的σn和pv，可推算出p0，并將其作為計算域出口壓力值。對于空泡性能的模擬采用非定常計算，時間步長設置為5×10-4s，最大物理時間為0.2 s。在已設置的物理時間內，計算已經收斂。

在不同空泡數下的螺旋槳推力系數和扭矩系數的數值計算結果與試驗結果的對比如圖2所示。

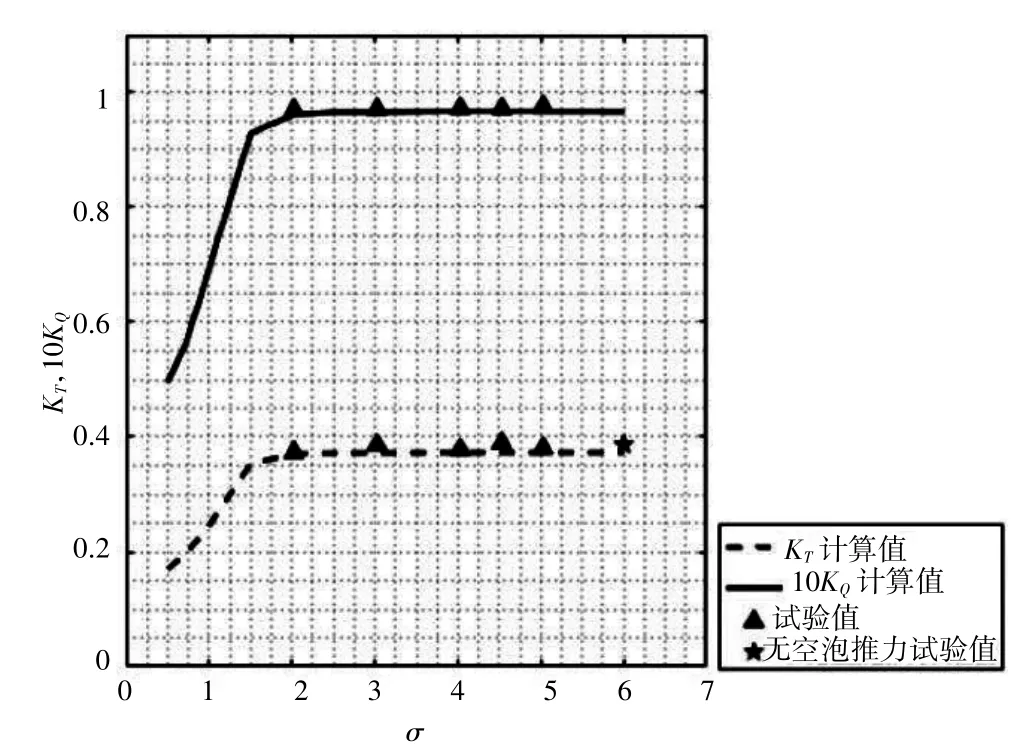
圖2 PPTC螺旋槳空泡性能曲線

從圖2可以看到，數值計算所得的推力和扭矩系數與試驗數據非常相近，驗證了數值模擬的可靠性。當空泡數高于2時，螺旋槳的推力和轉矩基本保持不變；當空泡數低于2時，螺旋槳的推力和轉矩線性減小，其水動力性能發生了急劇惡化。

圖3顯示出幾個典型空泡數對應的槳葉吸力面上的空泡分布情況：高空泡數時并未產生空泡，隨著空泡數的減小，空泡開始從導邊出現，并逐漸發展至葉梢，在葉根處也逐漸出現片空泡。隨著空泡數的進一步減小，空泡開始從導邊向槳葉面的內部延展，直至隨邊，最終將整個葉面基本覆蓋。

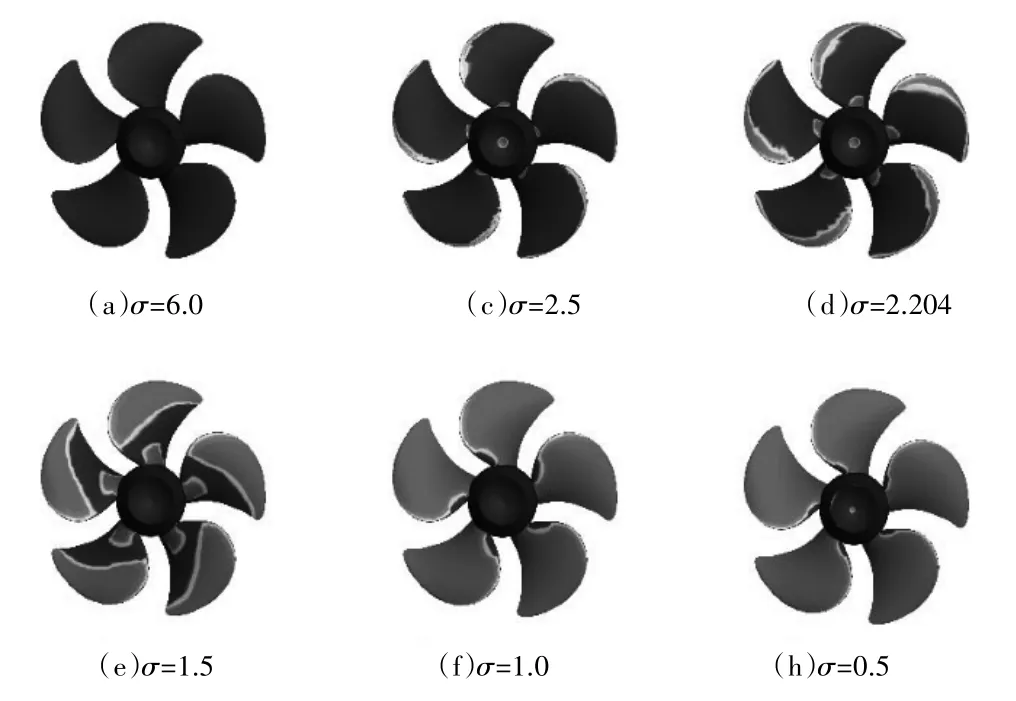
圖3 PPTC槳葉面空泡分布隨空泡數變化示意圖

本節依據的黏性流的多相流理論，所采用的計算模型和方法可以有效地預報螺旋槳的空泡性能，從而為下一小節的空泡噪聲預報提供參考。

2 聲場計算

2.1 數值方法

聲輻射的本質是流體邊界壓力脈動對聲場點的介質壓力傳導[12]，本研究對聲輻射的計算采用間接邊界元方法。將流場計算得到的壓力脈動偶極子數據作為螺旋槳噪聲輻射的聲源。邊界元方法與有限元方法不同的是，邊界元方法將三維求解域上的離散轉換為二維求解域邊界上的離散，數值計算僅僅在邊界上進行，優勢在于不需要求解區域內的未知量，從而可以大量減少未知量的個數以及需要求解的方程數，非常適合于求解聲學問題。

結構外部聲場的Helmholtz積分方程為：

式中：p（X）為聲場中任一點的聲壓；p（Y）為聲源點的聲壓；α（X）為曲面光滑系數；vn（Y）為聲源邊界與媒介交界處的法向速度；G（X，Y）為自由空間的格林函數。

2.2 聲場網格劃分與聲壓監測點設置

本節在聲學分析軟件Virtual.Lab中通過間接邊界元法，將StarCCM+中瞬態計算所得的槳葉表面的壓力數據作為偶極子聲源，對螺旋槳發生空泡時的噪聲特性進行計算分析。

為通過邊界元法計算螺旋槳周圍的聲場，需要重新對聲場網格進行劃分。與流場網格的劃分不同，聲場網格的劃分無需在一些區域進行加密處理，應盡量保持一致的均勻性，并且過密的網格對于提升計算精度并無幫助，因此只需在變化率較大的曲面邊界上細化網格。在ICEM軟件中對聲場網格進行劃分，如下圖4所示。由于螺旋槳表面在幾何上的復雜性，因此選用適應性較佳的三角形面網格，槳轂表面與槳葉的網格尺寸基本保持一致，網格單元共計26641個。

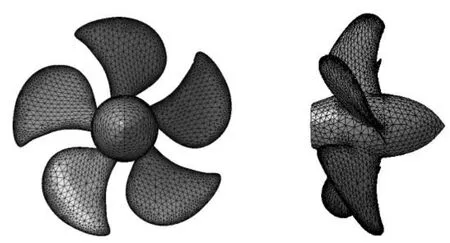
圖4 聲學網格

將聲壓監測點分別設在螺旋槳的軸向和縱向上，以探討螺旋槳流噪聲在空間和頻域的分布特征。軸向監測點與槳盤面中心距離為D（D為螺旋槳直徑），徑向監測點與槳盤面中心距離為0.5D。兩個聲壓云圖的平面相互垂直，均為邊長8D的正方形，記為橫剖面1和縱剖面2，橫剖面的法向與螺旋槳軸向相同，如上圖5所示。

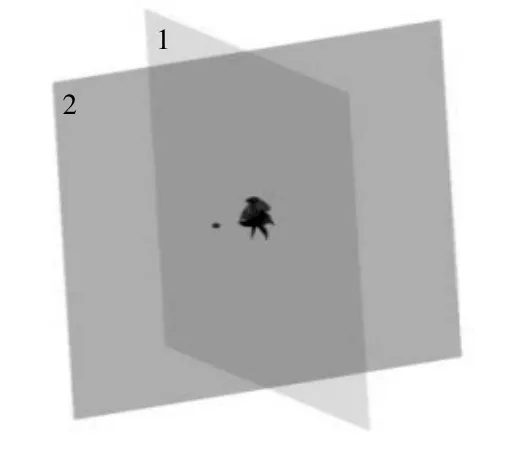
圖5 聲壓監測點、面

2.3 噪聲計算結果分析

在給定工況下對空泡噪聲的計算進行分析。噪聲計算所支持的最大頻率和流場計算的時間步長有關，即。考慮到本次噪聲特性的分析頻率范圍在1500 Hz以內，取時間步長為1×10-4。

圖6給出了在不同空泡數下，軸向與徑向上的聲壓監測點處的頻域分布曲線。可以發現，空泡數σ=2.024的聲壓級最高，然后是空泡數σ=1，而空泡數σ=6的聲壓級最低。對比圖3中的空泡分布形態進行分析：空泡的產生加劇了螺旋槳的噪聲，即加劇了在槳葉表面上的脈動壓力成分，所以圖6中的實線曲線在灰色曲線的上方。而虛線曲線在實線曲線的上方，這是由于在空泡數σ=1時，空泡基本將槳葉表面整體覆蓋，從而形成超空泡流動，槳葉表面主要與氣相接觸，空泡形態相對穩定，槳葉表面的脈動壓力不是很劇烈，但空泡數σ=2.024時空泡主要產生于槳葉葉梢與轂部，穩定性變差，該工況在數值模擬中存在空泡范圍的波動，進而致使槳葉表面的脈動壓力成分加劇，噪聲因此也最大。相關研究也指出，在空泡初始狀態下相較于較強空泡狀態下，螺旋槳的噪聲要更大。

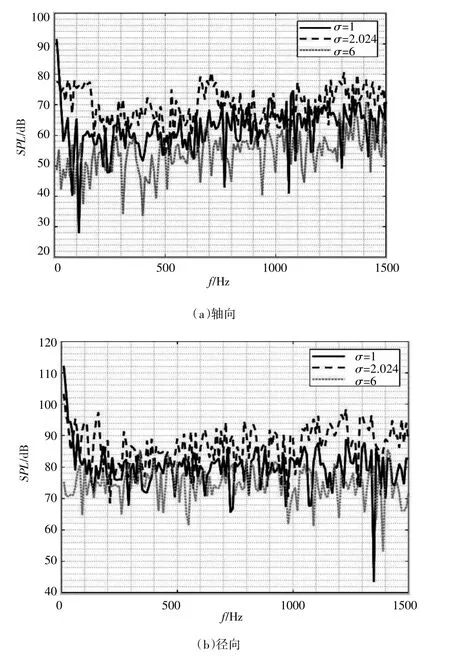
圖6 聲壓監測點不同空泡數下頻譜曲線比較

圖7給出了空泡數為2.024時，在軸頻附近的30 Hz，2倍軸頻50 Hz，葉頻附近的120 Hz，4倍和10倍葉頻下橫剖面1的螺旋槳聲壓云圖。

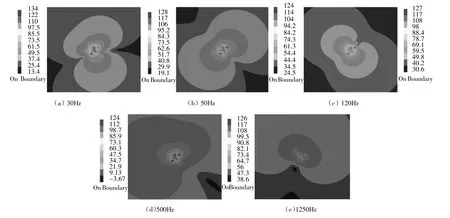
圖7 聲場橫剖面聲壓云圖（2.024）

從圖7可以發現，距離聲源越近，噪聲的聲壓級越高，隨著距離聲源漸遠，噪聲的聲壓級逐漸降低。對于以上選取的幾個頻率點，其聲壓級相較于周圍頻率處的都要更高。例如在空泡數σ=2.024時，低頻區域：30 Hz的中心聲壓級達到134 dB，在2倍軸頻50 Hz的中心聲壓級達到128 dB，而在周圍頻率40 Hz與60 Hz下的中心聲壓級僅有118 dB，124 dB。中頻區域：在4倍葉頻500Hz處的中心聲壓級為124 dB，周圍頻率520 Hz處的中心聲壓級為121 dB。高頻區域：10倍葉頻1250 Hz處的中心聲壓級達到139 dB，而在周圍頻率1220 Hz處的中心聲壓僅為134 dB。因此可以得出，槳葉表面脈動壓力的葉頻、倍葉頻、軸頻、倍軸頻的分量作用明顯。

聲壓云圖還顯示出了螺旋槳流噪聲的傳播特性，其輻射具有顯著的指向性。在不同的頻率下，聲壓云圖的分布特性表現出了一定差異。在低頻區（＜300 Hz），螺旋槳作為聲源表現出典型的偶極子聲源特征，其輻射形態為傾斜的“8”型，在中高頻區（＞500 Hz）聲壓云圖并未表現出明顯的規律，總體上呈放射形態的分布。在相同頻率下，空泡數的不同也會影響到聲壓云圖的分布特性。

同樣地，圖8給出在空泡數為2.024時，在軸頻附近的30 Hz，2倍軸頻50 Hz，葉頻附近的120 Hz，4倍和10倍葉頻下縱剖面上的螺旋槳聲壓云圖。

在聲場縱剖面上，螺旋槳噪聲聲壓級在中心處最高，在四周方向上呈下降的趨勢，在空泡數對噪聲的影響方面，也表現出與橫剖面上近似的規律。噪聲的傳播同樣表現出了顯著的指向性，但與橫剖面上的噪聲輻射特征又有所差異：在低頻及中頻區（＜750 Hz），聲場的輻射形態表現為水平倒放的“8”型，在0°與180°方向上的聲壓級較高，即對于距離槳盤面中心相等的位置，軸向的聲壓級要高于徑向的聲壓級；高頻區的聲壓分布并未顯現出明顯規律，聲壓分布總體上為放射態。空泡在一定程度上會改變噪聲的輻射形態，因此，即便在相同的頻率下，聲壓云圖的分布也會由于空泡數的不同而存在差異。

綜上，利用Virtual.Lab計算中的邊界元方法，在計算螺旋槳空泡流場的基礎之上，探究了空泡噪聲的頻域和空間分布特征，為預報螺旋槳噪聲提供了新思路。

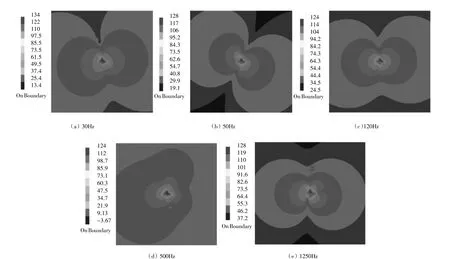
圖8 聲場縱剖面聲壓云圖（2.024）

3 結論

通過計算流體力學和聲場邊界元的方法以PPTC螺旋槳為研究對象，探究了其空化螺旋槳的噪聲特性，在Star-CCM+軟件中選用Schnerr&Sauer空泡模型，對螺旋槳的空泡性能進行計算，得到不同空泡數下的螺旋槳推力及扭矩系數，與試驗結果相比非常準確，并得到空泡數變化下的空泡分布形態發展。在空泡計算結果的基礎上，利用Virtual.Lab Acoustics軟件，采用邊界元方法計算了螺旋槳在軸向和徑向的空泡噪聲聲壓頻譜，頻譜曲線中良好地體現了螺旋槳的軸頻和葉頻信息；空泡的產生會增大螺旋槳噪聲，受到不同程度空泡形態的影響，頻譜曲線的分布趨勢不同；對于螺旋槳聲壓云圖的分析表明，螺旋槳作為面聲源，顯示出了典型的偶極子聲源特性，聲場的輻射特性呈“8”型，低頻聲壓和高頻聲壓分布規律存在差異性。