相干信源的DOA空間譜估計研究
李君惠 楊志強 華 雷
(四川九洲空管科技有限責任公司 四川綿陽 621000)
0 引言
陣列信號處理中的一個重要且常用的領域就是DOA空間譜估計,想要對目標進行超分辨測向,必須計算出信號的空間譜。在實際空間環境中,由于反射遮擋等因素造成了多徑干擾,因此存在大量的相干信源。當要進行DOA的信源完全相干的時候,接收數據的協方差矩陣的秩降為一,DOA的信源數就要大于DOA子空間,因此,傳統的DOA算法,如MUSIC算法,不能對相干信號源進行分辨測向。DOA算法對相干信源的超分辨測向一直具有研究意義。
1 MUSIC算法原理以及仿真分析
1.1 MUSIC算法原理
當接收信號為窄帶時,天線陣列傳播期間接收到的信號的包絡可以認為是恒定的。陣列天線為線陣時,天線陣列和信源為同一平面內,陣元間距為,接收的信號數目為,信源方向(=1,2,…,)入射根天線,如圖1所示。
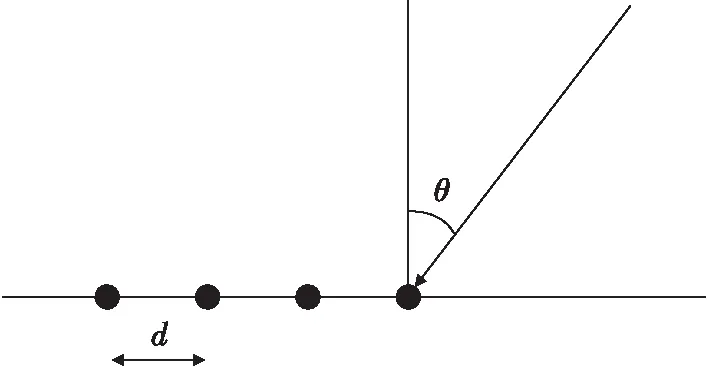
圖1 均勻線陣
入射信號向量()為
()=((),(),…())
(1)
線陣響應矢量為
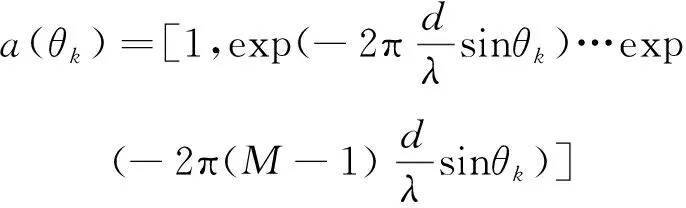
(2)
方向矩陣為
=[(),(),…,()]
(3)
接收到信號為
()=()()+…()()
(4)
實際中存在噪聲,陣列接收信號為
()=()+()
(5)
式(5)中,()表示為白噪聲向量;()表示為空間信號向量;()表示為接收數據向量;表示為方向矩陣。接收信號的空間相關矩陣可為
=[()()]=+
(6)
對式(6)中的進行特征值分解,其中,,…,為特征值,由此,,…,是對應的特征向量。其中與信號有關的特征值為,,…,,剩下的是與噪聲有關的-特征值,綜上可以定義噪聲子空間表示為
=[+1,+2,…,]
由此,MUSIC的譜估計為
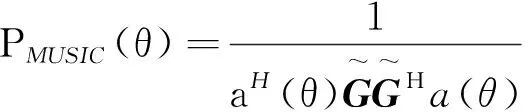
(7)
式(7)中,信號入射方向也就是MUSIC譜函數中的第個峰值相應的位置。
1.2 MUSIC算法仿真分析
利用Matlab仿真軟件產生3路信源,并仿真MUSIC算法,仿真參數如表1所示。

表1 實驗條件
在表1的條件下,用Matlab仿真給出了MUSIC測向結果,如圖2所示。
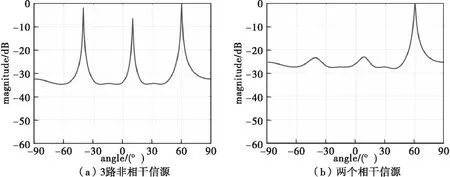
圖2 MUSIC算法仿真
圖2(a)仿真采用3路非相干信源,圖2(b)仿真采用兩個相干信源,方向為-40°和方向為10°。圖2的仿真結果可得出結論,MUSIC算法可以有效地對非相干信源進行測向,當信源為相干信源時,MUSIC算法失效。
2 相干算法原理及仿真分析
在處理強相干信源的方法中,主要分為兩種:第一種方法采用非降維處理;第二方法采用降維處理。在這些方法中,空間平滑、矢量奇異值類、矩陣分解為降維處理算法;Toeplitz算法、改進MUSIC算法為非降維處理算法。
2.1 空間平滑SS-MUSIC算法原理
為解決相干信源的超分辨測向,提出了只適合于均勻線陣的空間平滑算法(SS-MUSIC)算法。SS-MUSIC算法為了恢復數據協方差矩陣,采用子陣平滑的方法,算法分為:
1)前向平滑MUSIC算法(FSS);
2)后向平滑MUSIC算法(BSS);
3)修正的空間平滑MUSIC算法(MSS)。
空間平滑技術是對付強相關信號的有效方法,其算法原理是將均勻線陣(陣元)分成個相互重疊的子陣,其中每一個子陣的陣元數為,因此=+-1,為恢復滿秩協方差矩陣,需要求得各子陣協方差矩陣的均值。當相干信源數大于子陣的陣元數目時,前后向平滑數據協方差矩陣均是滿秩矩陣。修正的空間平滑算法的實質對前后向平滑矩陣的平均。經過分析可知,FSS算法和BSS算法相比于MSS算法具有更大的孔徑損失,同時FSS算法和BSS算法可分辨的信源數相較于MSS算法更少,因此本文只仿真MSS算法。
2.2 改進空間平滑ISS-MUSIC算法原理
在前述基礎上進一步做相應的互相關處理,最后對處理后的數據進行加和平均,即得到其等效的空間平滑矩陣。在文獻[6]中,作者改進了平滑空間算法,ISS-MUSIC算法首先對信號的協方差矩陣進行修正,然后根據修正后的空間平滑矩陣做波達方向估計計算,ISS-MUSIC算法具有更好的分辨力。
2.3 Toeplitz算法
陣列接收的數據在理想情況下,其協方差矩陣具有Toeplitz性質,然而在實際情況下,接收到的數據會受到誤差的影響,尤其是信噪比很低的時候,接收數據的的協方差矩陣通常為對角占優的矩陣。因此要想得到接近真實的數據協方差矩陣可通過對其進行Toeplitz預處理。
Toeplitz算法與矩陣分解算法、空間平滑算法以及矢量重構算法不同,因為該算法的解相干的性能是通過改變協方差矩陣的數據結構獲得的,不是由降低自由度而獲得,因此,Toeplitz算法具有相對更高的陣列的孔徑利用率。由于信號的先驗信息沒有在算法的數據重構中得到反應,故而當信號源功率不同時,算法的DOA估計精度就會相對不理想,以上分析會在其后的仿真中進一步展示說明。
2.4 矢量奇異值VSV-MUSIC算法
矢量奇異值算法基于定理:陣列接收的數據協方差矩陣特征值分解后,其特征值對應的特征矢量為各信號源導向矢量的一個線性組合,與信號源是否相干并沒關系。分析得出,當信號源相干時,其數據的協方差矩陣秩是1,其特征值分解后,只有一個最大特征值,其對應的特征矢量包含所有相干源的信息,因此利用最大特征矢量來解相干。VSV-MUSIC算法需要找出一個矢量,并且這個矢量要含有所有信號源的信息,同樣只適用于均勻線陣。
2.5 矩陣分解MD-MUSIC算法
矩陣分解算法的思想和空間平滑相似,只是矩陣分解類算法陣列接收數據的協方差矩陣,對其進行分塊分解,然后增廣重構。可以證明:理想情況下重構后的矩陣的秩等于信源數。MD算法是針對理想情況下的矩陣重構,與空間平滑技術相似,都是通過降低自由度獲得的,同樣只適用于均勻線陣。
2.6 相干算法仿真及對比
實驗一:兩相干源下MSS-MUSIC算法與傳統MUSIC算法仿真測向對比。
利用Matlab軟件仿真,陣列接收信號為-40°和10°的兩個相干信源,仿真條件見表1所示,并進一步給出了MSS-MUSIC算法和傳統MUSIC算法的測向結果,如圖3所示。
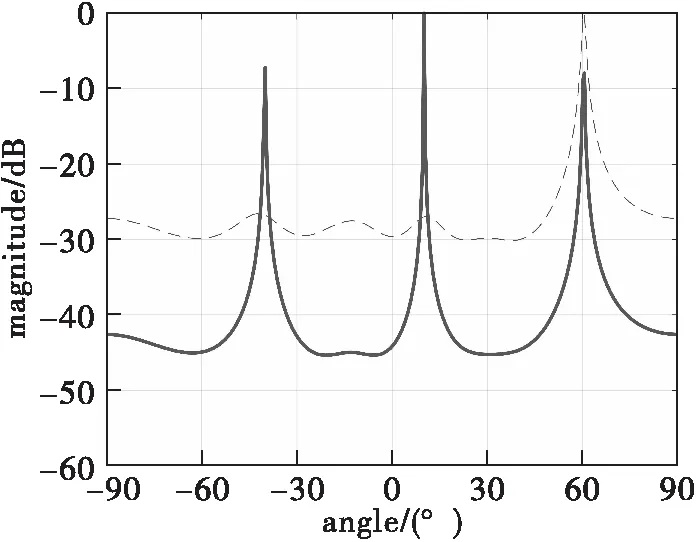
圖3 MSS-MUSIC與MUSIC算法仿真(兩相干信源)
圖3中,虛線表示傳統MUSIC仿真結果,實線表示MSS-MUSIC仿真結果,對比可知,當接收信號為相干信源時,傳統MUSIC算法不能實現DOA測向,而MSS-MUSIC算法可以實現較好的DOA測向。
實驗二:三相干源下MSS-MUSIC算法和ISS-MUSIC的仿真測向對比。
在表1的條件下,-40°、10°以及60°信源采用相干信源,按用Matlab仿真給出了平滑MSS-MUSIC測向結果和ISS-MUSIC測向結果,如圖4所示。
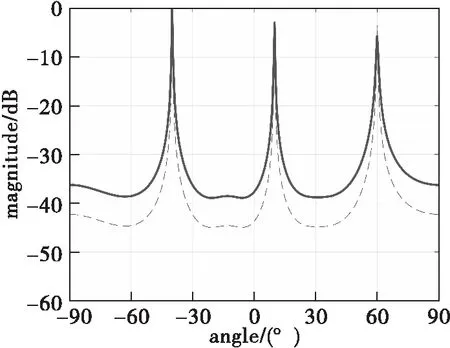
圖4 兩種平滑MUSIC算法仿真(相干信源)
根據圖4對比分析可知,ISS-MUSIC算法形成的譜峰高度要高于MSS-MUSIC算法的譜峰,并且ISS-MUSIC算法的譜峰要比MSS-MUSIC算法的譜峰更尖銳,因此可以認為ISS-MUSIC算法的性能要比MSS-MUSIC優越。
實驗三:三相干源下各類相干算法的仿真測向對比。
在表1的條件下,-40°、10°以及60°信源采用相干信源,用Matlab仿真給出了ISS-MUSIC測向結果、Toeplitz算法測向結果、VSV-MUSIC測向結果以及MD_MUSIC測向結果,如圖5所示。
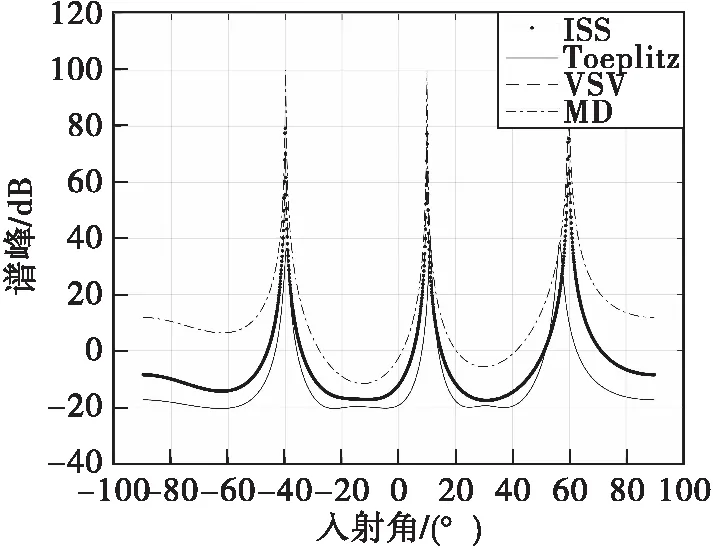
圖5 四種平滑MUSIC算法仿真(相干信源)
圖5可以看出,在三個相干源時,Toeplitz算法測向精度明顯小于其他三種算法,且譜峰的峰值高度也明顯低于其他三種算法,因此Toeplitz算法在三個相干源時,效果最差。在ISS-MUSIC、MD-MUSIC以及VSV-MUSIC測向算法中,MD-MUSIC譜峰值略高于ISS-MUSIC和VSV-MUSIC,圖5可知ISS-MUSIC和VSV-MUSIC曲線幾乎重合,測向精度三種算法大體相當,因此進一步分析在不同信噪比情況下的性能。
實驗四:三相干源下各類相干算法的RMSE對比。
在表1的條件下,信噪比為-10dB到10dB。Matlab仿真給出了ISS-MUSIC測向結果、Toeplitz算法測向結果、VSV-MUSIC測向結果以及MD_MUSIC測向結果,如圖5所示。
圖6可以看出,在不同信噪比的情況下,Toeplitz算法的測向精度最高,且有相對較高的譜峰高度,其次是VSV-MUSIC和MD-MUSIC算法,其他的誤差較大。因此在低信噪比下,Toeplitz算法最優。

圖6 四種滑MUSIC算法仿真(低信噪比)
3 結束語
根據以上分析,對八元超分辨給出以下建議:
1)若實際情況中,要估計三個相關源,且信噪比較高,優先選擇VSV-MUSIC算法,其次是ISS-MUSIC算法以及MD-MUSIC算法。
2)若實際情況中,信噪比較低,且對分辨力和估計誤差要求不高,應該選擇Toeplitz算法。

