基于TanDEM-X數據和改進三階段算法反演森林冠層高度*

張國飛 章皖秋 岳彩榮

(西南林業大學林學院 昆明 650224)

森林是地球上面積最大的陸地生態系統，是全球生物圈中重要的一環，對維系整個地球的生態平衡發揮著不可替代的作用(Minh， 2020)。森林高度是森林最基本的結構參數之一，是重要的林分測量因子，對估算森林生物量、預測生物多樣性等均具有重要意義(Sextonetal., 2009)； 然而，受森林分布、復雜地形條件、天氣條件等因素制約，大范圍開展森林高度測量一直是森林調查的技術難題。合成孔徑雷達(synthetic aperture radar，SAR)是20世紀50年代末研制成功的一種微波傳感器，具有獲取植被表面極化和干涉模式數據的能力，被廣泛用于森林結構和生物物理參數反演(Kumaretal., 2017)，其中合成孔徑雷達干涉測量(interferometric synthetic aperture radar， InSAR)和極化合成孔徑雷達干涉測量(polarimetric and interferometric synthetic aperture radar， PolInSAR)對森林體散射的形狀、方向和垂直結構比較敏感，可獲得不同植被高度下不同極化干涉復相干，大量用于森林結構監測(Cloudeetal., 1998； Papathanassiouetal., 2001)。

PolInSAR技術綜合InSAR技術對體散射垂直結構的量度性以及PolSAR技術對體散射形狀和方位的敏感性，能夠生成任意極化散射機制下的復相干影像，各極化散射機制與森林結構特征相對應，為提取森林結構信息奠定了物理基礎(Cloudeetal., 1998； Bamleretal., 1998； Papathanassiouetal., 2001)。Cloude等(1998)首次利用不同散射機制干涉優化算法估測了森林冠層高度。Treuhaft等(1996； 1999； 2000)提出的RVoG(random-volume-over-ground)模型是當前PolInSAR技術估測森林冠層高度機理模型的基礎。Papathanassiou(2001)將極化干涉相干優化算法與RVoG模型相結合，提出了單基線RVoG復相干模型樹高反演6參數法，并采用非線性迭代優化進行解算。Cloude(2003)基于復相干幾何分布特征提出的RVoG復相干模型經典三階段算法，簡化了森林冠層高度估測的復雜性(Garestieretal., 2007； 2008； Chenetal., 2011； Luetal., 2013)。但由于受地形相位估計誤差、純體相干性估計誤差的影響，經典三階段算法反演森林冠層高度存在低估現象(Kumaretal., 2017； Kugleretal., 2015； Khatietal., 2015； Denbinaetal., 2016； 解清華等， 2015； 章皖秋， 2018)，如Khati等(2015)采用經典三階段算法和TanDEM-X數據反演印度熱帶林區森林冠層高度，低估了7～10 m； 解清華等(2015)通過SAR數據仿真發現，在郁閉度較大的森林中各極化通道相位中心相對集中，地面相位中心偏高，森林冠層高度也被低估(RVoG模型通過求解地面相位中心與體散射相位中心之間的距離及體散射幅度估測森林冠層高度)。

RVoG模型經典三階段算法根據L、P長波長的極化散射特征解算地面相位和體散射，在應用于短波長X 波段時會出現地面相位、純體散射復相干估計不準確等問題，導致無法估測出合理的森林冠層高度。當前在軌星載SAR系統數據大多需要重軌獲取，森林冠層高度估測時受時間失相干影響嚴重(Kumaretal., 2017； 范亞雄等， 2020)，而TanDEM-X星載數據采用一發雙收模式對地物進行觀測，零時間基線。鑒于此，本研究從X波段的極化散射機制出發，提出針對X波段數據RVoG模型經典三階段反演算法的優化方法，并用TanDEM-X數據進行驗證，以解決RVoG模型實際應用中模型成立條件難以嚴格滿足、受地形影響導致森林冠層高度估測精度不高的問題。

1 研究區概況與數據

1.1 研究區概況

研究區位于云南省普洱市思茅區(22.8°N, 100.9°E)，地處北回歸線附近，滇南熱帶與南亞熱帶的過渡地帶，干濕季分明，年均氣溫15～20.3 ℃，年降雨量1 100～2 780 mm，平均海拔1 320 m。區內森林覆蓋率67%，思茅松(Pinuskesiyavar.langbianensis)為主要森林類型，林內常混交紅木荷(Schimawallichii)、刺栲(Castanopsishystrix)、小果錐(C.fleuryi)、茶梨(Annesleafragrans)和毛銀柴(Aporusavillosa)等喬木樹種(李江， 2011； 章皖秋， 2018)。

1.2 樣地數據

選取思茅松人工林為研究對象，設置90塊調查樣地(圖1)，其中思茅松純林樣地47塊、混交林(以思茅松為主要優勢樹種的針闊混交林)樣地43塊。數據采集時間為2018年12月和2020年1月，采用分層隨機抽樣設置樣地，大小為20 m×20 m，在樣地范圍內進行每木調查，起測胸徑5 cm，調查因子包括樹種、樹高、胸徑、郁閉度和地況，見表1。

圖1 研究區位置(上)與樣地分布(下)Fig. 1 Location of study area (top) and plot distribution (bottom)

表1 調查樣地數量和林分參數Tab.1 Number and stand parameters of field plots

森林高度估測基于對森林冠層微波散射中心位置的推斷，估測值理論上與森林冠層表面高度最接近，但考慮到地面測量難度，本研究以樣地內單木樹高算術平均值作為森林冠層高度的替代值。研究區森林高度主要分布在10～20 m，平均高度15.7 m(純林平均高度14.2 m，混交林平均高度17.3 m)，最小高度3.6 m，最大高度24.0 m。

1.3 衛星數據

采用零時間基線的TerraSAR-X和TanDEM-X全極化干涉產品，產品參數描述見表2。

圖2所示為TDX CoSSC產品主輔圖像Pauli假彩色合成圖(HH-VV、HV+VH、HH+VV)。2種數據集分布于HH、HV、VH和VV 4個極化通道。在研究區范圍內，地表產生的面散射、樹枝和樹葉隨機定向產生的體散射、地表-樹干相互作用產生的二面角散射3種散射成分容易出現。

表2 SAR 數據描述Tab.2 Description of SAR data

圖2 主(左)輔(右)圖像Pauli假彩色合成Fig. 2 Pauli colour composite of master (left) and slave (right) images紅: HH-VV； 綠: HV+VH； 藍: HH+VV。Red: HH-VV; Green: HV+VH; Blue: HH+VV.

2 研究方法

2.1 RVoG模型

Treuhaft等(1996； 1999； 2000)提出一種帶有地面回波的隨機方位體積層模型(RVoG)森林高度反演方法，森林被視為覆蓋在地表的隨機體粒子層，包含大量隨機分布且相互獨立的體散粒微粒。

在雷達波入射角為θ的二層RVoG模型(圖3)中，地表被認為是雷達波無法穿透的表面散射層，高度為Z0，引起地面相位為φg，植被厚度為hv，森林冠層高度為Z0+hv。假定植被層的散射能量隨高度增加呈指數變化，消除配準誤差、大氣去相干等影響后，基于RVoG模型的極化干涉復相干γ(ω)表示(Treuhaftetal., 1999； Luetal., 2013； Kugleretal., 2015)如下：

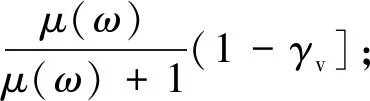
(1)

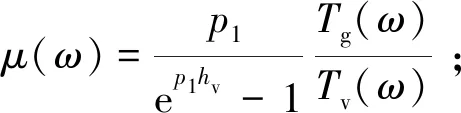
(2)

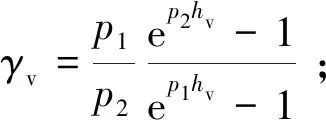
(3)

(4)

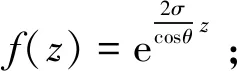
圖3 RVoG 模型Fig. 3 RVoG model

在RVoG復相干模型中，θ、λ、Δθ、kz可通過SAR平臺系統參數代入獲得；φg、μ(ω)、hv、σ可通過求解RVoG復相干模型來估測森林冠層高度(李廷偉等， 2009； 章皖秋， 2018)。

2.2 不同優化改進的三階段算法反演森林冠層高度

本研究設計4種方法反演森林冠層高度，主要步驟見圖4。方法1采用經典三階段反演算法，作為基準模型； 其他3種方法分別為地面相位優化估計、純體散射復相干優化估計和低估補償改進三階段反演算法，是一個逐步改進的優化過程，以檢驗優化方法在森林高度估測方面的性能增益。地面相位優化估計、純體散射復相干優化估計處于三階段反演算法的第二、三階段，低估補償改進算法針對三階段反演算法估測的地面相位可能高于實際地表導致的高度低估情形，3種優化方法亦可單獨使用。圖4中陰影步驟為方法改進部分。

2.2.1 方法1——經典三階段反演算法 經典三階段算法是一種基于RVoG模型的幾何分布特征反演算法，分為3個階段(陳兵等， 2008)。

第一階段： 各極化復相干直線擬合。根據式(1)，各極化復相干(包括HH、HV、VH、VV、HH+VV、HH-VV、LL、RR、OPT1、OPT2、OPT3、PDhigh、PDlow等13種)在復平面單位圓(complex unit circle，CUC)的軌跡呈直線形式。三階段算法采用總體最小二乘法擬合復相干擬合直線的參數(Minhetal., 2014； Cloude， 2015)，復相干擬合直線(complex fitting line，CFL)與CUC的2個交點的相位作為候選地面相位，見圖5。

第二階段： 從候選交點中確定地面相位。有效地體散射幅度比μ(ω)可以克服這一模糊性，即當μ(ω)→∞，γ(ω)僅包括林下地表的面散射。經典三階段算法選擇擬合直線上距離γHV較遠的交點作為林下地表的面散射，其相位為地面相位(Cloud， 2003； Kugleretal., 2015)。

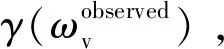
圖4 4種方法的主要步驟Fig. 4 Main procedures for the four different methods

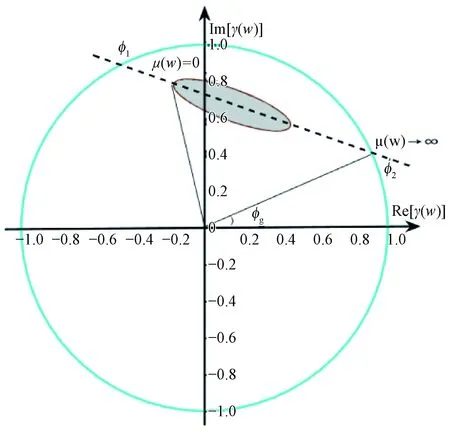
圖5 復平面單位圓內相干線的幾何表示Fig. 5 The geometrical representation of coherence line inside the complex unit circle

為了檢驗各優化方法在森林高度估測方面的性能增益，本研究4種方法均采用固定的消光系數(σ)。已有研究發現，熱帶闊葉林和針葉林的消光系數為0.1～0.9 dB·m-1(Hajnseketal., 2009； Caicoyaetal., 2012)，反演森林高度時，針葉林的消光系數固定值為0.2 dB·m-1(Caicoyaetal., 2012)、熱帶森林的消光系數固定值為0.3 dB·m-1(Hajnseketal., 2009)和0.4 dB·m-1(廖展芒， 2019)。本研究中，思茅松林消光系數取0.2 dB·m-1； 另外，hv限制在5～30 m之間。

在方法1中，估測的森林冠層高度稱為Classic_H。

2.2.2 方法2——地面相位優化的三階段反演算法 該方法旨在檢驗地面相位優化的三階段反演算法對森林冠層高度估測的影響，算法其余部分與方法1相同。

經典三階段算法中，地面相位通過比較γHV與候選交點的距離進行估測(Papathanassiouetal., 2001； Kriegeretal., 2007； 解清華等， 2015)，但受地形起伏和枝葉生長方向不確定性的影響，X波段HV極化通道不一定在林冠頂部，有可能接近地面(Cloude， 2015； Denbinaetal., 2016)，同時X波段極化復相干分布相對集中，并趨于某一交點(Kriegeretal., 2007； Kugleretal., 2015)，在這2種情況下，經典三階段算法可能錯誤估測地面相位。本研究參考γPDlow估測地面相位，γPDlow和γPDhigh是極化空間相位差異最大的極化干涉復相干，γPDlow相位中心接近森林底部(Flynnetal., 2002； Kriegeretal., 2007； 解清華等， 2015)，同側的交點應該是地面層交點。

具體步驟如下：

第一步，計算各觀測復相干值與2個交點之間的相位差，并分別按從小到大排序：

Δφi,ω=abs{arg[(γ(ω)e-jφi]}，i=1,2；

(5)

(6)

第二步，若γPDlow在Rank 1中位居前3位，則φg=φ1； 若γPDlow在Rank 2中位居前3位，則φg=φ2； 若2組排序均沒有超過前3位，則φ1和φ2分別作為候選地面相位，得到2個冠層高度估測值，選擇估測值在合理范圍內的候選地面相位作為φg輸出(Cloude， 2003； 章皖秋， 2018)。

在方法2中，估測的森林冠層高度稱為Improve_H1。

2.2.3 方法3——純體散射復相干優化的三階段反演算法 該方法旨在檢驗純體散射復相干優化的三階段反演算法對森林冠層高度估測的影響，算法其余部分與方法2相同。

經典三階段算法中，γHV作為純體散射復相干觀測值，其在擬合直線上的垂直投影作為純體散射復相干估計值，此時，μHV接近0，γHV與地面γ(wg)距離最遠(Papathanassiouetal.， 2001； 章皖秋， 2018)，但垂直投影會改變純體散射復相干有效觀測值的模值和相位，容易引入誤差(Cloude， 2015； 章皖秋， 2018)，見圖6。因此，本研究提出純體散射優化估計，即從各極化復相干中篩選出純體散射復相干觀測值，并采用模值不變投影方法估計純體散射。

圖6 模值不變方式投影Fig. 6 The projection of unchanged module of complex coherence

具體步驟如下：

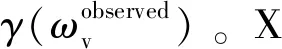
第二步，采用模值不變投影方法估計純體散射γ(ωv)。首先，以坐標原點為圓心、以體散射有效觀測值γ(ωobserved)的模值為半徑作圓； 然后，計算圓與擬合直線(CFL)的交點p1和p2，取離垂直投影點p′距離較小的交點p1作為純體散射γ(ωv)，如下式：

(7)

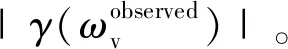
若體散射觀測值γ(ωobserved)距擬合直線距離很近，則p1與p′相差不是很大； 若圓與擬合直線沒有交點，則用垂直投影點p′替代，如圖6所示。

在方法3中，估測的森林冠層高度稱為Improved_H2。

2.2.4 方法4——低估補償改進的三階段反演算法 該方法旨在檢驗低估補償改進的三階段反演算法對森林冠層高度估測的影響，算法其余部分與方法3相同。

X波段波長短，在森林區域易出現穿透不深的情況，尤其在局部入射角較大的背向雷達波波面上或林冠茂密的區域，經典三階段算法估測的地面相位可能高于實際地表，造成森林冠層高度低估(Parksetal., 2013； 解清華等， 2015)。因此，本研究基于γPDlow相位更接近地表的假設條件，提出一種三階段低估補償算法，以改善X波段SAR數據估測時森林冠層高度被低估的現象。

具體步驟如下：

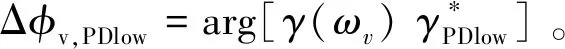
第二步，判斷地面相位位置。如果 Δφv,g≥Δφv,PDlow，地面相位處于γPDlow復相干相位下方，森林冠層估測高度不需要補償； 如果Δφv,g<Δφv,PDlow，地面相位估計值高于γPDlow相位，森林冠層估測高度需要補償，進入下一步。

第三步，高度補償。計算地面相位與γPDlow的相位差，并轉換為高度差，將高度差加Improved_H2上，如下式：

(8)

圖7 研究區的地面相位Fig. 7 Estimated ground phase of study areaa. 參考γHV的地面相位Ground phase estimated referring to γHV； b. 參考γPDlow的地面相位Ground phase estimated referring to γPDlow.

在方法4中，估測的森林冠層高度稱為Compensated_H。

采用皮爾遜相關系數(r)、均方根誤差(RMSE)和偏離率(bias)對所有算法進行檢驗：

(9)

(10)

(11)

3 結果與分析

3.1 地面相位優化

根據RVoG模型，地面相位是由林下地表高程引起的相位。林下地表高程屬于連續表面，地面相位形成的條紋應清晰光滑、有規律性。與經典三階段算法估測的地面相位(圖7a)相比，優化三階段算法估測的地面相位(圖7b)條紋清晰、斑點少，表明以γPDlow相位為參考的地面相位優化估計有利于改善森林冠層高度估測。

3.2 森林冠層高度估測

經典三階段反演算法和TanDEM-X SAR數據反演森林冠層高度出現低估現象，90塊思茅松樣地偏離率為-26.20 m，Classic_H與樣地實測高度的相關性低，精度不高(r=0.11，RMSE=7.16 m)。圖8a1、b1顯示，大部分散點分布在y=x線以下。

與Classic_H相比，地面相位優化可改善森林冠層高度低估現象，偏離率從-26.20 m提高至-9.19 m，Improved_H1與樣地實測高度的相關性和精度均有所提高(r=0.46，RMSE=4.00 m)。圖8a2、b2顯示，大部分散點分布在y=x線兩側，說明地面相位優化方法有效。

與Improved_H1相比，純體散射復相干優化的三階段反演算法在森林冠層高度低估和模型反演精度方面改善效果不明顯(bias從-9.19 m提高至-7.31 m，RMSE從4.00 m提高至3.57 m)； 但篩選體散射復相干觀測值和模值不變投影方法使估測高度與實測高度的相關性優化(r從0.46提高至0.62)，說明個別樣地的估測精度有所提高(圖8a3、b3)。

與Improved_H2相比，低估補償改進的三階段反演算法可進一步改善森林冠層高度低估現象，偏離率從-7.31 m提高至-1.69 m，Compensated_H與樣地實測高度的相關性和精度有所提高(r=0.79，RMSE=2.56 m)(圖8a4、b4)。

從4次試驗的反演結果看，與思茅松混交林相比，三階段優化算法對思茅松純林的適應性更好。在方法1、2、3中，增加思茅松混交林樣地后，總體樣本森林冠層高度與實測高度的皮爾遜相關系數降低，均方根誤差精度降低； 在方法4中，增加思茅松混交林樣地后，總體樣本森林冠層高度與實測高度的皮爾遜相關系數沒有太大變化，而均方根誤差精度降低(表3)。

圖8 估測高度和樣地實測高度的散點圖Fig. 8 The scatter plots between estimation heights and measured heightsa1、a2、a3和a4為思茅松混交林樣地； b1、b2、b3和b4為思茅松純林樣地； 橙色圈內的樣地為思茅松幼齡林。a1,a2,a3 and a4： plots in P. kesiya var. langbianensis mixed forests； b1,b2,b3 and b4： plots in P. kesiya var. langbianensis pure forest； the plots in orange circle is young P. kesiya var. langbianensis forest.

總體結果表明，在4種森林冠層高度估測方法中，本研究提出的優化方法能夠逐步提高估測精度。圖9為森林冠層估測高度Compensated_H分布。從反演結果來看，研究區森林冠層高度主要分布在16～22 m之間(圖9b)，與研究區2016年森林二調數據樣地林分平均高度(16～20 m)具有一致性(云南省林業調查規劃院， 2016)。

4 討論

方法1經典三階段反演算法估測森林冠層高度存在低估現象，可能是X波段穿透性差引起地面相位和純體散射復相干估計不準確導致的(解清華等， 2015； Denbinaetal., 2016； 章皖秋， 2018； Parksetal., 2013)。針對地面相位估計不準確的問題，本研究提出參考γPDlow估計地面相位，結果發現優化后的地面相位比經典三階段算法條紋更清晰。針對純體散射復相干估計不準確的問題，本研究提出純體散射復相干優化估計，從各極化復相干中篩選出純體散射觀測值，采用模值不變投影方法估計純體散射。方法2和3均可改善三階段反演算法的森林冠層高度估測精度。

森林結構是森林冠層高度估測精度的主要影響因素之一。在幼齡林或稀疏林分中，郁閉度較小，雷達波大部分穿透地面，森林冠層體散射在回波信號中占比較小，純體散射復相干的一部分是由地面復相干引起的，導致森林冠層高度異常估計(解清華等， 2015； Denbinaetal., 2016； 章皖秋， 2018； Parksetal., 2013； Sadeghietal., 2016)，如研究區2塊幼齡林樣地(林分平均高度為4 m和3.6 m)的高度估測出現異常(圖8b中已標注)。在冠層密度中等、垂直結構單一的針葉純林林分中，冠層結構相似，外形近似隨機散射粒子層，回波信號主要來自整個冠層，采用優化三階段反演算法和TanDEM-X SAR數據估測的森林冠層高度接近實測高度。在垂直結構復雜林分中，如針闊混交林，呈現2層或多層樹冠結構，郁密度較大，雷達散射回波信號由多林層回波的相干疊加，散射相中心位置隨林層結構不同而變化，森林冠層高度估測值與實測值的關系復雜多變。因此，當稀疏林分中郁閉度較小或垂直結構復雜林分中郁密度較大時，三階段算法反演森林冠層高度可能會出現異常，估測精度不高(章皖秋， 2018)。從本研究反演結果看，與思茅松混交林相比，三階段優化算法對思茅松純林的適應性更好。在方法4中，思茅松純林冠層估測高度與實測高度的反演精度(r=0.81，RMSE=2.27 m)優于思茅松混交林(r=0.72，RMSE=2.87 m)。后續研究中，針對稀疏林地或裸地，可通過對地物的準確分類，剔除非林地區域和近“裸”林分，提高估測精度； 針對垂直結構復雜林分，可利用多頻多時相SAR數據聯合探索復雜冠層結構與微波散射機制的關系； 針對估測值異常現象，可研究不同地面單元的自適應估測方法，如通過空間濾波和重采樣等降低空間分辨率技術，用區域平均值、中值等統計值代替異常估測的地面分辨率單元，減小局部估測偏差，為大面積中、低比例尺度的森林冠層高度提供基礎數據。

表3 4種三階段反演算法的驗證結果Tab.3 Validation results of the three-stage inversion algorithm from all approaches

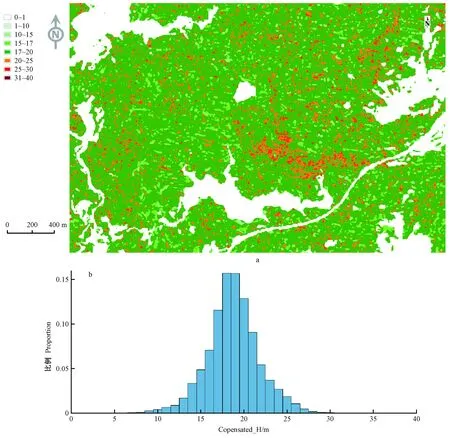
圖9 研究區域(部分)估測森林冠層高度分布(a)和直方圖(b)Fig. 9 Predicted maps(parts) of Compensated_H in the study area

Khati等(2015)采用經典三階段反演算法和TanDEM-X數據反演印度熱帶林區森林冠層高度，17塊樣地森林冠層估測高度出現低估現象(-7～-10 m)，RMSE為7.60 m，與本研究中方法1結果相當。馮琦等(2016)利用機載X波段HH干涉數據和SINC模型估測地形平緩的內蒙古白樺(Betulaplatyphylla)林冠層高度，估測高度與LiDAR測量高度的相關系數為0.86，RMSE為2.74 m，高于本研究方法4估測結果，原因可能源于本文研究區地形起伏較大。Kugler等(2015)提出一種地形校正的三階段反演算法，用2種不同入射角的TanDEM-X SAR數據解決透視收縮問題，用外部DEM優化地面相位估計和降低坡度對估測高度的影響，估測高度和LiDAR測量高度的相關系數為0.94，RMSE為1.32 m； 但地形校正的三階段反演算法需要數據較多，不利于實際應用。Kumar等(2017)采用TanDEM-X數據和三階段反演算法估測印度北方坎德邦的Barkot和Thano森林，估測高度與實測高度的相關系數為0.74，RMSE為3.19 m，相比本研究方法4估測結果稍差。

綜上所述，優化三階段反演算法估測森林冠層高度僅以單基線全極化SAR數據為數據源，在大多數地區均可以獲得較高估測精度。

5 結論

采用經典三階段反演算法和TanDEM-X SAR數據估測森林冠層高度時，由于X波段波長短，穿透力差，存在地面相位和純體散射復相干估計不準確的問題，導致無法估測出合理的森林冠層高度。本研究從X波段的極化散射機制出發，對RVoG模型經典三階段反演算法進行優化和改進，提出適合X波段SAR數據的優化三階段反演算法，包括地面相位、純體散射復相干優化和低估補償算法，以普洱市思茅松林為研究對象，獲得較好估測精度，冠層估測高度和實測高度的相關系數在0.72～0.81之間，均方根誤差在2.00～3.00 m范圍內。優化三階段算法反演精度較經典三階段算法有了較大提高，利用該方法和TanDEM-X SAR數據可實現大范圍森林高度的估測。