基于局部線性模型的傳感器故障檢測仿真

周 洋，羅 棋，孫伶俐 羅俊秋

(1. 中國地震局地震研究所，湖北 武漢 430071；2. 湖北省地震局，湖北 武漢 430071)

1 引言

湖北區域地球物理臺網目前共計23個臺站83套儀器，其中地下流體儀器41套，SWY-II型數字式水位儀9套、SZW-1A及SZW-II數字式溫度計15套、RTP-II型氣溫氣壓雨量綜合觀測儀3套、WYY-1型氣象三要素觀測儀14套[1]。地下流體儀器種類繁多、在網運行數量也是在各觀測手段(重力、形變、電磁、流體)中居首，同樣發生故障的概率與頻次也是最多。故尋求一種應用前景更為廣闊的傳感器故障檢測方法顯得尤為重要。

國內外在傳感器故障方面的研究成果很多，方法也是多種多樣，硬件冗余方法，解析冗余方法，神經網絡方法，信號處理方法等等都得到了很好的研究和應用[2]。文獻[3-7]提出了基于小波變換的傳感器故障診斷方法。文獻[8]主要介紹了連續小波變換和BP神經網絡在傳感器故障診斷中的應用。文獻[9-10]采用冗余傳感器進行故障檢測。文獻[11]提出了基于小波包的MSPCA模型，并應用于傳感器的故障診斷。文獻[12]基于輸入輸出信號趨勢分析，提出基于形態學-小波的傳感器故障檢測與診斷的新算法。文獻[13]主要利用三層前饋神經網絡，用反向傳播算法進行訓練，從而對一個一階線性系統和一個二階非線性振蕩系統中的傳感器進行了故障診斷，并且取得了較好的效果。文獻[14-15]應用了多模型自適應估計方法。

本文提出了一種新的傳感器故障FDI方法，并將其應用于一個非線性動態現實過程。過程的局部線性模型的參數用于生成類似于奇偶空間方法的結構殘差。這使得在廣泛變化的工作條件下，僅使用一個非線性模型，就可以連續地對非線性過程的傳感器故障進行直接故障診斷。以地震地下流體儀器傳感器故障檢測為例說明了該方法的適用性。

2 模糊過程模型

局部線性模型樹(LOLIMOT)算法是基于一個非線性動態函數的思想，其中u1到um為m個物理輸入，y為輸出。

y(k)=y(x(k))，x(k)=[x1(k)，x2(k)，…，xn(k)]T

x(k)=[u1(k-1)…u1(k-nu，1)，…

um(k-1)…um(k-nu，m)，

y(k-1)…y(k-ny)]

(1)

通過分段線性模型，它們物理輸入的時延值和過程輸出的時延值構成了維數為n的模型輸入空間，每個局部模型只在輸入空間的某個子區域上有效。局部模型有效的分區不是清晰的而是模糊的。因此，輸入空間中某一點的一個局部模型i的有效性由加權函數zi表示，該加權函數在整個輸入空間上連續定義，并從零(無效)縮放到一(完全有效)。該方法采用歸一化高斯加權函數Φi。每一個局部模型輸出yi被計算為輸入xi(超平面)的線性函數。整個模型的輸出被計算為所有M個局部線性模型輸出的加權和。

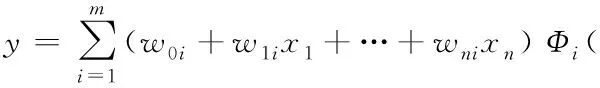
(2)

其中，w0i…wni是第i個線性回歸模型的參數，x1…xn是輸入、而Φi是以ci為中心，σi為標準偏差的歸一化高斯加權第i個模型的函數。模型輸出的這種計算推導出本地模型輸出之間的非線性插值。 高斯描述為

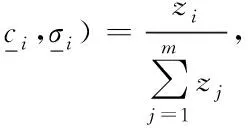
(3)

這種類型的模型被稱為通過重疊局部基函數對線性模型進行插值的局部模型網絡。 事實證明，該模型和式(3)中的版本是通用的，因此顯然具有相同的空閑參數數量的屬性。 該模型也可以解釋為具有高斯隸屬函數的Tagaki-Sugeno模糊模型。由于所有局部線性函數都依賴于相同的輸入xi，式(2)可以寫成下面形式

=w0+w1x1+…+wnxn

(4)

這類似于參數wi取決于輸入xi的線性過程描述。 圖1闡明了局部模型方法。局部模型的參數以及高斯模型的中心和標準偏差是在兩個構造循環中確定的。在下文中，參數wi可用于生成結構化殘差以隔離傳感器故障。

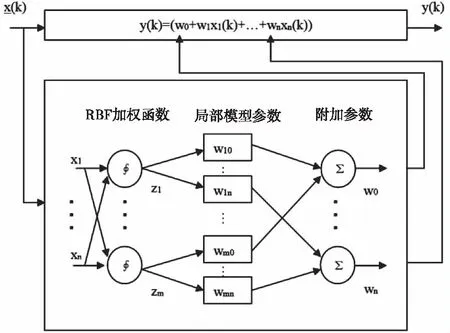
圖1 局部模型方法

3 故障檢測方案

為了檢測和隔離傳感器故障，大多數FDI模型的殘差r(k)具有以下屬性：

r(k)≈0 無故障情況(噪聲影響，不確定性)

r(k)≠0 發生故障

其中k表示某個采樣間隔。 殘差可以是以至少一個測量量對特定殘差沒有影響的方式進行設計。如果測量有誤，則解耦殘差很小，而其它所有受影響。偏斜和未偏斜殘差的模式指示故障的位置。產生這些所謂的結構化殘差的一種方法是基于狀態空間線性過程描述的奇偶校驗空間方法。在下一個小節中，直接從線性生成結構化殘差的方法介紹微分方程。取決于實際輸入參數wi的偽線性方程(5)用于生成殘差。

3.1 結構化殘差的生成

假設具有m個輸入ui和r個輸出yi的非線性離散系統可以進行局部線性模型建模

… = …

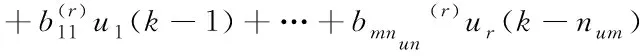
(5)

根據式(5)，參數aij和bij不是恒定的，而是取決于模型輸入xi。引入長度為tw≥n的時間窗口，其中n=max(nym，num)。使用先前的測量參數tw可推導出以向量形式表示的tw-n時延方程。

A1y1(k：k-tw)+…+Aryr(k：k-tw)=

B1u1(k-1：k-tw)+…+Bmum(k-1：k-tw)

(6)

其中dim(yi)=[1*r■(tw+1)]， dim(ui)=[1*r■tw]， dim(Ai)=[tw*r■(tw+1)]， dim(Bi)=[tw*r■tw].Y和U包含時間窗口內的所有先前輸出和輸入。

yi(k：k-tw)=[yi(k)，yi(k-1)，…，yi(k-tw)]T

ui(k-1：k-tw)=[ui(k-1)，…，ui(k-tw)]T

(7)

Ai和Bi包含輸出和輸入的所有參數。注意由于(8)和(9)的結構，輸入ui或輸出yi的所有實際值和延遲值僅分別用矩陣Bi或Ai加權。使用(7)并引入殘差生成器矩陣W，在無故障情況下接近零的殘差可以通過以下方式設計。

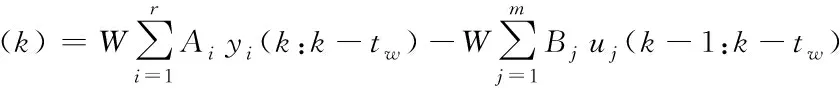
(8)

從(8)和(9)可以看出，選擇W的wT行向量來滿足條件

WTBi=0，或者wTAi=0

(9)

分別導致殘差與輸入ui或輸出yi解耦。W的設計方式是，每個行向量都是不同的Ai或Bi矩陣的零空間。這導致結構化殘差矢量r(k)具有很強隔離形式。時間窗tw的長度應選擇為可能的非平凡解決方案(wT≠0)。存在一個n*m的矩陣X∈[AiBi]，如果滿足

rank(Xi)>m

(10)

為了簡單起見，將省略離散時間k。

3.2 一般FDI方案

偽線性模型(5)的參數用于為每個樣本間隔生成結構化殘差，從而實現上述設計過程。 使用實際和先前的過程測量來評估殘差。 為了檢測殘余變形，使用固定的閾值。

如前所述，實際過程參數wi不是恒定的，而是取決于輸入和輸出。在無故障的情況下，這對殘差沒有影響，但是如果在模型輸入xi上發生故障，則加權函數(3)會受到影響。因此，從局部模糊模型得出的參數wi與式(5)在無故障情況下的參數是不同的。 這影響了去耦殘差。 為了避免錯誤警報并實現正確的故障隔離，有必要選擇閾值，以使解耦后的殘差保持在閾值以下。

3.3 殘差的靈敏度

假設用(7)描述系統，并使用(9)生成殘差。假設在輸出傳感器yj上發生故障fyj(可以用相同的方式處理u上的故障)并影響矩陣元素Ai和Bi。然后，殘余矢量將通過以下方式受到影響。

rfyj=Wfyj(Aj+△Aj)(yj+△yj)+

(11)

由于yj的變化，所有取決于yj的殘差都會偏轉，并且參數為矩陣。為了將殘差j與yj解耦，設計W的第j行向量來滿足方程。

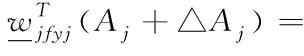
(12)

解耦后的殘差可計算為

rjfyj=rj+△rj=(wj+△wj)T

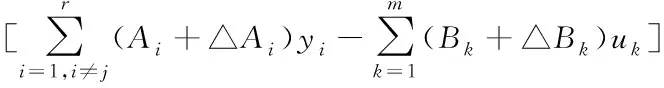
(13)

殘差偏轉△rj可通過(9)和(14)計算得出

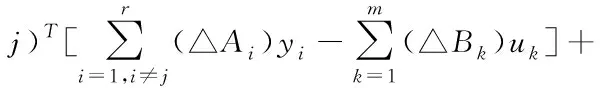
(14)

該方程式描述了去耦殘差，可通過以下方式用于閾值設計：

通過將x設置為恒定值來選擇一個工作點。

通過本地模型(4)的加權疊加來計算(8)的參數。

用最大參數差△搜索局部模型到后者(僅在非線性輸入方向上)。

為這些參數集計算W和B，并計算(14)中△的差異。

對不同的操作點重復此過程。

該程序可評估殘差偏轉，并可用于殘差rj的閾值trj的設計。

trj=△rj+Crj

(15)

其中C是由于噪聲和模型不確定性而產生的常數偏移項。

3.4 并行和系列并行模型

流程的每個動態模型都可用于反饋輸出預測的并行模式，或將以前的過程輸出作為模型輸入的系列并行模式。

系列并行模式執行一步預測，并且減小輸出傳感器故障的影響。因此，在此過程中，過程模型僅用于檢測輸入故障。并行模型領先多步系列參數模型，并行模型預測會導致殘差如果發生輸出故障，則測量永久偏轉。該模型可用于輸出故障檢測。

4 仿真研究

本文在上述模型算法的基礎上，結合湖北省地震地下流體數據實例進行仿真。在儀器傳感器故障檢測前先對觀測數據做去噪處理，以期保留信號的有效成份，濾除噪聲部分。

4.1 信號去噪

同傳統的數據處理方法相比，小波濾波方法具有獨特的優勢，即能夠在去除噪聲的同時，很好的保留信號的突變部分或圖像的邊緣。而本文提出的一種新的非線性過程的局部線性模型算法則比傳統的小波濾波算法更具優越性。表1給出幾種不同算法的定性比較。

表1 幾種濾波方法的定性比較

以2020年4月荊門臺1測點水溫數據為例，給出數據信號在4種不同的濾波算法處理下的結果，如圖2。

圖2 幾種濾波方法比較

從圖2得到的結果來看，局部線性模型法對噪聲有很好的抑制作用，去噪效果明顯，為實際工程應用中提供了一個新的研究思路。

4.2 傳感器故障檢測仿真

選取湖北省房縣三海村臺、鐘祥馬嶺臺、秭歸臺水溫儀傳感器進行檢測仿真，時間跨度200天。如圖3-5。

圖3 房縣三海村臺傳感器檢測

為更好的檢測傳感器故障，對每組數據先進行濾波去噪，將濾波信號平移以示區分原始信號與故障信號。然后用算法對濾波信號檢測傳感器出現故障的時間節點。房縣三海村臺水溫儀傳感器在第45天左右出現明顯下降臺階，可判斷為故障出現時間段，再依據起止日期，便可準確定位故障出現的時間點。顯然，根據原始信號和濾波信號無法判斷。

同理，鐘祥馬嶺臺在第120天同樣檢測出故障起始點。而秭歸臺在第100天出現故障，且信號噪聲明顯增多。實現仿真時間段可根據實際需要實時調整，系統可移植性、靈活性強。表2為上述幾種算法的檢測性能比較。

圖4 鐘祥馬嶺臺傳感器檢測

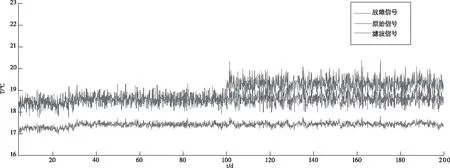
圖5 秭歸臺傳感器檢測

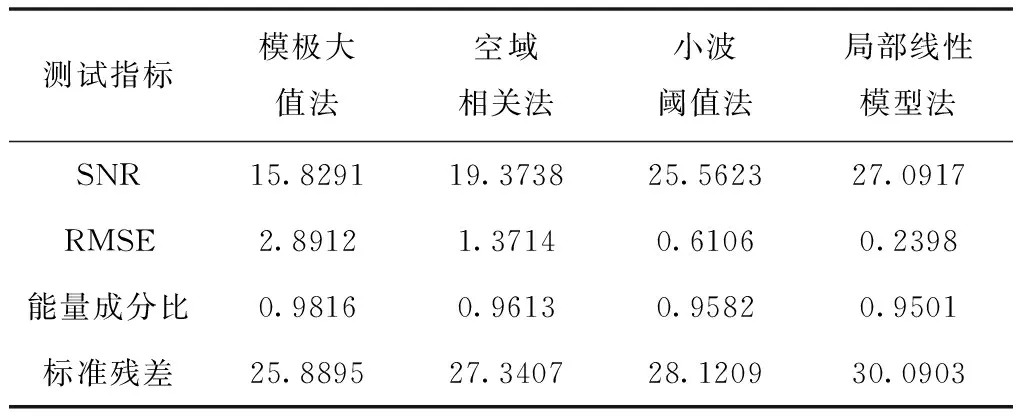
表2 幾種算法檢測的結果比較

從SNR和RMSE的定義可知，SNR值越大，檢測效果越好；RMSE反之[16]。能量成分比越小，檢測效果越好，標準殘差反之。而局部線性模型法很好地保留了信號發展初期的高頻特性，最大限度地反應了原信號本身的性質，且性能參數優于其它幾種算法。

5 結論

本文提出一種非線性過程的局部線性模型傳感器故障檢測的新方法。并利用該模型對湖北省地震地下流體臺站儀器傳感器故障檢測進行仿真，得出以下結論：

1)過程的局部線性模型的參數用于生成結構化殘差。該模型允許評估殘差的靈敏度，該靈敏度可用于閾值設計。 這些方法的結合為檢測和隔離突發故障以及非線性過程中緩慢發展的故障提供了強大的工具。

2)該模型對地下流體儀器傳感器故障檢測準確、快速，信號消噪效果好，為臺站檢測傳感器故障提供一種新的研究方向和方法，為儀器維護人員提供一種新的檢測手段和途徑。

3)該算法不依賴于具體的對象的數學模型，可移植性強。仿真結果可迅速判斷故障發生的時刻。該模型可推廣應用至其它觀測手段的傳感器故障檢測，如形變、重力、電磁等。