數列通項公式的唯一性之規范探究

◎劉子輝

(鹽城幼兒師范高等專科學校，江蘇 鹽城 224000)

課堂教學是師生之間、生生之間交往互動和共同發展的過程課堂教學中，我們經常碰到各種各樣的問題，這些問題往往可以作為教研資源一名教師，特別是青年教師，必須牢固樹立問題意識，善于用審慎的目光觀察各種教學現象，養成收集、整理、分析、鉆研這些教學現象的習慣，不斷提高自己發現問題、提出問題、分析問題、解決問題的能力，從而提升自己的專業知識水平下面，筆者以數列教學為例，針對教材、教輔和學生作業中經常出現的一些似是而非的表述，闡述一下筆者分析、思考的過程，以求教于讀者

一、發現問題

(一)背景材料

在一些教材、教輔及學生的作業中，我們經常可以看到下面的表述：

寫出數列的一個通項公式，使它的前4項分別是2，4，6，8

此數列的前4項2，4，6，8都是項數的2倍，所以它的通項公式是=2

一些練習冊和校內考試的試卷中，經常出現下面的說法：

數列1，3，5，7，…的通項公式是

(二)發現問題

對于教材、教輔和學生作業中的這些常見表述，許多教師已司空見慣其實，作為教師，特別是數學教師，其思維應該是嚴密的、合乎邏輯的仔細分析材料就會發現，從邏輯上講，上面的表述并不是完全一致的

材料一的題目中，要求寫出的是已知數列的“一個”通項公式，而材料一的解題過程中，通項公式的前面沒有寫出定語“一個”“一個”沒有寫出來，這重要嗎？有沒有影響呢？如果無關緊要，當然可以不寫；如果不能不寫，當然應該寫出來強調一下！材料二的題目中沒有出現“一個”二字，這樣表述可以嗎？到底對不對呢？顯而易見，上面兩種情況，說的是一回事，道理是一樣的

數學是思維的體操教師應該充分利用上面這些教學資源深入思考，同時有效引導學生深入研究，培養他們的思維能力反之，在數學教學中，如果我們習慣了或認可了上面的說法，時間長了，部分教師和學生便會形成這樣的認識：不管是什么樣的數列，只要給出了它的前幾項，它的通項公式都是唯一的因此，我們有必要對上面的問題做進一步探討

二、提出問題

深入思考可以發現，上面的問題與下面兩個問題本質上是一致的我們先來看日常生活中的例子：

濱江市第一高中只有一位正職校長，叫秦達；有三位副校長，分別是張三、李四和王五那么，我們既可以說秦達是濱江市第一高中校長，也可以說濱江市第一高中校長是秦達我們可以說張三是濱江市第一高中副校長，但不能說濱江市第一高中副校長是張三所以，不考慮邏輯，隨便說話，就容易犯錯

數學中類似的例子很多，比如“自然數的單位”這個問題以下面兩道判斷題為例，很多人在做這兩道題時，往往會掉入陷阱

(1)自然數的單位是1

( )

(2)1是自然數的單位

( )

第(1)題，“自然數的單位是1”這道判斷題是錯的，因為，自然數的單位不是唯一的，有個(一)，十，百，千，萬，十萬，百萬，千萬，億，…，所以我們可以說：

個(一)是自然數的單位，

十是自然數的單位，

一百是自然數的單位，

一千是自然數的單位

……

但是不能說：

自然數的單位是個(一)，

自然數的單位是十，

自然數的單位是一百，

自然數的單位是一千

于是，上面的第(2)題“1是自然數的單位”是正確的

從數學的角度看，雖然自然數的單位有很多，但是自然數的基本單位只有一個，那就是“1”所以，我們既可以說自然數的基本單位是1，也可以說1是自然數的基本單位

由此看來，給定數列的前幾項，如果根據這個數列前幾項的排列規律，只能唯一地寫出這個數列的以后各項，那么背景材料一的解題過程和背景材料二的題目中的“一個”就顯得不重要了，“一個”既可以寫，也可以不寫如果根據一個數列的前幾項，寫出的數列的以后各項不是唯一的，那么，前文所述的背景材料一的解題過程和背景材料二的題目中，“一個”就不能不寫了

于是，我們要研究的問題就變成：給定數列的前幾項，根據這個數列前幾項的排列規律寫出的這個數列的以后各項是否唯一

三、分析問題

因為數列的項形形色色，數列的個數有無窮多個，所以要直接回答“給定數列的前幾項，根據這個數列前幾項的排列規律寫出的這個數列的以后各項是否唯一”這個問題，就顯得十分困難需要從具體例子入手展開研究

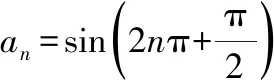
看到這里，讀者心里肯定會想：那么結論到底是什么？下面，我們就以數列2，4，8，…的通項公式為例進行研究

對于數列2，4，8，…，絕大多數同學會很快求得它的通項公式為=2

理由：因為=2,=4,=8，

所以這個數列是等比數列，且公比=2由等比數列的通項公式得

=·-1=2×2-1=2

從而得出數列2，4，8，…的通項公式是=2的結論

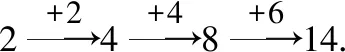
我們的結論是數列2，4，8,…的通項公式不是唯一的，=2只是它的一個通項公式，而它的通項公式還可以有其他形式

由此可見，背景材料一中，例題的說法沒有問題，問題在于，它的解題過程中漏掉了“一個”二字正確的解題過程如下：

此數列的前4項2，4，6，8都是項數的2倍，所以它的一個通項公式是=2

同樣，背景材料二的題目中，問題也是漏掉了“一個”二字題目應該改為數列1，3，5，7，…的一個通項公式是

四、解決問題

數列,,,,…,…從第二項起，每一項與它的前一項的差按前后次序，排成了一個新數列-,-,-…,+1-,…

前面那個新數列2，4，6，…可以看成一個公差為2的等差數列顯然，數列,,,,…,…與等差數列有一定的“血緣關系”，數列理論中把這樣的數列稱為二階等差數列為區別于二階等差數列，我們把通常定義的等差數列稱為一階等差數列那么二階等差數列的通項公式如何求呢？我們可以采用求等差數列通項公式的思路解決此問題

設數列,,，…,,…是一個二階等差數列，為了書寫的方便，我們把數列-,-,-，…,+1-,…簡記為

,,,…,,…

(1)

則數列(1)為等差數列，且有=+1-(≥1,∈)

設數列(1)的公差為，則

=-=-=…=+1-(≥1,∈)，

因此，=-=(-)-(-)=-2+

由于=+(-1)，

∴+1-=+(-1)，

即+1=++(-1)

依此規律，則有

=+，

=++，

=++2，

……

=-1++(-2)

把上面各式左右分別相加，得

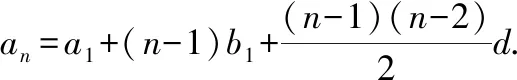
這就是二階等差數列的通項公式，其中，=-，

=-2+

我們來檢驗一下其正確性：

當=1時，=1-1+2=2；

當=2時，=2-2+2=4；

當=3時，=3-3+2=8；

當=4時，=4-4+2=14

完全正確！

這樣，上面得到的結論又進一步驗證數列2，4，8，…的通項公式不唯一=2是它的一個通項公式，此時，=2=16=-+2也是它的一個通項公式，此時=14那么以2，4，8為前3項的數列，通項公式到底有幾個呢？2個，3個，……，還是無數個？

要回答這個問題，我們還是用事實加以證明有人說，=-5+10-4也是它的一個通項公式，對不對呢？

我們來代入檢驗：

當=1時，=1-5×1+10×1-4=2；

當=2時，=2-5×2+10×2-4=4；

當=3時，=3-5×3+10×3-4=8；

所以，=-5+10-4確實是數列2，4，8，…的一個通項公式，只不過這時=4-5×4+10×4-4=20(注意，這時通項公式是的3次方的形式，原數列已經變成三階等差數列了)

綜上所述，我們不難得出結論：以2，4，8為前3項的數列通項公式不唯一如果把=2當作一個通項公式，第4項就是16；如果把=-+2當作一個通項公式，第4項就是14；如果把=-5+10-4當作一個通項公式，第4項就是20通項公式不同，第4項也不同如果我們大膽假設第4項為任意給定的一個實數，是否能得到這個數列的一個通項公式呢？因為2，4，8，是4個已知數，我們不妨把通項公式設成4個參數的形式

已知數列為2，4，8，，…

設它的一個通項公式為=+++

其中，,,,為待定系數把=1,2,3,4代入，得方程組如下：

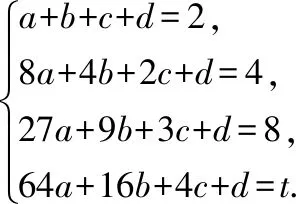
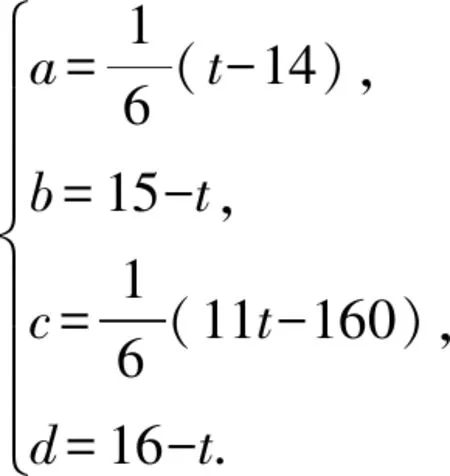
這樣，每給出一個值，就可以求得相應的,,,，從而得到所給數列的一個通項公式

事實上，=14時，=0,=1,=-1,=2，這正是前面的通項公式=-+2；當=20時，=1,=-5,=10,=-4，這正是前面的通項公式=-5+10-4

由于可以取任意實數，這樣就有無窮多組,,,的值滿足條件，所以，以2，4，8為前3項的數列的通項公式有無窮多個每給定第4項的一個值，就可以得到一個通項公式不過，這里得到的無窮多個通項公式，都是用項數的三次多項式表示的，并不包括用其他形式(如用指數形式2)表示的通項公式因此，要寫全所有的通項公式是辦不到的可見，無論是出題還是解題，“一個”二字千萬不能漏寫

五、總結反思

一般而言，使用省略號時應明確所省略的各項是按照什么規律排列的這里只給出數列的前三項，而沒有明確其后面省略的各項，即沒有說明從第四項起以后的各項所遵循的規律，由于第四項的不同，可以得到無窮多個滿足前三項要求的通項公式同樣，第四項相同而沒有明確用什么規律來確定第五項，還是可以得到無窮多個通項公式以此類推，我們可以得出一個共同的結論：只給出前若干項的數列，總可以得到無窮多個通項公式

在教學實踐中，我們應該形成這樣一種共識：如果出題者的意圖是求等比數列的通項公式，那么應當在題目中加上“等比數列”這一條件，即題目應改為“已知等比數列2，4，8，…，求這個數列的通項公式”這時省略號所省略的各項，可按等比數列的規律逐一寫出，它的通項公式就是=2

同樣道理，求數列1，3，5，…的通項公式，省略掉的規律也不具體，因此也有無窮多個滿足前三個條件的通項公式，如=-6+13-7就是其中之一如果題目是考查求等差數列的通項公式，那么應加上“等差數列”這一條件

對于自然數列，應寫成自然數列1，2，3，…

有些數列沒有特殊的名稱，那么應寫出它的通項(也就是一般項)以表示所省略的各項的規律例如：

1·2,2·4,3·8,…,·2,…;

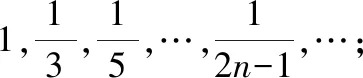
1·2·3，2·3·9，3·4·27，…，·(+1)·3,…

當然，一些教科書考查的是學生通過觀察來發現由所給數列的前幾項找出熟知的規律，從而能依次寫出以后的各項，進而寫出它的通項公式的能力，如：

2,4,8,…;