基于改進PSO算法的B樣條曲線擬合*

李軒宇, 張兆軍, 許釗雄

(江蘇師范大學 電氣工程及自動化學院,江蘇 徐州 221116)

0 引 言

現代工程設計中經常需要從測量的數據點中獲取最合適的曲線或曲面表達,但這些數據點往往由于各種因素的影響存在誤差,所以待求的曲線或曲面不必嚴格地經過每一個數據點,可以用擬合的方法逼近數據點。由于B樣條曲線具有較好的逼近能力以及局部修改等優秀的數學性質[1],可以靈活表示各類曲線及曲面的形狀。因此,在測試數據處理、逆向工程和圖像處理[2,3]等工程領域中,B樣條曲線擬合技術得到了廣泛的應用。

國內外學者對于B樣條曲線擬合問題已經做了大量的研究。Bo P等人[4]在充分考慮曲線形狀特征的基礎上提出一種基于圖形的平面相交B樣條曲線擬合方法。Deng C等人[5]使用漸進迭代逼近的方法求解數據點數量較大的擬合問題,具有較好的保形效果。利用各種智能算法求解曲線擬合問題是一個新的研究方向。胡良臣等人[6]提出一種基于二進制遺傳算法的B樣條曲線擬合方法,可以在滿足法向約束條件的同時生成誤差較小的擬合曲線。Uyar K等人[7]采用雜草優化方法選擇最優節點進行B樣條曲線擬合,實驗結果表明了較好的擬合效果。節點向量的選擇對于曲線的擬合效果具有重要影響,合適的節點向量可以減小曲線擬合誤差。粒子群優化(particle swarm optimization,PSO)算法[8]在求解曲線擬合問題時存在早熟收斂,易于陷入局部最優等缺點。

本文結合遺傳算法(GA)[9]和天牛須搜索(BAS)策略[10]對標準PSO算法進行改進,提出一種基于GA-BAS策略的改進粒子群優化(genetic-beetle PSO，GBPSO)算法用于求解帶法向約束的3次B樣條曲線擬合問題。

1 問題描述

1.1 數學模型

一條p次B樣條曲線可以表示為

(1)

式中p為B樣條曲線次數,本文取p=3；Pi為控制頂點；Ni,p(u)為p次B樣條在節點向量U上的基函數,定義如下

(2)

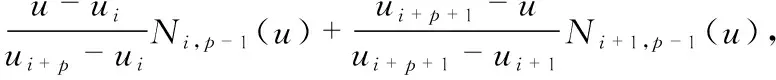
p≥1

(3)

式中 規定0/0=0；ui,i=0,1,…,n+p+1為節點向量U{ui}中的元素,u的范圍一般取[0,1]。

給M+1定個數據點dk和法向約束條件lk,找到一條曲線C來逼近數據點dk的同時要滿足數據點處的法向約束條件lk。文獻[6]中將此類問題轉化為帶等式約束的最小化問題,即

式中tk為數據點dk所對應的參數值；‖·‖為平方范數；C′(tk)為曲線在tk處的一階導數。

對于優化模型式(4),利用罰函數方法將其轉換為無約束最優化問題,建立適應度函數如下

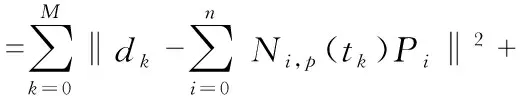
(5)

式(5)為本文最終所要優化的適應度函數,并利用GBPSO算法對其進行優化求解。

1.2 數據點參數化方式

求解曲線擬合問題時首先要將數據點進行參數化,不同的參數化方法會影響曲線最終的擬合效果。均勻參數化、向心參數化和弦長參數化是三種常用的參數化方法。本文中擬合曲線會面臨數據點急劇變化的情況,因此選擇向心參數化,該方法在處理此類問題時效果更好。參數tk與數據點dk的關系如下

(6)

2 算法介紹

2.1 PSO算法原理簡介

PSO算法首先初始化產生N個粒子,每個粒子代表優化問題的一個潛在解。粒子i的速度和位置分別用d維向量vi和xi表示。粒子通過迭代更新自己的速度和位置,更新方式如下

(7)

(8)

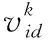
2.2 BAS算法[10]簡介

BAS算法是一種新型智能優化算法[10]。天牛在覓食過程中不知道食物的確切位置,僅依靠兩個觸須探測食物氣味并通過判斷左右須氣味濃度大小來決定下一步的走向。如果左須氣味強于右須,則向左移動,反之向右移動,直至找到食物。其數學模型如下：

1)隨機天牛的搜索方向并標準化

(9)

式中 rands(·)為隨機函數；n為空間維度。

2)計算左右須坐標

(10)

式中xlt和xrt分別為天牛左右須在t時刻的位置；d0為兩須之間的距離。

3)根據兩須對應的函數值,決定天牛下一步位置

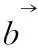
(11)

式中δt為t時刻的步長；f為目標函數；sign(·)為符號函數；f(xlt)>f(xrt)時取-1,反之為1。

BAS算法僅僅通過單一個體進行尋優,具有較好的局部搜索能力,但也因此缺乏個體之間的信息交互,導致算法的全局搜索能力較弱。

2.3 GBPSO算法流程

由于標準PSO存在易于陷入局部最優的缺點,而BAS算法在局部搜索方面具有優勢。本文首先結合兩種算法的優點,將BAS策略引入到PSO算法之中,提高單個粒子的尋優能力幫助算法跳出局部最優,然后通過交叉和變異操作提高子代種群的多樣性,增強算法的全局搜索能力,基于此提出一種改進的粒子群算法GBPSO。

GBPSO算法中,每個粒子都被當成一個個的天牛進行尋優。與標準PSO相同的是,粒子的初始位置采用隨機初始化策略,速度使用式(7)進行更新。不同之處在于,粒子的位置更新中結合了BAS策略,按式(12)更新

(12)

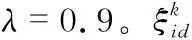
增量函數ξ的計算公式如下

(13)

式中δk為天牛在第k次迭代時的步長；Xld和Xrd為天牛的左右須坐標,其更新公式如下

(14)

步長δ隨著迭代衰減,本文初始步長設為1,δ和搜索距離s之間有如下關系

δk=eta·δk-1

(15)

sk=δk/T

(16)

常量eta和T的值根據經驗進行調整,本文取eta=0.95,T=2。

本文選擇交叉方式為均勻交叉,交叉概率pc=0.5。變異方式選擇高斯變異,變異概率pm=0.05。

算法的具體步驟如下：

Step1 初始化種群和速度并設置相關參數。

Step2 計算每個粒子(天牛)的適應度值。

Step3 對每個粒子,比較其當前適應度值和pbest的大小,如果當前解更小,則更新pbest。

Step4 對每個粒子,比較其當前適應度值和gbest的大小,如果當前解更好,更新gbest。

Step5 通過式(7)對粒子的速度進行更新。

Step6 根據式(14)得到天牛左右須坐標,并計算左右須的適應度值。

Step7 根據式(13)更新增量函數ξ,并結合式(12)更新粒子位置。

Step8 對子代個體進行交叉和變異操作,經過篩選得到更加優秀的子代個體。

Step9 若滿足中止條件則退出算法,否則返回Step2。

2.4 基于GBPSO的B樣條曲線擬合算法

通過罰函數方法將帶法向約束的B樣條曲線擬合問題轉化為無約束最優化問題。算法流程如圖1所示。

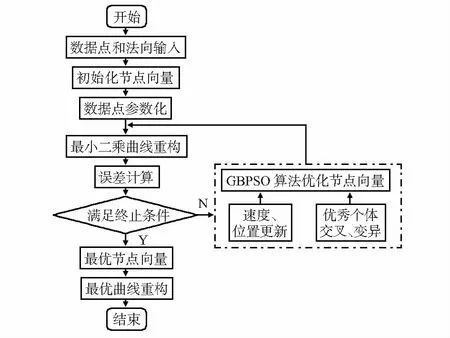
圖1 B樣條曲線擬合流程

3 實驗仿真

3.1 擬合曲線選擇

本文選擇了4個不同類型的算例,其表達式以及定義域如表1所示。

表1 算例詳細信息

每個算例的取點間隔為0.05,則例1的取點個數為80,例2～例4的取點個數均為126。例4中參數a=1,b=1/2,h=1。

3.2 實驗說明

本文選擇4個算例驗證所提GBPSO算法的擬合效果,并通過與標準PSO[8]和另外兩種改進PSO算法—結合BAS的PSO(beetle PSO，BSO)[11]、和結合GA的PSO(GAPSO)[12]對比來證明其有效性。每組實驗在相同條件下獨立運行20次,以適應度值為擬合效果的評價標準,統計20次實驗結果的最大值、最小值、平均值和方差。

GBPSO算法與3種對比算法的參數設置見表2。表2中sizepop表示種群規模,maxgen表示算法的最大迭代次數。

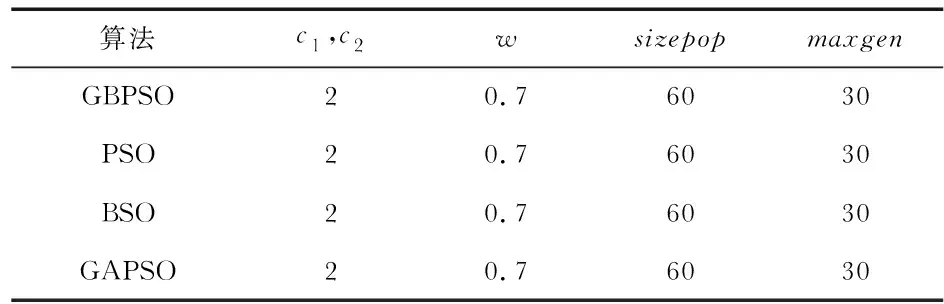
表2 算法參數設置

3.3 實驗結果與分析

圖2所示為GBPSO算法優化節點向量的曲線擬合效果圖。由圖2可以看出,本文所提GBPSO算法對所有4個算例都具有較好的擬合效果。

圖2 4個算例的擬合效果圖

圖2(a)中曲線形狀較為簡單,GBPSO算法在處理此類問題時可以達到較好的效果。圖2(b)和圖(d)中曲線的數據點分布較為均勻,且圖2(d)存在曲線交叉的情況,可以看出GBPSO算法對解決此類問題也是可行的。圖2(c)中曲線不僅存在交叉的情況,而且在局部有著較為尖銳的變化。可以看出,GBPSO算法不僅在處理平滑曲線時有較好的效果,而且在面對曲線形狀急劇變化的復雜情況時,依然能夠得到理想的擬合曲線。擬合仿真實驗結果表明,所提GBPSO算法在面對一般的情況時,不僅可以得到誤差較小的擬合曲線,且能夠滿足數據點處的法向約束條件。

為了進一步說明本文改進算法的有效性,GBPSO算法與三種對比算法對以上4個算例的數值實驗結果見表3,加黑數值表示算法在相應算例上的最優結果。

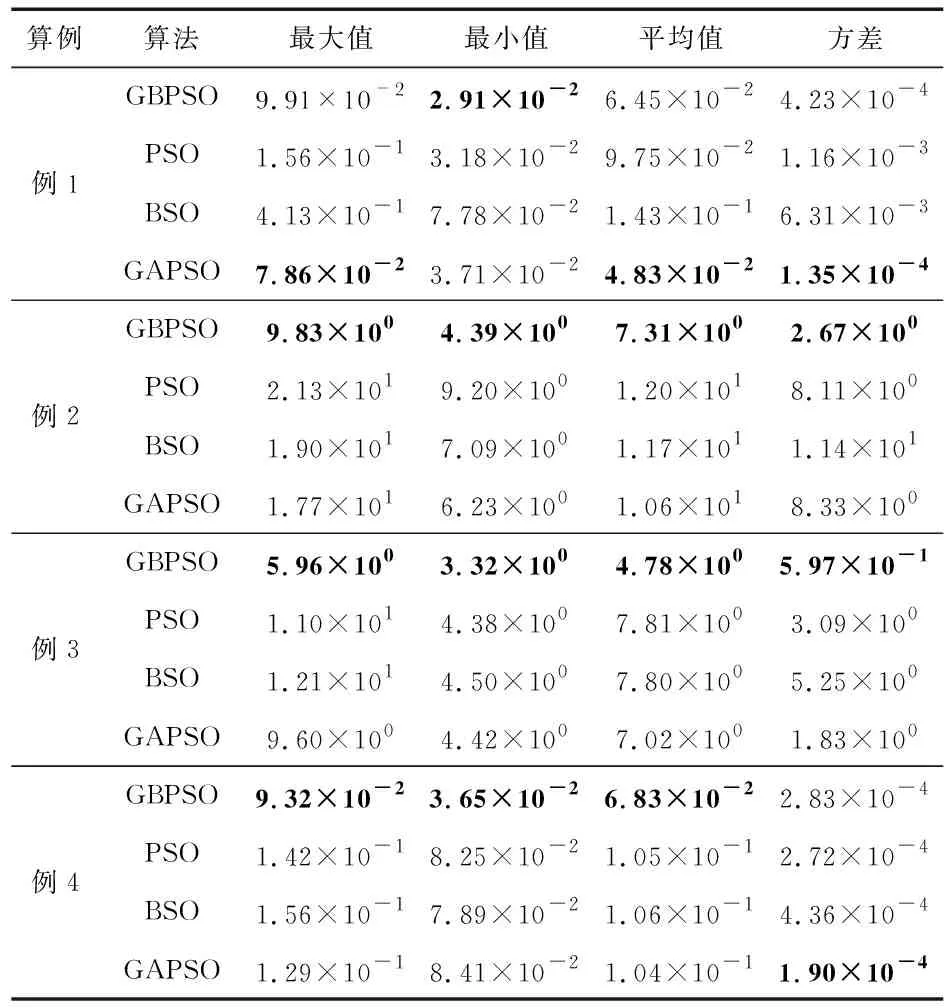
表3 數值實驗結果

由表3可以看出,對于所給的4個算例,本文所提GBPSO算法的優化結果都要優于標準PSO算法,同時在例2～例4三條曲線的表現上優于BSO和GAPSO兩種算法。對于算例1,由圖3可以看出該曲線形狀較為簡單,因此,所提算法與GAPSO算法在尋優結果上差別很小,都在同一數量級,而從最小值的統計結果來看,所提GBPSO算法有一定的能力找到比GAPSO更好的解。

4 結 論

本文基于遺傳算法和天牛須搜索策略提出了GBPSO算法用于求解數據點帶法向約束的B樣條曲線擬合問題。不同于標準PSO算法,GBPSO中通過BAS策略更新粒子位置,并結合GA中的交叉和變異操作保證子代種群的多樣性,增強算法的全局搜索能力。通過罰函數的方法將帶法向約束的B樣條曲線擬合問題轉換為無約束最優化問題,然后利用GBPSO對節點向量的位置進行優化。實驗結果表明,本文算法生成的擬合曲線不僅誤差較小,而且能夠滿足數據點處的法向約束條件。