緊扣數學知識本質 促進學生深度學習

王火炬

深度學習區別于淺層學習，其培養目標指向培養學生的高階思維，在情感維度方面，教師應更注重調動學生全身心參與;在具體實施策略上，教師應注重知識的系統化和結構化，采用多種手段呈現良好的課堂氛圍。在數學教學中，教師要促發學生深度學習，除了根據上述兩個維度實施相應的策略外，還應該緊緊扣住數學知識的本質，才能使深度學習更真切地發生，才能使數學教學不僅有效度，而且有深度和廣度，最終促使學生真正獲得數學知識、關鍵能力和核心素養。

一、引導“深究”，建構知識模型

“深究”就是要借助富有挑戰性的問題情境，引導學生深入思考與探究，而在探究的過程中立足于數學思維，借助幾何直觀、動手操作等手段，幫助學生把生活經驗抽象歸納成邏輯經驗，完成從舊知識到新知識的轉化，并建構知識模型。例如，在人教版三上“測量”這一單元的“厘米”相關內容的教學中，如果在課程的開始階段就讓學生拿出尺子，認識尺子上1厘米的長度，來幫助學生建立“厘米”的概念，這樣的課程過于抽象和呆板，且沒有抓住知識的本質。由于厘米和其他長度單位一樣，本質是度量單位，因此在教學時，可以引導學生在經歷度量的過程中體驗和認識厘米。教師可以通過創設如下富有挑戰性的問題情境形成問題串：“如下圖，兩條線段誰長、誰短？如何準確說出線段1比線段2長（或短）多少？你想用什么數量單位來表示這兩條線段的長度？”在引導學生探索和解決一個個問題的過程中，幫助學生建立1厘米的概念。緊接著引導學生結合尺子認識2厘米、7厘米等其他長度，讓學生說一說2厘米、7厘米等各表示幾個1厘米，并讓學生動手比劃，完善“厘米”的認知。

在小學數學的課程教學中，教師應注重調動學生的多種感官，引導學生投入身心，充分體驗。例如在人教版五下“質數和合數”的教學中，教師要緊緊抓住質數和合數的本質區別，借助幾何直觀，設置出如下具有一定挑戰性的問題：“請你分別畫出面積為2、3、4、5、6、7的所有長方形（邊長均為整數），觀察一下，說出自己的發現。”在學生動手操作和觀察討論后，引導他們歸納出結論：面積2、3、5、7的都只能畫出一個長方形，它們的邊長都為1和等于面積的數;4和6則不止畫出一個，不僅能畫出邊長為1和等于面積數的長方形，還可以畫出邊長分別為2和2、2和3的長方形，所畫出的長方形邊長都是面積數的因數。隨后，教師讓學生再舉出關于質數與合數的其他例子，進一步拓展建模，引導歸納出質數和合數的概念。如此教學，不僅滲透數形結合思想，同時緊扣知識本質，調動學生的多重感官，促進學生更好地探究知識的本質，最終形成質數和合數的概念。

二、把握“深化”，搭建知識體系

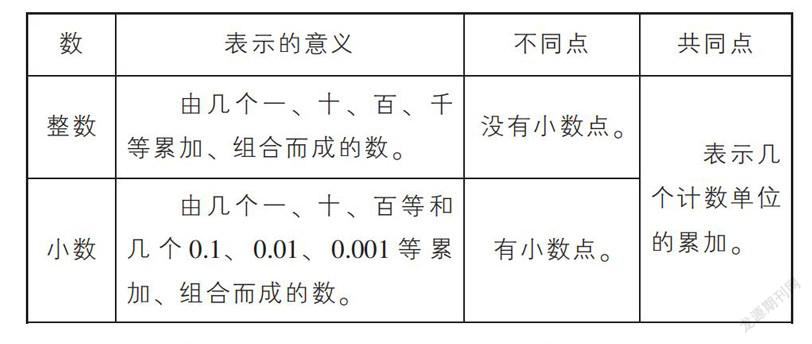
數學學科的知識之間存在著千絲萬縷的聯系，引導學生學習、體驗知識結構，實際上是對知識學習的深化。教師應當尋找到知識間的內在聯系，把相關聯的知識結構化，形成知識體系，避免知識的碎片化、零散化、無序化。具體到教學中，在避免淺層建構的同時，深入挖掘知識的本質，這樣搭建起的知識體系才能使學生對其理解得更加深刻。例如，在學習了人教版三下“小數的初步認識”之后，如果只是讓學生認識到整數和小數的相同點都是數，不同點是小數有小數點、整數沒有小數點，這樣建構起來的聯系未免顯得淺薄。教師可以安排類似的課堂練習：“分別說出數23、456、0023、9、0.5、4.56表示幾個幾？請在認真思考后進行觀察和分類，你有什么發現？”通過這樣的練習，引導學生建立小數和整數的知識結構，即小數和整數一樣，本質上都是幾個計數單位的累加，最終與學生共同制成該知識結構的表格形式（如下表）。

三、指導“深解”，感悟知識的內涵外延

任何數學知識的存在都有其意義，數學知識的產生亦然。教師應注重引導學生運用最真切的感受將學到的數學知識、建構的數學模型，用于解決生活中的實際問題。在具體應用中，教師一定要抓住知識的本質，設計與知識相對應的問題讓學生解決，并讓其在解決過程中進一步理解和感受知識的內涵與外延，深化對知識模型的應用。如果解決問題的過程沒有扣緊知識的本質，就會出現純粹為了運用而運用或者簡單套用公式的情形，使學生無法獲得深刻的認知。例如，在人教版五上“植樹問題”一課的教學中，筆者先引導學生通過課本中的情境建立解決植樹問題的模型：總長度÷間距=間隔數，然后分三種類型建立數量關系：兩端都種樹用“棵數=間隔數+1”，只種一端用“棵數=間隔數”，兩端都不種用“棵數=間隔數-1”。模型建立后一般要讓學生運用所學模型解決實際問題，教學中如果只是按部就班地出示如下問題：“在長1千米的道路兩邊種樹，每隔50米種一棵（兩端都種），一共要種多少棵？”面對這樣的問題，學生只需要機械地套用模型公式即可，并沒有深入知識的本質。因此，筆者緊密結合生活實際設計出如下兩道課堂練習。首先出示練習題：“在長1千米的大橋兩側安裝路燈，每隔50米安裝一盞，且兩端都要安裝，一共要準備多少盞路燈？請你說出該問題中與植樹問題相對應的距離、間距、間隔數、棵樹各是什么？該問題應該運用哪種植樹類型？說說為什么。”待學生成功解答后，筆者接著安排另一道練習題：“木工師傅鋸一段木料，鋸4段用6分鐘，鋸成9段用時幾分鐘？請你嘗試用植樹問題的模型來解決，然后說出在該問題中與植樹問題相對應的距離、間距、間隔數和植樹類型。”植樹問題的本質是棵數與間隔數的對應關系，教師在新課教學中應注重對該知識點的呈現，促使學生理解和掌握，在課后練習中也應進行專項訓練，同時聯系生活設計與生活相關的實際問題，讓學生運用數學模型進行解決，從而達到舉一反三的目的。又如，人教版三上“集合”一課中，其知識的本質是分類組合，特別要關注兩邊的類屬關系，即重合部分，引導學生理解重合部分與總數之間的關系，并強調具體運用時不能重復計算。在教學進程中根據是否有重合的情況，教師可以在課件中呈現三種類型的集合圖。建立集合圖的模型就是要引導學生充分體驗，厘清有沒有重合，重合的部分是哪些。當幫助學生建立三種集合圖的模型后，可以安排針對性的練習題進行課堂訓練，讓學生辨別可以運用哪一種集合圖，說說為什么，重合的部分是什么，并說說解決問題時要注意些什么，讓學生通過實際問題再次明確重合部分與總數之間的關系，以及重合部分不能重復計算的注意事項。

（作者單位：福建省廈門市同安區第一實驗小學）