函數(shù)單調(diào)性討論中參數(shù)分類標準的確定
福建省德化第一中學(xué)吳志鵬(362500) 吳志鵬
討論函數(shù)的單調(diào)性?等價于分析其導(dǎo)函數(shù)的正負性,通過解不等式獲得原函數(shù)的增、減區(qū)間,確定其單調(diào)性,但是在解不等式的過程中經(jīng)常會與“參數(shù)”狹路相逢,面對“參數(shù)”,很多學(xué)生表現(xiàn)出無能為力,討論起來很困難,究其原因是找不著分類的標準,稀里糊涂的,找不著北.那么如何能做到準確分類?①熟悉模型,確定分類的標準,做到有根有據(jù); ②在定義域內(nèi)進行分類討論,做到“不重復(fù)也不遺漏”.下面就分類標準的確定作進一步的闡述:
類型一:導(dǎo)函數(shù)含有確定值域的函數(shù)式
若導(dǎo)函數(shù)含有如x2,ex等確定值域的式子,對于此類含參式子的討論,我們可根據(jù)多個非負實數(shù)式子的和為非負實數(shù)或多個非正實數(shù)式子的和為非正實數(shù),確定分類標準,如:
例1 (2020 高考全國卷文科節(jié)選)已知函數(shù)f(x)=x3?kx+k2,討論f(x)的單調(diào)性.
評析由于f′(x)=3x2?k,導(dǎo)函數(shù)中3x2≥0,根據(jù)兩個非負實數(shù)式子的和仍為非負實數(shù),只需讓?k≥0 即k≤0,此時f′(x)≥0,所以f(x)在(?∞,+∞)上單調(diào)遞增;而當k >0 時,則通過解不等式f′(x)=3x2?k >0 或f′(x)=3x2?k <0 得函數(shù)的增區(qū)間或減區(qū)間,確定函數(shù)的單調(diào)性.即本題中參數(shù)k可按k≤0 和k >0 進行分類.
解析當k≤0 時,f′(x)≥0 恒成立,所以f(x)在(?∞,+∞)上單調(diào)遞增; 當k >0 時,令f′(x)=0,得x=,令f′(x)<0,得?< x <令f′(x)>0,得x ,所以當k≤0 時,f(x)在(?∞,+∞)上單調(diào)遞增; 當k >0 時,f(x)在上單調(diào)遞減,在,上單調(diào)遞增.
同型題(2021年高考全國卷節(jié)選)已知函數(shù)f(x)=alnx+x2(a∈R,且a≠0),討論函數(shù)f(x)的單調(diào)性.

例2 (2017年高考全國卷理科節(jié)選)已知函數(shù)f(x)=ae2x+(a?2)ex?x,討論f(x)的單調(diào)性.
評析f(x)的定義域為(?∞,+∞),f′(x)=2ae2x+(a?2)ex?1=(aex?1)(2ex+1),因?qū)Ш瘮?shù)中2ex+1>0,所以我們只需討論aex?1 的符號即可,由ex >0,利用兩個非正數(shù)的和為非正數(shù),則當aex非正時,其與?1 的和為負數(shù),此時選取a≤0,從而確定參數(shù)a的討論標準,分為a≤0和a>0 兩類進行.
解析(ⅰ)若a≤0,則f′(x)<0,所以f(x)在(?∞,+∞)單調(diào)遞減.
(ⅱ)若a >0,由f′(x)=0 得x=?lna.當x∈(?∞,?lna)時,f′(x)<0; 當x∈(?lna,+∞)時,f′(x)>0.所以,當a≤0,f(x)在(?∞,+∞)單調(diào)遞減; 當a >0 時f(x)在(?∞,?lna)單調(diào)遞減,在x∈(?lna,+∞)單調(diào)遞增.
例3 (2017年高考全國卷文科節(jié)選)已知函數(shù)f(x)=ex(ex?a)?a2x,討論f(x)的單調(diào)性.
評析函數(shù)f(x)的定義域為(?∞,+∞),f′(x)=2e2x?aex?a2=(2ex+a)(ex?a),此時導(dǎo)函數(shù)中ex >0,而兩個式中的a與?a的符號恰好相反,若a >0 則2ex+a >0,我們只需討論ex?a的符號即可,從而確定參數(shù)a的分類標準,分為a<0,a=0 和a>0 三類情況.
解析函數(shù)f(x)的定義域為(?∞,+∞),f′(x)=2e2x?aex?a2=(2ex+a)(ex?a),
①若a=0,則f′(x)=2e2x >0,在(?∞,+∞)單調(diào)遞增;
②若a >0,則由f′(x)=0 得x=lna,當x∈(?∞,lna)時,f′(x)<0; 當x∈(lna,+∞)時,f′(x)>0,所以f(x)在(?∞,lna)單調(diào)遞減,在(lna,+∞)單調(diào)遞增.
③若a <0,則由f′(x)=0 得x=ln(?a/2),當x∈(?∞,ln(?a/2))時,f′(x)<0;當x∈(ln(?a/2),+∞)時,f′(x)>0,故f(x)在(?∞,ln(?a/2))單調(diào)遞減,在(ln(?a/2),+∞)單調(diào)遞增.所以當a=0 時,f(x)在(?∞,+∞)在單調(diào)遞增; 當a >0 時,所以f(x)在(?∞,lna)單調(diào)遞減,在(lna,+∞)單調(diào)遞增.當a <0時,f(x)在(?∞,ln(?a/2))單調(diào)遞減,在單調(diào)遞增.
類型二:導(dǎo)函數(shù)中存在含有參數(shù)的“二次三項式”
對于此類含參導(dǎo)函數(shù),討論起來稍微有點復(fù)雜,甚至有可能出現(xiàn)兩次確定分類標準,很多學(xué)生甚感“無能為力”,對于此類含參的多項式,若二次項系數(shù)含有參數(shù),首先我們得明確其為二次式還是一次式?確定首輪分類標準,即將二次式的系數(shù)以0 為標準進行分類,而對于二次式系數(shù)為常數(shù)的則只需解二次不等式f′(x)>0 或f′(x)<0,此時即把判斷二次不等式是否有解作為依據(jù),計算?≤0,得到參數(shù)的分類標準,此過程需結(jié)合二次項的系數(shù)的正負來確定,即根據(jù)函數(shù)圖象與x軸的交點情況進行討論.
例4 若函數(shù)f(x)=ax++lnx,討論函數(shù)的單調(diào)性.
評析f(x)的定義域(0,+∞),f′(x)=a?=,由于導(dǎo)函數(shù)是一個含參的分式,分母x2>0,即可設(shè)分子h(x)=ax2+x?2 為一個二次項含參的多項式,則此處的分類標準為式子是否是二次式?分為a=0 和a≠0 兩類;當a=0 解f′(x)>0 和f′(x)<0 得單調(diào)增(減)區(qū)間; 當a≠0 時,則需根據(jù)?≤0 和?>0 以及二次項系數(shù)的正負來確定參數(shù)的討論標準,當?=1+8a≤0即a≤?,結(jié)合二次項系數(shù)的正負可分為a≤?,
解析(1)當a=0 時,h(x)=x?2,所以當x∈(0,2),h(x)<0,即f′(x)<0,所以f(x)在(0,2)單調(diào)遞減; 當x∈(2,+∞),h(x)>0,即f′(x)>0,所以f(x)在(2,+∞)單調(diào)遞增;
(2)當a≠0,由于?=1+8a.
①若?=1+8a≤0,即a≤?時,在x∈(0,+∞)上,即h(x)≤0 即,f′(x)≤0,所以f(x)在(0,+∞)單調(diào)遞減;

由于導(dǎo)函數(shù)是一個含參的分式,分母x2>0.設(shè)h(x)=x2?ax+1,則分子h(x)為一個含參的二次多項式且二次項系數(shù)為常數(shù),此時可根據(jù)x2?ax+1=0 是否有解及解的情況來確定參數(shù)的分類標準,即按?≤0 及?>0 分類,可確定參數(shù)按a2 進行分類.
解析當?2≤a≤2 則f′(x)≤0,所以f(x)在(0,+∞)單調(diào)遞減.
當a >2,令f′(x)=0 得,x1=或x2=>0.且x1< x2; 當x∈(0,x1)和(x2,+∞)時,f′(x)<0; 當x∈(x1,x2)時,f′(x)>0.所以f(x)在(0,x1),(x2,+∞)單調(diào)遞減,在(x1,x2)單調(diào)遞增.當a
類型三:導(dǎo)函數(shù)中存在不確定大小的含參零點
對于此類導(dǎo)函數(shù),在分析不等關(guān)系時,首先要弄清零點是否在定義域內(nèi)?若零點均在定義域內(nèi),就是要判斷零點的大小,并以此為依據(jù)確定參數(shù)的分類標準.
例7 (2019年高考全國卷理科節(jié)選)已知函數(shù)f(x)=2x3?ax2+b,討論f(x)的單調(diào)性.
評析由于函數(shù)的定義域為(?∞,+∞),對函數(shù)求導(dǎo)得:f′(x)=6x2?2ax=6x(x?),此時的導(dǎo)函數(shù)在定義域內(nèi)存在兩個零點,即0 和,為了求解不等式f′(x)>0 或f′(x)<0,我們需要判斷兩根的大小,即0 和的大小,找到參數(shù)a的分類標準,即a <0,a=0 和a >0 三種情況進行討論.
解析(1)由
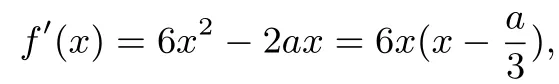
得到:當a <0 時,f(x)在上單調(diào)遞增,在上單調(diào)遞減,在(0,+∞)上單調(diào)遞增;當a=0 時,f(x)在R上單調(diào)遞增;當a>0 時,f(x)在(?∞,0)區(qū)間上單調(diào)遞增,在區(qū)間上單調(diào)遞減,在區(qū)間上單調(diào)遞增.
例8 求函數(shù)f(x)=(x?2)ex+(x?1)2+e(其中a∈R)的單調(diào)性.
評析易見,
f′(x)=(x?1)ex+a(x?1)=(x?1)(ex+a),
觀察導(dǎo)函數(shù)可知式子ex+a中的ex >0,依據(jù)兩個非負實數(shù)的和為非負實數(shù)可確定分類標準為a≥0 和a<0,當a≥0時,ex+a >0 恒成立; 而當a <0 時,ex+a=0 有根為x=ln(?a),此時需通過比較兩根的大小確定分類標準.
解析易見,
f′(x)=(x?1)ex+a(x?1)=(x?1)(ex+a).
(1)若a≥0 時,ex+a >0 恒成立,所以當x <1 時,f′(x)<0,f(x)單調(diào)遞減;當x>1 時,f′(x)>0,f(x)單調(diào)遞增.
(2)若a<0 時,令f′(x)=0 得x1=1 或x2=ln(?a);比較兩根可知:當a=?e 時,x1=x2; 當?e< a <0 時,x1>x2;當a
①當a=?e 時,x2=ln(?a)=1=x1,f′(x)≥0,f(x)在R 上單調(diào)遞增,如圖1.
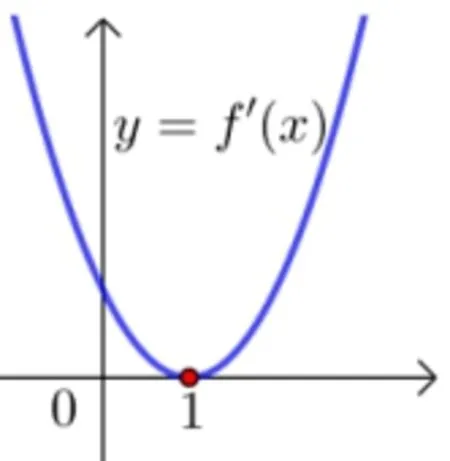
圖1
②若?e< a <0 時,x2=ln(?a)<1=x1,當ln(?a)< x <1 時,f′(x)<0,f(x)單調(diào)遞減;當x >1 或x
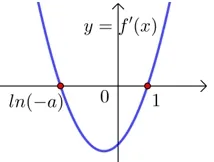
圖2
③若a 1=x1,當1< x
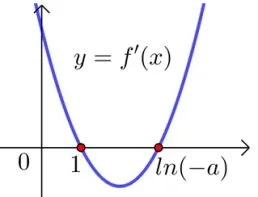
圖3
綜上所述,當a≥0 時,f(x)在(?∞,1)單調(diào)遞減,在(1,+∞)單調(diào)遞增; 當a=?e 時,f(x)在R 上單調(diào)遞增; 當?e< a <0 時,f(x)在(ln(?a),1)單調(diào)遞減,在(?∞,ln(?a)),(1,+∞)單調(diào)遞增; 當a
同型題(2021 全國高二單元測試)已知函數(shù)f(x)=ln+a2x2?ax,討論函數(shù)f(x)的單調(diào)性;
解析函數(shù)f(x)的定義域為(0,+∞),

通過分析導(dǎo)函數(shù)的符號,討論含參函數(shù)的單調(diào)性,其關(guān)鍵點是確定參數(shù)的分類標準,只有理清參數(shù)在函數(shù)中的意義,明白為什么要這樣分類,做到分類要有依有所據(jù),才能條理清晰,以上三類例題為我們學(xué)習(xí)函數(shù)單調(diào)性討論,參數(shù)分類標準的確定提供了有價值的示范.

