基于核凸非負矩陣分解算法的故障檢測方法
祝朋艷 徐進學 張學磊
(大連海事大學船舶電氣工程學院 遼寧 大連 116026)
Graph regularization constraints
0 引 言
隨著工業生產過程控制系統內部聯系越來越緊密,局部故障的發生往往影響整體的生產,造成較大的經濟損失。而大量傳感器以及智能儀器可隨時得到大量反映生產過程運行狀態的數據,通過分析采樣數據的特征信息,可尋找到適當的故障檢測方法。采樣數據一般具有高維、非高斯分布和非線性的特點。故障檢測主要包括降維和挖掘數據兩部分內容。對非線性數據來說,從高維空間中尋找一個更容易學習的低維嵌入不再是一種簡單的線性函數映射。核變換方法通過核變換將具有非線性結構的數據投影到一個核空間,在此空間中復雜的非線性數據可以實現線性化表示,從而進行降維[1],代表方法有核主成分分析(Kernel Principal Component Analysis,KPCA)[2]和核Fisher判別分析(Kernel Fisher Discrimination Analysis,KFDA)[3]。另外,故障檢測領域中常用到的主元分析法(Principal Component Analysis,PCA)[4]、偏最小二乘法(Partial least-squares,PLS)[5]和獨立主元分析法(Independent Components Analysis,ICA)[6]等多元統計方法可用于提取數據特征,其中ICA要求比較嚴苛不太適用于復雜的工業過程數據的處理。KPCA是核化后的PCA,能夠對非線性數據進行維數約簡,同時捕獲數據集的全局信息得以保留大部分的樣本特征,從而成為故障檢測領域中一種常用的多元統計方法。而實際過程中無論是描述一組數據集還是一幅圖像,都要選取其重要的局部特征加以分析,這些局部特征往往使得整個識別分析過程具有可解釋性,增加識別準確率。非負矩陣分解法(Non-negative matrix factorization,NMF)具有降維和提取局部特征的優點。考慮到原始數據不一定滿足非負的限制條件,多種NMF算法的變體應運而生,主要包括半非負矩陣分解法(Semi-NMF,SNMF)[7]、凸非負矩陣分解法(Convex-NMF,CNMF)[8]和凸包非負矩陣分解法(Convex-Hull NMF,CHNMF)[9]等。其中CHNMF選取數據集流形結構的極端點作為局部特征,使其不再受矩陣非負的條件約束,放寬了傳統NMF算法的應用范圍。另外,在局部信息的提取過程中,一般希望能夠盡量保持數據固有的幾何結構不發生改變,即數據集的大部分信息不隨矩陣分解過程而丟失。流行學習方法[10]廣泛應用于故障檢測領域,研究表明基于譜圖理論的非線性流行學習方法[11]可以保持數據變換過程中局部近鄰結構不發生改變。
通過分析核主元分析法(KPCA)與凸包非負矩陣分解方法的優勢所在,本文提出了核凸非負矩陣分解(KCNMF)算法,并測試了其有效性。該方法首先將原始采樣數據通過高斯核函數在高維空間中近似重構形成新的樣本矩陣,并利用PCA對重構數據進行白化處理。然后利用凸包非負矩陣分解算法對白化處理后的數據矩陣進行分解,找到能表示數據集群整體信息的局部特征,而圖正則化約束項則保證整個分解過程中數據分布的幾何結構不發生改變。最后利用分解得到的基矩陣建立N2和SPE統計量,求得控制限,在與控制限數值的對比中完成對測試數據的故障檢測。
1 核主元分析法
1.1 核主元分析法簡介
假設有一樣本矩陣Xm×n,有m個變量,而且每個變量有n個觀測值。本文選取z-score標準化方法對數據進行無量綱處理。對序列x1,x2,…,xn進行變換:
(1)

原始輸入空間中標準化后的樣本xk經非線性映射Φ:Rm→F,在高維特征空間F中重構表示為φ(xk)∈F。那么在空間F中φ(xk)的協方差矩陣為:
(2)
進一步在特征空間中執行PCA:
SFp=λsp
(3)
式中:λ為特征值;p是與λ相對應的特征向量。將特征值按以下順序排列λ1≥λ2≥…≥λn,取前d個特征值對應的特征向量作為PCA的主元方向。結合式(2)和式(3)得到:
(4)

在式(3)兩邊左乘映射向量φ(xk),形式如下:
〈φ(xk),SFp〉=λ〈φ(xk),p〉
(5)
聯合式(4)和式(5),化簡得到:
K2α=λsnKα
(6)
式中:K為核矩陣,(K)ij=k(xi,xj)=〈φ(xi),φ(xj)〉。
Kα=λkα
(7)
式中:λk=nλs。式(7)特征值分解運算后得到矩陣K的特征值λk,且進行降序排列λk1≥λk2≥…≥λkd,用下式選擇前q個最大特征值所對應的特征向量α1,α2,…,αq:
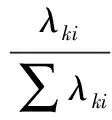
(8)
由此可計算特征空間中的特征向量P而得到主元方向。
1.2 特征空間數據白化
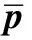
(9)
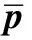
(10)
則白化后的樣本矩陣為:
(11)

2 算法設計
非負矩陣分解(Non-negative matrix factorization,NMF)算法用于提取數據中“有意義的”部分變量,描述了數據集的局部特征。非負性要求使得該算法所關注的部分變量只會經過加運算去重構原始樣本矩陣,特征之間不存在正負抵消的情況。用局部表現整體,分解過程簡潔高效,分解結果具有可解釋性是NMF算法的優點所在。
2.1 非負矩陣分解算法
設非負觀測數據矩陣V∈Rm×n,其中行向量表示樣本變量,列向量表示每個變量所包含的樣本。NMF方法對非負觀測數據V分解形式如下:
V=WHT+E
(12)
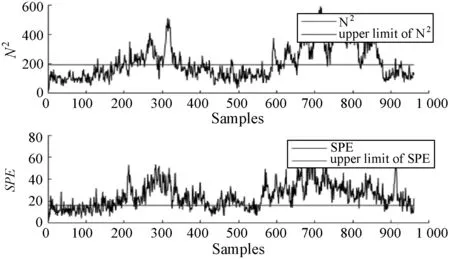
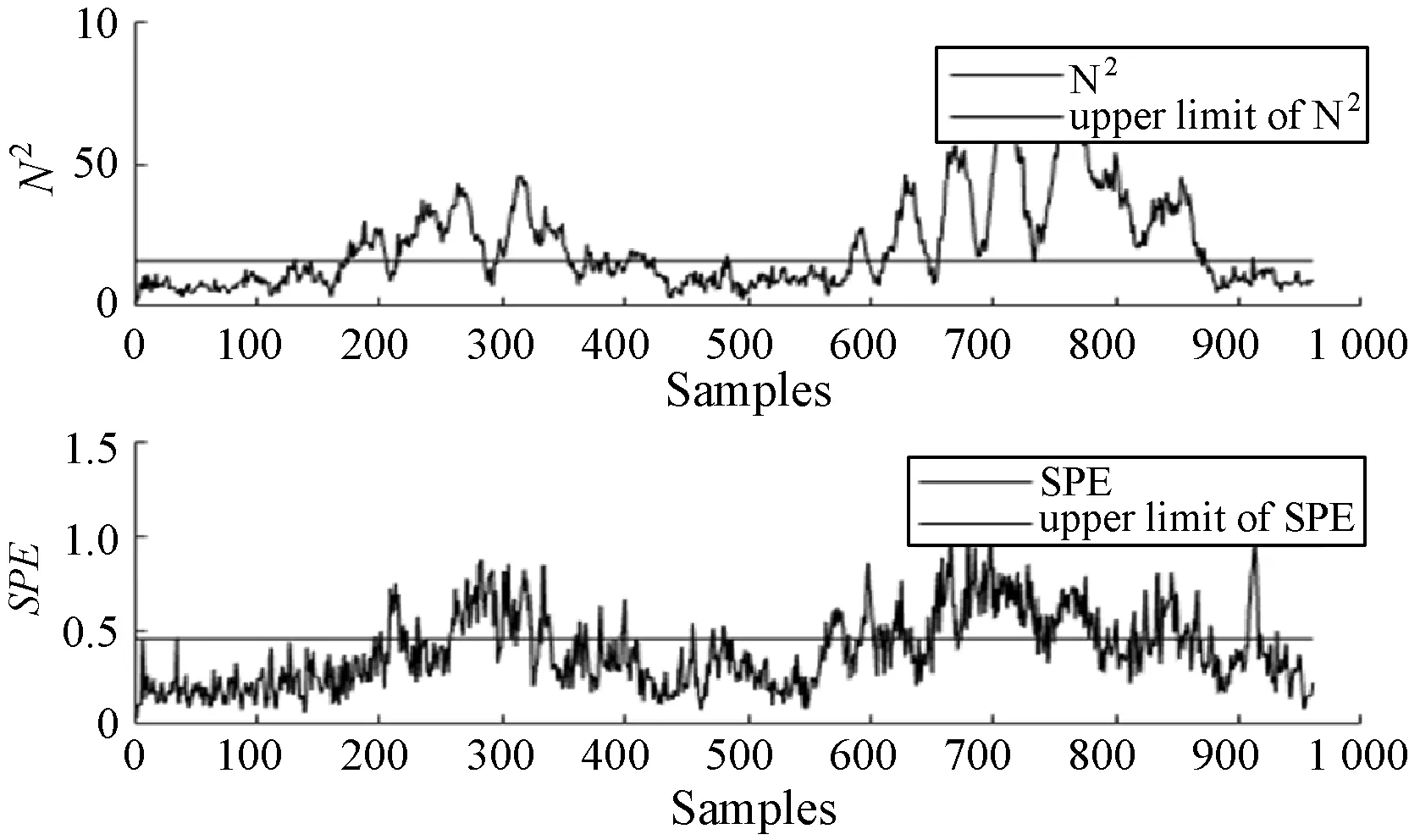
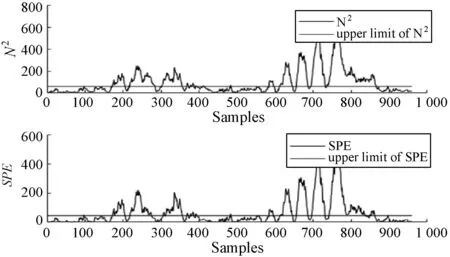
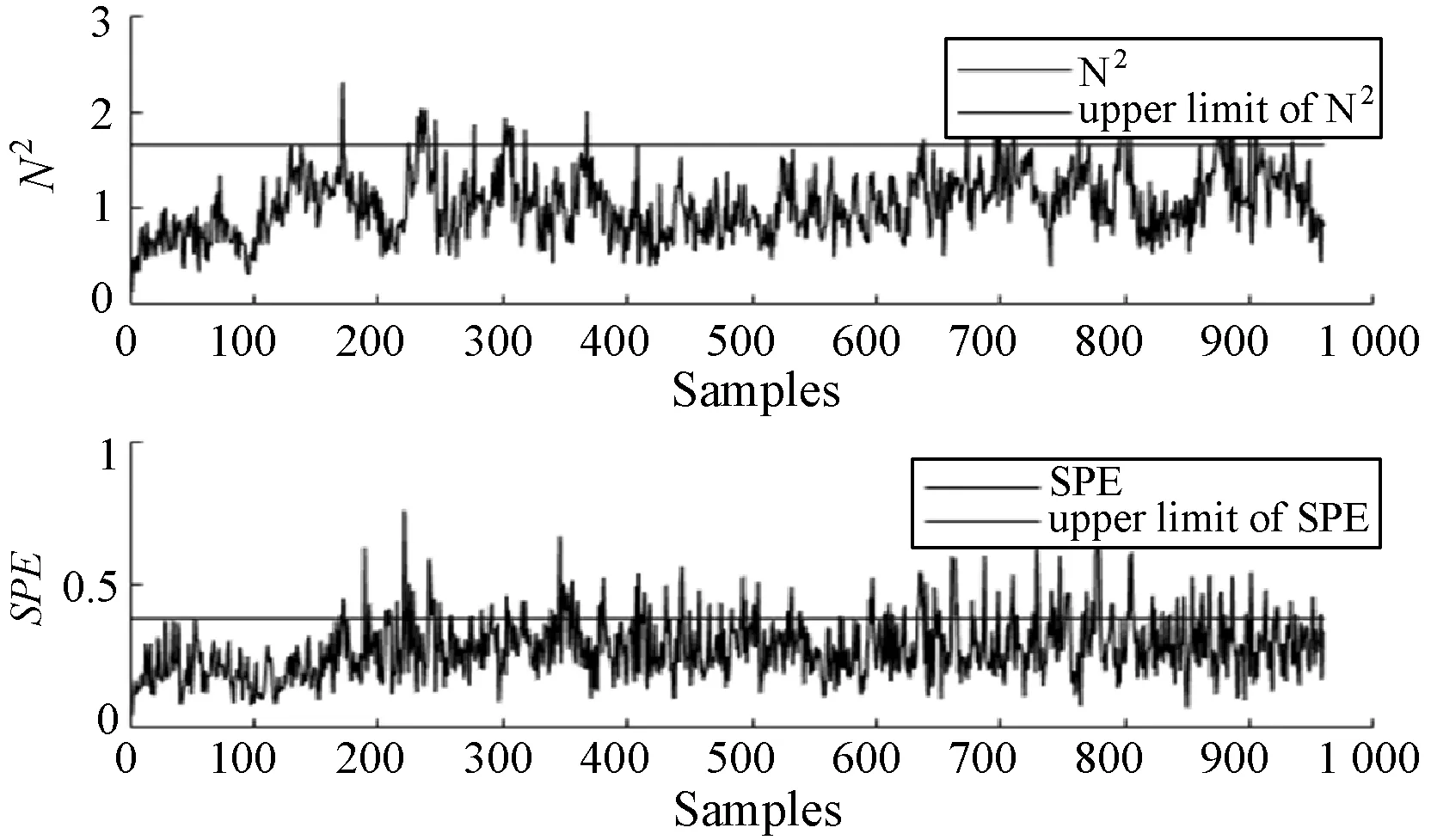
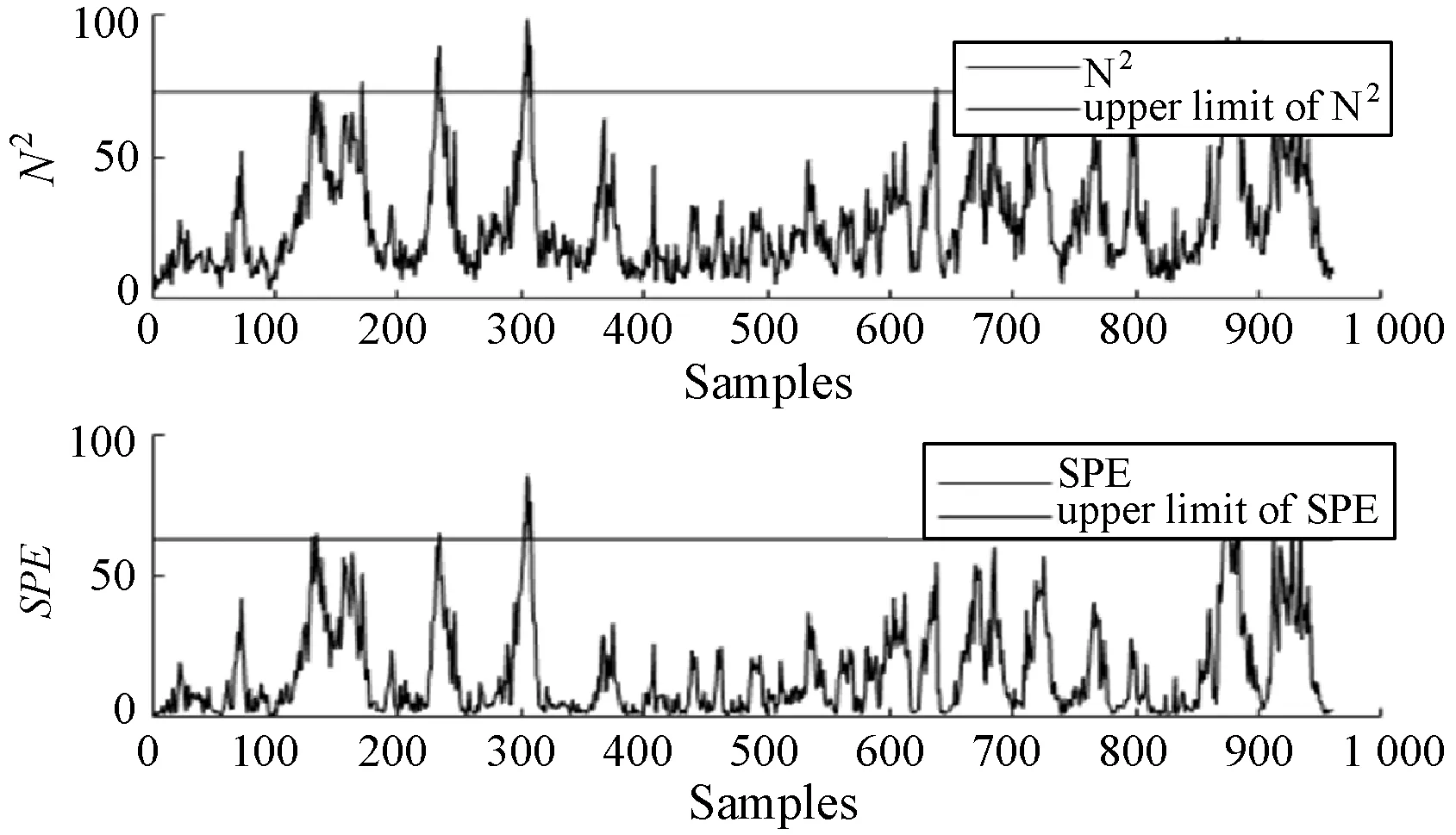
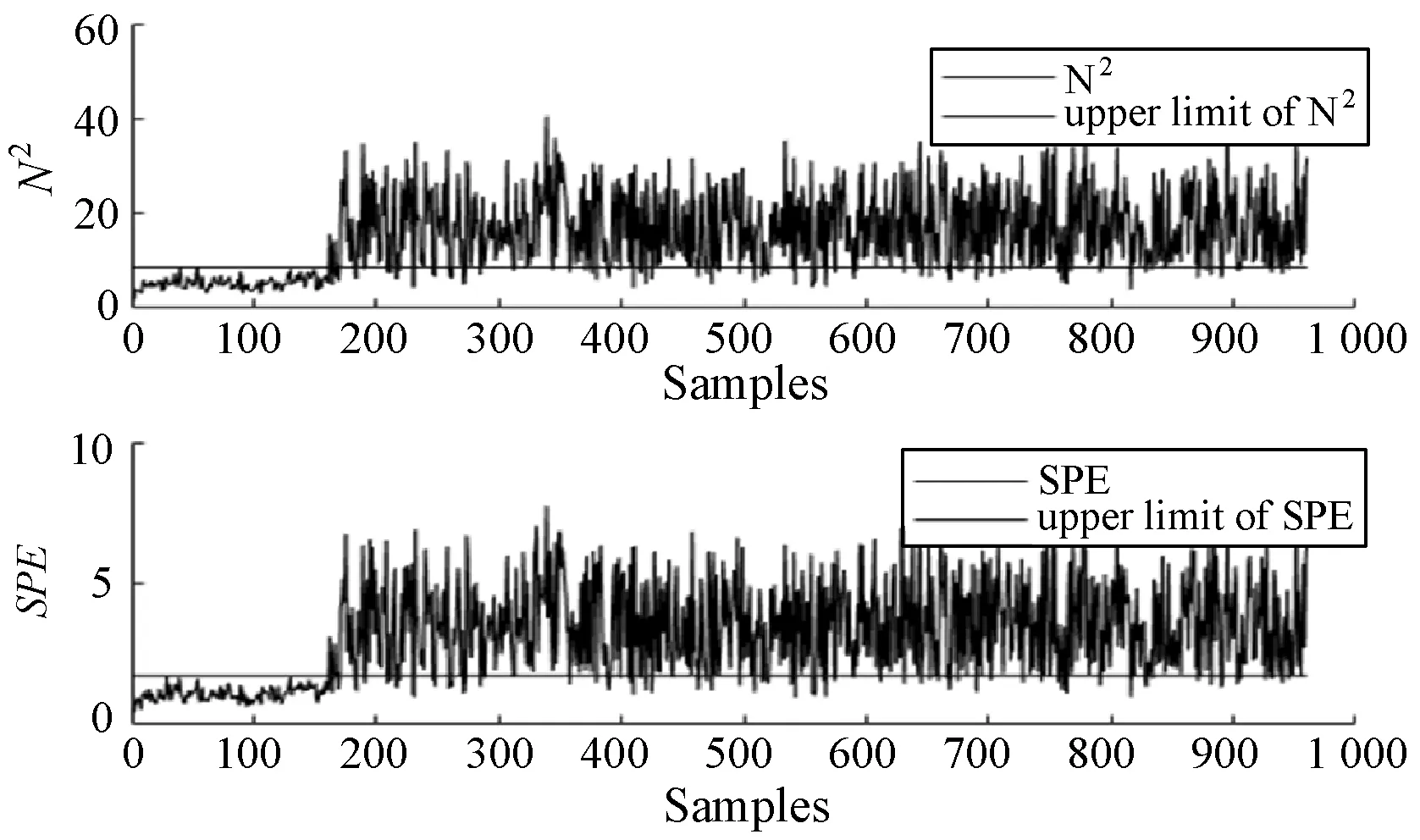
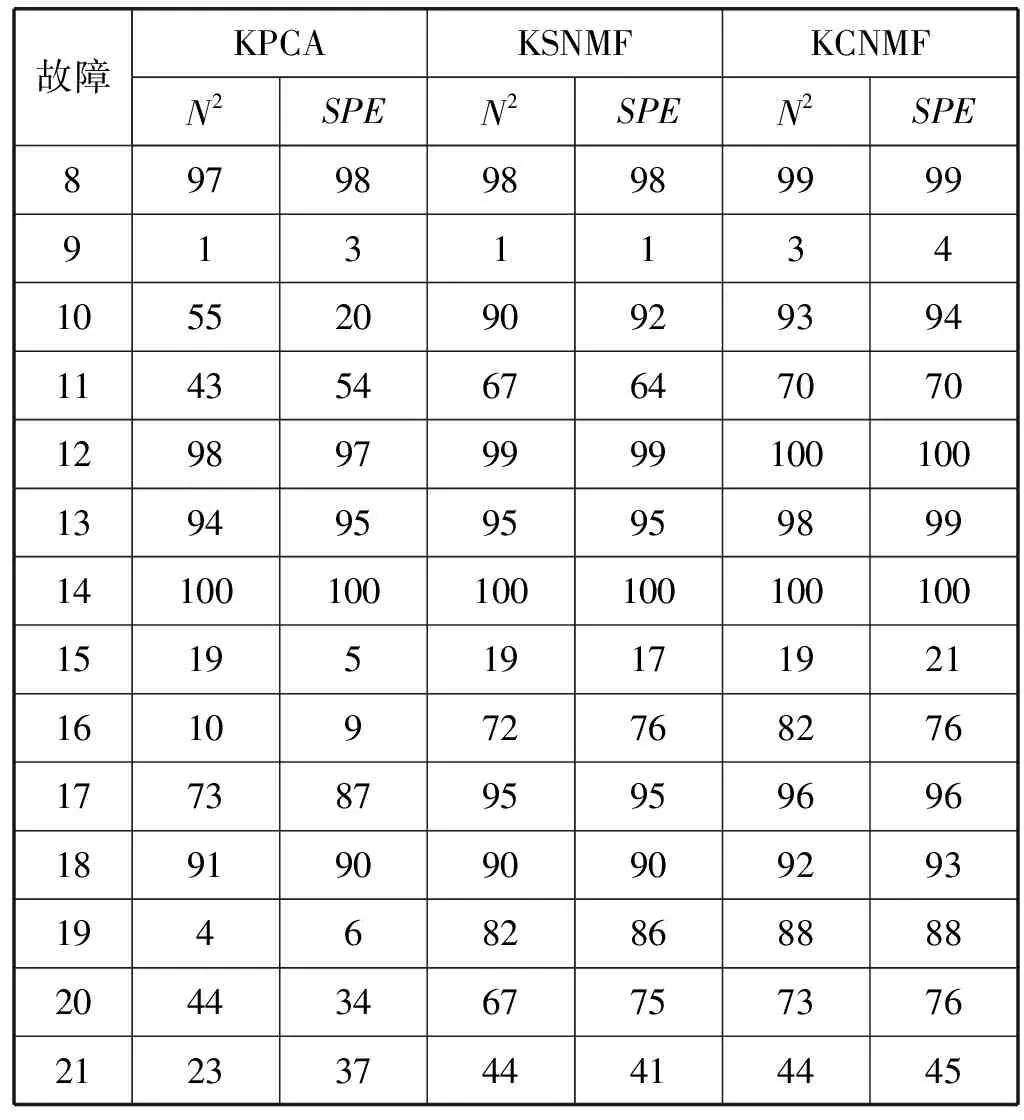
式中:W∈Rm×p表示基矩陣;H∈Rn×p稱作系數矩陣;E∈Rm×n表示殘差;參數p為近似描述分解之后的低維空間的維度。一般地,p NMF方法的求解是一個NP(Non-Deterministic Polynomial)問題,現有的方法都是將其歸結為一個約束優化問題。最基本的優化函數為Lee等[13]提出的基于歐氏距離(F-范數)和廣義Kullback-Leibler散度的優化模型。本文使用歐氏距離來度量矩陣V和兩個分解因子W和H分解前后的誤差大小: (13) s.t.W≥0,H≥0 對于W和H的求解遵循乘性更新法則,最終迭代形式如下[13]: (14) (15) 式(14)和式(15)在整個迭代過程中能夠保證目標函數非增。目標函數達到收斂狀態時,W和H便不再發生變化。 NMF算法提取數據局部特征,面對不完整的數據或者遇到局部噪聲過大的情況,也不會對描述其他元素產生較大的影響,具有良好的穩定性和魯棒性。其中,CNMF算法將原始的NMF算法從一個非凸問題改成凸問題,避免求解優化函數時得到局部最小值。不同于傳統的NMF算法,CNMF并不需要損失部分數據信息。在凸非負矩陣分解算法中對基矩陣進行約束,使得基矩陣的列向量是某些原始數據點的加權求和,W表示有意義的“集群中心體”,具體表現形式為: (16) 則得到: V=WHT+E=VGHT+E (17) 凸包非負矩陣(Convex-Hull NMF,CHNMF)是CNMF框架中的一種,將CNMF的基矩陣W限制為凸包頂點集合Y。首先,CHNMF的局部特征由數據云團凸包頂點構成,頂點數總是少于數據集中數據的總個數,適用于大型數據集的分解。其次,很多研究中選取樣本數據聚類中心為局部特征,聚類中心作為聚類樣本均值往往代表著某類樣本的一般屬性。當正常樣本與故障樣本基本屬性差別較大、中心位置距離較遠時,聚類中心可作為檢測的主要依據;反之,中心數據點作為局部特征具有較低的區分度,就需要獲取更多的數據信息。CHNMF選取數據集流形結構的極端點(凸包頂點)作為局部特征,將聚類中心之外的邊緣數據中蘊含的有效信息也考慮進去,進一步捕捉樣本邊緣特征,比較完整的系統信息有助于提高故障檢測的準確率。最后,因為無須考慮聚類中心位置,CHNMF中W初始值設定不會對最終結果產生較大的影響。 令Y=VG,Y∈Rm×k表示V的凸包頂點的集合。通過在凸包上找到k個合適的數據點來求解下面優化函數的最小值: (18) s.t.yi∈v(V)i=1,2,…,k 若數據集過大,則凸包計算變得困難。對數據進行二次降維,用數據低維映射后的凸包頂點來代替原空間中的凸包頂點[8]。實質上,V中包含有限多的點在空間中形成一個多面體,由下面多面體定理可以得知,數據線性低維投影的凸包上的任何數據點也位于原始數據的凸包上。 多面體定理:在仿射映射π:x→Mx+t下的多面體P的每一幅圖像都是多面體[14]。 FastMap映射[15]可以將樣本矩陣線性投影到二維空間中得到新的樣本矩陣S∈Rm×r,在二維空間中我們選擇其中k個凸包頂點得到基矩陣Y。凸包頂點是特征數據點,而每一個特征數據點是所有數據點的一個凸組合,所以離特征數據點距離越近的點對特征點構成的影響就越大,對應著參數矩陣G∈Rr×k中的數值就會越大[16]。 V=YHT+E≈SGHT+E (19) 式中:H∈Rn×k為系數矩陣。 優化算法的目標函數是: (20) s.t.G≥0,H≥0 迭代更新規則如下[9]: (21) (22) 式中:S是由數據V進行FastMap投影后的數據集合。(STV)+=(|STV|+STV)/2,(STV)-=(|STV|-STV)/2,(STS)+=(|STS|+STS)/2,(STS)-=(|STS|-STS)/2分別表示數據矩陣的正數部分和負數部分。 將數據矩陣中的xi看作是圖中的一個頂點,用G=(V,E)表示圖,V={v1,v2,…,vn}是圖的頂點集合,E={e1,e2,…,em}表示圖中邊的集合[17]。而兩點之間的權重wij構成圖的帶權鄰接矩陣W=(wij),i,j=1,2,…,n,由于G是無向圖,令wij=wji。其中頂點vi∈V的度可以定義為:di=∑wij,度矩陣D是對角元素分別為度d1,d2,…,dn組成的對角矩陣。圖的構建有幾種不同的形式,本文選擇全連通圖的構建形式,頂點vi和vj之間的邊的權重值由高斯相似度函數來計算得到: (23) 式中:參數σ控制相鄰關系的寬度。由式(23)可知:當兩數據點之間具有較近的物理距離時,二者之間的相似度較大,邊的權重值越大;反之,權重值越小。圖拉普拉斯矩陣L=D-W可用于表示包含度和邊的權重值等必要元素的圖。 數據映射之后,在新的基底下的數據表示形式為fk(xi)=hik。此時,數據點之間的近似程度計算如下[11]: (24) 由式(24)可以看出,原來距離較近的兩個數據點在新的基底下同樣能夠保持較近的距離和較大的相似度。 本節提出一種基于核凸非負矩陣分解算法(KCNMF)的故障檢測方法,主要用于解決非線性數據降維和樣本矩陣局部特征提取的問題。 非負觀測數據矩陣V∈Rm×n,其中行向量表示樣本變量,列向量表示每個變量所包含的樣本。對樣本矩陣X進行白化處理得到KPCA空間中的樣本矩陣Z,對Z進行CHNMF分解得到KCNMF模型的表達式如下: Z=SGHT+E (25) 式中:Z∈Rq×n為白化后的樣本矩陣;S∈Rq×r為FastMap映射降維后的樣本矩陣;G∈Rr×k為參數矩陣;H∈Rn×k表示系數矩陣;E∈Rq×n表示殘差矩陣。 采用歐氏距離用于度量矩陣分解前后的近似程度,目標函數優化過程中增加流形正則化約束。非負矩陣分解算法希望提取出的基矩陣能夠更好地近似于原數據矩陣。如果基向量能夠反映數據本身固有的黎曼結構而不是歐幾里得結構,數據的關鍵信息就可以通過幾何結構的局部不變性得以保留下來。如果兩個數據點zi和zj在數據分布的固有幾何形狀上相近,那么新的基底下的數據hi和hj也應該是相接近的[18]。結合式(24)和式(25)得到目標函數具體形式如下所示: (26) 式中:λ是常系數。 保持H不變,按下式更新G+: (27) 保持G不變,按下式更新H+: (28) N2=hTh=zT(SG)(SG)Tz=zTSGGTSTz (29) 而SPE統計量主要用來反映樣本在殘差空間中的投影變化,它表明數據樣本與核凸非負矩陣分解模型的偏離程度,用偏差設定檢測閾值也是一種重要的方法。 (30) 確定N2和SPE統計量之后,還需進一步求得監測統計量的控制限來判定樣本是否處于故障狀態。實際采樣數據大多具有非高斯的特點,所以N2和SPE統計量的控制限就不能通過特定分布方法來確定,否則會造成較大的偏差。作為一種非參數估計方法,核密度估計法(KDE)[19]可用來估計過程數據的概率密度并提取數據分布信息,且不需要已知數據的先驗知識和數據分布。具體形式如下: (31) 最后累積分布函數(CDF)用于計算N2和SPE統計量的控制限。 (32) 由此,在對測試數據進行狀態分析時,如果新數據統計量處于控制限范圍內可判定其屬于正常狀態,如果高于控制限則為故障狀態。 實際工業生產過程是一個非線性系統,但是在某個工作點采樣得到的過程數據可以近似成線性樣本,假設生產過程是擬平穩過程。利用正常操作下的歷史數據構建離線模型得到N2和SPE的故障檢測閾值,新采樣得到的在線數據根據在線檢測流程計算得到新的N2和SPE統計量,用于判斷是否在控制限范圍之內從而說明數據是否故障。則故障檢測過程如下所示: 1) 離線建模階段過程如下: (1) 工業生產的正常操作之下采集傳感器中的數據樣本V∈Rm×n,利用一般的標準化方法對數據進行標準化處理; (4) 利用式(10)求得白化矩陣P,并用式(11)將樣本矩陣進行白化求取新的樣本數據Z; (5) 對白化后的新數據樣本矩陣Z進行凸包非負矩陣分解,求得X和H; 2) 在線建模階段過程如下: (1) 在線數據測試時需先獲取新樣本vnew∈Rm,因為是工業生產是擬平穩過程,使用訓練樣本的均值和方差對此新樣本進行標準化操作; (3) 利用式(11)對vnew求特征空間白化后的樣本znew; (4) 對白化后的新數據樣本矩陣Z進行凸包非負矩陣分解,求得新的系數矩陣hnew; 本文中采用的實驗數據來自于Tennessee Eastman(TE)仿真平臺。TE過程的流程圖如圖1所示。 圖1 TE過程的工作流程圖 整個TE生產過程中,可采得含有52個變量的數據集。數據集可分為22個測試集和22個訓練集。第0號測試數據集和訓練數據集分別表示數據是在生產機器在正常狀態下運行48小時和25小時采集到的,得到的樣本數分別為960個和500個。第1-21號數據集是在21個不同故障模式下經過48小時運行仿真得到,在運行過程的第8個小時處分別引入不同類型的故障,每個數據集都采集960個樣本,從160個樣本之后都為故障樣本。21個故障模式如表1所示。 表1 TE過程故障模式 續表1 對1-21種故障數據集進行檢測時,其難易程度大致可分類如下[20]:檢測較容易的有故障IDV(1-2)、IDV(4-8)、IDV(12-14)和IDV(17-18)。不太容易被檢測的有IDV(10-11)、IDV(16)、IDV(19)和IDV(20-21)。非常難以被檢測到的有IDV(3)、IDV(9)和IDV(15)。 選取相對比較有代表性的故障4、故障10和故障19作為實驗對象來測試核凸非負矩陣分解算法的故障檢測性能,以驗證KCNMF對數據非線性的處理以及對局部特征的挖掘是有否有利于提高檢測準確率。圖2-圖5分別是PCA、KPCA[21]、CHNMF和KCNMF四種方法對TE過程故障4的故障檢測的結果。 圖2 PCA方法的故障4檢測結果 圖3 KPCA方法的故障4檢測結果 圖4 CHNMF方法的故障4檢測結果 圖5 KCNMF方法的故障4檢測結果 從仿真結果可以看出,KPCA的檢測結果優于線性檢測算法PCA,說明KPCA對于非線性故障數據的處理具有較好的效果。而KCNMF的檢測準確率又優于KPCA。因為故障4是由反應器冷卻水入口溫度產生改變而造成流速和反應器中溫度兩個局部變量變化造成的,其他變量基本保持穩定,KCNMF方法可以很好地提取數據中的局部信息,提高了工業過程的故障檢測性能。另外,KCNMF方法可以很好地應對數據中的非線性關系,所以檢測效果比CHNMF方法更好。 故障10是物料C的溫度發生了改變,但由于TE過程可以反饋這個變化,并且緩慢地消除了這個誤差,使系統的溫度盡可能調整到正常值。圖6-圖9分別為PCA、KPCA、CHNMF、KCNMF對故障10的檢測結果。可以看出PCA和KPCA的N2和SPE統計量只能夠檢測出部分故障就是故障10的特點造成的。而CHNMF的檢測結果優于上面兩種方法,對于局部特征關注優勢明顯。不過,KCNMF方法的N2和SPE統計量還是比上述三種方法更勝一籌。 圖6 PCA方法的故障10檢測結果 圖7 KPCA方法的故障10檢測結果 圖8 CHNMF方法的故障10檢測結果 圖9 KCNMF方法的故障10檢測結果 圖10-圖13分別為PCA、KPCA、CHNMF和KCNMF方法對故障19的檢測結果。通過表1可知,雖然故障19的故障類型未知,但根據檢測結果可以推測出,故障19可能與局部變量發生變化有關。可以看出PCA、KPCA以及CHNMF算法的檢測準確率普遍較低,而KCNMF方法因在數據非線性關系的處理以及局部特征的提取利用上面具有較大的優勢,因此能夠表現出較高的檢測準確率。 圖10 PCA方法的故障19檢測結果 圖11 KPCA方法的故障19檢測結果 圖12 CHNMF方法的故障19檢測結果 圖13 KCNMF方法的故障19檢測結果 表2中列出了對1-21種TE過程非線性數據分別使用三種故障檢測方法的檢測準確率。其中核半非負矩陣分解算法(KSNMF)[22]提取的局部特征是數據云團的聚類中心。表中結果比較可得,KSNMF和KCNMF這兩種方法的檢測都明顯優于KPCA,這說明對于數據云團局部信息的提取利用有助于故障數據的識別與檢測。而KCNMF方法相較于KSNMF方法檢測中結果表現更好,因為KCNMF將偏離聚類中心的數據信息也考慮進去,當不同樣本聚類中心過于接近,以此為基礎的局部特征不具備良好的區分度,則邊緣數據所含信息對檢測會起到重要作用。對分解結果產生很大影響。KCNMF不再需要設置聚類中心的初始值,避免了迭代初始值和低維階次設定不準確導致檢測結果存在誤差的情況出現。總體來說,KCNMF對第一、二類故障數據整體檢測效果較好,而第三類故障檢測效果不佳,還需進一步研究。 表2 KPCA、KSNMF和KCNMF方法故障檢測率比較 (%) 續表2 為解決高維非線性數據降維問題,并求取更有意義的樣本矩陣局部特征,本文提出了核凸非負矩陣分解算法。首先對數據集進行核主元分析并對特征向量進行縮放求得白化矩陣,利用白化矩陣對樣本方差進行縮小或放大操作。接下來,對白化后的樣本矩陣進行凸包非負矩陣分解。用凸包頂點作為局部特征所求得的故障檢測方法在關注數據集聚類中心之外,還充分利用了邊緣數據信息,能捕捉到其他方法捕捉不到的特征。流行正則化約束項又能保證分解過程中樣本矩陣的本質不發生改變,這些算法的結合使得故障檢測更加準確。本文利用TE過程數據集對KCNMF方法進行仿真驗證,取得了較好的診斷結果,并驗證了所提方法的有效性。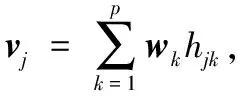
2.2 凸包非負矩陣分解算法
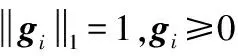

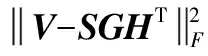
2.3 圖的基本理論

3 核凸非負矩陣分解的故障檢測方法
3.1 在KPCA空間進行凸包非負矩陣分解
3.2 故障檢測統計量


3.3 基于核凸非負矩陣分解算法的故障檢測過程
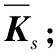
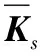
4 仿真分析
4.1 實驗數據



4.2 實驗結果







5 結 語

