鐵路抗震規范地震力簡化算法適用性研究

楊智慧

中國鐵路設計集團有限公司，天津 300308

經過十幾年大規模高速鐵路建設，我國已經建成四通八達、南北貫通的高速鐵路網絡［1］。我國高速鐵路的特點是橋梁結構占比高，整體橋梁結構占線路總長超過50%，某些線路達70%以上［2］。我國是一個多地震國家，大中型地震引起的橋梁震害十分嚴重［3-5］。為保證高烈度地震區高速鐵路運營安全，有必要開展鐵路橋梁結構抗震計算研究。

橋梁結構地震響應機制復雜，地震力計算一般通過建立有限元模型來完成。我國高速鐵路橋梁結構無論是簡支梁還是一般連續梁結構均已形成成熟的標準跨度通用圖體系，并廣泛應用于實際工程。多遇地震下常規橋梁結構一般使用現行GB 50111—2006《鐵路工程抗震設計規范》（2009年版）中規定的簡化算法計算橋墩地震力。因地震荷載工況有時會控制設計，為提高計算科學性和設計質量，有必要研究簡化算法與有限元法計算精度誤差，以及不同設計參數的適用范圍。針對現行震規簡化算法，劉春［7］選取2 座實際工點連續梁橋，分別使用簡化算法和有限元法進行計算對比，由于所選樣本較少，對產生計算差值的原因沒有深入分析。李曉波［7］使用簡支梁橋對比2 種方法在縱橋向和橫橋向地震力的計算結果，但沒有針對設計參數做具體分析。魏詩雅［8］對比分析了簡化算法、反應譜法和彈性時程法在縱橋向和橫橋向地震力計算結果，但只選取一座橋梁工點，代表性不足。

本文通過建立不同設計參數的多組計算模型，分析簡化算法與有限元法的差異，以及計算誤差產生的原因，研究不同設計參數下簡化算法的計算精度和適用性，為鐵路橋梁抗震設計計算提供依據。

1 簡化算法和有限元法計算原理

1.1 簡化算法計算原理

GB 50111—2006 附錄E 給出了梁式橋多遇地震下橋墩抗震計算簡化方法，雖然規范7.2.5 條指出該方法適用于簡支梁橋墩地震力計算，但實際設計中為提高效率，也將該方法應用于一般常規連續梁橋地震響應計算中。

簡化算法基本原理是將上部結構影響簡化為作用于墩頂的質點建立單質點-單墩模型（圖1），地震動輸入采用反應譜函數，將模型一階振型地震響應作為橋墩地震力計算結果。圖中，mb為質點質量，mi和hi分別為墩身i段質量和距承臺頂高度，H和hf分別為墩身高度和承臺厚度，δ22處為基礎約束柔度值。

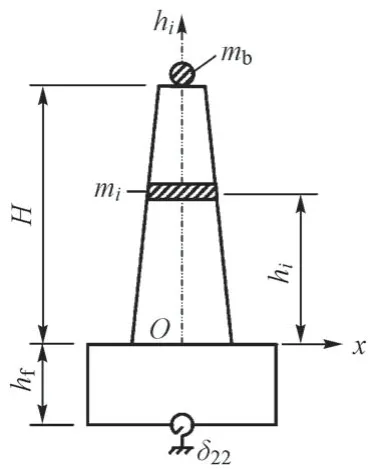
圖1 簡化算法計算模型

橋墩基礎頂面剪力V0和彎矩M0計算式分別為

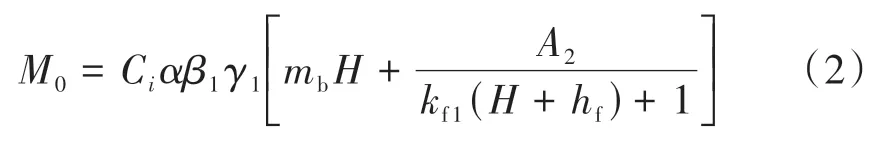
式中：Ci為橋梁重要性系數；α為水平地震基本加速度；Cq為剪力振型耦合系數；β1為第一振型動力放大系數；γ1為第一振型的振型參與系數；kf1為第一振型基礎質心角變位的振型函數；A1、A2均為計算系數。

1.2 有限元建模

采用MIDAS/Civil 軟件建立有限元模型。橋墩和承臺使用空間梁單元模擬，墩頂質點與墩頂節點之間使用剛性連接。基礎約束采用6×6 一般彈性支承剛度矩陣，地震動輸入采用反應譜函數。

2 簡化算法與有限元法縱向地震力計算對比

2.1 單墩模型計算對比

為排除墩頂質點和承臺的影響，建立無墩頂質點和承臺的簡化單墩模型。為保持建模方式一致，有限元模型墩底約束除計算方向轉動剛度外，其他方向均輸入一個較大值來模擬固結。

為研究截面類型的影響，以實際工程中常規鐵路連續梁結構為基礎建立圓端形、圓形和矩形3 種截面類型橋墩，截面尺寸見表1。

表1 3種墩形截面尺寸

分別建立多組不同墩高的計算模型，其中圓端形墩高變化范圍為3.0 ～35.0 m、圓形墩高變化范圍為2.0 ～ 40.0 m、矩形墩高變化范圍為2.5 ～ 40.5 m，基本涵蓋實際工程墩高區間。研究簡化算法與有限元法比值隨墩高的變化規律，見圖2。可知，采用2 種方法計算不同墩形墩底剪力和彎矩變化規律基本一致。其中墩底剪力比值隨墩高增加而線性增大；墩底彎矩比值最初隨墩高增加而線性增大，墩高達到一定值后基本不變。

圖2 不同墩高下簡化算法與有限元法結果對比

針對常規鐵路連續梁橋墩，以2 種方法結果相對差值±10%作為可接受的精度范圍，簡化算法對不同類型橋墩墩高適用范圍分別是12.0 ～26.0 m（圓端形橋墩）、16.0 ～ 28.0 m（圓形橋墩）和15.5 ～ 26.5 m（矩形橋墩）。3 種截面類型墩高適用范圍基本一致，說明截面類型對簡化算法計算精度影響不大。

2.2 考慮承臺的單墩模型計算對比

簡化算法計算模型中對于承臺只考慮了厚度hf和重量mf兩個參數，其中參數mf在一階振型參與系數γ1計算中體現。有限元模型中承臺和墩身均采用空間梁單元模擬。因承臺截面尺寸遠大于墩身，厚度較大時承臺質量占橋墩總質量比例大，地震響應不容忽視。因此，分別討論承臺厚度和承臺尺寸兩個參數對計算結果的影響。

以墩高16 m 圓端形橋墩為基礎，墩底增加承臺部分，截面縱橋向和橫橋向尺寸分別為9.4、16.4 m，改變承臺厚度建立多組計算模型計算縱橋向地震響應。不同承臺厚度下簡化算法與有限元法結果對比見圖3。

圖3 不同承臺厚度下簡化算法與有限元法結果對比

由圖3 可知，承臺厚度較小時2 種方法計算結果很接近，隨著厚度增大，二者比值逐漸減小，承臺底彎矩和剪力均呈線性變化，簡化算法結果偏小。承臺厚度大于2.0 m 時2 種方法彎矩差值超過20%。原因是承臺厚度3.0 m 時有限元模型的高階振型參與系數明顯大于承臺厚度0.1 m 時有限元模型的高階振型參與系數，此時高階振型影響不可忽略。而簡化算法只考慮一階振型，導致計算結果偏小。

以承臺厚度1 m 模型為基礎，改變截面尺寸建立多組模型計算縱橋向地震力，承臺截面尺寸見表2，簡化算法與有限元法結果比值見圖4。可知，承臺截面尺寸對2 種方法地震響應結果影響很小，說明承臺厚度是影響簡化算法計算精度的主要因素。

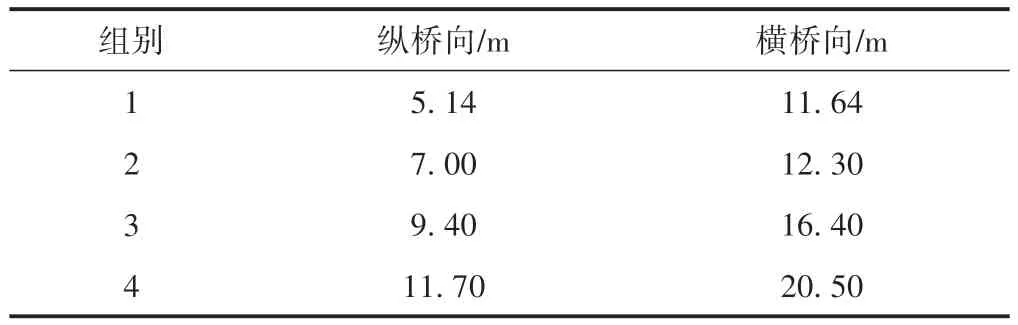
表2 承臺截面尺寸

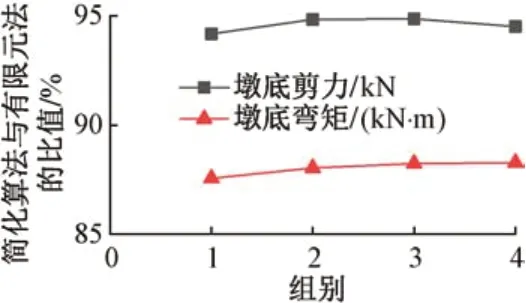
圖4 不同承臺截面尺寸下簡化算法與有限元法結果對比

2.3 考慮墩頂質量的模型計算對比

簡化算法將上部結構簡化為位于墩頂的一個質點，將梁部重量、活載、二期恒載等的地震效應簡化為質點質量一個參數來表征。計算模型中質點位于墩頂，可以看作墩頂附加質量。

GB 50111—2006 對于地震力計算中上部結構不同荷載作用位置均有明確規定：梁體地震作用縱橋向位于支座中心處、橫橋向位于梁高的1/2 處；活載地震作用位置位于軌頂以上2 m 處。簡化算法中質點只能位于墩頂，無法改變位置，造成設計中上述規定無法執行。

為研究質點高度對地震響應的影響，以圓端形橋墩為基礎，建立單質點-單墩模型，改變質點高度建立多組有限元模型計算縱橋向地震響應，見圖5。可知，隨著質點高度的增加，墩底彎矩和剪力均逐漸減小，基本呈線性變化。原因是有限元模型縱橋向一階振型周期隨質點高度增大而增大，且均位于反應譜函數下降段，導致整體地震響應快速下降。

圖5 縱橋向地震響應有限元計算值

2.4 考慮跨度的模型計算對比

對于不同跨度的簡支梁橋和連續梁橋，使用有限元法計算地震響應時須建立不同數值模型。對于簡化算法，橋梁跨度不同只會影響墩頂質點mb的取值。

連續梁橋只有固定墩支座施加縱橋向約束，因此設計中認為由固定墩承擔連續梁全梁地震力。若使用簡化算法計算固定墩縱向地震響應。

為研究將連續梁全梁重量簡化為單一質量這種建模方式的合理性，選取（80 + 128 + 80）m 連續梁橋建立全橋有限元數值模型和固定墩單墩有限元數值模型，其中單墩模型連續梁梁重以質點形式施加于墩頂，用來代表簡化算法的建模方式。2 個模型縱橋向地震響應結果見表3。可知，單墩模型與全橋模型剪力和彎矩結果比值分別為128.16%和127.45%，無論是剪力還是彎矩，單墩模型計算結果均偏大。

表3 固定墩縱橋向地震力結果對比

為研究產生差異的原因，查看全橋模型自振振型發現，縱橋向一階振型中上部結構發生較大變形［圖6（a）］修改梁部材料彈性模量提高梁部剛度后，全橋模型縱橋向一階振型見圖6（b），此時自振振型中梁部幾乎無變形。對比此時全橋模型與單墩模型縱橋向地震力計算結果，發現相對差值不足2%。因此，連續梁跨度較大時，振動中因梁部自身變形引起的能量耗散不容忽視。簡化算法使用全梁重量作為固定墩頂質點質量的建模方式會導致地震響應計算結果偏大。

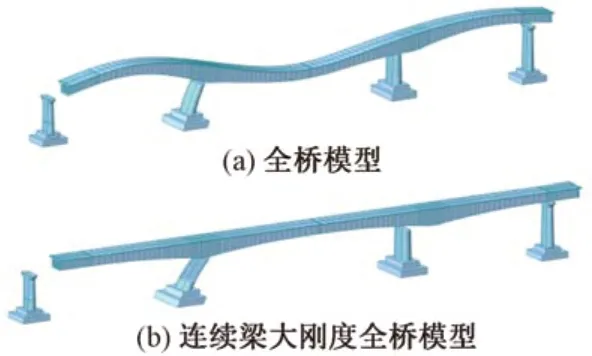
圖6 縱橋向一階振型

3 簡化算法橫向地震力計算合理性研究

使用簡化算法計算橫橋向地震響應時，建模方式與縱橋向類似。墩頂質點質量一般由墩頂支座反力確定：簡支梁橋結構規則，約束方式統一，支座反力取一跨簡支梁梁重；連續梁橋需通過建立全橋模型計算確定各橋墩支座反力。

以上處理方式隱含了2 個前提條件：①所有梁部重量均會產生水平地震力；②梁部地震力在各橋墩之間的分配比例與支座反力成正比。

關于第一個前提條件，選取（40+64+40）m 連續梁橋建立全橋有限元模型，改變連續梁材料彈性模量來模擬連續梁剛度變化，初始彈性模量為3.550 ×107kN/m2，建立多組模型計算各橋墩墩頂地震剪力之和，結果見表4。可知，不同連續梁剛度下上部結構水平地震力并不相同，彈性模量變化引起墩梁剛度比變化，導致結構自振特性改變。

表4 不同連續梁剛度墩頂剪力對比

橫橋向一階振型見圖7。可知，梁部并非剛體，振動中會發生變形，導致部分能量耗散。因此，并非所有梁部重量均會產生水平地震力，說明第一個前提條件并不合理。只有當梁部剛度很大（對應墩梁剛度比也很大）時，梁部變形很小，能量耗散才可忽略，墩頂地震剪力之和趨于穩定。

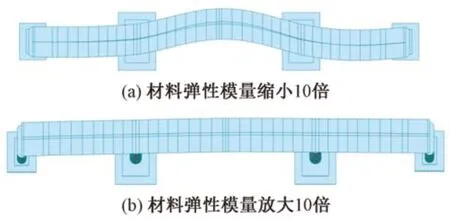
圖7 橫橋向一階振型

關于第二個前提條件，提取不同連續梁剛度下各橋墩墩頂地震剪力與所有橋墩墩頂地震剪力之和的比值，見圖8。可知，各橋墩墩頂水平地震力占比隨著連續梁剛度變化而變化，但連續梁剛度變化并不會改變各橋墩支座反力，說明第二個前提條件也不合理。梁部地震力在各橋墩之間的分配比例并不與支座反力成正比，而是受墩梁剛度比的影響。

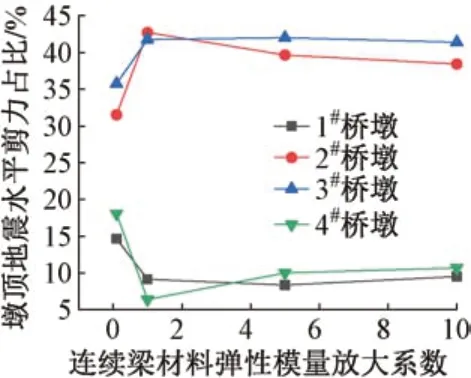
圖8 不同連續梁剛度各橋墩墩頂水平地震力占比

綜上，使用單質點-單墩模型無法準確反映連續梁結構橫橋向振動特性，簡化算法無法考慮墩梁剛度比，但墩梁剛度比參數對梁部地震響應和梁部地震力在各橋墩之間的分配比例均會有影響。除材料彈性模量外，截面形式、墩高、跨度等參數變化也會影響結構墩梁剛度比，進而改變結構振動特性，最終反映到橫橋向地震力計算結果中。多個設計參數互相耦合、互相影響，機理復雜，難以通過對單一參數分析獲得準確結論。另外，這種影響機制并非連續梁橋獨有，對跨度較大或墩高較矮的簡支梁橋同樣適用。因此，不建議使用簡化算法計算連續梁橋橫向地震力。

4 結論

1）簡化算法對簡化單墩模型計算精度較高，不同類型橋墩墩高適用范圍分別是12.0 ～26.0 m（圓端形橋墩）、16.0 ～28.0 m（圓形橋墩）和15.5 ～ 26.5 m（矩形橋墩）。

2）采用簡化算法計算縱橋向地震力，承臺厚度較大時計算結果偏小；跨度較大時使用全梁重量作為固定墩頂質點質量會導致計算結果偏大。

3）簡化算法計算模型不能準確反映橫橋向橋梁結構振動特性和設計參數對地震響應的影響，不建議使用該方法進行橫向地震力計算。